基于變尺度黑洞和種群遷徙的粒子群優化算法

許文俊,王錫淮

(上海海事大學物流工程學院,上海 201306)

1 引言

粒子群優化PSO(Particle Swarm Optimization)算法是Kennedy等[1,2]于1995年提出的一種生物啟發式算法。PSO模擬鳥群和魚群的覓食行為,通過群體中個體的自身認知和個體之間的信息交流來實現在解空間內的尋優操作。PSO具有收斂性好、結構簡單、需要設置的參數少等優點,一經提出就得到了國內外研究人員的關注,現已在微電網運行優化[3]、圖像處理[4]、神經網絡[5]和調度問題[6]等領域得到了廣泛的應用。但是,PSO在應用中也暴露出不少缺點,如:容易陷入局部最優、收斂速度慢、搜索精度不高和魯棒性較差等[7]。針對PSO的不足,國內外研究人員進行了大量研究,對PSO進行了諸多改進與優化。Zhang等[8]針對PSO收斂速度慢的問題,提出基于黑洞機制的PSO——RBHPSO(Random Black Hole Particle Swarm Optimization)算法,通過黑洞的吸引使粒子快速到達全局最優附近,增強了算法的全局探索能力。蔣麗等[9]為了提高PSO的群體多樣性、改善算法易陷入局部最優等缺陷,在二階振蕩PSO的振蕩環節采用互不相同的參數取值來調節PSO的全局和局部搜索能力,進一步提高算法的尋優能力。胡錦帆等[10]提出了基于單純形搜索的PSO,通過自適應策略確定PSO的慣性權重,同時利用單純形搜索來引導粒子的搜索方向,提高了PSO的收斂速度和求解精度。Mahfouf等[11]在PSO中引入了自適應慣性權重和加速因子,增強了PSO的全局搜索能力,同時為算法跳出局部最優提供了有效的機制。Du等[12]針對PSO收斂速度慢、易陷入局部最優的問題,提出了一種基于Levy飛行機制的改進自適應粒子群優化算法,通過Levy飛行的跳躍幫助算法逃離局部最優,增強了PSO的收斂速度與收斂精度。

為了克服PSO收斂速度慢、易早熟收斂的問題,本文提出了基于變尺度黑洞和種群遷徙的PSO——IRBHPSO(Improved Random Black Hole Particle Swarm Optimization)算法。其思路是引入變尺度黑洞來平衡全局探索和局部尋優的權重;引入基于混合策略的位移系數,增強算法在迭代前期的收斂速度和迭代后期的局部尋優能力;把基于種群遷徙的蝴蝶優化算法BOA (Butterfly Optimization Algorithm)[13]作為局部算子融入PSO中,改善了PSO收斂速度慢、易陷入局部最優的問題。基于12個基準測試函數進行仿真實驗以及Wilcoxon秩和檢驗。實驗結果表明,本文所提IRBHPSO改善了PSO收斂速度慢、易早熟收斂的問題,增強了PSO的全局探索能力和局部尋優能力,驗證了IRBHPSO的優越性和本文所提改進策略的有效性。

2 粒子群優化算法

2.1 基本粒子群優化算法

PSO采用的是速度-位置搜索模型,PSO忽略掉粒子的質量與體積,按照一定速度飛行,根據自身經驗與群體經驗更新速度與位置[14]。在每次迭代過程中,粒子都會向著2個最優粒子移動,一個是粒子本身在迭代過程中搜尋到的最優點,即個體最優pbest,另一個是所有粒子在迭代過程中搜尋到的最優點,即全局最優gbest。所有粒子的速度和位置分別按照式(1)和式(2)更新:

v(t+1)=

ωv(t)+c1r1(pbest-x(t))+c2r2(gbest-x(t))

(1)

x(t+1)=x(t)+v(t+1)

(2)

其中,v(t)和v(t+1)分別為粒子在第t次和第t+1次迭代時的速度;x(t)和x(t+1)分別為粒子在第t次和第t+1次迭代時的位置;pbest為粒子的個體最優位置;gbest為粒子的全局最優位置;ω為慣性權重;c1和c2為學習因子;r1和r2為[0,1]的隨機數。

2.2 黑洞機制

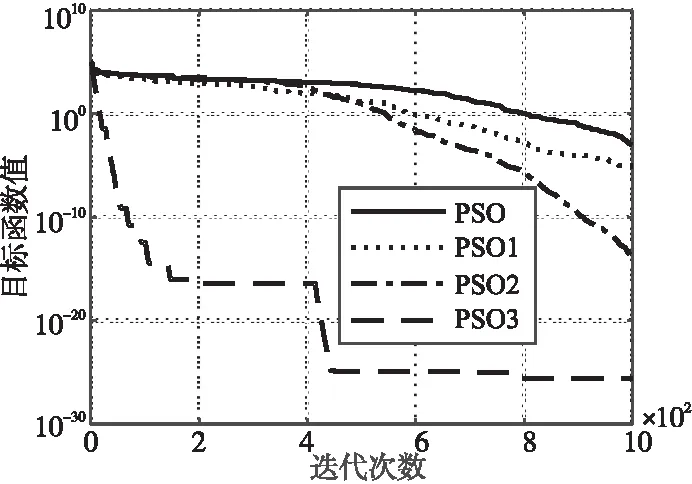
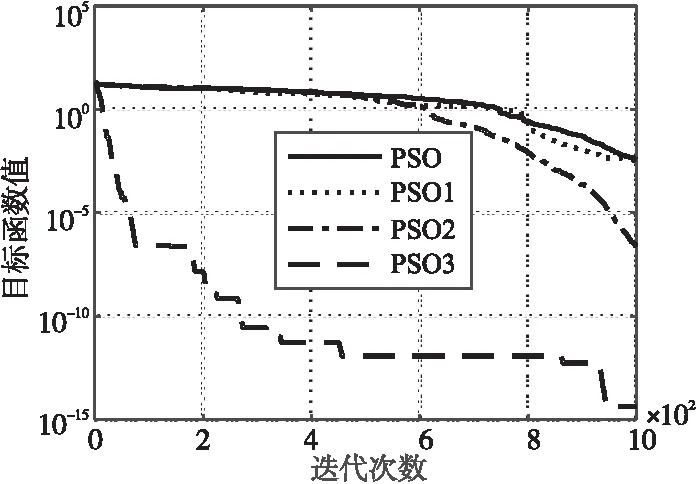
黑洞機制保留原位置更新策略,同時引入一種新的位置更新策略,通過黑洞吸引概率P在2種位置更新策略中選擇。新的位置更新策略在以全局最優gbest為球心、R為半徑的區域內設定一個假想黑洞,以黑洞吸引概率P表示黑洞對粒子吸引的能力。對于[0,1]的隨機數L,如果L

(3)

其中,gbest為全局最優,R為黑洞的半徑,L和r3為[0,1]的隨機數,P為黑洞吸引概率。

3 改進粒子群優化算法

3.1 變尺度黑洞

黑洞機制通過假想黑洞的吸引使得粒子快速移動至全局最優附近,從而實現算法的快速尋優。黑洞機制增強了算法的全局探索能力,但該策略會使粒子過早到達全局最優附近,增加粒子陷入局部最優的可能性。RBHPSO雖然提高了PSO的收斂速度,但是并未改善PSO易早熟收斂的問題。綜上,本文提出變尺度黑洞來平衡全局探索和局部尋優的權重,變尺度黑洞具體實現如式(4)所示:

(4)

其中,Rstart和Rend分別為變尺度黑洞半徑Rc的迭代初始值和迭代最終值;t為當前迭代次數;T為算法最大迭代次數。

變尺度黑洞機制對黑洞半徑進行改進,使其可以隨著迭代次數的增加而線性減小。變尺度黑洞保留了黑洞機制較強的全局探索能力,同時平衡了算法的全局探索和局部尋優的權重。在迭代前期,粒子被黑洞吸引后,移動至當前全局最優附近。由于當前黑洞半徑較大,則粒子距離當前全局最優較遠,算法陷入局部最優的可能性較低;在迭代后期,當粒子被黑洞吸引,粒子移動至全局最優附近。由于此時黑洞半徑較小,并且當前全局最優已經非常接近理論最優,粒子可以在局部區域內仔細尋優,算法的局部尋優能力得到改善。

3.2 基于混合策略的位移系數

在PSO的位置更新策略中,粒子位置的系數始終為1。固定的位移系數使得在迭代前期,粒子無法以較大的位移進行全局搜索,無法快速收斂;在迭代后期,粒子已經移動至全局最優附近,此時粒子又以較大的步長在全局最優附近大幅度移動,易錯過全局最優值。位移系數始終為1會導致算法過度信賴已有解,同時削弱了算法潛在的全局尋優能力,放大了PSO局部尋優能力弱的缺點。基于上述分析,本文提出一種基于線性遞減和混沌映射的位移系數β,簡稱基于混合策略的位移系數,基于混合策略的位移系數具體實現如式(5)～式(9)所示:

β=β1+β2

(5)

(6)

(7)

(8)

x(t+1)=β·x(t)+v(t+1)

(9)

其中,β1為線性遞減的位移系數,β1s為β1的迭代初始值,β1e為β1的迭代最終值,St為正弦混沌映射,β2為基于正弦映射的位移系數,β為基于混合策略的位移系數。

基于混合策略的位移系數β受到線性遞減策略和正弦混沌映射的作用,隨著迭代次數的增加而非線性地減小。在迭代前期,β1較大,β2的比重較小,此時粒子的位移系數大于1,粒子在解空間內快速尋優,較大的步長可以加速粒子移動至全局最優附近,增強算法的收斂能力;在迭代后期,β1較小,β2的比重增大,此時粒子的位移系數較小,且在一定范圍內混沌地變化。粒子以較小的位移在局部范圍內仔細尋優,提高算法的收斂精度。并且若粒子陷入局部最優,在β2的作用下,粒子可以借助變化的位移逃離局部最優,有效增強了算法的局部尋優能力。

3.3 種群遷徙的BOA

蝴蝶優化算法BOA是Arora等[13]于2019年提出的啟發式優化算法。BOA是受到自然界中蝴蝶通過自身的感知器官分辨食物的位置的啟發而提出的。BOA參數少、原理簡單、易于實現。在研究中發現,BOA的收斂速度和尋優精度要明顯優于PSO[15]的。

BOA中的蝴蝶個體強調個體本身的搜索,降低了由于精英個體的錯誤引導而導致群體陷入局部最優的可能性。但是,BOA缺乏有效的加速收斂機制,導致其收斂速度依然較慢。為了改善PSO收斂速度慢、易陷入局部最優等問題,本文提出基于種群遷徙的BOA,將其作為局部算子融入PSO的位置更新公式中,改進后的位置更新公式如式(10)～式(13)所示:

x(t+1)=

(10)

f=C·Iγ

(11)

Lt+1=μ·Lt·(1-Lt)

(12)

(13)

其中,rand為[0,1]的隨機數;f為蝴蝶產生的香味;C、I和γ分別為蝴蝶的感覺因子、香味的刺激強度和冪指數;xa(t)和xb(t)分別為隨機生成的第a和第b只蝴蝶在第t次迭代的位置;P1～P3為選擇概率;Lt為logistic映射;μ=4;xp(t+1)為蝴蝶個體經過種群遷徙后的位置。

在基于變尺度黑洞的PSO中加入基于種群遷徙的BOA算子,既保留了變尺度黑洞機制較強的全局尋優能力,又在BOA的作用下強調種群中個體自身的尋優,增強了算法的局部尋優能力,克服了PSO易早熟、易陷入局部最優的缺點。同時,在種群遷徙的作用下,通過全局最優解和更新后的位置引導種群整體向全局最優靠近,增加了算法的收斂速度,為算法提供了一種有效的加速收斂機制,增強了算法的全局收斂能力。

這種基于變尺度黑洞、混合策略的位移系數和以種群遷徙的BOA為局部算子的PSO稱為改進RBHPSO,簡稱IRBHPSO。

3.4 算法步驟

本文提出的IRBHPSO尋優步驟如下所示:

步驟1種群初始化:隨機生成含有N個粒子的種群,對粒子的速度和位置進行初始化。

步驟2根據適應度函數計算出粒子的適應度值,選擇出個體最優和全局最優。

步驟3按照式(8)和式(12)更新正弦映射和logistic映射。

步驟4按照式(4)和式(5)更新變尺度黑洞半徑Rc和基于混合策略的位移系數β。

步驟5粒子按照式(1)和式(10)更新粒子的速度和位置。

步驟6按照式(13)進行種群遷徙。

步驟7更新粒子的適應度值,并重新選擇個體最優和全局最優。

步驟8判斷當前運算是否滿足停止條件,如果滿足,輸出最優結果,終止運算;若不滿足,則跳轉到步驟3繼續運算。

IRBHPSO算法流程圖如圖1所示。

Figure 1 Flow chart of IRBHPSO圖1 IRBHPSO流程圖

3.5 IRBHPSO的時間復雜度分析

設粒子群的規模為N,算法最大迭代次數為T,搜索空間的維度為D,根據IRBHPSO的描述和時間復雜度的運算規則,增加變尺度黑洞的時間復雜度為O(N·D·T);增加基于混合策略的位移系數的時間復雜度為O(N·D·T);增加基于種群遷徙的BOA算子的時間復雜度為O(N·D·T)。所以,IRBHPSO總的時間復雜度為O(N·D·T)。因此,相較于PSO,IRBHPSO的時間復雜度并未增加,沒有增加計算負擔。

4 實驗與結果分析

4.1 實驗設計與基準測試函數

為了驗證本文提出的IRBHPSO的優越性和改進策略的有效性,對12個基準測試函數進行仿真實驗。實驗所用基準測試函數包括4個單模態基準測試函數、4個多模態基準測試函數和4個復合基準測試函數。各個基準測試函數的相關信息如表1所示。

4.2 算法參數設置

本文在Intel?i7-5500 CPU@2.40 GHz, 內存為8.00 GB,Windows 10操作系統和MATLAB 2016a的環境下對文中所提所有算法進行仿真實驗。

本文選取PSO、引力搜索算法GSA (Gravitational Search Algorithm)[16]、RBHPSO、BOA和IRBHPSO進行仿真實驗。為了使實驗結果可信、客觀,設本文所有實驗算法的種群規模N=30,算法最大迭代次數T=1000,算法其他主要參數如表2所示。

4.3 IRBHPSO性能分析

為了驗證IRBHPSO的優越性,本節列出PSO、GSA、RBHPSO、BOA及IRBHPSO在12個基準測試函數上獨立運行30次得到的尋優結果的最優值(best)、最差值(worst)、平均值(mean)和標準差(std),不同算法的尋優結果對比如表3所示。

4.3.1 IRBHPSO收斂精度分析

從表3可知,在f1、f2、f3、f4、f5、f6、f7、f8和f10上,相較于PSO,IRBHPSO的收斂精度高出多個數量級,并且IRBHPSO在f7上直接收斂至理論最優,以上表明IRBHPSO可以有效克服PSO易早熟、易陷入局部最優的缺點;在f11和f12上,IRBHPSO和PSO都收斂至理論最小值附近,兩者收斂精度的數量級相同,表明IRBHPSO和PSO在f11和f12上的收斂能力基本一致。在f9上,IRBHPSO表現較差,PSO的收斂精度高出IRBHPSO的3個數量級,IRBHPSO未能產生較好的優化效果。根據無免費午餐NFL(No-Free-Lunch)[17,18]定理,在有限的搜索空間,對于任意2種算法,它們的期望性能是相同的,也就是說,針對某個具體的優化問題,在該問題上表現好的算法,在其他問題上的表現也可能不盡如人意。基于以上分析,IRBHPSO在大部分函數上的收斂精度均較高,但是在f9上的收斂精度較差,這種現象是可以接受的。綜上所述,本文提出的IRBHPSO可以克服PSO易早熟、易陷入局部最優的缺點,有效提高了PSO的收斂精度。

Table 1 Benchmark test functions表1 基準測試函數

Table 2 Main parameters of each algorithm表2 算法的主要參數

相較于RBHPSO,IRBHPSO表現出了優良的收斂精度。除f9外,IRBHPSO的收斂精度高于RBHPSO的,表明IRBHPSO的收斂精度相較于RBHPSO的得到了提升。對比其他經典尋優算法(GSA和BOA),IRBHPSO依舊表現優異。在f1、f2、f3、f5、f6、f8和f10上,IRBHPSO的收斂精度提升多個數量級。在f4、f11和f12上,IRBHPSO的收斂精度與GSA和BOA的基本持平。在f7上,IRBHPSO的收斂精度高于GSA的,但低于BOA的。IRBHPSO僅在f9上的收斂精度低于GSA和BOA的。

綜上所述,IRBHPSO無論是相較于PSO、改進PSO(RBHPSO)還是其他尋優算法(GSA和BOA),其收斂精度都處于較高水平,表明本文提出的IRBHPSO可以有效克服PSO易早熟、易陷入局部最優的缺點,驗證了IRBHPSO在收斂精度上的優越性。

Table 3 Comparison of optimization results of PSO and related algorithms表3 PSO與相關算法尋優結果對比

4.3.2 IRBHPSO收斂速度分析

由于篇幅限制,同時為了直觀展示不同算法的尋優過程、比較各算法的收斂速度,本節選取5種算法對f1、f2、f3、f4、f6、f7和f10的迭代進化曲線,如圖2～圖8所示。f1～f4為單峰函數,此類函數比較容易達到最優值;f6、f7和f10為多峰函數,此類函數具有較多局部最優,易使算法過早收斂。對于f1～f4,從圖2～圖5可以直觀看出,IRBHPSO的收斂速度遠大于PSO、GSA、RBHPSO和BOA的收斂速度,表明IRBHPSO在面對單峰函數時具有較好的全局收斂能力;對于f6、f7和f10,IRBHPSO依舊表現出了較強的收斂性能。從圖6～圖8可以看出,IRBHPSO的收斂速度快于或約等于其他4種算法的,表明IRBHPSO在面對復雜函數時依然可以進行很有效的全局尋優。

綜上,在單峰函數和多峰函數上,IRBHPSO都表現出了較強的全局探索性能,證明IRBHPSO改善了PSO收斂速度慢的問題,增強了算法的全局探索能力,驗證了IRBHPSO在收斂速度上的優越性。

Figure 2 Iterative evolution curves of PSO and related algorithms on f1圖2 PSO與相關算法對f1的迭代進化曲線

Figure 5 Iterative evolution curves of PSO and related algorithms on f4圖5 PSO與相關算法對f4的迭代進化曲線

Figure 6 Iterative evolution curves of PSO and related algorithms on f6圖6 PSO與相關算法對f6的迭代進化曲線

Figure 7 Iterative evolution curves of PSO and related algorithms on f7圖7 PSO與相關算法對f7的迭代進化曲線

Figure 8 Iterative evolution curves of PSO and related algorithms on f10圖8 PSO與相關算法對f10的迭代進化曲線

4.3.3 IRBHPSO穩定性分析

算法的穩定性也是算法尋優能力的重要體現。為了進一步驗證IRBHPSO的優越性,本節比較了表3中各算法對不同基準測試函數運行結果的標準差。

從表3可知,除f9、f11和f12外,在其他基準測試函數上,IRBHPSO運行結果的標準差都小于或者約等于PSO運行結果的標準差,表明IRBHPSO具有較好的穩定性和魯棒性。在f11和f12上,雖然IRBHPSO的標準差不及PSO的,但是依然保持了較高的水平,IRBHPSO的穩定性和魯棒性依舊較好。僅在f9上,IRBHPSO的標準差與PSO的相差較大,穩定性差于PSO的。綜上,IRBHPSO在11個基準測試函數上都具有較好的穩定性,并且在9個基準測試函數上的穩定性優于PSO的,以上表明IRBHPSO的穩定性對比PSO的得到了較大的提升。IRBHPSO的良好穩定性是因為本文引入的3種改進策略平衡了算法的全局探索能力和局部尋優能力,使得IRBHPSO在相同的實驗次數下可以更多次以更高的精度收斂到理想最優值附近,提高了算法的穩定性,在面對復雜問題時可以更好地尋優。

綜合考慮算法收斂精度、收斂速度以及穩定性,在f1、f2、f3、f4、f5、f6、f7、f8和f10上,IRBHPSO的評價指標值都優于PSO的;在f11和f12上,雖然IRBHPSO的穩定性不如PSO的,但是IRBHPSO的收斂精度與PSO的基本相同,仍有較高水平;僅在f9上,IRBHPSO未展現出較好的優化效果。以上結論表明,IRBHPSO克服了PSO收斂速度慢和易早熟、易陷入局部最優等缺點,提高了算法的收斂精度和收斂速度,增強了算法的穩定性,驗證了IRBHPSO的優越性和本文所提改進策略的有效性。

4.4 不同改進策略對比

為了展示不同的改進策略對PSO尋優能力的影響,進一步驗證所提改進策略的有效性。本節將結合變尺度黑洞的PSO命名為PSO1,將結合混合策略位移系數的PSO命名為PSO2,將結合種群遷徙的BOA算子的PSO命名為PSO3。選取f1、f2、f5和f6,用PSO、PSO1、PSO2和PSO3分別對f1、f2、f5、f6獨立運行30次,得到各算法對基準測試函數運行結果的平均值(mean)、最優值(best)和標準差(std),如表4所示。為了比較改進策略對算法收斂速度的影響,本節列出各算法對不同基準測試函數的迭代進化曲線,如圖9～圖12所示。

Table 4 Comparison ofoptimization results of PSO and single-strategy improved PSO algorithms表4 PSO與單策略改進PSO算法尋優結果對比

考慮算法的收斂精度,由表4可知,除PSO3對f5的優化結果,其他單策略改進的PSO對f1、f2、f5和f6的收斂精度相較于PSO的均得到了提升或者持平。同時,從表4還可以看出,PSO1的收斂精度是3種改進算法中最差的,但其收斂精度相較于PSO的仍有一定的提升。綜上,PSO1、PSO2和PSO3的收斂精度相較于PSO的都得到了一定的提升,表明本文所提的3種改進策略都可以在一定程度上提高算法的收斂精度,驗證了所提改進策略的有效性。

考慮算法收斂速度,從圖9～圖12中可以看出,PSO3在f1、f2、f5和f6上收斂速度極快,PSO1和PSO2的收斂速度略優于PSO的,表明本文所提改進策略可以有效改善PSO收斂速度慢的問題,增強算法的全局尋優能力,表明在本文所提3種改進策略中,PSO3中的策略在提升算法收斂速度上發揮了主要作用。

Figure 9 Iterative evolution curves of PSO and single-strategy improved PSO algorithms on f1圖9 PSO與單策略改進PSO算法對f1的迭代進化曲線

Figure 11 Iterative evolution curves of PSO and single-strategy improved PSO algorithms on f5圖11 PSO與單策略改進PSO算法對f5的迭代進化曲線

Figure 12 Iterative evolution curves of PSO and single-strategy improved PSO algorithms on f6圖12 PSO與單策略改進PSO算法對f6的迭代進化曲線

考慮算法穩定性,從表4可知,除PSO3對f5運行結果的標準差外,3種改進算法運行結果的標準差都低于PSO運行結果的標準差,表明本文所提的改進算法比PSO更穩定,可以更有效地進行尋優。雖然PSO3對f5運行結果的標準差較大,但PSO3在f1、f2和f6上的標準差均小于PSO的標準差,表明PSO3中的改進策略可以有效提高算法的穩定性。所以,從總體上說,3種改進策略都可以提升PSO的穩定性,驗證了本文所提策略的有效性。

綜上,從3個評價指標的實驗結果可以看出,本文所提的3種改進策略都可以在一定程度上提升算法收斂精度、收斂速度和穩定性,改善了PSO收斂速度慢和易早熟、易陷入局部最優的問題,驗證了本文所提3種改進策略的有效性。

4.5 Wilcoxon秩和檢驗

為了進一步驗證IRBHPSO的優越性和本文所提改進策略的有效性,本節采用Wilcoxon秩和檢驗[19]進行統計分析,判斷比較IRBHPSO與其他算法之間是否有顯著性差異。將PSO、GSA、RBHPSO、BOA以及IRBHPSO分別在f1～f12上獨立運行15次,將IRBHPSO的15次尋優結果分別與PSO、GSA、RBHPSO和BOA進行Wilcoxon秩和檢驗,設置顯著水平為0.05。Wilcoxon秩和檢驗結果分析結果如表5所示。其中,H為檢驗的結果,W為顯著性判斷結果。若H<0.05,W為“+”,表明IRBHPSO的尋優結果顯著性優于其他算法的;若H>0.05,W為“-”,表明IRBHPSO的尋優結果與其他算法的無顯著性差異;若H=NaN,W為“”,表明無法進行顯著性判斷。

從表5可以看出,在f1、f2、f3、f4、f6和f7上,相較于其他算法,IRBHPSO的尋優結果具有顯著性的優勢。對于f5,IRBHPSO的尋優結果與GSA、RBHPSO的相比沒有顯著性優勢,但是相較于PSO的仍有顯著性優勢,表明IRBHPSO的尋優性能依舊優于PSO的。對于f8,除RBHPSO的尋優結果,IRBHPSO相較于其他算法的尋優結果均有顯著性優勢。對于f9,雖然IRBHPSO與4種算法對比的H值都很小,但這是因為在f9上IRBHPSO的表現較差,導致其他算法的尋優結果顯著優于IRBHPSO的,從而使得IRBHPSO與其他算法的尋優結果有顯著性差異。在f10～f12上,IRBHPSO與其他算法對比的H值多為NaN或者大于0.05,這是因為復合基準測試函數的維度都較小,算法容易收斂至理論最優附近,導致不同算法的尋優結果差距較小,而實際上所有算法都得到了較好的尋優效果。綜上,IRBHPSO在單模態基準測試函數上具有絕對的顯著性優勢,在大部分多模態基準測試函數上優勢明顯,在復合基準測試函數上有較高的收斂精度。以上結果表明,IRBHPSO相較于其他算法表現出了更好的尋優性能,競爭優勢明顯,驗證了IRBHPSO的優越性和本文所提改進策略的有效性。

Table 5 Results of Wilcoxon rank sum test 表5 Wilcoxon秩和檢驗結果

5 結束語

本文提出了一種基于變尺度黑洞和種群遷徙的PSO——IRBHPSO,在PSO的基礎上引入變尺度黑洞來平衡全局探索和局部尋優的權重;在算法位置更新策略中加入基于混合策略的位移系數,增強算法迭代前期的收斂能力和迭代后期的局部尋優能力;將基于種群遷徙的BOA作為局部算子加入PSO中,改善了PSO收斂速度慢、易陷入局部最優等問題。最后通過對基準測試函數的仿真實驗和Wilcoxon秩和檢驗驗證了本文所提IRBHPSO的優越性和改進策略的有效性。IRBHPSO克服了PSO收斂速度慢和易早熟、易陷入局部最優的缺點,在收斂精度和收斂速度上都有明顯的提升,體現出了算法優異的全局探索能力和局部尋優能力。由于IRBHPSO的研究處于初始階段,接下來將擴展本文算法在實際工程問題中的應用,例如IRBHPSO在微電網日調度運行優化、分布式電源配電網動態重構和船舶微電網故障重構等任務中的應用。