處理高考中力學綜合題的思維策略
李海珍
(河北省灤平縣第一中學)
力學是高中物理的主干內容,力學綜合題是高考中重點考查的內容,對考生的能力要求較高,要具有正確進行受力分析和運動分析的能力.此類問題主要涉及兩類規律,即物體的受力規律和物體的運動規律;重點考查兩種觀點,即動量觀點與動能觀點;問題處理的關鍵是弄清問題背景中出現的過程、狀態等.下面以2022年全國乙卷壓軸題為例,探究力學綜合問題的處理策略以及思維方法.
例(2022年全國乙卷)如圖1所示,一質量為m的物塊A與輕質彈簧連接,靜止在光滑水平面上;物體B向A運動,t=0時與彈簧接觸,到t=2t0時與彈簧分離,第一次碰撞結束,A、B的v-t圖像如圖2所示.已知從t=0到t=t0時間內,物塊A運動的距離為0.36v0t0.A、B分離后,A滑上粗糙斜面,然后滑下,與一直在水平面上運動的B再次碰撞,之后A再次滑上斜面,達到的最高點與前一次相同.斜面傾角為,與水平面光滑連接,碰撞過程中彈簧始終處于彈性限度內,求:
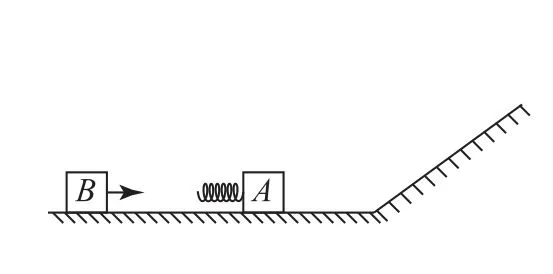
圖1

圖2
(1)第一次碰撞過程中,彈簧彈性勢能的最大值;
(2)第一次碰撞過程中,彈簧壓縮量的最大值;
(3)物塊A與斜面間的動摩擦因數.
1 科學嚴謹審題
審題是解題的第一步,也是決定問題能否順利求解的關鍵環節.力學綜合問題通常敘述冗長,信息量大,運動過程復雜,審題中要注意關鍵詞語,從中挖掘出隱含條件,據此梳理解題思路,建立相應的物理模型,進而找到問題求解的突破口.
2 扎實理論基礎
牛頓運動定律、動量定理、動能定理、機械能守恒定律、動量守恒定律是力學的基本理論,這些理論構成了解決力學問題的基石,學習過程中要注意強化這些理論在不同物理情境中的靈活運用.例如,對于單個物體,若涉及時間問題,常優先選動量定理;若涉及位移問題,則優選動能定理;對于多物體系統,應優先選用兩個守恒定律;若涉及系統內物體的相對位移及摩擦力等,則要注意應用功能關系,分析運動過程的轉折點等.
3 明晰運動過程
力學綜合問題通常涉及多個過程,求解時可將其分解為多個子過程,再對每個子過程進行分析,列出相應的方程.
本題中物體B以一定的速度向右運動,撞向彈簧,把彈簧壓縮至最短,此時兩物體共速,彈簧的彈性勢能最大.共速后彈簧張開,同時繼續向右運動,彈簧恢復到原長,兩物體分開,第一次碰撞結束.整個運動過程,如圖3所示.

圖3
從這一過程,我們可得到哪些信息?
從原長到最短的過程中,彈簧的彈性勢能增加,最短的時候,彈性勢能最大,隨著彈性勢能的釋放,轉化為兩物體的動能.從全程來看彈簧的彈性勢能先增加后減小到0,整個過程中彈性勢能的變化量為0,若將兩物體和彈簧視為一個系統,在運動過程中整個系統彈性勢能的初末狀態均為0,故動能沒有變化,這說明碰撞過程中系統的動能無損失,即這一過程屬于完全彈性碰撞,遵循動量守恒定律和機械能守恒定律.
下面對第(1)問進行討論.
設B的質量為M,由動量守恒定律得M?1.2v0=(M+m)v0,解得M=5m.由機械能守恒定律可得,得.
4 挖掘題目本質
第一次碰撞過程中,彈簧壓縮量的最大值,即為彈簧壓縮最短時.如圖4所示,在共速前物塊B的速度大于A的速度,彈簧被壓縮.當二者共速時,彈簧的壓縮量達到最大值,之后隨著物塊A的速度大于B的速度,彈簧逐漸伸長.如果物塊A、B中間沒有彈簧,則碰撞后二者連在一起,位移相等.而本題此運動過程中物塊B的位移xB大于A的位移xA,彈簧的壓縮量就是物塊B比A多走的位移,我們只要求出0~t0這段時間內物塊B的位移xB即可,xB-xA就是彈簧的最大壓縮量.二者的位移差即圖5中陰影部分的面積,即物塊B的v-t圖像與橫軸圍成圖形的面積與A的v-t圖像與橫軸圍成圖形的面積之差.
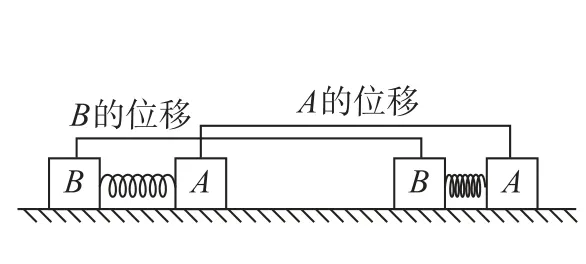
圖4

圖5
物塊A、B第一次碰撞分離后,A滑上粗糙斜面,然后滑下,與一直在水平面上運動的B再次碰撞,由于斜面是粗糙的,所以A滑上的速度與滑下的速度不同,之后物塊A再次滑上斜面,達到的最高點與前一次相同,那么物塊A第一次滑上斜面時,速度是2v0,第二次滑上斜面時,因為達到的高度相同,故也是2v0.
通過分析發現第(2)問考查了“人船模型”的拓展應用,第(3)問考查了斜面上往返的多過程問題以及彈性碰撞,這些內容源于教材,又高于教材.
弄清了問題的本質,就明確了解題的方向.
5 破解問題難點
本題的難點在于物塊B與彈簧接觸的過程中,彈簧彈力隨著彈簧形變量的變化而變化,物塊A和物塊B所受的合力以及加速度都是隨時間的變化而變化的,即為變加速的情況,且題目中沒有直接給出物塊A、B速度隨時間變化的函數關系,只給了t=0到t=t0時,物塊A的位移為0.36v0t0.位移對時間的變化率是速度,而速度函數在某段時間內的定積分即為位移.
對第(2)(3)問的解答如下.
(2)方法1設0~t0時間內,物塊A、B的速度分別為vA、vB,vA和vB是與時間有關的函數,則xA=.由動量守恒定律得M?1.2v0+m?0=MvB+mvA,得.因此
所以xB-xA=1.128v0t0-0.36v0t0=0.768v0t0.
另外此問也可利用位移等于速度在時間上的累積求解.
方法2設同一時刻物塊A、B的加速度分別為aA、aB,瞬時速度分別為vA、vB.同一時刻彈簧對物塊A、B的彈力大小相等,根據牛頓第二定律F=ma,可知同一時刻aA=5aB,則vA=aAt,vB=
據位移等于速度在時間上的累積可得xA=vAt,xB=vBt,已知xA=0.36v0t0,故xB=1.128v0t0,所以xB-xA=1.128v0t0-0.36v0t0=0.768v0t0.
(3)設物塊A第一次滑下斜面的速度大小為vA1,向左為正方向,由動量守恒定律可得
據能量守恒定律可得
聯立兩式解得vA1=v0.
設物塊A在斜面滑行的長度為L,對上滑過程由動能定理有-mgLsinθ-μmgLcosθ=0-,下滑過程由動能定理得mgLsinθμmgL?cosθ=,解得μ=0.45.
物理與數學是不可分割的整體,物理學的發展離不開數學的支撐.物理問題在經歷建立模型分析、運用規律之后,往往轉化成為數學問題,可借助數學知識和方法來求解.
(完)

