白銀最優(yōu)套保模型、套保比率及套保有效性

趙海濤 王曉星 曾樹峰 吳含英

摘?要：文章以上金所白銀延期和上期所白銀主力合約數(shù)據(jù)為研究對象，基于VaR和CVaR最優(yōu)套保模型視角，構(gòu)建了白銀現(xiàn)貨與期貨的GJR?Copula-N（t）模型，從靜態(tài)和動態(tài)角度對白銀最優(yōu)套保模型、套保比率及套保有效性進行度量和比較。結(jié)果表明：白銀期現(xiàn)貨市場具有動態(tài)聯(lián)動性的內(nèi)部結(jié)構(gòu)，動態(tài)GJR-Copula模型下的套保比率優(yōu)于靜態(tài)模型，且CVaR最小化目標套保策略下的套保比率要大于VaR策略。套保有效性衡量及模型準確性檢驗顯示，白銀套保有效性平均達到70%～80%，動態(tài)模型套保效果好于靜態(tài)模型，且CVaR模型的套保有效性優(yōu)于VaR模型，其中動態(tài)CVaR-GJR-t?Copula模型的套保效果最好，模型準確性最高，能最大限度地規(guī)避白銀現(xiàn)貨市場價格風險。關(guān)鍵詞：白銀期貨；最優(yōu)套保比率；VaR；CVaR；GJR-Copula；套保有效性

作者簡介：

趙海濤（通訊作者），

經(jīng)濟師，經(jīng)濟學碩士，研究方向為金融市場與金融分析、套期保值；

王曉星，經(jīng)濟師，經(jīng)濟學碩士，研究方向為風險管理；

曾樹峰，高級會計師，經(jīng)濟學碩士，研究方向為套期保值核算及套期會計；吳含英，經(jīng)濟師，經(jīng)濟學碩士，研究方向為金融市場與金融分析、套期保值及金融風險。

①?數(shù)據(jù)來源：新華社。

②?數(shù)據(jù)來源：新浪財經(jīng)。

一、引言

繼續(xù)擴大對外開放，推動我國開放型經(jīng)濟向更高層次發(fā)展是黨的二十大報告核心內(nèi)容之一。近年來隨著我國金融業(yè)對外開放程度進一步擴大，與國外金融市場的聯(lián)動性不斷加強。2019年7月20日，國務(wù)院金融委宣布11條金融業(yè)對外開放措施，接著證監(jiān)會宣布于2020年1月1日起，取消期貨公司外資股比限制

①

，這些政策措施的實施推動了國內(nèi)外期貨市場的聯(lián)系，相應(yīng)地，聯(lián)動性的加強也意味著國內(nèi)商品價格的波動越來越頻繁，外來沖擊對國內(nèi)商品價格的影響越大。黨的十八大以來，中國經(jīng)濟進入新常態(tài)，特別是2020年新冠疫情暴發(fā)以來，全球經(jīng)濟遭受重創(chuàng)，加之美國高通脹疊加美聯(lián)儲加息預(yù)期的影響，國際大宗商品價格出現(xiàn)的巨幅波動使相關(guān)企業(yè)的生產(chǎn)經(jīng)營面臨巨大風險，其中資本市場引人矚目的如中行“原油寶”事件和青山鎳逼空事件至今都令人深思②。與此同時國內(nèi)期貨市場也出現(xiàn)了歷史性突破與發(fā)展，企業(yè)為規(guī)避價格風險而參與期貨套期保值的需求越來越迫切。作為貴金屬的白銀兼具商品屬性與金融屬性，在國內(nèi)外經(jīng)濟發(fā)展中均扮演著重要角色。中國是白銀產(chǎn)需大國，2012年以前缺少平抑價格波動的有效工具，很多白銀產(chǎn)銷主體難以較好地控制市場風險。自2012年5月10日和2013年7月5日白銀期貨在上海期貨交易所上市和夜盤交易以來，吸引了市場的廣泛關(guān)注。截至2020年年底，上海黃金交易所白銀成交量為42147萬噸，同比增長13678%，成交額為2075萬億元，同比增長18619%；上海期貨交易所白銀成交量為107170萬噸，同比增長2506%，成交額為5558萬億元，同比增長5544%

數(shù)據(jù)來源：上海期貨交易所和上海黃金交易所官網(wǎng)。。在此背景下，考慮到白銀像大多數(shù)大宗商品一樣在生產(chǎn)、制造、貿(mào)易等領(lǐng)域具有十分重要的地位，同時作為正常流通的特殊金屬，白銀容易受到宏觀經(jīng)濟政策、地緣政治等因素的影響，特別是在后疫情時代，中國和其他國家一樣面臨經(jīng)濟下行壓力，加之全球經(jīng)濟金融政策等不確定性達到前所未見的高度，使得眾多白銀主體加大對白銀的套保需求，并借助白銀相關(guān)衍生品進行點價交易，進行相關(guān)性套保，開展白銀進出口貿(mào)易等。因此，在上述需求加大的情況下，本文旨在度量和比較不同風險偏好下的白銀最優(yōu)套保模型和套保比率，這對加強白銀價格風險管理、合理化套保策略及最小化白銀套保成本都有重要的現(xiàn)實意義。

二、文獻綜述

自馬科維茨投資組合理論產(chǎn)生以來，學界就將現(xiàn)貨和期貨資產(chǎn)作為一種投資組合進行研究。隨后，最優(yōu)套保比率、最優(yōu)套保模型和套保有效性問題就一直成為國內(nèi)外研究和考察的重點和熱點。

已有關(guān)于套保比率的研究集中于兩個方向：一是基于效用最大化的套保比率模型研究，該模型通過最大化效用函數(shù)獲得最優(yōu)套保比率；二是風險最小的套保比率模型研究，該模型通過使得方差最小化，即特定風險最小化來測算最優(yōu)套保比率，也是傳統(tǒng)意義上的最小化投資組合方差模型。Johnson和Stein提出了計算投資組合最小方差的套保比率，隨后經(jīng)Ederington等在金融期貨領(lǐng)域加以推廣，成為現(xiàn)代套期保值比率理論的雛形，隨著計量經(jīng)濟學的發(fā)展，產(chǎn)生了基于ECM類和GARCH類的均值-方差套保比率模型。目前，眾多風險度量工具相繼被采用，如平均擴展基尼系數(shù)、VaR最優(yōu)套保比率模型等。

關(guān)于套保模型的研究也分為兩大類：其一，靜態(tài)套保模型，該類模型常見的策略為MV模型中相關(guān)系數(shù)為1的模型、套保比率為1的Naive策略和普通最小二乘法套保策略；其二，動態(tài)套保模型，該模型主要基于動態(tài)變化思想進行研究。隨后，由于信息技術(shù)的快速發(fā)展，基于動態(tài)思想的研究不斷涌現(xiàn)。

因金融資產(chǎn)具有“尖峰厚尾”、波動聚集、有偏、非對稱、非線性等特征，上述或靜態(tài)或最小化方差套保比率模型已不能精確度量最優(yōu)套保比率并進行套保決策，因此，現(xiàn)代套期保值理論已不再是簡單建立一個與現(xiàn)貨頭寸方向相反、數(shù)量相等的期貨頭寸，而是將期現(xiàn)頭寸二者看作一個組合，綜合考慮套保者的動機、風險偏好、風險損失承受能力等因素，對期現(xiàn)頭寸比率進行優(yōu)化的理論。近年來，隨著Copula函數(shù)理論的發(fā)展，人們將其與GARCH類、最小下偏距（LPM）、VaR（CVaR）模型結(jié)合，并融入Markov狀態(tài)轉(zhuǎn)換思想來運用到套保比率的研究中。經(jīng)過對文獻的整理可以發(fā)現(xiàn)，當前基于Copula函數(shù)的最優(yōu)套保比考察集中在以下三方面：第一，基于Copula函數(shù)的最小方差套保比研究，該類研究將動態(tài)Copula函數(shù)引入刻畫金融資產(chǎn)的序列相關(guān)結(jié)構(gòu)的動態(tài)性。第二，基于Copula函數(shù)的最小下偏距（LPM）套保比率研究，該類研究從套保者目標回報和風險偏好出發(fā)，同時結(jié)合Copula函數(shù)進行研究。第三，基于VaR（CVaR）的套保比研究，該類研究基于在險價值和條件在險價值的風險管理角度進行最優(yōu)套保比的研究。

通過對以上文獻的梳理可知，雖然已有研究都在尋求最優(yōu)套保模型以估計最優(yōu)套保比率，但套保的原理是相同的，而從考察套保對象的角度看卻千差萬別，沒有關(guān)注套保對象本身。本研究旨在考察白銀現(xiàn)貨與期貨的套保問題，而現(xiàn)有文獻對其的研究并不多見。鑒于此，文章的邊際貢獻主要體現(xiàn)在三個方面：一是從風險管理的角度，引入VaR（CVaR）模型，將白銀期現(xiàn)貨看作一個資產(chǎn)組合，并結(jié)合套保者的風險偏好、基差風險來考察；二是考慮到金融資產(chǎn)的“尖峰厚尾”等特征，將不同分布、不同置信水平下的套保比率進行比較分析；三是構(gòu)造動態(tài)的Copula-GJR模型，試圖找到白銀套期保值的最優(yōu)套保比率，并進行套保效果的衡量比較和模型的準確性檢驗。

三、研究設(shè)計

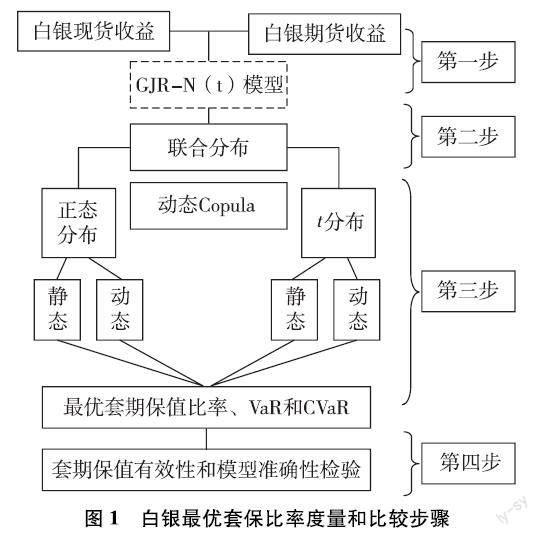
文章對白銀期貨市場最優(yōu)套保比率的度量和比較主要分為四個步驟：第一步，在傳統(tǒng)最優(yōu)套期保值比率決策模型的基礎(chǔ)上引入VaR和CVaR思想，導出最優(yōu)套期保值比率模型基本構(gòu)型；第二步，運用GJR-N（t）模型對白銀期現(xiàn)貨收益率建模，得到聯(lián)合分布函數(shù)；第三步，對聯(lián)合分布函數(shù)運用動態(tài)因子Copula模型構(gòu)建白銀期現(xiàn)貨收益率間的相關(guān)性模型，模擬出不同分布、不同風險偏好下的最優(yōu)套保比率；第四步，一方面使用方差減小法和修正的夏普比率（ASR）綜合測度白銀的套期保值有效性，另一方面采用貝葉斯檢驗法對文章構(gòu)建的套期保值模型進行準確性檢驗（圖1）。

（一）傳統(tǒng)最優(yōu)套保比率決策模型

傳統(tǒng)的套保比率是在假設(shè)現(xiàn)貨和期貨市場價格變動方向相同、大小相等的基礎(chǔ)上確定的，其比率設(shè)為1。在套期保值實踐中，最小化風險（方差）模型運用較為普遍，它假設(shè)某一包含現(xiàn)貨和期貨的資產(chǎn)組合（以空頭為例），在t時刻，該投資者持有cs，t單位的現(xiàn)貨多頭頭寸和cf，t單位的期貨空頭頭寸，則該資產(chǎn)組合在t時刻的收益率和收益率方差分別為：

rp，t=cs，tps，trs，t－cf，tpf，trf，tcs，tps，t=rs，t－h(huán)trf，tσ2p，t=σ2s，t+h2tσ2f，t－2htσsf，t（1）

其中，ps，t為t時刻的現(xiàn)貨價格，pf，t為t時刻的期貨價格，rs，t為現(xiàn)貨的收益率，rf，t為期貨的收益率，ht為t時刻資產(chǎn)組合的套期保值比率，σ2i，t為現(xiàn)貨收益率的方差，σ2f，t為期貨收益率的方差，σs，t為現(xiàn)貨與期貨收益率的協(xié)方差。為求得最優(yōu)套保比率，對式（1）中的組合方差對ht求一階導令其為0，可得數(shù)學表達式：

ht=σsf，tσ2f，t=ρtσs，tσf，t（2）

式中，h*t為t時刻資產(chǎn)組合的最優(yōu)套保比率，ρt為t時刻現(xiàn)貨與期貨價格變動的相關(guān)系數(shù)。最小化風險模型要求方差最小，但該模型未考慮“投機需求”部分，且不能明確風險損失程度大小，因此，實際運用中存在較大缺陷。

（二）基于VaR和CVaR視角的最優(yōu)套保比率模型

VaR即在險價值，是指“處于風險中的價值”，其定義為在給定的置信水平（α）和時間期內(nèi)，某一金融資產(chǎn)或資產(chǎn)組合預(yù)期可能發(fā)生的最大損失，其表達式為

Probrt≤－VaR=1－α?（3）

通常將VaR值取正，故在上式VaR前面加負號。

CVaR是指在給定的置信水平（α）和時間期內(nèi)，某一金融資產(chǎn)或資產(chǎn)組合面臨的超過VaR的損失，其表達式為

CVaRα=Ert≥－VaRα=11－α∫

－VaRαpfpdp（4）

CVaR的數(shù)學和統(tǒng)計特性較好，在進行投資組合優(yōu)化時，其是權(quán)重的凸函數(shù)，且其相對于VaR對置信水平是連續(xù)的，因而是一種更加保守的風險度量手段。而實踐中，套保比率是一個隨時間動態(tài)變化的過程，同時也要考慮資產(chǎn)組合面臨的損失和超出一定風險范圍的損失，文章擬選擇該模型進行比較分析。

假設(shè)套期保值資產(chǎn)組合（持有期貨空頭頭寸的情形）的收益率服從正態(tài)分布，根據(jù)定義和中心極限定理，含有套保比率的VaR和目標函數(shù)為

Prp，t≤－VaRht

=Prp，t－Erp，tσp，t≤－VaRht－Erp，tσp，t

=Φ－VaRht－Erp，tσp，t=1-α（5）

VaRht=-Erp，t+Φ-1ασp，t=Φ-1ασ2s，t+h2tσ2f，t－2htσsf，t+htErf，t-Ers，t?（6）

其中，σp，t為套期保值組合收益率的標準差，E（·）為收益率的期望值，Φ（·）為標準正態(tài)分布函數(shù)，Φ-1（α）為標準正態(tài)分布函數(shù)α分位數(shù)。則CVaR（ht）可通過式（4）進一步得到：

CVaRht=－Erp，t－Erp，tσp，trp，t－Erp，tσp，t≤Φ-1α

σp，t－Erp，t=－∫Φ-1α－

xΦxdx1-ασp，t－Erp，t=e（Φ-1（α））221-α2π

σ2s，t+h2tσ2f，t－2htσsf，t+htErf，t-Ers，t?（7）?

若令D1（α）=Φ-1（α）;D2（α）=

e-（Φ-1（α））22（1-α）2π，則在正態(tài)分布情形下，式（6）和式（7）可簡化為

VaRht=-Erp，t+D1ασp，tCVaRht=-Erp，t+D2ασp，t（8）

由于金融資產(chǎn)收益的波動具有明顯的“尖峰厚尾”特征，并不符合正態(tài)分布的假設(shè)，而t分布能夠較好地擬合收益序列的厚尾性而被廣泛運用，本文借鑒王炎的研究，簡化煩瑣的證明過程，得到收益率序列服從t分布情況下的VaR和CVaR表達式：

VaRht=-Erp，t+D3ασp，tCVaRht=－Erp，t+D4ασp，t?（9）

其中，D3（3）=t*1-α（v）

vv-2；D4α=

υΓυ+121-αυ－1υπΓυ21+t21－αυυ1－υ2，α為置信水平，Γ（·）稱為Γ函數(shù)，其定義域在（0，+∞），則有Γ（υ+1）=υΓ（υ）；t*1-a（v）表示自由度為υ的標準化t分布的1-α點分位數(shù)，υ>2。就式（6）對ht求一階導并令其為0，求解方程得到兩個非負根，其對應(yīng)的點為極小值點，通過比較其對應(yīng)的VaR，可以確定正態(tài)分布下的基于VaR的最優(yōu)套保比率，同理可得基于CVaR的最優(yōu)套保比率：

hNVaR=ρsf，tσs，tσf，t-Erf，tσs，tσf，t

1－ρ2sf，tD1α2σ2f，t－Erf，t2（10）

hNCVaR=ρsf，tσs，tσf，t-Erf，tσs，tσf，t

1－ρ2sf，tD2α2σ2f，t－Erf，t2?（11）

同理，也可求得t分布下基于VaR和CVaR的最優(yōu)套保比率：

hTVaR=ρsf，tσs，tσf，t-Erf，tσs，tσf，t

1－ρ2sf，tD3α2σ2f，t－Erf，t2（12）

hTCVaR=ρsf，tσs，tσf，t-Erf，tσs，tσf，t

1－ρ2sf，tD4α2σ2f，t－Erf，t2（13）

從以上四式可以看出，最優(yōu)套保比率可以分解為反映純套保和投機需求兩部分。純套保部分ρsf，t*σs，t/σf，t就是最小方差套保比，投機需求則為后半部分，與白銀主體的風險態(tài)度相關(guān)，取值于置信水平（α）的大小。套保者越厭惡風險，置信水平（α）就會越高，即套保比率越大。

（三）構(gòu)建聯(lián)合分布模型

在確定基于VaR和CVaR的最優(yōu)套保比率模型后，接下來需要設(shè)定現(xiàn)貨和期貨收益率的邊際分布模型，考慮到現(xiàn)實生活中金融資產(chǎn)之間的相關(guān)性并不是線性相關(guān)的，往往具有自相關(guān)、異方差、“尖峰厚尾”、波動聚集等特征，本文以Glosten等提出的GJR模型為基礎(chǔ)，引入具有誤差修正項（基差變化）的GJR模型來估計白銀現(xiàn)貨與期貨收益率條件方差及殘差的密度函數(shù)：

ri，t=ci+λilnps，t－1－lnpf，t－1+ci，1ri，t－1+ei，tei，t=σi，tzi，t|zi，t～D·σ2i，t=φi+ai，1e2i，t－1+biσ2i，t－1+ai，2ki，t－1e2i，t－1?（14）

白銀現(xiàn)貨與期貨的收益率序列取對應(yīng)時點價格對數(shù)差分乘以100獲得，rit=100*（lnpit-lnpit-1）即當期資產(chǎn)的收益率，令i=s或f代表現(xiàn)貨和期貨，pit，pit-1為t和t-1時刻的價格，ci為截距項，（lnps，t-1-lnpf，t-1）為誤差修正項，反映期現(xiàn)基差變動對收益率的影響；ci，1為滯后一期收益率對當期收益率的影響；ei，t為資產(chǎn)i在t時刻的殘差序列，σi，t為時刻t收益率的條件波動率，φi，ai，1，bi和ai，2為待估參數(shù)，參數(shù)ai，1+bi+05ai，2的大小反映了收益率序列波動的持續(xù)性，ai，2反映了前一期利好或利空消息對當期期現(xiàn)市場非對稱影響參數(shù)，用以衡量“杠桿效應(yīng)”，若其顯著非零反映了消息對收益率波動的影響是非對稱的，ki，t-1為虛擬變量，當ei，t-1＜0，ks，t-1=1，反之ks，t-1=0，為保證條件波動率為正值，一般要求φi＞0，ai，1≥0，bi≥0，ai，1+05ai，2≥0。zi，t為根據(jù)序列rit的分布特征服從一定的分布，D（·）為正態(tài)分布或自由度為v的t分布函數(shù)。

（四）動態(tài)因子Copula模型構(gòu)建

在確定了單個變量的邊緣分布之后，為更好地描述期現(xiàn)市場間收益的相關(guān)性結(jié)構(gòu)（尾部相關(guān)性），文章擬選擇合適的Copula函數(shù)從時變角度來探究金融資產(chǎn)間的尾部相關(guān)性。目前，使用較多的是Gaussian?Copula（G-Copula）和t?Copula，普通Gaussian?Copula和普通t?Copula的條件密度函數(shù)分別為

CG－Copulaμ，υ;ρ=

11－ρ2expΦ－1μ2+Φ－1υ2－2ρΦ－1μΦ－1υ2ρ2－1

exp－Φ－1μ2Φ－1υ22（15）

Ct－Copulaμ，υ;ρ，η=11－ρ2

Γη+22Γη2Γη+1221+ξ12+ξ22+2ρξ1ξ2η1－ρ2－η+2η∏2i=11+ξi2η－η+2η（16）

其中，Φ-1（·）是標準正態(tài)分布函數(shù)Φ（·）的逆函數(shù)，

t-1η（·）是t分布函數(shù)tη（·）的逆函數(shù)，η為自由度，ζ1=t-1n（μ），ζ2=t-1n（v），ρ為相依性參數(shù)；μ=D（rst），v=D（rft），為現(xiàn)貨收益率和期貨收益率的標準化殘差序列經(jīng)估計的邊緣分布函數(shù)進行累計概率積分變換后得到的新序列。考慮到金融資產(chǎn)收益率處于不斷變化中，本文參照現(xiàn)有文獻的研究，令Gaussian?Copula和t?Copula模型的相關(guān)系數(shù)服從以下動態(tài)變化過程，則得到TVP-Copula：

ρGt=

Λγ0+γ1ρt－1+γ2110∑10j=1|Φ－1μt－j－Φ－1υt－j|（17）

ρTt=

Λγ0+γ1ρt－1+γ2110∑10j=1|t－1μt－j－t－1υt－j|（18）

其中，Λ（·）是Logistic函數(shù)，Λ（x）=（1-e-x）/（1+e-x）是為了保證相關(guān)系數(shù)始終在（0，1）內(nèi)。

（五）套保有效性及模型準確性衡量

（1）套保有效性的衡量

套期保值的目的主要是規(guī)避現(xiàn)貨市場價格的波動風險，文章一方面以估計得到的VaR（CVaR）作為風險測度指標，通過方差減小法直接測度套保有效性；另一方面使用經(jīng)VaR（CVaR）、偏度和峰度作為風險進行調(diào)整的修正的夏普比率（ASR）度量單位風險產(chǎn)生的超額收益。相應(yīng)的評價公式為

H=VaRrs，t－VaRrp，tVaRrs，t×100%或

CVaRrs，t－CVaRrp，tCVaRrs，t×100%（19）

ASR=SR1+S6SR－K24SR2，SR=

Erp，t－rnVaRrp，t×100%或Erp，t－rnCVaRrp，t×100%（20）

其中，VaR（rs，t）（CVaR（rs，t））為未套保白銀收益率的風險價值（條件風險價值），VaR（rp，t）（CVaR（rp，t））為白銀套保組合收益率的風險價值（條件風險價值），H越大，則風險降低程度越大，套保策略規(guī)避風險能力越強，套保效果越好。SR是經(jīng)VaR（CVaR）調(diào)整的夏普比率，S和K是未套保白銀和白銀套保組合收益率序列的偏度和峰度，E（rp，t）為套保組合收益率，rn為無風險利率，用活期存款利率表示，同時作為比較業(yè)績基準，ASR越大，表明套保組合在單位風險下的超額組合收益越大，套保效果越好。

（2）套保模型準確性檢驗：貝葉斯檢驗

在使用VaR和CVaR估計模型參數(shù)時，由于其是一個統(tǒng)計估計量，準確程度受到估計誤差、模型假設(shè)、隨機因素，特別是樣本容量的影響，若使用不當，會造成低估或高估風險，不利于套保主體進行風險管理，因此，有必要對風險價值進行檢驗和評估。本研究以失敗檢驗法為基礎(chǔ)，使用有別于傳統(tǒng)的檢驗法即貝葉斯檢驗法對文中的套保模型進行準確性檢驗。

貝葉斯檢驗法基于失敗檢驗法框架，在失敗天數(shù)k服從二項分布B（T，p）時，根據(jù)貝葉斯原理，可得到p的后驗分布為

fp|k=1Bk+1，T－k+1pk+1－11－pT－k+1－1?（21）

由此可知，p的后驗分布為B（k+1，T-k+1），設(shè)p的置信水平為1-β的置信區(qū)間為［p1，pu］，然后采取統(tǒng)計上的參數(shù)估計方法，得到失敗率p（k/T）的置信區(qū)間，再利用假設(shè)檢驗思想，得出失敗天數(shù)k的接受域，由于k=Tp，可以得到給定置信水平α下的p的置信區(qū)間，若失敗率落于置信區(qū)間［p1，pu］內(nèi)，則文章構(gòu)建的套期保值型模準確的，反之，模型構(gòu)建存在瑕疵，拒絕接受該模型，具體公式：

p1=k+1k+1+T－k+1×Fβ/22T－k+1，2k+1，pu=k+1k+1+T－k+1×F1－β/22T－k+1，2k+1（22）

四、實證分析

（一）數(shù)據(jù)來源及初步判斷

因上海黃金交易所（上金所）白銀延期Ag（T+D）具有準現(xiàn)貨與準期貨的特征，目前市場大多以此為基準進行現(xiàn)貨定價，因此，本研究選擇上金所Ag（T+D）合約價格作為現(xiàn)貨（平水情況下）數(shù)據(jù)，選取上海期貨交易所（上期所）白銀主力合約價格作為對應(yīng)的期貨數(shù)據(jù)。另外，因套期保值隨業(yè)務(wù)常態(tài)發(fā)生，本文以30分鐘收盤數(shù)據(jù)為規(guī)則各選取兩市對應(yīng)數(shù)據(jù)作為期現(xiàn)數(shù)據(jù)，樣本期間為2019年1月16日至2022年9月9日，將2019年1月16日至2022年5月10日的2302對數(shù)據(jù)作為樣本內(nèi)數(shù)據(jù)；將2022年5月11日至2022年7月9日的118對數(shù)據(jù)作為樣本外數(shù)據(jù)，同時為保持兩市交易時間一致性和數(shù)據(jù)有效性，剔除不在同一時間段內(nèi)的數(shù)據(jù)。所有數(shù)據(jù)均來自Bloomberg。文中所有計算結(jié)果均通過Eviews11、R401和MATLAB2020a等軟件實現(xiàn)。

表1顯示了樣本期內(nèi)白銀現(xiàn)貨和期貨對數(shù)收益率序列的統(tǒng)計分析結(jié)果。可以看出，白銀期現(xiàn)貨的均值、極值和標準差差異不大，具有相同的變化特征；從偏度和峰度值看，兩序列均表現(xiàn)出“尖峰厚尾”特點；J-B統(tǒng)計量反映兩序列在1%的顯著性水平下拒絕正態(tài)分布的原假設(shè)；對各收益率序列進行ARCH-LM檢驗發(fā)現(xiàn)，其存在條件異方差性，可以構(gòu)建GARCH模型；Ljung-Box統(tǒng)計量顯示兩序列存在高階序列相關(guān)；同時ADF檢驗結(jié)果顯示所有序列在1%顯著水平下拒絕具有單位根，說明收益率序列是平穩(wěn)的。

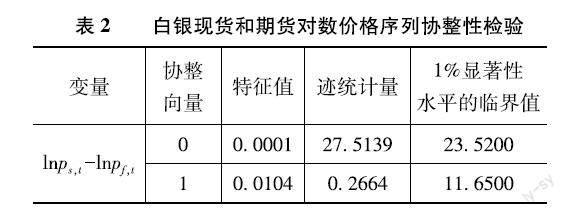
另外，由于期現(xiàn)貨價格隨著到期日的臨近會趨于收斂，因此基差變化對套期保值會產(chǎn)生重要影響。為此，文章構(gòu)建了有誤差項的GJR模型，并對白銀期現(xiàn)貨對數(shù)價格進行Johansen協(xié)整性檢驗，結(jié)果如表2所示。

從檢驗結(jié)果看出，白銀的期現(xiàn)價格序列間在1%顯著性水平下拒絕存在0個協(xié)整向量的原假設(shè)，至少存在一個協(xié)整向量的原假設(shè)不能被拒絕，說明二者間存在顯著的協(xié)整關(guān)系。再者，檢驗結(jié)果也說明文章在構(gòu)建邊緣分布模型時考慮誤差修正項是合適的。

（二）邊緣分布模型參數(shù)估計

邊緣分布的合理與否對套期保值效果的優(yōu)劣會產(chǎn)生重要影響，基于以上初步分析，為得到白銀現(xiàn)貨和期貨收益率序列邊緣分布模型的最佳擬合效果，文章對收益率序列進行反復擬合檢驗，同時設(shè)定標準化殘差分別服從正態(tài)分布和t分布進行比較，參數(shù)估計結(jié)果如表3所示。

從估計結(jié)果來看，整體上白銀現(xiàn)貨和期貨的高階序列相關(guān)性和ARCH效應(yīng)都已被消除，AIC、BIC和LLF結(jié)果反映t分布下的模型擬合效果較好，且自由度參數(shù)υ在1%水平下顯著，能準確刻畫白銀期現(xiàn)貨市場的“尖峰厚尾”等非對稱特征，更貼近市場實際情況。

具體而言，白銀期現(xiàn)貨殘差在服從正態(tài)分布和t分布下擬合的參數(shù)值相近且符號相同，說明期現(xiàn)貨間具有相同的變化特征和相同的影響因素；

均值方程中，誤差修正項系數(shù)均在1%顯著性水平下為正，說明白銀期現(xiàn)貨對數(shù)價格即基差變化隨著時間的后移會對收益率（不考慮資金成本）產(chǎn)生正向影響；ci，1非負，說明前期白銀收益率對當期收益率會產(chǎn)生影響；方差方程中，不對稱參數(shù)ai，2略大于0，表明利好消息對兩市的影響要大于利空消息產(chǎn)生的影響，兩市具有較弱的正“杠桿效應(yīng)”；ai，1+bi+05ai，2值接近1，反映了期現(xiàn)貨收益率序列波動效應(yīng)持續(xù)久。對收益率序列的邊緣分布進行K-S檢驗，各序列均在1%水平下通過檢驗，說明本文對邊緣分布的擬合是合理的。

（三）Copula模型參數(shù)估計

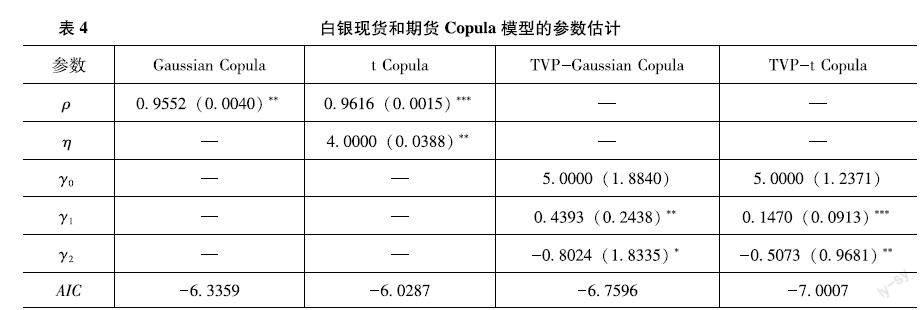
為進一步獲得白銀現(xiàn)貨與期貨收益率序列間的相關(guān)系數(shù)，本研究在得出邊緣分布擬合結(jié)果后，將現(xiàn)貨收益率和期貨收益率的標準化殘差序列帶入正態(tài)分布和t分布的累積分布函數(shù)中，得到μ=D（rst），υ=D（rft），再將其帶入正態(tài)分布的Gaussian?Copula、t分布的t?Copula以及動態(tài)的TVP-?Copula中，所得結(jié)果如表4所示，相關(guān)系數(shù)如圖2所示。

結(jié)合表4和圖2可知，Gaussian?Copula和t?Copula所得到的相關(guān)系數(shù)為固定常數(shù)09552和09616，并在樣本期間保持不變，屬于靜態(tài)相關(guān)系數(shù)，反映了白銀現(xiàn)貨和期貨具有正向相關(guān)性，但后者的相關(guān)性大于前者；動態(tài)TVP-Gaussian?Copula和TVP-t?Copula參數(shù)擬合結(jié)果顯示相關(guān)性表現(xiàn)出動態(tài)變化特征，樣本期內(nèi)的相關(guān)系數(shù)均值分別為09753和09791，其尾部截距項顯示的相關(guān)性均為5，說明白銀期現(xiàn)貨呈現(xiàn)正相依性，滯后項系數(shù)γ1在5%和1%置信水平下顯著，反映尾部相關(guān)性系數(shù)具有持續(xù)性，當期收益率間的相關(guān)性依賴于上期收益率變動，過去上尾收益率波動對當期收益率有正向影響，但t分布下的相關(guān)性要更大一些，這與各自括號內(nèi)標準差大小結(jié)果顯示一致。另外，從AIC結(jié)果來看，動態(tài)TVP-?t?Copula值最小，表明擬合效果最好。

（四）不同模型下套保比率估計結(jié)果比較

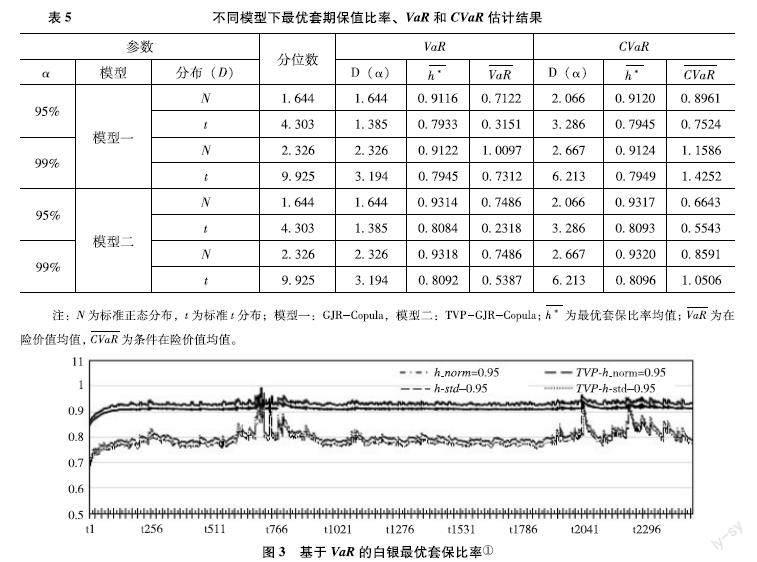
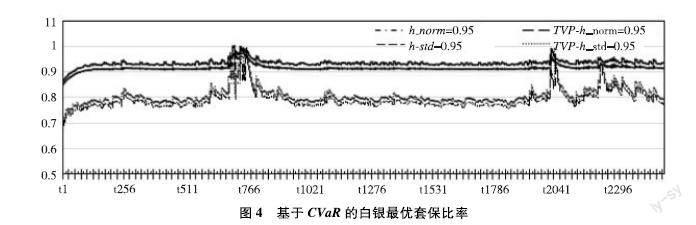
在對不同模型下的相關(guān)參數(shù)進行估計后，可得到白銀現(xiàn)貨與期貨在不同分布下的條件均值、條件標準差和相關(guān)系數(shù)序列，然后將其代入相應(yīng)式，即可求得不同模型在不同分布情況下對應(yīng)的VaR和CVaR模型下的套保比率、在險價值和條件在險價值，結(jié)果如表5、圖3和圖4所示。

從統(tǒng)計的縱向結(jié)果比較：①在同一置信水平下，模型二得到的套保比率、VaR和CVaR均較模型一的值要高，也即動態(tài)TVP-Gaussian?Copula和TVP-t?Copula下的結(jié)果比靜態(tài)Gaussian?Copula和t?Copula所得結(jié)果大，說明動態(tài)套保比率具有更大的靈活性，更符合實際情況，這與白銀期現(xiàn)貨市場相關(guān)性動態(tài)變化從而引起市場根據(jù)行情動態(tài)調(diào)整套保比率有關(guān)；

②同一模型相同分布下，平均套保比率隨著置信水平（α）的增大而增大，這一結(jié)果與以VaR或CVaR最小化目標套保策略和計算公式相佐證，α值反映了套保者對風險的厭惡程度，其越大，套保模型中“投機需求”部分越小；

③在VaR或CVaR最小化目標套保策略和相同分布下，隨著置信水平（α）的上升，相應(yīng)的VaR或CVaR值也明顯增大，套保者隨套保比率的變大而越來越厭惡風險；

④t分布下所得到的平均套保比率要明顯小于正態(tài)分布下的情形，說明t分布在擬合收益率序列分布時，能較為準確地描述金融資產(chǎn)的厚尾特征，使得套保者可以選擇適宜的套保策略來規(guī)避風險。

從統(tǒng)計的橫向結(jié)果比較：

①在同一置信水平（α）下，基于CVaR得到的套保比率略大于基于VaR得到的套保比率，但差異較小，說明利用模型求解套保比率的功能基本相同；②在同一置信水平（α）下計算得出的CVaR均值明顯大于VaR均值，這是由于VaR反映的是金融資產(chǎn)在一定期間內(nèi)一定置信水平下發(fā)生的最大損失，但沒有回答超過該置信水平下的損失，而CVaR量化了超過VaR的損失，是一種更為保守的風險度量工具。

另外，從動態(tài)TVP-GJR-Copula模型下的套保比率變化圖可以發(fā)現(xiàn)，在2022年3月和8月分別發(fā)生了套保比率的異常波動，第一個異常在3月，主要是由于新冠感染疫情暴發(fā)并在全球肆虐拖累經(jīng)濟，市場恐慌情緒彌漫促使資產(chǎn)拋售，白銀因工業(yè)屬性發(fā)揮導致其在本次危機中受到的負面影響更大而出現(xiàn)異常震蕩，連續(xù)重挫跌停達到近年來新低，現(xiàn)貨波動大于期貨波動；第二個異常在8月，主要由于為刺激經(jīng)濟恢復，利率下降、通脹預(yù)期穩(wěn)步上升和美元貶值而出現(xiàn)貴金屬急劇上漲行情，白銀因強勁的投資需求和工業(yè)需求拉動，創(chuàng)出近年來新高，致使現(xiàn)貨波動大于期貨波動。

（五）不同模型下白銀套保有效性比較及模型準確性檢驗

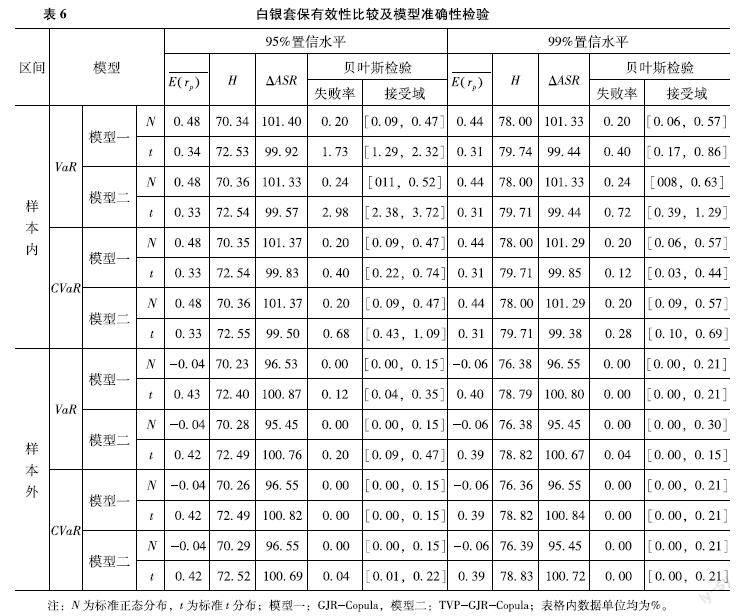
在得出不同模型下白銀套期保值比率后，本文對樣本內(nèi)不同模型不同分布和不同置信水平下的套保效果（套保有效性）進行對比分析。接著對樣本外數(shù)據(jù)用擬合得到的邊緣分布模型進行收益率和變動率預(yù)測并進行套保有效性檢驗，最后對VaR和CVaR模型準確性進行檢驗。結(jié)果如表6所示。

由表6可知，在樣本內(nèi)：

①套保組合的收益率較小，集中于03%～05%，接近完全套期保值，95%置信水平下套保組合的收益率要高于99%置信水平下套保組合的收益率；

②無論是基于VaR還是CVaR，動態(tài)TVP-GJR-Copula模型下的套保效果都要好于靜態(tài)GJR-Copula；

③在同模型和同分布情況下，套保有效性隨置信水平的上升而提高；

④在VaR或CVaR模型內(nèi)，t分布下的套保有效性要強于正態(tài)分布下的有效性，且基于CVaR模型的有效性也要高于VaR模型，動態(tài)TVP-GJR-t?Copula的套保效果最好；

⑤無論在何種模型、何種分布和置信水平下，修正的夏普比率變化率顯示，白銀現(xiàn)貨經(jīng)套保后的單位風險比較基準收益率較不套保時的收益率有大幅提高，同時套保有效性指標達到70%～80%，說明價格波動率均有不同程度的降低，也即價格風險都有所規(guī)避；

⑥貝葉斯檢驗結(jié)果顯示，失敗率落于接受域內(nèi)，說明VaR或CVaR模型是準確的，可以接受基于該模型得到的套保比率和套保有效性。在樣本外，雖然套保的組合收益率有所降低，但套保有效性與樣本內(nèi)的差異不大，且達到降低市場風險的功能，特別是t分布情況下風險降低程度最大。總體而言，本文所建立的套保模型在進行白銀套期保值操作時能最大限度地降低現(xiàn)貨市場風險，同時能取得最優(yōu)的套期保值效果。但與歐美成熟期貨市場80%的風險分散水平相比，我國期貨市場還有差距，期貨市場的套期保值功能有待發(fā)揮。

五、結(jié)語

本研究基于VaR和CVaR最優(yōu)套保比率模型視角，構(gòu)建了白銀現(xiàn)貨與期貨二元條件下的具有誤差修正項（基差變化）的GJR?Copula-N（t）模型，然后從靜態(tài)和動態(tài)兩個角度，選取上金所白銀延期和上期所主力合約數(shù)據(jù)估計了不同置信水平下的套保比率，并測算和比較了各種情況下樣本內(nèi)外套保有效性，得出以下結(jié)論：第一，白銀期現(xiàn)貨市場間具有相同變化特征和相同的影響因素，當期收益率會受上期收益率影響，即具有自相關(guān)性，且基差隨時間后移會對收益率產(chǎn)生正向效應(yīng)；t分布下白銀期現(xiàn)收益率波動存在明顯非對稱性和厚尾特征；同時，白銀期現(xiàn)貨市場是動態(tài)聯(lián)動性的內(nèi)部結(jié)構(gòu)，相關(guān)性是動態(tài)非線性變化的。第二，與傳統(tǒng)最小方差目標套保模型相比，基于VaR和CVaR的最優(yōu)套保比率模型在測算套保比率時考慮了“投機需求”部分，直接與套保者的風險態(tài)度相聯(lián)系，套保者可根據(jù)風險偏好選擇不同的套保策略，風險偏好型套保者可選擇置信水平低的套保比率，風險厭惡型套保者可選擇置信水平高的套保比率。第三，從估計的套保比率結(jié)果看，整體上動態(tài)TVP-GJR-Copula模型得到的套保比率大于靜態(tài)GJR-Copula模型；CVaR最小化目標套保策略下的套保比率高于VaR策略，且CVaR因量化超過VaR的損失，使計算得到的CVaR均值要大于VaR均值，是一種更為保守的風險度量工具。第四，從套保效果和檢驗結(jié)果看，在VaR或CVaR最小化目標框架下，套保有效性達到70%～80%。動態(tài)套保模型的套保效果要好于靜態(tài)模型；基于CVaR模型的有效性優(yōu)于VaR模型，且動態(tài)TVP-GJR-t?Copula的套保效果最好。另外，白銀現(xiàn)貨經(jīng)套期保值后，單位風險比較基準收益率較不套保時有大幅提高，價格波動率被熨平，市場風險能夠得到最大程度的降低。同時，貝葉斯檢驗結(jié)果顯示，失敗率落于接受域內(nèi)，說明VaR或CVaR模型是準確的，可接受基于該模型得到的套保比率和套保有效性。

鑒于以上研究結(jié)論，在新常態(tài)下特別是后疫情時代，白銀期現(xiàn)貨市場間的聯(lián)系愈發(fā)緊密，波動更為頻繁和劇烈，作為一種扮演重要角色的工業(yè)品和投資品，對套保者和投資者來說，選擇合適的套期工具熨平市場波動至關(guān)重要。為此，本文提出以下建議：

①要從風險管理的角度充分測算套保標的與所選套保工具間的波動率、殘差分布情況及相關(guān)性等，建立動態(tài)套保策略，避免偽套保導致風險敞口放大；

②投資者要根據(jù)自身風險厭惡程度、損失承受能力等采取適合的套期保值策略以取得最佳的套保效果；

③白銀市場發(fā)生急劇波動的行情已成常態(tài)，投資者應(yīng)更多關(guān)注套保期間的極值收益率變化對保證金的沖擊，并根據(jù)套保比率和預(yù)期動態(tài)調(diào)整自己的期現(xiàn)貨頭寸，并建立預(yù)警機制。

本文的研究仍存在一些不足之處。首先，本文設(shè)定期現(xiàn)貨殘差服從具有尾部對稱性的正態(tài)分布或t分布，但現(xiàn)實中資產(chǎn)還存在偏度風險、峰度風險和結(jié)構(gòu)突變等特征，不一定是較合適的模型；其次，我們在運用VaR或CVaR模型測算套保比率時考慮的是空頭套保情形，沒有驗證多頭套保情形，選取的樣本為滬銀30分鐘數(shù)據(jù)，且存在先分析后進行套保測算問題，是否適用其他市場的白銀品種或更長期間內(nèi)的情況，有待進一步驗證和研究；最后，本研究假設(shè)不存在增值稅稅率變化影響，忽略諸如傭金、手續(xù)費、倉儲費、保證金利息等交易費用等，而交易成本會影響套保方法的選擇、套保比率的確定和套保有效性的衡量。

參考文獻

［1］遲國泰，趙光軍，楊中原基于CVaR的期貨最優(yōu)套期保值比率模型及應(yīng)用［J］.系統(tǒng)管理學報，2009，18（1）：27-33

［2］JOHNSON?L?LThe?theory?of?hedging?and?speculation?in?commodity?futures［J］.The?Review?of?Economic?Studies，1960，27（3）：139-151

［3］STEIN?J?LThe?simultaneous?determination?of?spot?and?futures?prices［J］.American?Economic?Review，1961（51）：1012-1025

［4］KOLB?R?W，OKUNEV?JUtility?Maximizing?Hedge?Ratios?in?the?Extended?Mean-Gini?Framework［J］.The?Journal?of?Futures?Markets，1993，13（6）：597-609

［5］HSIN?C?W，KUO?J，LEE?C?FA?new?measure?to?compare?the?hedging?effectiveness?of?foreign?currency?futures?verus?options［J］.The?Journal?of?Futures?Markets，1994，14（6）：685-707

［6］CHEN?S?S，LEE?C?F，SHRESTHA?KOn?a?mean-generalized?Semivariance?approach?to?determining?the?hedge?ratio［J］.Journal?of?Futures?Markets，2001，21（6）：581-598

［7］黃長征期貨套期保值決策模型研究［J］.數(shù)量經(jīng)濟與技術(shù)經(jīng)濟研究，2004（7）：96-102

［8］EDERINGTON?L?HThe?hedging?performance?of?the?new?futures?markets［J］.The?Journal?of?Finance，1979，34（1）：157-170

［9］吳文峰，劉太陽，吳沖鋒上海與倫敦期銅市場之間的波動溢出效應(yīng)研究［J］.管理工程學報，2007（3）：111-115

［10］GHOSH?AHedging?with?Stock?Index?Futures?：Estimation?and?Forecasting?with?Error?Correction?Model［J］.The?Journal?of?Futures?Markets（1986-1998），1993，13（7）：743-752.

［11］林孝貴期貨套期保值最大概率與最小風險分析［J］.數(shù)學的認識與實踐，2004（5）：24-29

［12］王玉剛，遲國泰，吳珊珊基于非線性相關(guān)的最小方差套期保值比率研究［J］.價值工程，2006（10）：154-157

［13］MATHEW?K?H，?HOLTHAUSEN?D?M?;JrA?simple?multiperiod?minimum?risk?hedge?model［J］.American?Journal?of?Agricultural?Economics，1991，73（4）：1020-1026

［14］HSU?C?C，TSENG?C?P，WANG?Y?HDynamic?Hedging?with?Futures：a?Copula-based?GARCH?Model［J］.The?Journal?of?Futures?Markets，2008，28（11）：1095-1116

［15］LAI?Y?H，CHEN?C?W?S，?GERLACH?ROptimal?Dynamic?Hedging?via?Copula-Threshold-GARCH?modes［J］.Mathematics?and?Computers?in?Simulation，2009，79（8）：2609-2624

［16］謝赤，余聰，羅長青，等基于MRS?Copula-GJR-Skewed-t模型的股指期貨套期保值研究［J］.系統(tǒng)工程學報，2013，28（1）：83-93

［17］LIEN?D，TSE??Y?K?Hedging?time-varying?down?side?risk?［J］.The?Journal?of?Futures?Markets，1998，18（6）：705-722

［18］陳蓉，蔡宗武，陳妙瓊最小下偏矩套期保值比率估計研究——基于混合copula方法［J］.廈門大學學報（哲學社會科學版）.2009（3）：34-40，53

［19］周亮球，謝赤商業(yè)銀行外匯套期保值研究——一個基于時變Clayton?Copula-LPM模型的實證［J］.南大商學評論，?2013，10（4）：72-88

［20］HUNG?J?C，CHIU?C?L，?LEE?M?CHedging?with?zero-value?at?risk?hedge?ratio［J］.Applied?Financial?Economics，2006，16（3）：259-269

［21］顧能柱基于CVaR約束的期貨套期保值模型構(gòu)建［J］.財會月刊，2008（11）：25-26

［22］謝赤，屈敏，王綱金基于M-Copula-GJR-VaR模型的黃金市場最優(yōu)套期保值比率研究［J］.管理科學，?2013，26（2）：90-99

［23］王炎VaR和CVaR方法下最優(yōu)套期保值的選擇研究［D］.南京：南京財經(jīng)大學，2008

［24］GLOSTEN L?R，JAGANNATHAN?R，RUNKLE?D?E.Relationship?between?the?Expeected?Value?and?the?Volatility?of?the?Nominal?Excess?Return?on?StocksJournal?of?Finance，1993，48（5）：1779-1801

［25］PATTON?A?JModeling?asymmetric?exchange?rate?dependence［J］.?International?Economic?Review，2006，47（2）：527-556

［26］吳筱菲，朱淑珍，白正午基于MRS-SJC-Copula模型對A股與港股的動態(tài)聯(lián)動性研究［J］.運籌與管理，2020，29（1）：176-184

［27］楊永愉，丁進，楊凡VaR模型后驗測試的貝葉斯方法［J］.統(tǒng)計與決策，2005（2）：4-7

［28］王向翠，董佳慧VaR準確性檢驗的貝葉斯方法［J］.企業(yè)技術(shù)開發(fā)，?2009，28（10）：44-45