跳擴散模型下具有情緒的期權定價

摘?要：在跳擴散模型下考慮具有股票情緒和期權情緒的期權定價模型。假設標的資產跳躍的到達服從泊松過程，跳躍的幅度服從正態過程，且股票情緒和期權情緒都服從O-U過程。對所構建的模型，求得了歐式期權定價解析式。利用上證50ETF看漲期權數據進行實證研究，通過與幾何布朗運動模型，帶跳的幾何布朗運動模型和Heston模型進行對比，發現在平穩樣本時期、波動樣本時期和全樣本時期，文章所提模型在上證50ETF看漲期權價格的擬合和預測誤差均是最小的，以及在隱含波動率的擬合和預測誤差也是最小的，表明文章的模型在平穩時期，非平穩時期以及既有平穩時期又非平穩時期，期權價格的擬合和預測能力以及隱含波動率的擬合和預測能力都是優于對比模型的。

關鍵詞：期權定價；股票情緒；期權情緒；隱含波動率

作者簡介：呂建平，博士，講師，研究方向為金融工程與風險管理、資產定價。

一、引言

上證50ETF期權自發布以來，其價格走勢一直受到許多投資者的關注。期權價格是期權理論的核心內容，想要得到更準確的期權價格，則期權標的資產價格動態的合理刻畫很關鍵。在傳統的期權定價研究中，假定投資者都是理性的和風險中性的，標的股票的期望增長率和貼現率都等于無風險利率（Black和Scholes，1973；Rodriguez，?2002；Guo和Yuan，2014）。然而，Klemkosky和Resnick?（1979）和Rubinstein?（1985）的研究發現，傳統期權定價模型得到的期權價格與實際市場的期權價格存在較大偏差。為了改進傳統期權定價模型所存在的缺陷，研究者們試圖修改模型的假設前提，但修正后的模型對于存在的許多問題仍然無法解決。究其原因是這些模型仍然保留著“所有參與者都是理性的”的假定，基于在完全理性的條件下建立的模型與市場的實際情況是非常不符的。Simon?（1955）認為投資者不是完全理性的，當然也不是完全不理性的，因此提出了有限理性的假定，他認為投資者在做決策時除了獲得的信息之外，教育背景以及自身的學識和計算能力等都會影響其判斷與決策，因此投資者并不會像假設中所提到的那樣是完全理性的，而是容易受到影響或者產生某種認知偏差。在期權市場中，投資者是非理性的和風險厭惡的。

文獻表明在期權定價模型中考慮投資者情緒使得期權定價的預測結果更貼近實際金融市場。一些實證結果表明，來自期權市場和股票市場的情緒因子對期權定價都有著重要的系統性影響。股票情緒是投資者對未來股票價格分布信念的總誤差。期權情緒是投資者對未來期權價格分布信念的總誤差。Han?（2008）發現期權價格受到股票情緒的影響，股票情緒的各種指標與指數期權收益顯著相關。Sheu和Wei?（2011）使用期貨波動率、期權波動率指數、看跌期權交易量和未平倉利率等作為期權情緒來研究這種情緒是如何影響期權價格和收益的波動。股票投資者不同于期權投資者，股票市場的重要參與者是個人投資者，而期權投資者的機構投資者占比較高。因此，這兩組投資者可能會受到不同的情緒影響。期權的價格在受到期權市場影響的同時也受到標的股票市場的影響，需要綜合考慮兩個市場的情況才能更加完善地分析期權價格。所以，文章將股票情緒和期權情緒納入期權定價模型。與以往文獻的不同之處在于文章考慮股票情緒和期權情緒的變化都由兩個O-U過程進行刻畫，并利用上證50ETF期權數據對文章模型與經典模型進行實證研究。

二、理論模型的構建

（一）股票情緒

Delong等（1990）在股票價格模型中首次考慮了投資情緒這一因素，發現積極的投資者情緒會推動股票價格上漲。Swaminathan（1996）認為投資者情緒可用來預測未來股票收益率，發現當投資者樂觀時股票價格上漲，收益率增加。Brown和Cliff（2004）、王美今和孫建軍（2004）發現投資者情緒變化與股市收益率具有很強正相關性。

假設標的股票的理性價格為P（t），令X（t）=ln（P（t）），那么標的股票價格的對數X（t）滿足如下

dX（t）=μs-12σ2-λm1dt+σdB（t）+dJ（t）（1）

其中dJ（t）=ε（t）dN（t），N（t）是具有固定跳強度λ的泊松過程。ε（t）服從對數正態分布，?即，

ln（1+ε（t））～N（μ，δ2），?那么m1=eu+12δ2-1。μs，σ分別表示標的價格理性漂移率和波動率，f（S1（t））=aS1（t）?，其中S1（t）為股票情緒，?α＞0為情緒敏感系數。此外，?期權情緒為g（S2（t））=bS2（t），b＜0為情緒敏感系數。情緒Si（t）滿足如下

dSi（t）=-kiSi（t）dt+σidBi（t），i=1，2（2）

其中，ki，σi分別表示情緒均值回復系數和波動率。此外，dB（t）dB1（t）=ρdt，B2（t）獨立于任何布朗運動。如果投資者具有情緒的，?那么在進行股票交易時，?對未來股票價格的判斷是隨機變量

lnF（t）=X（t）+f（S1（t））（3）

（二）期權情緒

傳統的期權定價模型都假設投資者是風險中性的，任何投資的期望回報是無風險利率。然而，根據Warner和Pleeter?（2001），Kable和Glimcher（2007），折現率是受主觀觀點影響的。Lawrence等（2007）發現情緒影響期望折現率，投資者情緒越高，折現率越低，?Yang等（2016）也發現類似結果。因此，到期時間為T，在時間t受情緒影響的歐式看漲期權價格為

U（t）=［e-（r（T-t）+g（S2（T-t）））C（T）］（4）

其中，r是看漲期權的期望回報率，?ɡ（S2（t））是看漲期權情緒，C（T）=（F（T）-K）+。

三、期權定價

這一節來求具有執行價格為K，到期時間為T在時間0的歐式期權價格的解析式。

命題1?假設標的價格滿足（1），那么具有執行價格為K，到期時間為T在時間0的歐式期權價格為?

U=［e-（rT+ɡ（S2（T）））C（T）］

=C1C2

（5）

其中，?C1，C2滿足

C1=em+12N（d1）-KN（d2）（6）

C2=e-（r*（T-t）+bS2（0）e-x2（T-t））+b2σ224x2（1-e-222（T-t））（7）

和

d1=-lnK+mv+v，

d2=-lnK+mv+v

證明：?因為B2（t）獨立于任何布朗運動，?并與跳過程相互獨立，?因此

U=［e-（rT+ɡ（S2（T）））］［C（T）］（8）

其中

［C（T）］=［（F（T）-K）+］

=∫∞K（u-K）dH（u）（9）

式（8）中H（u）是受情緒影響的標的股票價格F（T）的分布函數，u∈［0，∞）。首先，計算［C（T）］，

［lnF（T）］=X（0）+（μs-12σ2）T+αS1（0）e-k1T，

Var［lnF（T）］=σ2T+α2σ212k1（1-e-2k1T）+2αρσσ1k1（1-e-k1T）

+λ（e2（μ+δ2）-2eμ+12δ2+1）T，

令m=［lnF（T）］，v=Var［lnF（T）］，并定義新的變量：

φ=lnF（T）-mυ，（10）

新的變量φ服從標準正態分布，?即，?均值為0，?方差為1?，?其概率密度函數p（φ）為

p（φ）=12πe-φ22

（11）

通過式（8）、式（9）和式（10）?得到

［C（T）］=∫∞K（u-K）dH（u）

=∫∞lnK-m∞（evφ+m-K）p（φ）dφ

=∫∞lnK-mvevφ+mp（φ）dφ-K

∫∞lnK-mv

P（φ）dφ（12）

因為

evφ+mp（φ）=12πe-φ2+2vφ+2m2

=em+v222πe-（φ-v）22

=em+v22p（φ-v）（13）

把式（12）代入式（11）得到?

［C（T）］=em+v22∫∞lnK-mv?ρ（φ-v）dφ

-K∫∞lnK-mv?ρ（φ）dφ（14）

令N（x）表示累積標準正態概率分布函數，?那么

1-NlnK-mv-v=N-lnK+mv+v，

1-NlnK-mv=N-lnK+mv（15）

通過式（14），式（13）變為

［C（T）］=em+v22N（d1）-KN（d2）.（16）

其中

d1=-lnK+mv+v，

d2=-lnK+mv

接下來計算

［e-（rT+ɡ（S2（T）））］

，?因為

［e-（rT+ɡ（S2（T）））］=e-（r*T+bS2（0）e-k2T）+b2σ224k2（1-e-2k2T）

（17）

然后通過（15）和（16），?最終求得歐式期權解析定價公式。

四、實證分析

這一節將基于文章所提模型，Heston模型，幾何布朗運動模型（BS模型）和帶泊松跳過程的幾何布朗運動模型（BSJ模型）進行期權價格擬合和預測以及隱含波動率的擬合和預測來評估文章模型與基準模型在相應擬合和預測方面的性能。其中Heston（1993）的模型滿足如下過程

dS（t）=μS（t）dt+v（t）S（t）dBs（t）

dv（t）=k（θ-v（t））dt+σvv（t）dBv（t）（18）

其中，?μ為期望回報率，v（t）為隨機波動率，?且Bs（t）和Bv（t）都是標準布朗運動，dBs（t）dBv（t）=ρ1dt。

（一）數據的選取與處理

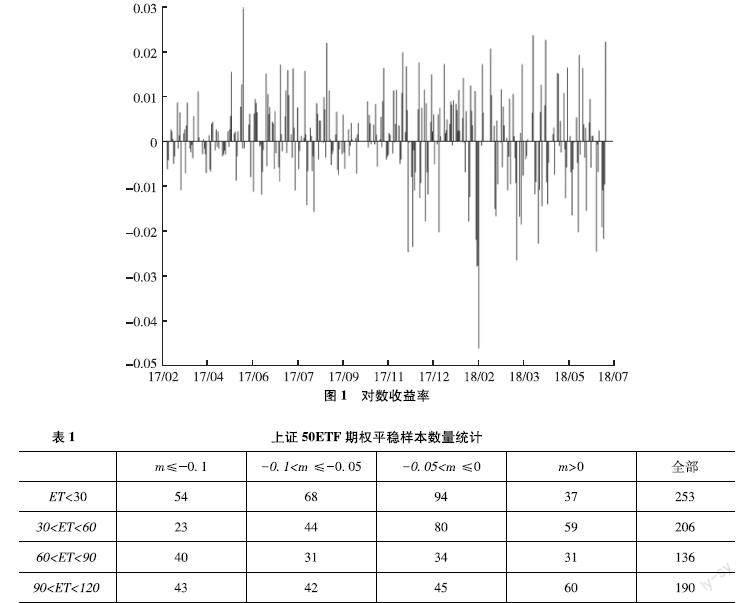
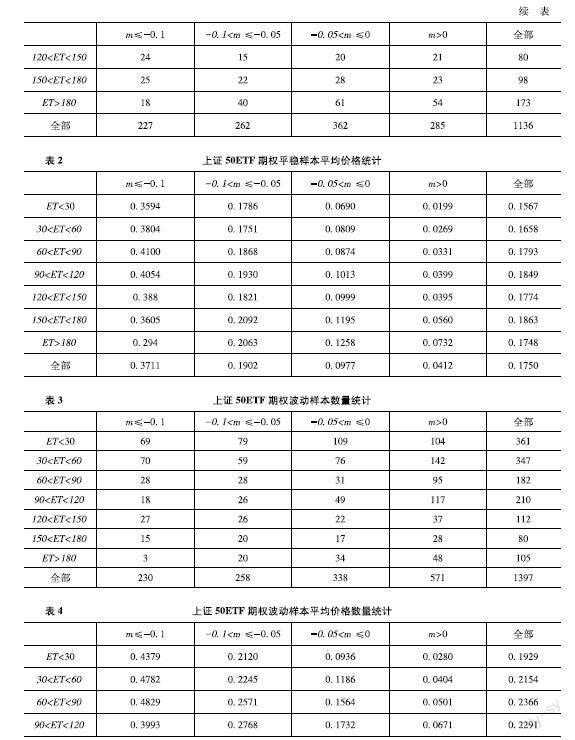
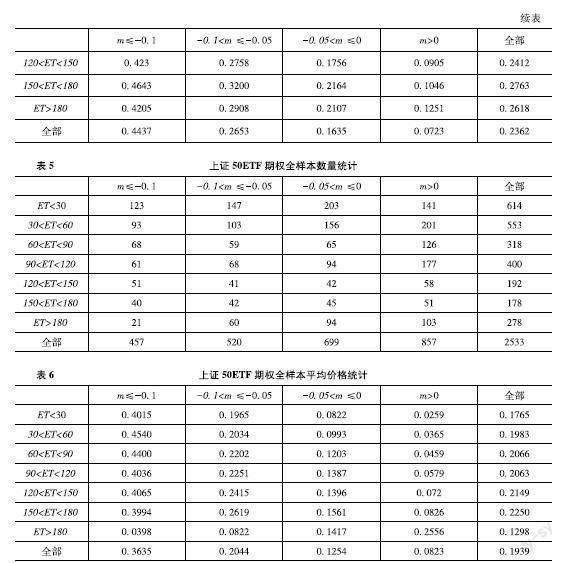
為了驗證文章的模型在歐式期權定價的有效性，本節通過真實的市場數據來進行檢驗，即考慮上證50ETF看漲期權數據作為實證研究對象，該期權數據來源于同花順數據庫。選取一年期中債國債即期收益率作為理性期望回報率，數據來源于中國債券信息網。圖1顯示的是上證50ETF在2017年3月1日至2018年6月29日的對數收益率，從圖1可看出對數收益率在2017?年3月至2017?年10月相對平穩，而在2017?年11月至2018年6月波動的幅度較大，波動幅度大與中美貿易戰持續升級以及人民幣持續貶值有關。文章選取上證50ETF看漲期權2017年3月至2017年10月每周三的期權數據作為平穩樣本數據，上證50ETF看漲期權2017年11月至2018年6月每周三的期權數據作為波動樣本數據。文章選取上證50ETF看漲期權數據2017年3月至2018年6月每周三期權數據作為全樣本數據。在以上樣本都用相應每周四上證50ETF看漲期權數據來評估模型的預測能力。在對模型參數進行較準前，首先需要對期權數據進行篩選，剔除期權價格數據缺失以及到期日小于7天。其次剔除不滿足期權價格隨執行價格增大而遞減的期權價格數據。最后還要剔除深度虛值中期權價格接近0的期權數據。篩選后，文章得到期權全樣本數據2533個。表1至表6展示了樣本時期內，不同到期時間和價值狀態所對應的上證50ETF看漲期權數量和平均價格，其中m?=?ln（K/F（0））表示期權的價值狀態，ET表示剩余到期時間。對于看漲期權來說，m?<?0，m?=?0和m?>?0分別表示實值期權，平值期權和虛值期權。從表5可知，上證50ETF看漲期權數量主要集中于到期時間120天以內，其中到期時間在60天以內的期權數量接近一半。從表6可知，到期時間在120天至150天，以及150至180?天之間期權的平均價格較高。

（二）模型校準目標和擬合、預測指標

模型校準目標函數采用如下誤差平方和（Sum?of?Squared?Error，?SSE），

SSE=∑Nj=1（CModelKj，T-CMarketKj，T）2（19）

其中，CModelKj，Tj和

CMarketKj，Tj

分別表示行權價為Kj?到期日為Tj同一期權的模型報價和市場報價。模型校準以式（18）中誤差平方和最小化為目標。

模型校準效果的評價指標主要有平均絕對誤差（Mean?Absolute?Error，?MAE）、?平均相對誤差（Mean?Relative?Error，?MRE）和均方根誤差（Root?Mean?Squared?Error，?RMSE），?其分別定義為

MAE=1N∑Nj=1CModelKj，Tj-

CMarkerKj，Tj

（20）

MRE=1N∑Nj=1CModelKj，Tj-

CMarketKj，Tj

CMarktTj，Kj

（21）

和

RMSE=

1N∑Nj=1（CModelTj，Kj-CMarketKj，Tj）2

（22）

平均絕對誤差越小，模型價格與期權價格越接近，期權定價模型的校準效果就越好。而平均相對誤差能夠消除不同大小期權價格的誤差相加所存在的量綱差異問題，從而對期權校準評判更為合理。本文采用平均絕對誤差、平均相對誤差和均方根誤差來衡量期權定價模型對期權市場價格的預測能力。

（三）參數校準及模型擬合和預測期權價格的比較

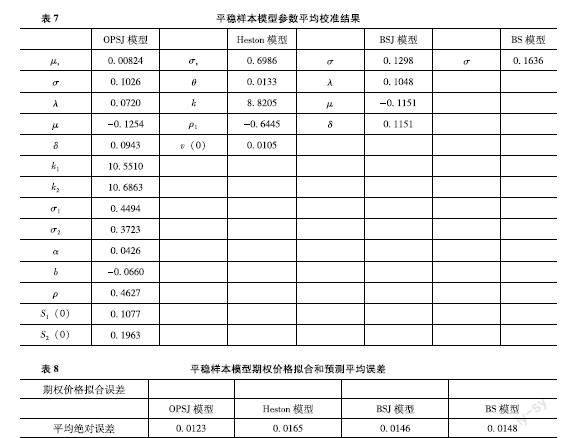
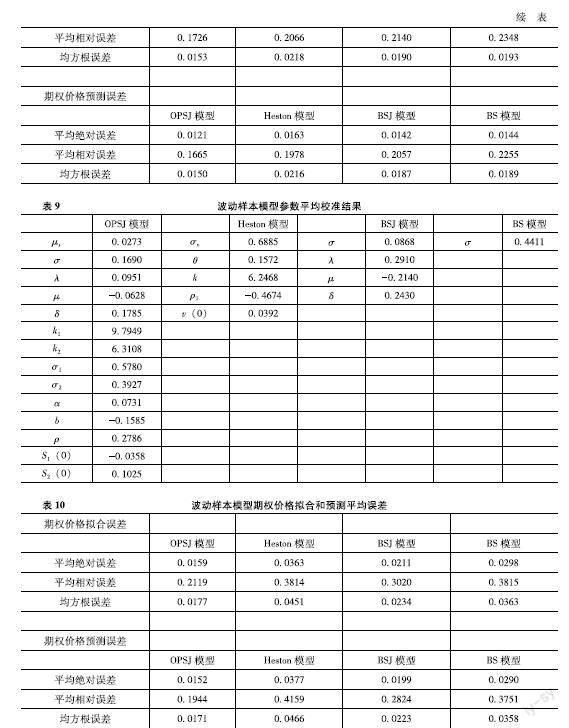
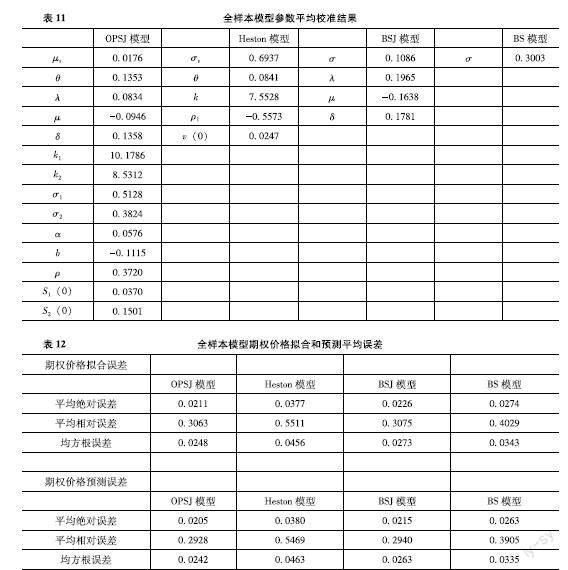
利用每周三的期權數據對模型參數進行校準，表7、表9和表11分別展示了在平穩樣本時期、波動樣本時期和全樣本時期內OPSJ模型、Heston模型、BSJ模型和BS模型參數平均校準結果。表8、表10和表12分別展示了三個模型在平穩樣本時期、波動樣本時期和全樣本時期內期權價格擬合和預測的平均絕對誤差、平均相對誤差和均方根誤差。從表8可知，OPSJ模型在平穩樣本時期內期權價格的擬合和預測的平均絕對誤差、平均相對誤差和均方根誤差在三個模型中是最小的，這說明OPSJ模型在平穩樣本時期內期權價格的擬合和預測上表現的最好。從表10可知，OPSJ模型在波動樣本時期內期權價格的擬合和預測的平均絕對誤差、平均相對誤差和均方根誤差在三個模型中的誤差值是最小的，這說明OPSJ模型在波動樣本時期內期權價格的擬合和預測上表現的最優。從表12可知，OPSJ模型在全樣本時期內期權價格的擬合和預測的平均絕對誤差、平均相對誤差和均方根誤差在三個模型中也是最小的，這說明OPSJ模型在全樣本時期內期權價格的擬合和預測上表現最佳。

（四）模型擬合和預測隱含波動率的比較

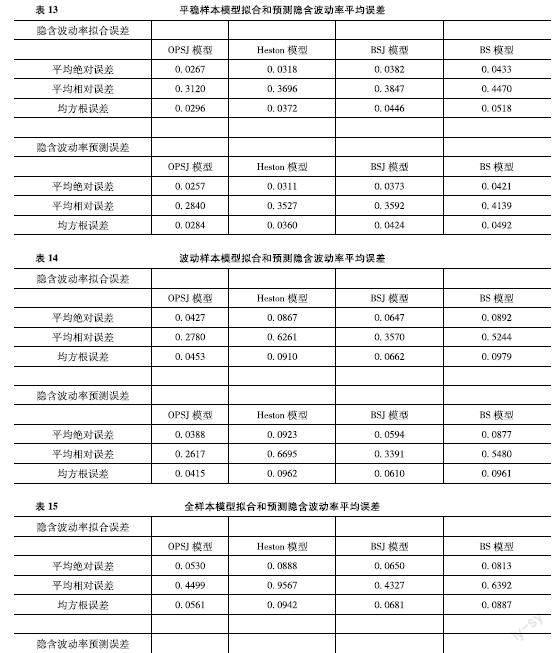
這一節將通過上節在平穩樣本時期，波動樣本時期和全樣本時期內OPSJ模型、Heston模型、BSJ模型和BS模型所得的校準參數來擬合和預測各自模型的隱含波動率，并與真實市場的隱含波動率進行比較，同樣通過平均絕對誤差、平均相對誤差和均方根誤差來評估期權定價模型對期權市場隱含波動率的擬合和預測能力。表13、表14和表15分別表示在平穩樣本時期、波動樣本時期和全樣本時期內OPSJ模型、Heston模型、BSJ模型和BS模型的隱含波動率擬合和預測的平均誤差。表13可看出，在平穩樣本時期內，OPSJ模型擬合和預測隱含波動率的平均誤差在四個模型中是最小的，表明OPSJ模型在平穩樣本時期內擬合隱含波動率的能力是優于對比模型的。表14可看出，在波動樣本時期內，OPSJ模型擬合和預測隱含波動率的平均誤差在四個模型中的誤差值是最小的，表明OPSJ模型在波動樣本時期內擬合和預測隱含波動率的能力是好于其他三個模型的。表15可看出，在全樣本時期內，OPSJ模型擬合和預測隱含波動率的平均誤差在四個模型中也是最小的，表明OPSJ模型在全樣本時期內擬合和預測隱含波動率的能力也是優于對比模型的。

五、結論

在傳統的期權定價模型中考慮股票情緒與期權情緒，且情緒都服從O-U過程，標的資產跳躍的到達服從泊松過程，跳躍的大小服從正態分布，針對該模型求得了歐式期權定價解析式。利用2017年3月至2018?年6月上證50ETF期權數據進行實證研究，通過與幾何布朗運動模型，帶跳的幾何布朗運動模型和Heston模型進行對比發現，在平穩樣本時期、波動樣本時期和全樣本時期，OPSJ模型在上證50ETF看漲期權價格的擬合和預測誤差均是最小的，以及在隱含波動率的擬合和預測誤差也是最小的，表明OPSJ模型在平穩時期、非平穩時期以及既有平穩時期又有非平穩時期，期權價格的擬合和預測能力都優于對比模型，并且在隱含波動率的擬合和預測能力也是優于對比模型。?

參考文獻

[1]BLACK?F，?SCHOLES?M?The?pricing?of?options?and?corporate?liabilities[J].?Journal?of?Political?Economy，?1973，?81（3）：?637-654

[2]RODRIGUEZ?R?J?Lognormal?option?pricing?for?arbitrary?underlying?assets：?a?synthesis[J].?The?Quarterly?Review?of?Economics?and?Finance，?2002，?42（3）：?577-586

[3]?GUO?Z?D，?YUAN?H?J?Pricing?European?option?under?the?time-changed?mixed?Brownian?fractional?Brownian?model[J].?Physica?A：?Statistical?Mechanics?and?its?Applications，?2014，40（C）：73-79

[4]?KLEMKOSKY?R?C，?RESNICK?B?G?Put-call?parity?and?marketefficiency[J].?The?Journal?of?Finance，?1979，?34（5）：?1141-1155

[5]?RUBINSTEIN?M?Nonparametric?tests?of?alternative?option?pricing?models?using?all?reported?trades?and?quotes?on?the?30?most?active?CBOE?option&nbsp;classes?from?August?23，?1976?through?August?31，?1978[J].?The?Journal?of?Finance，?1985，?40（2）：?455-480

[6]?SIMON?H?A?A?behavioral?model?of?rationalchoice[J].?The?Quarterly?Journal?of?Economics，?1955，?69（1）：?99-118

[7]?POTESHMAN?A?MUnderreaction，overreaction，and?increasing?misreaction?to?information?in?the?options?market[J].?Journal?of?Finance，?2001，?56（3）：?851-876

[8]?BAUER?R，?COSEMANS?M，?EICHHOLTZ?P?Option?trading?and?individual?investorperformance[J].?Journal?of?Banking?and?Finance，?2009，?33（4）：?731-746

[9]?SIDDIQI?H?Thinking?by?analogy?and?optionprices[J].SSRN?Electronic?Journal，?2011：?1905384

[10]JACKWERTH?J?C，?realized?returns?Recovering?probability?distributions?from?optionprices[J].?Journal?of?Finance，?1996，?51（5）：?1611-1631

[11]?JACKWERTH?J?C?Recovering?risk?aversion?from?option?prices?and?realized?returns[J].The?Review?of?Financial?Studies，?2000，?13（2）：?433-451

[12]林焰，楊建輝考慮投資者情緒的GARCH-改進神經網絡期權定價模型[J].系統管理學報，2018，?27（5）：?863-871，880

[13]劉桂芳，徐維軍，黃靜龍，等考慮公司信息披露情緒的歐式脆弱期權定價[J].運籌與管理，2021，30（9）：164-171

[14]?HAN?B?Investor?sentiment?and?option?prices[J].?The?Review?of?Financial?Studies，?2008，?21（1）：?387-414

[15]?SHEU?H?J，?WEI?Y?COptions?trading?based?on?the?forecasting?of?volatility?direction?with?the?incorporation?of?investor?sentiment[J].?Emerging?Markets?Finance?and?Trade，?2011，?47（2）：?31-47

[16]?DELONG?J?B，?SHLEIFER?A，?SUMMERS?L?H，?et?al?Noise?trader?risk?in?financialmarkets[J].?Journal?of?Political?Economy，?1990，?98（4）：?703-738

[17]?SWAMINATHAN?B?Time-varying?expected?small?firm?returns?and?closed-end?fund?discounts[J].?Review?of?Financial?Studies，?1996，?9（3）：?845-887

[18]?BROWN?G?W，?CLIFF?M?T?Investor?sentiment?and?the?near-term?stockmarket[J].?Journal?of?Empirical?Finance，?2004，?11（1）：?1-27

[19]王美今，?孫建軍?中國股市收益、收益波動與投資者情緒[J].?經濟研究，?2004?（10）：?75-83

[20]?WARNER?J?T，?Pleeter?S?The?personal?discount?rate：?evidence?from?military?downsizing?programs[J].The??American?Economic?Review，?2001，?91（1）：?33-53

[21]?KABLE?J??W，?GLIMCHER?P?W?The?neural?correlates?of?subjective?value?during?intertemporal?choice[J].?Nature?Neuroscience，?2007，?10（12）：?1625-1633

[22]?LAWRENCE?E?R，?MCCABE?G，?PRAKASH?A?J?Answering?financial?anomalies：?Sentiment?based?stock?pricing[J].?The?Journal?of?Behavioral?Finance，?2007，?8（3）：?161-171

[23]?YANG?C，?GAO?B，?YANG?J?Option?pricing?model?with?sentiment[J].?Review?of?Derivatives?Research，?2016，?19（2）：?147-164

[24]?HESTON?S?L?A?closed-form?solution?for?options?with?stochastic?volatility?with?applications?to?bond?and?currencyoptions[J].?The?Review?of?Financial?Studies，?1993，?6（2）：?327-343

Option?pricing?with?sentiment?under?the?jump-diffusion?model

LYU?Jianping

（Economic?College，?Hunan?Agricultural?University，?Changsha??410128，?China）

Abstract：

The?option?pricing?with?stock?sentiment?and?option?sentiment?under?jump?diffusion?model?is?considered

Assume?that?the?arrival?of?the?underlying?asset?jump?follows?a?Poisson?process，?the?jump?amplitude?follows?a?normal?process，?and?the?stock?sentiment?and?option?sentiment?follow?an?OU?process?The?analytical?formula?of?European?option?pricing?is?obtained?Using?the?50ETF?call?option?data?of?Shanghai?Stock?Exchange?for?empirical?research，?by?comparing?with?geometric?Brownian?motion?model，?geometric?Brownian?motion?model?with?jump?and?Heston?model，?it?is?found?that?in?the?period?of?stable?sample，?the?period?of?fluctuation?sample?and?the?period?of?full?sample，?the?fitting?and?prediction?errors?of?the?model?are?the?smallest?in?the?50ETF?call?option?price?of?Shanghai?Stock?Exchange，?and?the?fitting?and?prediction?errors?in?the?implied?volatility?are?also?the?smallest?It?shows?that?the?proposed?model?is?superior?to?the?comparison?model?in?terms?of?fitting?and?forecasting?ability?of?option?price?and?implied?volatility?in?stable?period，?non-stationary?period?and?both?stable?and?non-stationary?periods

Keywords：Option?Pricing;?Stock?Sentiment;?Option?Sentiment;?Implied?Volatility