數學成績和專業課成績的相關性分析

付政慶，郭蘭蘭，馬康楠

（1．山東科技大學數學與系統科學學院 山東 青島 266590；（2．山東科技大學機械電子工程學院 山東 青島 266590）

在現代社會中，數學和專業技能都被認為是非常重要的素質。大學數學課程是高校大學生極其重要的公共基礎課，對大學生可持續發展能力的培養有著其他學科無法比擬的重要作用。數學成績與專業課成績的相關性需要深入研究。

多元統計分析是一種研究多個變量之間關系的方法，廣泛應用于各個領域的數據分析。現代教學管理中也會產生大量的教學數據，大數據的分析與學習可以用來對學生行為進行早期干預，輔助教師開展教學[1]。如李靜、寧勤等應用因子分析對學生成績進行綜合評價并與平均成績法對比分析[2-3]；江志冬等采用多元統計分析方法，對學生學習成績進行分析與研究，分析了成績在性別、班級維度上的差異[4]。Abdelhadi Abdelhakim 用多元統計的方法研究了醫師的學習風格和趨勢[5]。

1 研究對象和方法

本文選擇某高校測控技術與儀器專業的大學生作為研究對象，收集其綜合測評的專業課成績和數學成績作為此次數據樣本進行分析和研究。同時，還需收集其他可能影響結果的因素，如是否輟學、掛科補考等。

針對收集到的數據，采用統計方法進行數據清洗、篩選和分類，對數學成績進行學分加權處理。主要采用主成分分析、因子分析、回歸分析等方法，利用SPSS 軟件進行數據處理[6]。

檢驗數學成績在不同專業中是否對專業課成績有顯著影響，對相關性進行深入探究，并嘗試找到影響這種關系的因素，旨在為學校教育教學提供一定的依據和理論支持。

2 數據分析過程

2.1 KMO 度量標準和巴特利特檢驗

KMO檢驗系數是一種衡量數據樣本的結構效度的度量標準。KMO 值越接近1，變量間的相關性越強，越適合做因子分析。巴特利特球體檢驗的P值<0.05 時，數據樣本的結構效度非常好，進行因子分析能得到較好的結果。

將測控技術與儀器專業的數據樣本通過SPSS軟件分析后，由表1 測控技術與儀器的KMO 檢驗和巴特利特檢驗可知測控技術與儀器的KMO 統計量為0.875，并且P值為0.000，故該數據非常適合進行因子分析和主成分分析。

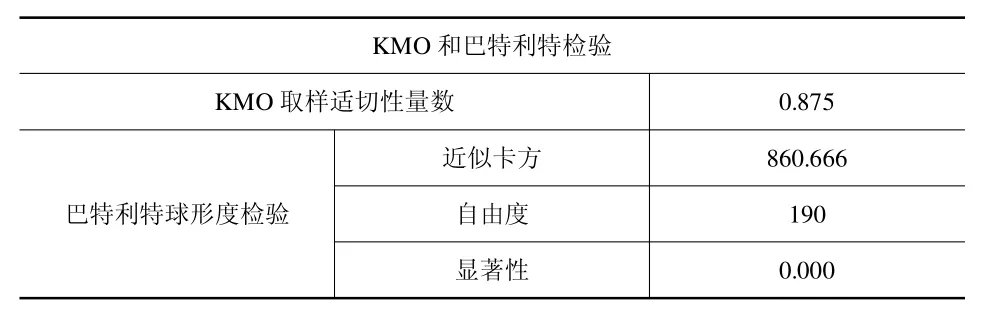
表1 測控技術與儀器的KMO 和巴特利特檢驗

2.2 公因子的選取

提取值表示每個變量被公因子表達的多少，一般認為，大于0.7 就說明變量被公因子很好地表達。

由表2 測控技術與儀器的公因子方差可以看出計算機數字控制技術、信號與系統、電路基礎、精密機械設計基礎、自動控制原理、制圖基礎（A）、中國近現代史綱要、思想道德修養與法律基礎、模擬電子技術、工程光學基礎、誤差與數據處理、毛澤東思想和中國特色社會主義理論體系概論、傳感器與檢測技術、大學英語（A）（2—2）、大學英語（A）（2—1）變量能被公因子很好地表達。由表3 測控技術與儀器的總方差解釋可知基于特征值大于1，提取4 個因子后，4 個因子共同解釋了原有變量的71.503%。

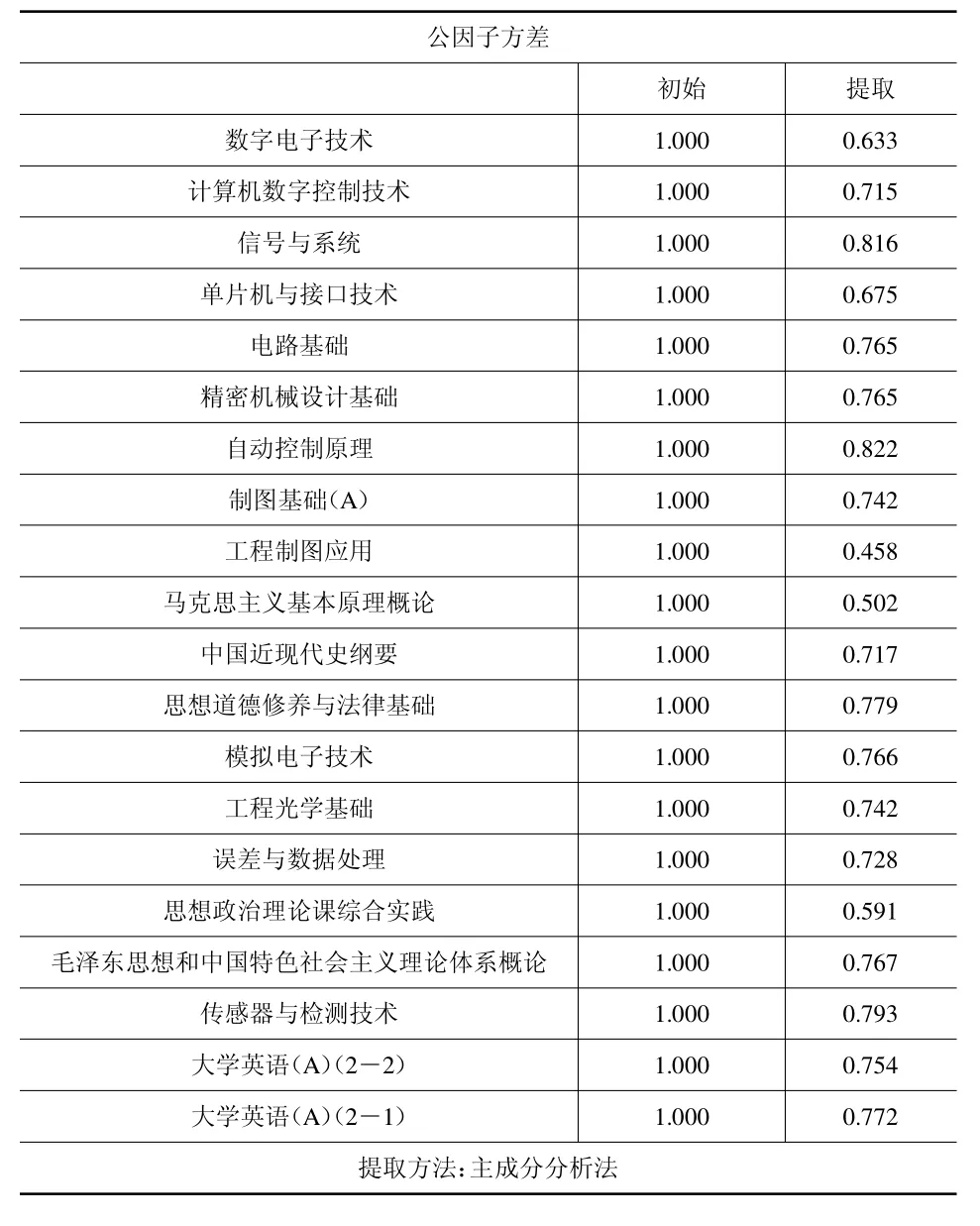
表2 測控技術與儀器的公因子方差

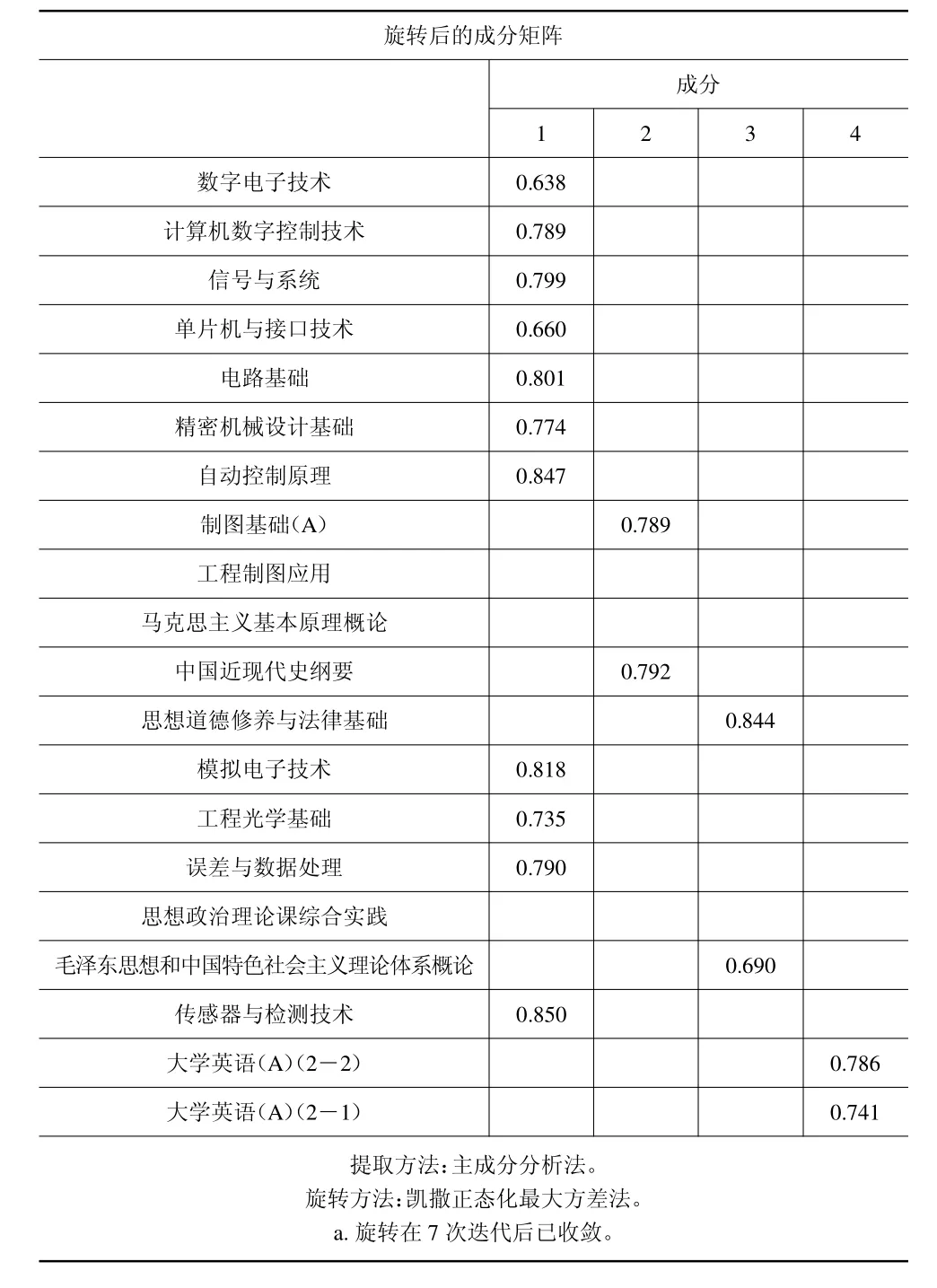
表3 測控技術與儀器的旋轉后的成分矩陣

2.3 公因子解釋

由表3 旋轉后的成分矩陣可知，數字電子技術、計算機數字控制技術、信號與系統、單片機與接口技術、電路基礎、精密機械設計基礎、自動控制原理，位于第一個因子上有較高的載荷，第一個因子主要解釋這幾個數據，我們稱之為核心課；制圖基礎（A）、中國近代史綱要位于第二個因子上有較高的載荷，第二個因子主要解釋這幾個數據，我們稱之為基礎課；思想道德修養與法律基礎、毛澤東思想和中國特色社會主義理論體系概論，位于第三個因子上有較高的載荷，第三個因子主要解釋這幾個數據，我們稱之為思想課；大學英語(A）（2—1）、大學英語（A）（2—2），位于第四個因子上有較高的載荷，第四個因子主要解釋這幾個數據，我們稱之為外語課。

由表4 可以得到的得分表達式為

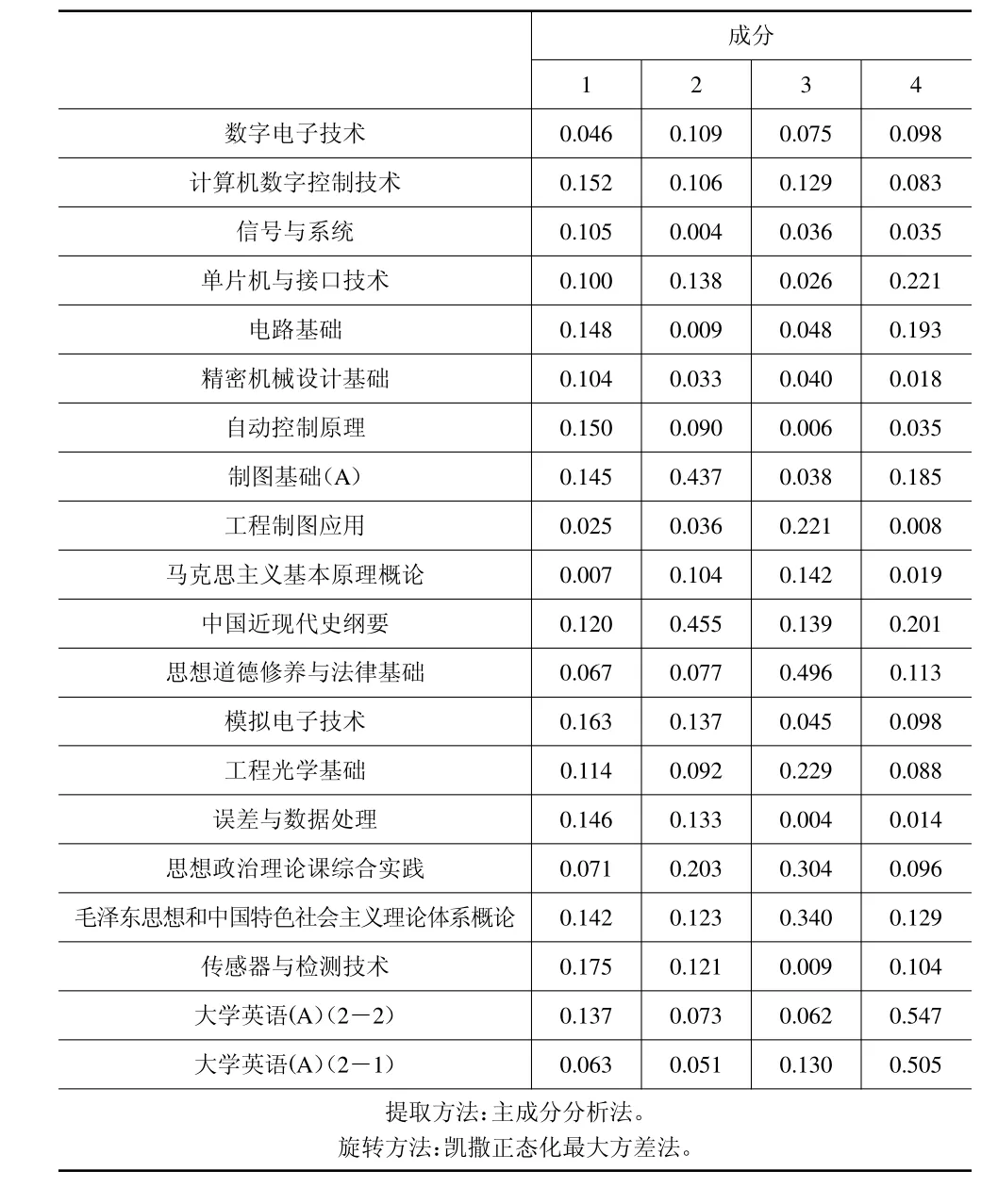
表4 測控技術與儀器的成分得分系數矩陣

式中：F1、F2、F3、F4分別是核心課、基礎課、思想課、外語課。可以看出，核心課在專業課中成績占比最大，外語課在該專業只開設了兩個學期只需淺學，所以在專業課中成績占比最小。我們通過F來得到專業課成績。然后我們用經過主成分分析和因子分析之后得到的測控技術與儀器專業的專業課成績做出線性回歸分析圖。

由圖1 可以看出，測控技術與儀器專業的數學成績與專業課成績具有較強的線性相關性，線性關系是正向的，測控技術與儀器的數學成績隨著專業課成績的增加而增加，專業課成績和數學成績的關系為1∶9.33。

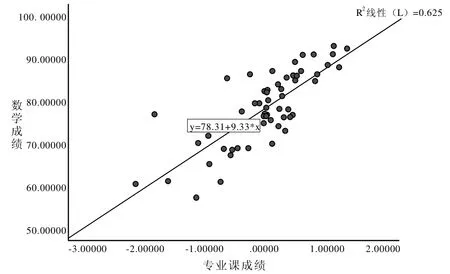
圖1 測控技術與儀器的線性回歸圖

3 結語

本文通過對專業成績和數學成績之間的相關性展開了探討和研究，利用主成分分析、因子分析和回歸分析對所得結果進行分析，測控技術與儀器專業的數學成績與專業課成績具有較強的線性相關性，線性關系是正向的，測控技術與儀器的數學成績隨著專業課成績的增加而增加，專業課成績和數學成績的關系為1∶9.33。專業課成績與數學成績的高低有著緊密的聯系，數學成績可以作為一個較好的參考因素，幫助評估不同專業背景下學生的表現。