基于擴張狀態觀測器的級聯無刷雙饋電機并網同步和發電魯棒預測電流控制

楊長山 張永昌 蔣 濤

基于擴張狀態觀測器的級聯無刷雙饋電機并網同步和發電魯棒預測電流控制

楊長山 張永昌 蔣 濤

（華北電力大學電氣與電子工程學院 北京 102206）

級聯無刷雙饋電機無需電刷和集電環，具有電流諧波小、維護成本低等優點，在風力發電等領域具有廣闊的應用前景。目前，級聯無刷雙饋電機常用的控制方法有矢量控制和無差拍控制，當控制器中使用的電機參數由于溫度、飽和等因素與實際值不同時，控制效果均有不同程度的惡化。為了克服這一問題，該文提出一種基于擴張狀態觀測器的級聯無刷雙饋電機魯棒預測電流控制方法，同時適用于并網同步和發電過程。該方法基于超局部模型使用擴張狀態觀測器來估計系統的動態部分和總擾動，并進一步結合無差拍控制，實現控制繞組電流的快速準確控制。與傳統的矢量控制和無差拍控制進行了比較，實驗結果表明，該方法不僅在電機參數準確時有良好的穩態和動態性能，在電機參數變化時同樣能保持較好的控制效果，具有較強的參數魯棒性。

級聯無刷雙饋電機 擴張狀態觀測器 參數魯棒性 并網同步和發電

0 引言

級聯無刷雙饋電機（Cascaded Brushless Doubly- Fed Generator, CBDFG）由同軸的兩臺繞線轉子異步電機構成，二者的轉子繞組直接相連從而無需電刷和集電環，因此具有使用壽命長、可靠性高、維護成本低等優點[1-2]。CBDFG既可用于獨立發電，也可用于并網發電，在風力發電和水力發電等領域具有廣闊的前景[3]。

目前，國內外學者針對無刷雙饋電機的結構原理、數學模型和等效電路進行了深入研究[4-5]，為高性能閉環控制提供了良好的基礎。在各種閉環控制中，矢量控制（Field-Oriented Control, FOC）較早地在CBDFG控制中得到研究和應用[6]。盡管矢量控制可以獲得良好的穩態和動態性能，但由于它本身的多環系統結構和PI等線性控制器的使用，矢量控制嚴重依賴電機的參數精度并且需要大量的調試整定工作來保證系統的穩定運行[7]。為了消除傳統矢量控制中的控制器整定工作，同時提高動態響應和系統對參數變化的魯棒性，直接轉矩控制和直接功率控制被引入CBDFG控制中[8]。該方法根據電機的功率或轉矩誤差符號以及控制繞組側磁鏈所在扇區，從一個預定的矢量表中選擇能夠減小被控變量誤差的電壓矢量，具有結構簡單、參數魯棒性強、動態性能好等優點。但是由于控制中采用的是一個啟發式矢量表，在某些區域選擇的矢量是無效甚至錯誤的，無法保證功率或轉矩的精確控制，導致被控量脈動較大[9]。

近年來，預測控制以其原理簡單、動態響應快、多目標控制和易于考慮約束等優點在交流電機控制領域得到了廣泛關注[10-12]。預測控制主要包括模型預測控制[13]、無差拍控制[14]等。文獻[13]將完整精確的CBDFG模型用于有限狀態集模型預測控制，考慮了轉子電路的影響，實現了有功和無功的精確解耦控制，由于在每個控制周期施加一個電壓矢量，穩態脈動依然較大并且開關頻率變化。文獻[14]將無差拍預測電流控制（Deadbeat Predictive Current Control, DPCC）用于CBDFG，在固定開關頻率的同時減小了穩態脈動。預測控制用于CBDFG控制的主要問題是效果依賴電機精確模型和電機參數，若電機參數發生變化或者參數辨識不準確，被控量在穩態時會出現明顯的靜差，另外計算量較大。

在實際應用中，如果電機參數發生變化或與控制器中的參數不匹配，傳統控制方法的控制性能將會下降。對于無刷雙饋電機，由于轉子結構封閉，系統各變量之間耦合關系復雜，造成參數辨識困難，控制難度大。因此，魯棒控制受到了廣泛的關注。一般來說，提高控制方法參數魯棒性的主要方法大致可分為三類：在線參數辨識[15]、擾動觀測方法[16-17]和無模型算法[18]。文獻[15]利用一種遞歸最小二乘法在雙饋電機運行期間在線估計電機參數，但此類方法容易增加計算負擔。擾動觀測方法主要是基于擾動觀測器或者擴張狀態觀測器。在文獻[16]中，擾動觀測器被添加到連續時間預測控制方法的控制回路中。當電機參數變化或者外部擾動出現時，電機仍然可以保持良好的控制效果。文獻[17]將基于擴張狀態觀測器（Extended State Observer, ESO）的無模型預測電流控制應用到雙饋電機上，在參數不準確時具有較好的控制性能。文獻[18]將無模型控制方法用于無刷雙饋電機，其主要思想是存儲之前基本電壓矢量作用引起的電流變化代替當前對應電壓矢量的作用效果。但是當一個電壓矢量長時間不作用時，相同電壓矢量作用的效果可能有明顯變化，這會影響系統的穩態性能。

針對CBDFG參數變化的內擾問題，本文使用ESO來估計系統總擾動[19]，提出了一種基于ESO的級聯無刷雙饋電機魯棒預測電流控制（Robust Predictive Current Control, RPCC）。所提方法開關頻率固定，可以實現無差跟蹤，具有良好的參數魯棒性。大部分無刷雙饋電機的控制方法都是針對并網發電過程設計的，雖然現有矢量控制和直接轉矩控制也可以用于并網同步過程[20-21]，但這方面的研究相對較少。本文則把所提出的控制方法用到了并網同步和并網發電全過程。在相同的實驗測試條件下，將其與傳統的FOC和DPCC進行了對比，實驗結果驗證了所提方法的有效性。

1 級聯無刷雙饋電機數學模型

本文以正序連接的級聯無刷雙饋電機為研究對象，其原理結構如圖1所示，包括功率電機和控制電機。以功率電機的定子側為參考，可以得到任意轉速同步旋轉坐標系下的數學模型。當同步坐標旋轉速度等于電網電壓角速度g時，電機的數學模 型為

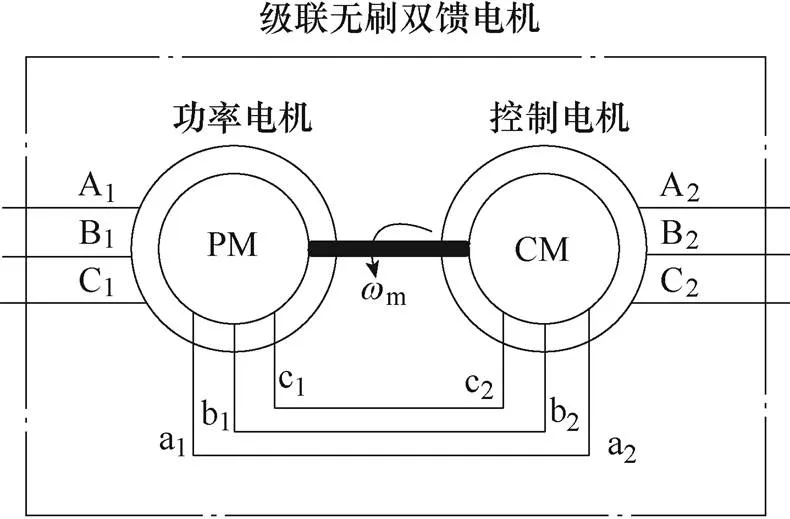
圖1 正序連接的級聯無刷雙饋電機結構

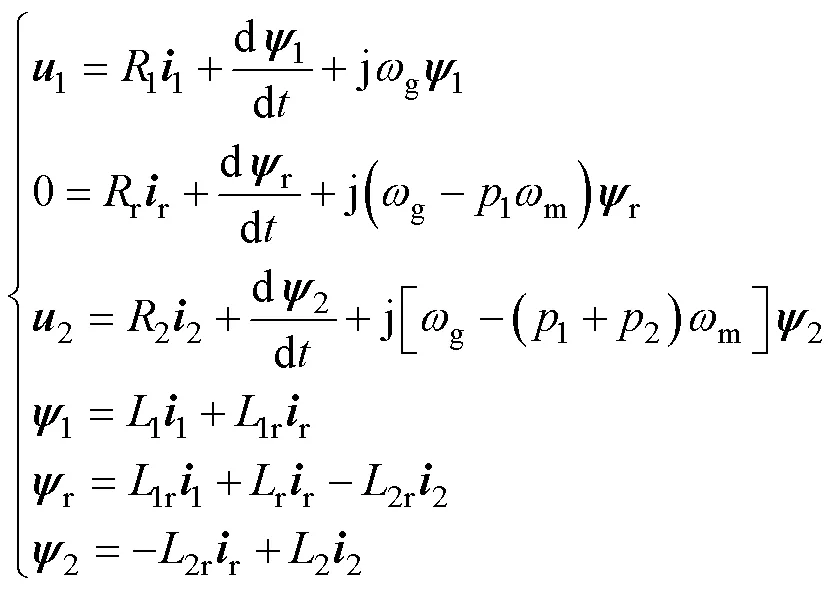
式中，、和分別為電壓、電流和磁鏈矢量；、和分別為繞組電感、繞組電阻和極對數；下標1、2和r分別為功率繞組、控制繞組和轉子參數；m為轉子機械角速度。

本文以電網電壓作為d軸進行定向，功率電機側的輸出有功功率、無功功率可以分別表示為

2 并網同步控制

同步過程中，顯然功率側不發出功率，功率側電流1=0，繼而通過式（1）可得

根據式（4），設計磁鏈外環PI為

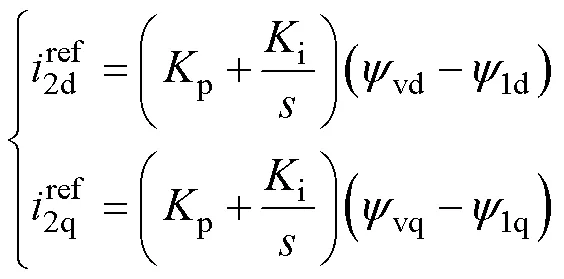
式中，下標“d”和“q”代表對應變量的d軸分量和q軸分量；p和i分別為PI中的比例增益和積分增益。

3 并網發電控制

3.1 控制繞組電流參考值計算

發電過程中，由式（1）可得

求解式（6），可以得到功率電流1和控制電流2之間的動態關系為

由式（2）和式（7）設計功率外環PI為

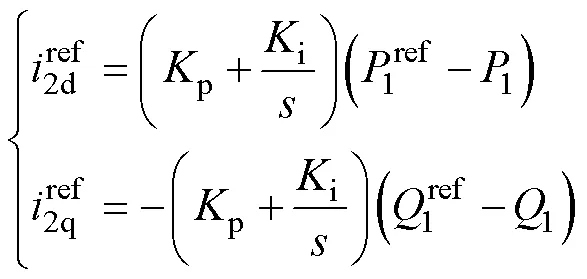
式中，上標“ref”為對應變量的參考值。

3.2 基于ESO的電流估計和預測

由式（1）可以得到控制電流與3個磁鏈之間的關系為

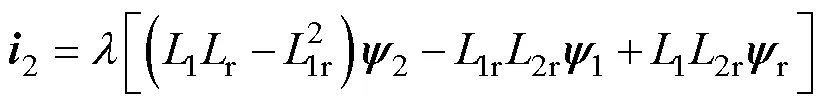
其中

將式（1）與式（9）相結合，可以得到控制電流對時間的微分為

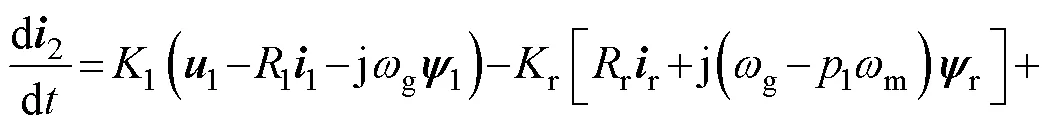
其中

ESO可以將總擾動（包括不確定的系統變量和外部擾動）擴展為一個新擾動，并將這個總擾動反饋給被控制系統，使系統的控制方法既能觀察到模型的非線性部分，又能觀察到未知的外部擾動。為提高控制方法參數魯棒性，將式（10）寫為超局部模型，有

式中，為系統的總擾動。在中捕捉參數不匹配或參數變化引起的擾動，并由ESO實時觀察，以便在控制算法中進行補償。使用式（11）模型，不需要使用式（1）中CBDFG的完整模型來構建ESO。

在此基礎上，采用線性ESO將傳統的非線性誤差函數替換為線性誤差函數[19]。雖然線性ESO的性能可能不如非線性ESO，但設計簡單。

根據式（11），系統是一階單輸入單輸出系統。因此，在離散域，ESO的狀態空間方程可以表示為

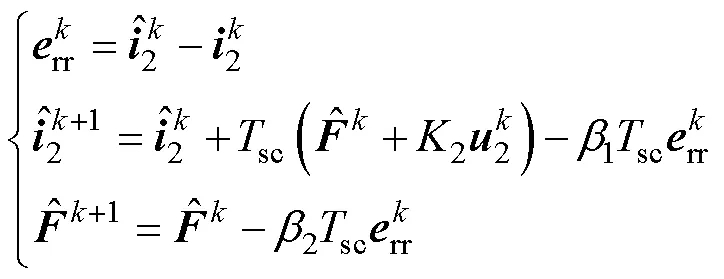
根據式（12），通過將采樣的控制電流作為輸入，估計的控制電流作為輸出，控制電壓為擾動項，可以得到域下的ESO結構框圖，如圖2所示。無刷雙饋電機的擴張狀態觀測器閉環傳遞函數為

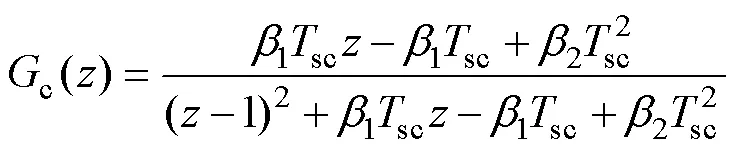
則系統的閉環特征方程為

當離散系統所有的特征根分布在域上的單位圓時，系統是穩定的。經過參數整定后，特征方程的極點可以放在同一個點上。因此，擴張狀態觀測器的參數可以表示為

圖2 離散域下擴張狀態觀測器的結構框圖

由此可見，是擴張狀態觀測器的唯一需要整定的參數。接下來，結合所提RPCC對進行設計。

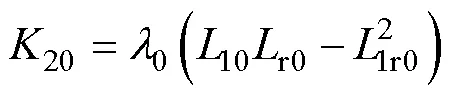
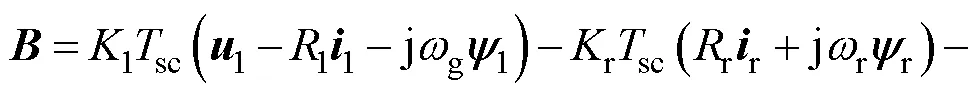
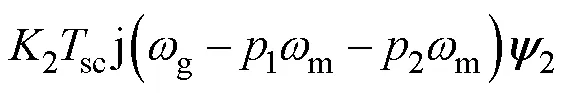
根據圖3，實際控制電流值與參考值之間的關系為

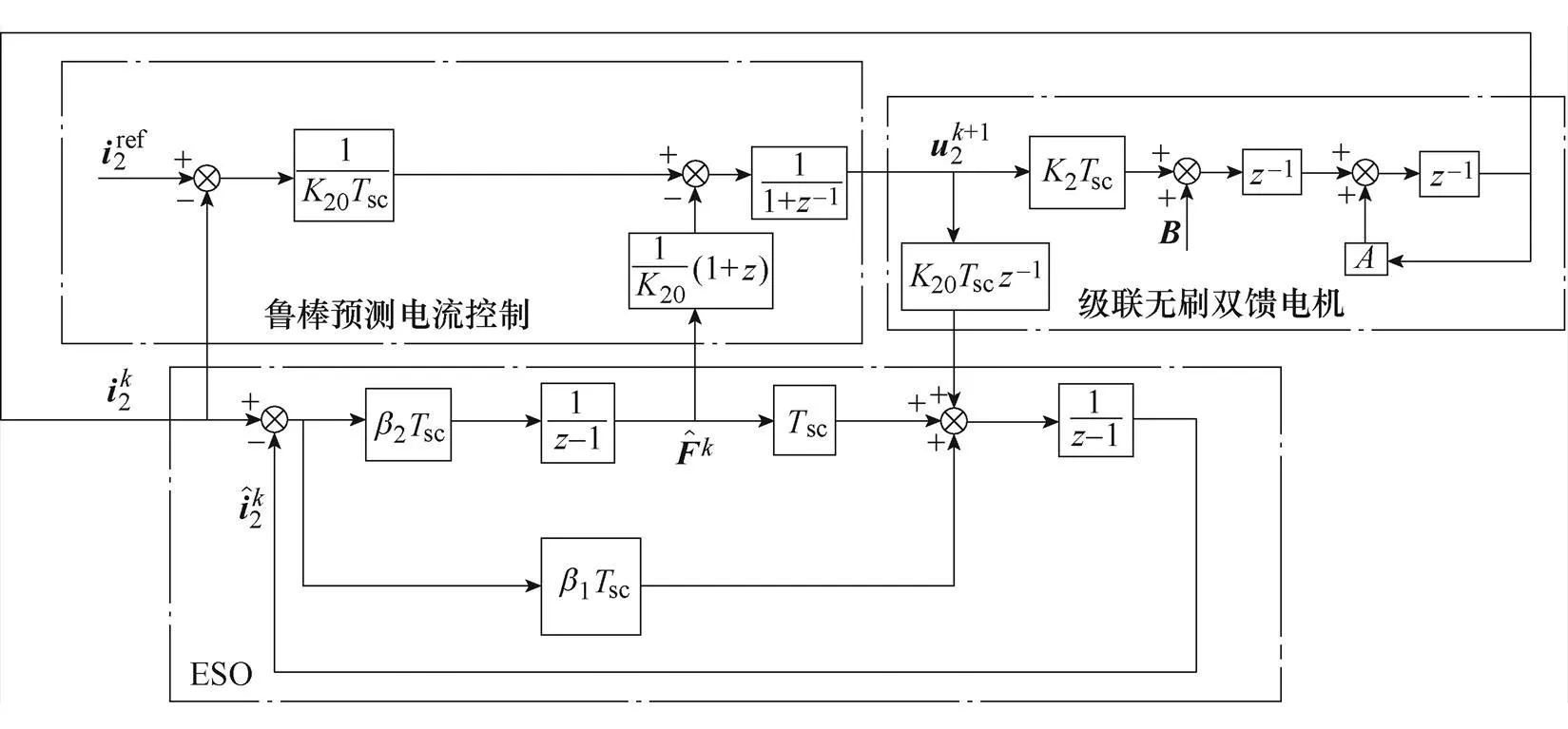
圖3 RPCC的結構框圖

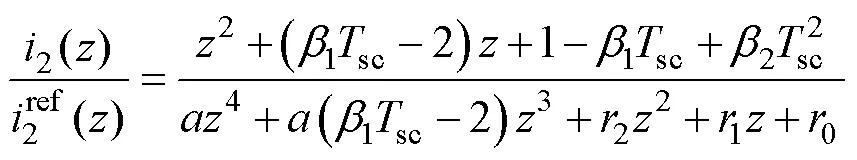
其中

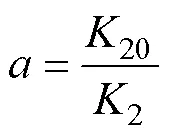
所提RPCC的特征方程為

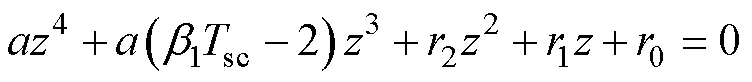
為了設計合適的ESO參數，假設沒有電感誤差，即=1。RPCC的特征方程可以簡化為

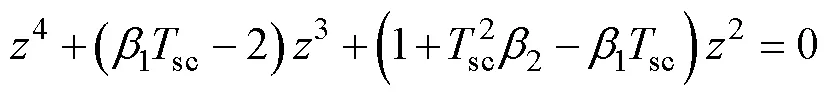
考慮式（15），特征方程的根為1,2=0，3,4=。

上述對參數的設計是在忽略電感誤差的基礎上得到的，接下來對系統能夠穩定運行的參數不匹配范圍進行分析。通過將式（18）的特征方程轉化到域中，并使用羅斯判據，可得取0.52，采樣頻率sc=10 kHz時參數不匹配的穩定范圍為＞0.563 4，即

3.3 魯棒預測電流控制

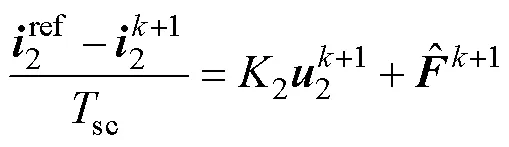
因此，聯立式（21）和式（22），可以得到在同步dq坐標系下的控制電壓參考值為

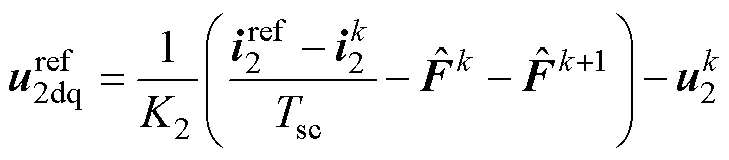
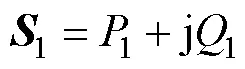
圖4 基于ESO的級聯無刷雙饋電機魯棒預測電流控制方法結構框圖

Fig.4 Structure block diagram of robust predictive current control method for cascaded brushless doubly-fed generator based on ESO

4 仿真和實驗驗證

本文為了證明所提方法的有效性，在CBDFG實驗平臺上進行了測試，實驗平臺如圖5所示。實驗所使用的控制電機和功率電機的參數見表1。所有的實驗結果都是通過與MicroLabBox和PC接口的ControlDesk進行記錄，然后利用Matlab軟件對存儲的數據進行分析和繪制。實驗所使用的電網相電壓有效值和母線電壓分別為75 V和150 V，采樣頻率為10 kHz。

4.1 并網同步過程

圖6為所提方法從同步過程切換到發電過程的實驗結果。四個通道從上到下分別為功率繞組三相電流、功率繞組磁鏈、功率繞組感應線電壓和控制繞組三相電流。圖6中，實線表示采樣的實際值，虛線表示對應變量的參考值。可以看出，功率側的磁鏈和感應電壓基本與參考值重合。在0.08 s左右功率繞組接入電網，切換后功率側電流無明顯沖擊，系統可以在不同過程之間平滑切換。

圖5 級聯無刷雙饋電機實驗平臺

表1 級聯無刷雙饋電機參數

4.2 并網發電過程

圖7為所提方法在轉速350 r/min下的穩態實驗結果。有功功率參考值為-350 W，無功功率參考值為0 var。圖7a從上到下依次為：功率繞組有功功率、功率繞組無功功率、功率繞組三相電流、控制繞組三相電流。由圖7b可知，功率繞組a相電流總諧波畸變率（Total Harmonic Distortion, THD）為1.116 9%，該方法在穩態下具有良好的控制性能。

圖6 所提控制方法從同步過程切換到發電過程的實驗波形

圖7 所提控制方法在轉速350 r/min下的穩態實驗結果

Fig.7 Steady-state experimental results of the proposed control method at 350 r/min

圖8為所提控制方法在功率階躍變化下的實驗動態波形。0.06 s時，有功功率參考值從0 W變為-350 W。有功功率較快跟蹤參考值，由于所提方法外環PI做了相應的簡化，階躍條件下無功功率和有功功率的控制存在一定的耦合，但是無功功率的波動范圍較小并且能迅速穩定。

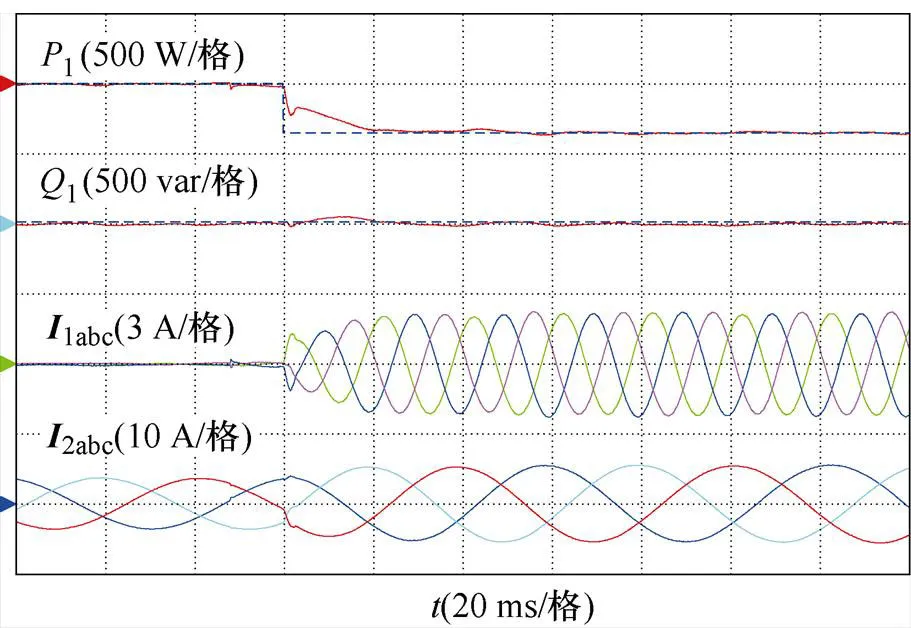
圖8 所提控制方法在有功功率階躍下的實驗波形

FOC、DPCC和本文所提出的RPCC-ESO方法的實驗數據對比見表2。相比于前兩種傳統的控制方法，所提控制方法在不同轉速下穩態功率繞組電流THD都更小。

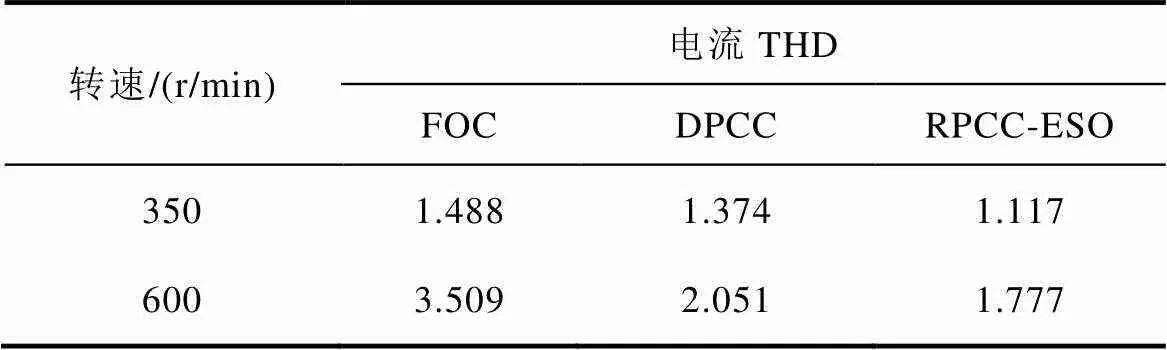
表2 三種控制方法在不同轉速下a相穩態功率電流的THD對比

圖9為所提控制方法在轉速由亞同步速變到超同步速的動態波形。轉子轉速從450 r/min增加到550 r/min，有功功率參考值為-350 W。當轉速接近同步轉速時，控制繞組電流變為直流，但功率跟蹤和功率繞組電流不受影響。

實際風電系統考慮到開關損耗，開關頻率往往定在幾千赫茲。為了展示本文所提RPCC-ESO方法在低開關頻率下的效果，通過仿真，將采樣頻率為3、5和7 kHz的電流THD與10 kHz的電流THD對比。仿真使用參數與實驗完全相同，轉速為350 r/min，有功功率參考值為-350 W，無功功率參考值為0 var，對比結果見表3。可以看出，雖然開關頻率的下降會使電流THD有所升高，但仍然遠小于5%，滿足并網要求。

圖9 所提控制方法在轉速變化下的實驗波形

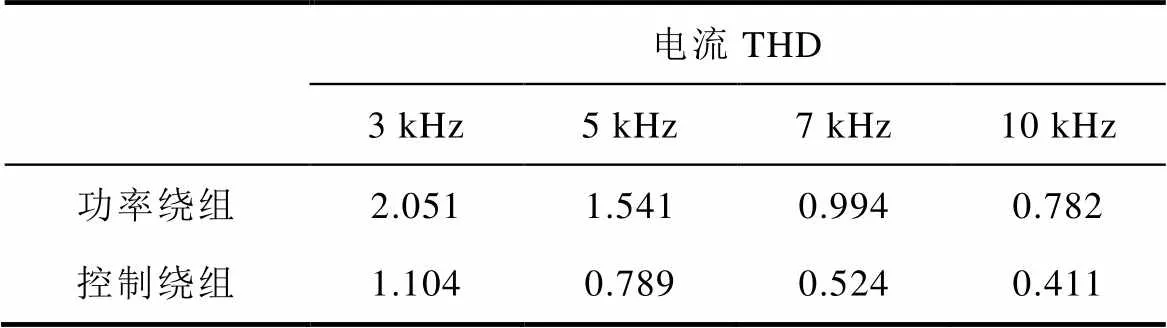
表3 所提控制方法在不同采樣頻率下a相穩態功率電流和控制電流的THD對比

4.3 參數魯棒性實驗

圖10給出了三種控制方法在功率繞組互感參數1r變化下的實驗結果。在實驗中人為改變控制器中的電感參數，功率參考值和電機轉速維持不變。圖10分別給出了矢量控制、無差拍控制和所提控制方法的實驗結果。

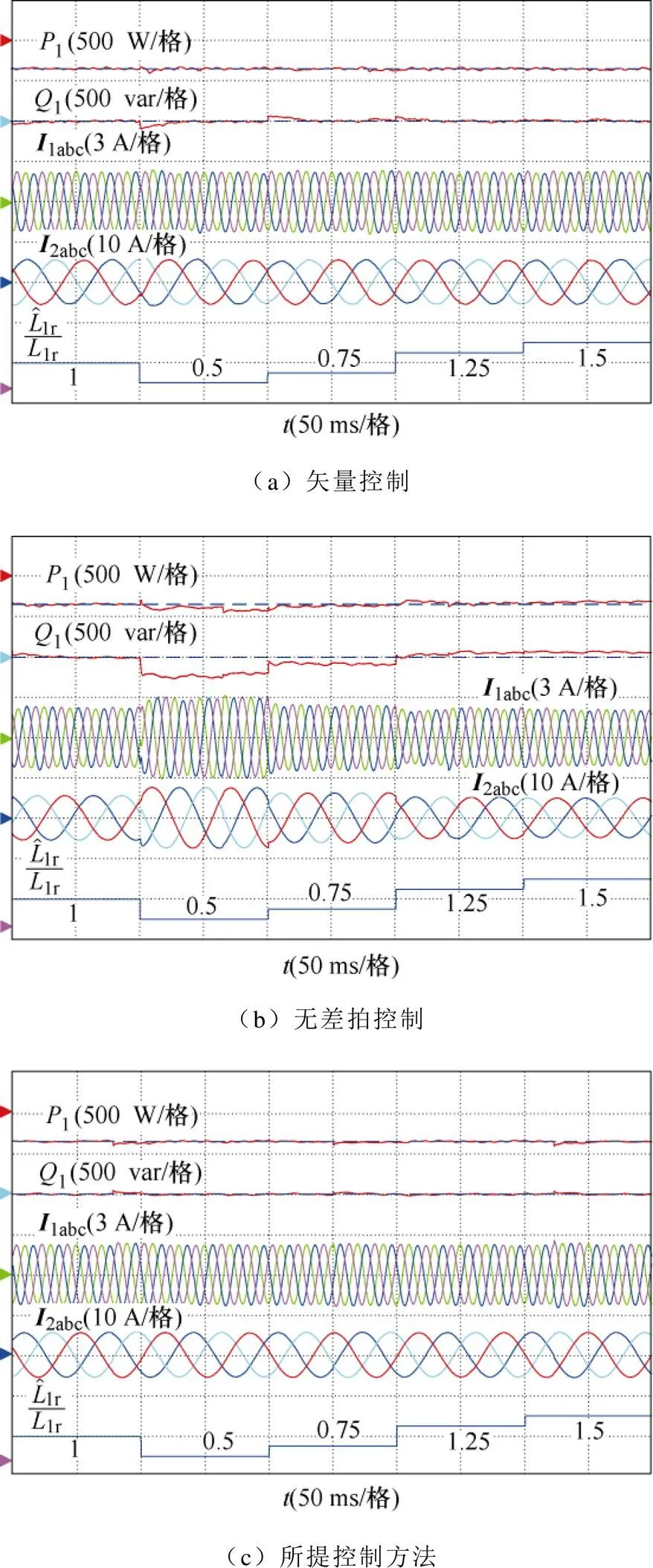
圖10 三種控制方法在功率繞組互感L1r變化的實驗結果

可以看出，矢量控制的功率跟蹤略有波動，效果雖然不如所提控制方法，但明顯好于無差拍控制方法。這是由于矢量控制的補償項和PI參數的整定雖然與電機參數有關，但改變控制器中的電機參數后，外環PI可以消除功率靜差。無差拍控制的功率跟蹤會出現靜差，相應的功率繞組電流也會發生變化。這是由于無差拍控制本身的公式推導用了完整的電機數學模型，更容易受到參數不匹配的影響。

對于所提方法，不管互感參數如何變化，控制效果基本與參數準確的穩態實驗結果一致，具有良好的參數魯棒性。這是由于該方法的ESO內環不使用電機參數進行控制。

值的一提的是，雖然FOC和所提方法最后均能實現無差跟蹤，但是FOC的內環PI參數一般根據截止頻率來進行設計，其與控制器中的電機參數有關。因此，當控制器中的電機參數與實際值不匹配時，電流環的控制效果會受到影響，而所提方法的內環參數設計與電機參數無關，具有更強的魯棒性。

由于功率繞組互感參數1r對功率跟蹤影響較大，受限于篇幅，本文只給出了1r變化下的實驗結果。對于控制繞組互感參數2r，三種控制方法造成的功率波動范圍與1r接近。對于轉子電阻參數r，矢量控制基本不受影響，所提控制方法由于不使用電阻參數，故不受影響，無差拍控制的功率跟蹤會出現靜差。控制繞組電阻參數2對三種控制方法的影響均可忽略。

5 結論

本文提出了一種基于ESO的級聯無刷雙饋電機魯棒預測電流控制方法。實驗結果證明了基于ESO的控制方法不僅在電機參數準確時有較好的穩態和動態波形，在電機參數變化時同樣能保持較好的控制效果。相比于傳統方法，本文方法具有以下優點：

1）既可以用于并網同步過程，也可以用于并網發電過程。

2）使用線性ESO，經過參數整定后，需要設計的控制器參數只有一個，相比于傳統矢量控制顯著減少了調試時間。

3）基于超局部模型使用ESO快速估計模型不確定性引起的總擾動，并進一步結合無差拍控制，實現控制繞組電流的快速準確控制。相比傳統的矢量控制和無差拍預測控制，該方法有更好的參數魯棒性。

[1] Liang Shuai, Jin Shi, Shi Long. Research on control strategy of grid-connected brushless doubly-fed wind power system based on virtual synchronous generator control[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(4): 404-412.

[2] 闞超豪, 鮑習昌, 王雪帆, 等. 無刷雙饋電機的研究現狀與最新進展[J]. 中國電機工程學報, 2018, 38(13): 3939-3959, 4036.

Kan Chaohao, Bao Xichang, Wang Xuefan, et al. Overview and recent developments of brushless doubly-fed machines[J]. Proceedings of the CSEE, 2018, 38(13): 3939-3959, 4036.

[3] 程明, 許利通, 曹政, 等. 級聯式無刷雙饋電機的矢量控制系統和功率流研究[J]. 電工技術學報, 2022, 37(20): 5164-5174.

Cheng Ming, Xu Litong, Cao Zheng, et al. Study on vector control system and power flow of cascaded brushless doubly-fed induction generator[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(20): 5164-5174.

[4] 任泰安, 梁克靖, 王群京, 等. 差調制無刷雙饋電機轉子繞組設計及性能分析[J]. 電機與控制學報, 2022, 26(4): 57-65.

Ren Taian, Liang Kejing, Wang Qunjing, et al. Rotor winding design and performance analysis of differ- ential modulation brushless doubly-fed machines[J]. Electric Machines and Control, 2022, 26(4): 57-65.

[5] 程明, 韓鵬, 魏新遲. 無刷雙饋風力發電機的設計、分析與控制[J]. 電工技術學報, 2016, 31(19): 37- 53.

Cheng Ming, Han Peng, Wei Xinchi. Design, analysis and control of brushless doubly-fed generators for wind power application[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 37-53.

[6] Cheng Ming, Luo Rensong, Wei Xinchi. Design and analysis of current control methods for brushless doubly fed induction machines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 717-727.

[7] Esfandiari G, Ebrahimi M, Tabesh A. Instantaneous torque control method with rated torque-sharing ratio for cascaded DFIMs[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8671-8680.

[8] Sadeghi R, Madani S M, Ataei M, et al. Super- twisting sliding mode direct power control of a brushless doubly fed induction generator[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 9147-9156.

[9] Sadeghi R, Madani S M, Ataei M. A new smooth synchronization of brushless doubly-fed induction generator by applying a proposed machine model[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 371-380.

[10] 魏新遲, 許利通, 駱仁松, 等. 考慮飽和效應的無刷雙饋發電機功率模型預測控制[J]. 電工技術學報, 2021, 36(17): 3721-3729.

Wei Xinchi, Xu Litong, Luo Rensong, et al. Model predictive power control of brushless doubly-fed induction generator considering saturation effect[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3721-3729.

[11] 卜飛飛, 羅捷, 劉皓喆, 等. 雙繞組感應發電機系統無差拍電流預測控制策略[J]. 電工技術學報, 2021, 36(24): 5213-5224.

Bu Feifei, Luo Jie, Liu Haozhe, et al. Deadbeat predictive current control strategy of dual winding induction generator system[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5213-5224.

[12] 章回炫, 范濤, 邊元均, 等. 永磁同步電機高性能電流預測控制[J]. 電工技術學報, 2022, 37(17): 4335-4345.

Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.

[13] Wei Xinchi, Cheng Ming, Zhu Jianguo, et al. Finite- set model predictive power control of brushless doubly fed twin stator induction generator[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2300-2311.

[14] Li Xuan, Peng Tao, Dan Hanbing, et al. A modulated model predictive control scheme for the brushless doubly fed induction machine[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 1681-1691.

[15] Bhattarai R, Gurung N, Ghosh S, et al. Parametrically robust dynamic speed estimation based control for doubly fed induction generator[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6529-6542.

[16] Errouissi R, Al-Durra A, Muyeen S M, et al. Offset- free direct power control of DFIG under continuous- time model predictive control[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2265-2277.

[17] Zhang Yongchang, Jiang Tao, Jiao Jian. Model-free predictive current control of DFIG based on an extended state observer under unbalanced and dis- torted grid[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(8): 8130-8139.

[18] 徐偉, 陳俊杰, 劉毅, 等. 無刷雙饋獨立發電系統的改進無參數預測電流控制[J]. 電工技術學報, 2021, 36(19): 4002-4015.

Xu Wei, Chen Junjie, Liu Yi, et al. Improved non- parametric predictive current control for standalone brushless doubly-fed induction generators[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(19): 4002-4015.

[19] Liu Feng, Liu Zhangwei, Mei Shengwei, et al. ESO- based inertia emulation and rotor speed recovery control for DFIGs[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1209-1219.

[20] Broekhof A, McMahon R, Tatlow M. Vector- controlled grid synchronization for the brushless doubly-fed induction generator[C]//7th IET Inter- national Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 2014: 1-5.

[21] Sadeghi R, Madani S M, Agha Kashkooli M R. Grid synchronization of brushless doubly fed induction generator using direct torque control[C]//2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 2016: 53-57.

Robust Predictive Current Control for Grid Synchronization and Power Generation of Cascaded Brushless Doubly-Fed Generators Based on Extended State Observer

（School of Electrical and Electronic Engineering North China Electric Power University Beijing 102206 China）

The cascaded brushless doubly-fed generator (CBDFG) comprises two coaxial wound rotor induction motors, and its rotor windings are directly connected to eliminate the need for brushes and slip rings. Therefore, it has the advantages of long service life, high reliability, and low maintenance cost. CBDFG can be used for independent generation and grid-connected generation, which has broad prospects in wind power and hydroelectric power generation. At present, vector control and deadbeat control are commonly used to control the CBDFG. Because the above two methods use a large number of motor parameters, when the machine parameters in controllers are different from the actual values due to temperature, saturation, and other reasons, the control effects have varying degrees of deterioration. Therefore, this paper proposes an extended state observer (ESO) based robust predictive current control (RPCC) method for CBDFG.

Firstly, the proposed RPCC can be applied to grid synchronization and power generation processes. The only difference between the two processes is the reference value calculation of the control winding current. In the process of grid synchronization, because the power side does not emit power, the virtual flux is needed to calculate the reference value of the control winding current. During the power generation process, the reference value of the control winding current is calculated directly according to the power reference value.

Secondly, the proposed RPCC is based on an ultra-local model and uses an ESO to rapidly estimate the total disturbance caused by model uncertainty. The ESO can extend the total disturbance to a new disturbance and feed this total disturbance back to the controlled system. Based on the state space equation of ESO, the closed-loop transfer function of the ESO for CBDFG is obtained, and the two parameters of ESO are simplified to one. Then, the control block diagram of the proposed RPCC in thedomain is given, and the parameters of ESO are designed according to the characteristic equation of the proposed RPCC. In addition, the parameter stability of the proposed ESO is analyzed.

Finally, according to the designed ESO parameters and the obtained disturbance values, one-step delay compensation is carried out for the current value of the control winding, and deadbeat control is further incorporated to achieve fast and accurate control of the control winding current.

Compared with the traditional field-oriented control and deadbeat control, the experimental results show that this method has good steady-state and dynamic waveforms when the motor parameters are accurate and maintains a good control effect when the CBDFG parameters change. This method has good parameter robustness. The switching frequency is usually set at several kHz to reduce the switching loss in an actual wind power system. The simulation results of the proposed RPCC at low switching frequencies show that although the decrease in switching frequency increases the current THD, it is still far less than 5%, which meets the grid-connection requirements.

Cascaded brushless doubly-fed generator, extended state observer, parameter robustness, grid synchronization and power generation

楊長山 男，2000年生，碩士研究生，研究方向為無刷雙饋電機模型預測控制。E-mail: yangchangshanyx@163.com

張永昌 男，1982年生，教授，博士生導師，研究方向為電力電子與電機控制等。E-mail: zyc@ncepu.edu.cn（通信作者）

TM346

10.19595/j.cnki.1000-6753.tces.L10095

國家自然科學基金（52077002）、國家重點研發計劃（2021YFB2400702）和華能集團總部科技項目海上風電與智慧能源系統科技專項（一期）（HNKJ20-H88）資助項目。

2023-01-03

2023-02-21

（編輯 崔文靜）