基于EEMD的固定分段數分段線性表示方法
劉學彬,梁智飛,朱衛平,祝 凱*
(1.青島理工大學 信息與控制工程學院,山東 青島 266000;2.中石油煤層氣有限責任公司,北京 102200)
0 引 言
由于時間序列是高維且存在大量噪音的,直接在原始序列上進行預測、模式發現和分類等挖掘任務的效率較低,同時也會影響挖掘結果的精度和可信度。因此,使用特征表示方法將時間序列從高維度轉換到低維度,這種方法可以在降低時間序列復雜度的同時,保留時間序列的主要信息,為進一步深入研究時間序列奠定基礎[1]。
目前國內外有不少學者致力于時間序列特征表示方法的研究,時間序列特征表示方法的主要代表有:基于域變換的表示方法(離散傅里葉變換[2]和離散小波變換[3];符號化表示方法,其中應用最廣泛的是符號聚合近似方法[4-5];分段累計近似方法[6]和分段線性表示(Piecewise Linear Representation,PLR)[7]。其中PLR具有簡單、直觀的特點,能夠有效保留原序列的形態信息以減少擬合誤差,是一種應用廣泛的時間序列特征表示方法。因此,該文著眼于分段線性表示方法的研究和改進。
目前,PLR的研究主要集中于解決分段數和分段點的選擇問題上。為了解決這些問題,時序的分段表示方法可以分為以下幾種:(1)限制分段數:主要代表是分段累計近似方法,但該方法沒有考慮實際序列形態,不能很好地保留原始序列特征;(2)限制分段誤差:主要代表性算法有自頂向下[8]、自底向上[9]、滑動窗口[10]。限制分段誤差方法對一些狀態變化的拐點不敏感,不能保證每一分段只具有一種基本趨勢。針對上述問題,近年來不少學者提出了一些改進方法。例如,尚福華[11]和廖俊[12]提出基于趨勢轉折點的分段線性表示方法;陳帥飛[13]提出基于關鍵點的分段線性表示方法;劉意楊[14]提出基于轉折點和趨勢段的分段線性表示方法等。但是,這些方法使用單一的啟發式規則,難以適用于數據分布復雜的時間序列,進而導致算法出現局部最優化問題,而且不能靈活控制壓縮率,不能適應后期要求分段數一定的應用[15]。
針對上述方法存在局部最優化和不能預計分段數的問題,提出了基于EEMD的固定分段數分段線性表示方法。首先,通過模態重構思想過濾掉細節信息,提取到全局性分段點;然后,根據各初始分段子序列的波動程度,確定子序列段內分段點數量分布;最后,采用基于分段數閾值的自底向上方法將子序列合并到要求的分段數。
1 分段線性表示相關概念及問題描述
1.1 分段線性表示相關概念
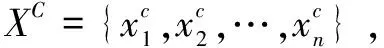
(1)
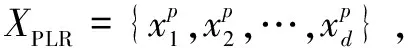
(2)
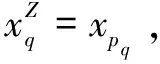
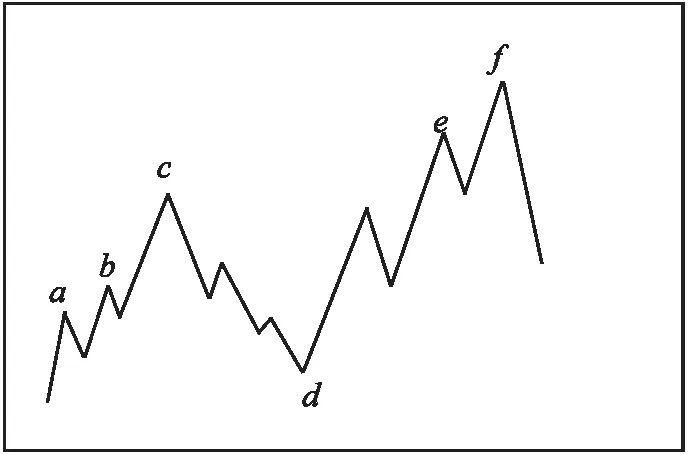
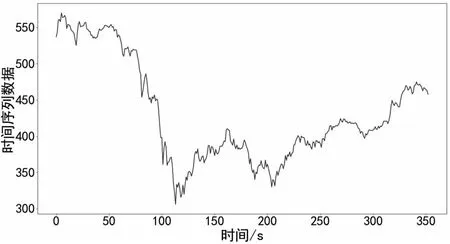
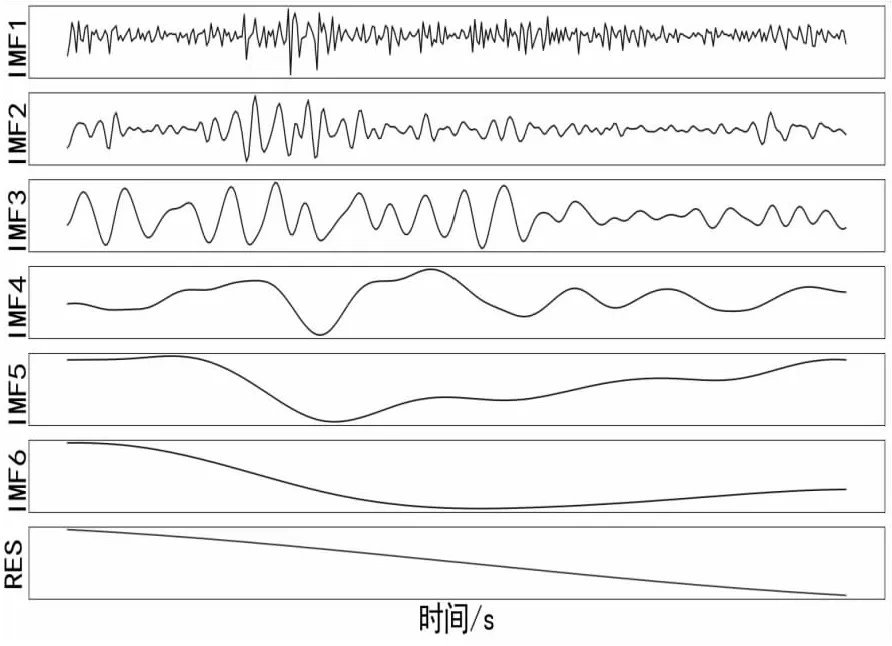
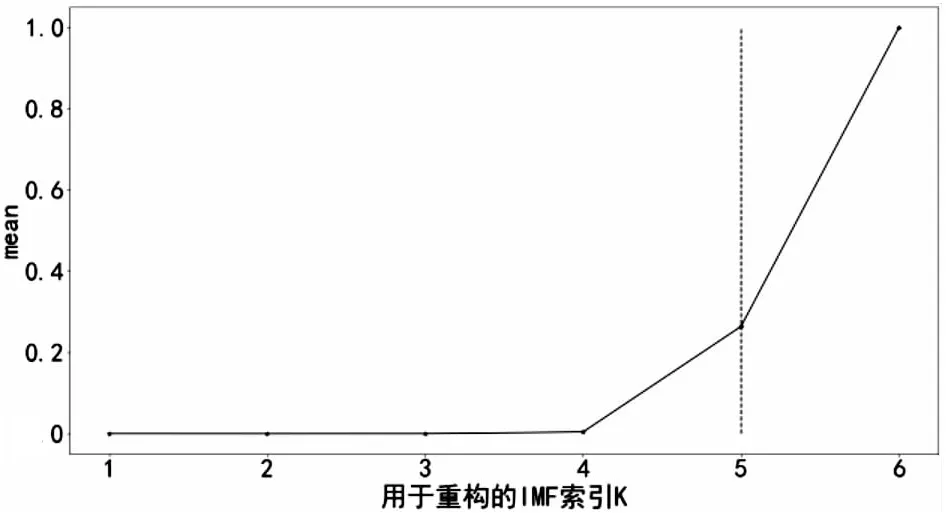
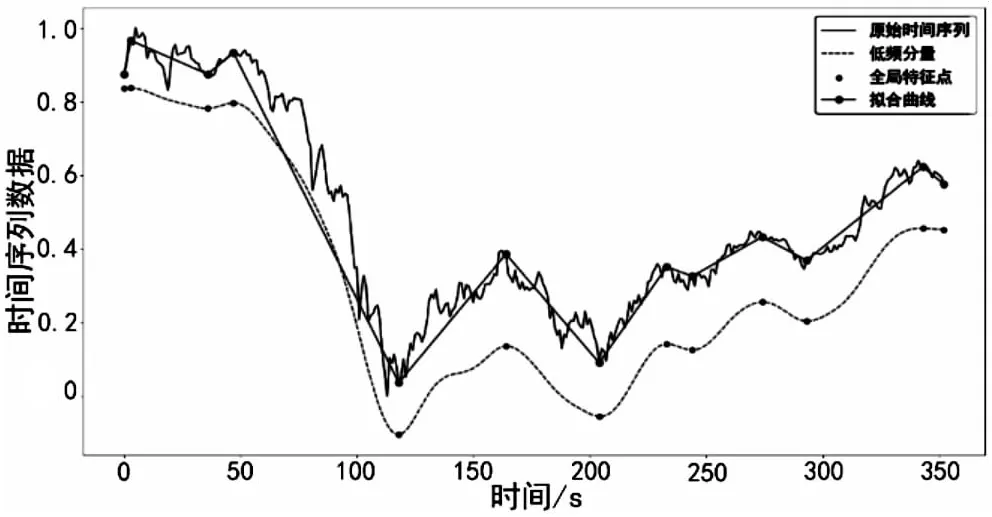
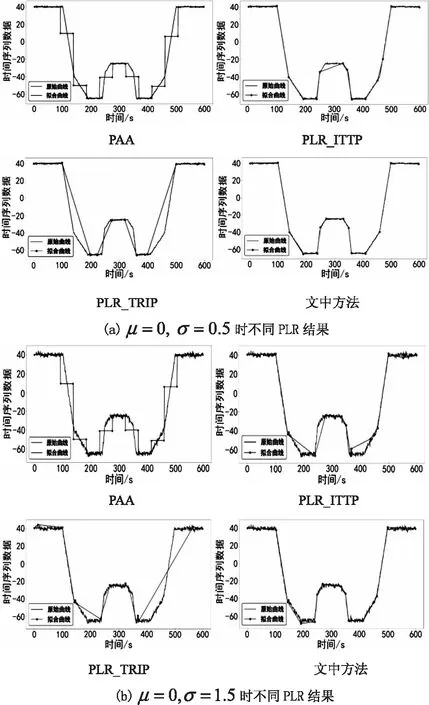
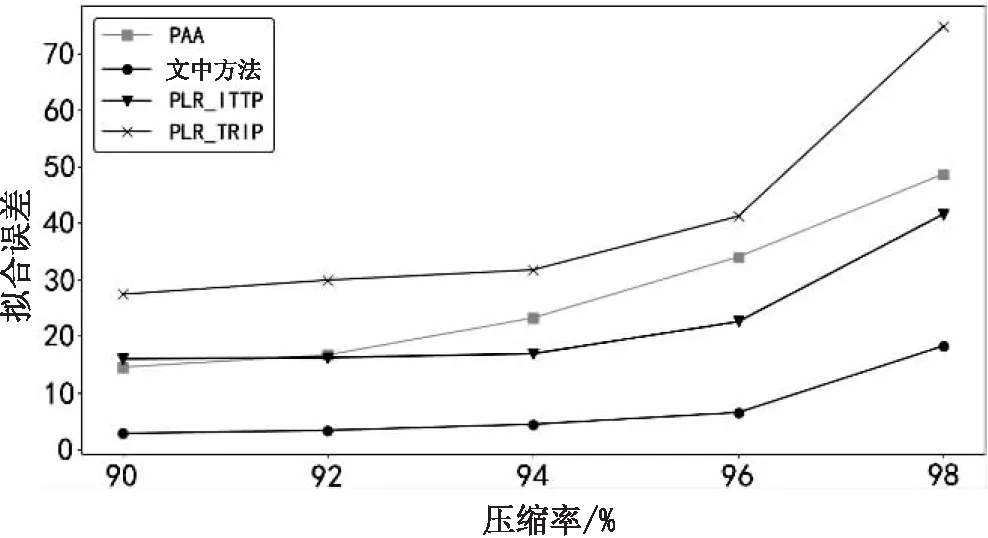
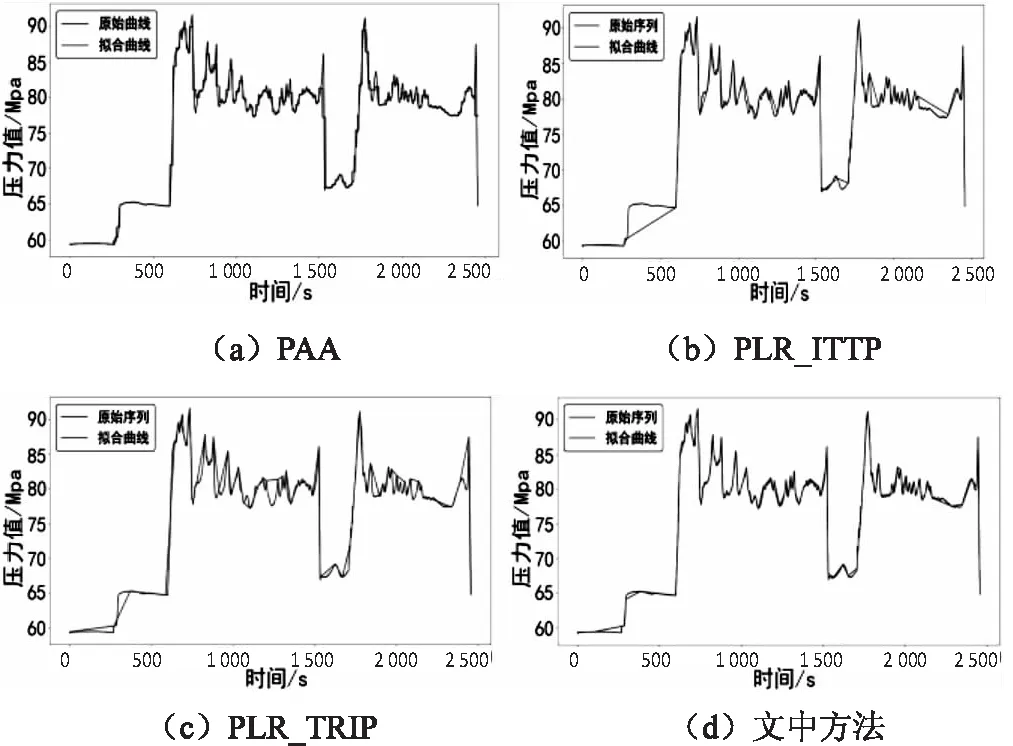
{xpq-1≤xpq}∩{xpq+1 或 {xpq-1≥xpq}∩{xpq+1>xpq}∪{xpq-1>xpq}∩{xpq+1≥xpq} (3) 此外,規定一個有限長度的時間序列起點和終點為重要點。由式(3)得到m個重要點,則重要點序列表示為: (4) 傳統的算法采用單一的啟發式規則提取局部特征點,當原始時間序列波動頻率較為劇烈且集中時,容易出現多個點的斜率變化近似。時間序列如圖1所示。 圖1 斜率波動頻繁劇烈的情況 圖1中序列點a,b,c,d,e,f點斜率變化近似,當通過調節斜率變化閾值d使得達到要求的壓縮率時,會出現臨界閾值,如下: 其中,下標L表示左,R表示右。由上述公式和圖1知,c,d兩點作為反映序列整體趨勢的特征點因斜率變化小而“漏提取”,即分段方法的結果遺漏掉能夠反映整體特征的數據點;由此可認為,b,e兩點為“過提取”,即分段方法的結果提取到不能反映整體特征的數據點,導致算法陷入局部最優化。 Huang[17]提出了經驗模態分解(Empirical Mode Decomposition,EMD)。該方法的核心思想是將復雜的信號分解為有限個頻率從高到低的本征模態函數(Intrinsic Mode Functions,IMF),對于某時間序列{x(t)}經驗模態分解的具體步驟如下: (1)求出{x(t)}中所有的極值。 (2)采用3次樣條函數進行插值擬合上包絡線bmax(t)和下包絡線bmin(t)。 (3)計算上下包絡線平均值m(t): m(t)=[bmax(t)+bmin(t)] (5) (4)從時間序列中提取均值并將x(t)和m(t)的差定義為: d(t)=x(t)-m(t) (6) (5)檢查d(t)的屬性:如果滿足IMF分量條件,則將d(t)表示為第k個IMF,并將x(t)替換為殘差r1(t)=x(t)-d(t)。第k個IMF分量通常表示為ck(t);如果不滿足,則將x(t)替換為d(t)。 (6)重復步驟(1)~(5)直到殘差為單調函數為止。 原始時間序列可以表示為若干個IMF和一個殘差的線性組合: (7) 其中,x(t)表示1維信號;ck(t)表示第k個IMF分量;r(t)表示殘余。 當時間序列的時間尺度呈現跳躍性時,采用EMD對其進行分解,將會產生一個IMF分量包含不同時間尺度特征成分的情況,這種現象被稱為模態混疊[18],它使得EMD得到的分解結果的可靠性和可解性受到影響。Wu[18]提出了集合經驗模態分解(Ensemble Empirical Mode Decomposition,EEMD)解決這一問題。基本思想是將不同白噪聲多次加入原始時間序列以消除模態混疊現象。 如圖2(a)所示,對1組示例時間序列進行EEMD分解,得到了6個IMF分量和1個RES殘余,如圖2(b)所示。 Zhang等人[19]采用EEMD技術來分析石油價格 (a)示例時間序列 (b)EEMD分解結果圖2 示例時間序列集合經驗模態分解 變化。他們發現,經本征模態函數重構后的序列可以很好地反映序列的關鍵轉折點和整體趨勢變化。基于這項研究,該文使用EEMD技術對時間序列進行分解,并將分解得到的IMF分為高頻部分、低頻部分和殘余。前兩個成分能夠揭示時間序列所蘊含的物理意義,并發現時序的一些新特征。對EEMD分解得到的N個IMF,求出每個IMF的平均值,得到用于分解高頻和低頻分量的K函數。以圖2(a)的時間序列為例,構建的K函數及高、低頻和殘余分量如圖3所示。 (a)分解高頻和低頻分量的K函數 (b)原始時序和3個分量圖3 K函數及對應的3個分量 由圖3(a)知,在IMF5處,平均值開始偏離零點,因此使用IMF1~IMF4的部分重構表示高頻分量,使用IMF5和IMF6的部分重構表示低頻分量,殘余單獨處理。圖3(b)顯示了原始時間序列和3個分量。殘余反映時間序列長期緩慢變化;低頻分量的每次急劇上升或下降可能對應1個物理事件或是某種程度上的噪聲表征;而高頻分量通過去除大量的小幅波動使得可以反映時間序列的整體變化趨勢。下面給出模態重構序列的定義。 定義4(模態重構序列):對于某時間序列X,對X進行EEMD分解得到N個IMF,定義參與重構的起始IMF索引為s,終止索引為e,重構序列XR表示為: (8) 在高頻分量基礎上,提取全局特征點,實現時間序列的初始分段。 (9) 根據上式,對圖3(b)中的高頻分量提取全局特征點,實現時間序列的初始分段。 由圖4知,原始時間序列被全局特征點分割為12段子序列,每段子序列都保持整體上升、下降、保持三種基本趨勢,有效去除大量小幅波動,反映時間序列整體變化趨勢。 圖4 全局特征點初始分段 假設在序列中需要查找N個分段點,上節已提取了M個全局特征點,并將原時間序列分成了M+1個初始段。接下來,采用廖俊[12]提到的時間序列點間的模式變化提取剩下的N-M個分段點,如圖5所示。 為了反映時間序列內的模式變化,將所有時間序列數據點符號化[20]。在時間序列X中,給定某一序列點xj,然后分別用前一點xi和后一點xk與該點做差分,即xk-xj=Q和xj-xi=P。具體步驟如下[1]: (3)將不符合上述條件的點用“0”表示。 (4)遍歷整個序列,得到符號化序列。 圖5 時間序列3點之間的模式變化 其中δ為自定義閾值,將所有符號化的子序列分別求和,存入Hi中,得到長度為M+1的序列:H={H1,H2,…,HM+1},通過以下公式: (10) 得到M+1個子序列內分段點的分布數量: C={C1,C2,…,CM+1} (11) 經典的自底向上方法由Keogh等人[7]提出,該方法的基本思想是通過循環地合并誤差最小的相鄰分段,直到所有的擬合誤差均不小于分段閾值為止。該算法存在偶數限制的不足,為了解決該問題,孫煥良在其[21]研究中提出了優化的PLR_BU算法,但是仍無法準確地預測時間序列的分段數。 針對這一缺陷,該文在優化的PLR_BU算法基礎上進行了改進,提出了固定的PLR_BU算法。該算法的基本思想:首先將長度為n的時間序列依次相連前后兩點,然后給定分段數閾值,循環地執行下述過程:(1)計算相鄰的分段合并后的擬合誤差;(2)查找擬合誤差最小的相鄰分段{xi,xj,xk},移除此相鄰分段的中心點xj,序列長度減1;(3)計算新生成的段與前后分段的擬合誤差。重復上述過程,直到合并到滿足設定的分段數為止。固定分段數的PLR_BU算法偽代碼如表1所示。 該文提出基于EEMD的固定分段數分段線性表示方法,具體算法步驟如下: 給定時間序列X={x1,x2,…,xn},斜率變化閾值δ,分段數N。 (3)時間序列符號化和確定初始分段段內分段點分布。根據斜率變化將時間序列轉換成由“0”和“1”組成的符號化序列。計算符號化后各初始分段內數據和,得到H={H1,H2,…,HM+1},根據式(10)和(11),得到最終子序列段內分段點分布數量序列C={C1,C2,…,CM+1}。 (4)固定分段數的PLR_BU算法確定最終分段點。根據改進的PLR_BU算法對子序列繼續分段,直到分段數為N,最終分段點序列:X={x1,xi1,…,xiN-2,xn}。 表1 固定分段數的PLR_BU算法 參數說明:在文中方法中,斜率變化閾值δ是主要的參數。設置閾值δ的目的是按照斜率變化過濾數據點,δ值過小時,會將斜率變化相對較小的數據點也轉換為“1”,導致相對平緩的序列段分段點的分布數量也較多;δ值過大時,會將斜率變化相對較大的數據點轉換為“1”,導致只有斜率變化相對較大的序列段分段點的分布數量才會較多。由于P和Q表示相鄰點的差分,所以δ取值范圍為0<δ 該文選擇以下3種時間序列分段線性表示方法作為比較對象。 (1)PAA[6]。 (2)PLR_ITTP[12]。 (3)PLR_TRIP[14]。 X= (12) 式中,t為整數,共600個數據。選擇該仿真序列作實驗,是由于這個序列的重要點比較清晰,且沒有噪聲的干擾,因此,重要點更容易被發現。對序列X加上均值(μ=0)、方差(σ設為0.5~3)、步長為0.5的隨機誤差,對比在不同噪聲的情況下,各個分段方法的抗噪聲能力,檢驗是否可以準確提取全局特征點的有效性,對于對比分析時間序列消除局部最優化問題具有參考意義。 根據仿真數據的實際趨勢,將序列分為13段,將擬合誤差作為評價標準,顯然,提取的分段點越接近原始序列趨勢分段點,擬合誤差越小。實驗結果如圖6和表2所示。 表2 不同噪聲下不同PLR的擬合誤差 圖6是不同噪聲情況下,不同分段方法的分段擬合結果。 圖6 不同噪聲情況下的不同PLR結果 由圖6可知,隨著σ的逐漸增大,分段算法對能夠反映整體趨勢的分段點的識別越來越困難,而文中方法相比于其他3種方法,對該序列中能夠反映整體趨勢的分段點的識別較為準確,尤其在高噪聲情況下更為明顯,而其他3種方法均提取了錯誤的分段點。 由表2知,文中方法雖受噪聲干擾,但總的來說,抗噪聲干擾的能力比其他3種方法有所加強,可以非常準確地提取反映整體趨勢的分段點,而其他方法則極易受到噪聲的干擾,導致陷入局部最優狀態。 由圖6和表2可知,盡管噪聲的增加對PAA的擬合誤差影響較小,但其整體的擬合誤差相對較大,這是由于PAA采用等長分段,分段點的選取不會受到噪聲的影響。而PLR_ITTP、PLR_TRIP都通過某種抗噪機制削弱了噪聲的干擾,使得擬合誤差相對較小。PLR_ITTP在噪聲較低時,擬合誤差較小,但在噪聲較高時,擬合誤差隨之變大,這是因為PLR_ITTP只重視時間序列的局部特征,而忽略了全局意義下的時間轉折點,這將導致在高噪聲的時候,算法會錯誤地提取關鍵點。PLR_TRIP在不同噪聲下擬合誤差都較大,并且出現了震蕩上升的情況,由于PLR_TRIP的角度閾值和趨勢段閾值的組合選取是復雜的,不同的閾值組合會造成擬合誤差的大幅變化,同時PLR_TRIP提出趨勢段的概念來削弱噪聲的干擾也是只關注局部信息。而文中方法先通過模態重構方法得到全局分段點,使得文中方法有效克服上述方法存在的局部最優化缺陷,之后使用自底向上方法進行融合,保留了基于分段誤差的分段算法擬合誤差較小的優點。 壓裂施工過程中,通過記錄不同時間段的施工壓力、泵注排量和加砂體積分數獲得壓裂施工曲線,有效利用壓裂施工曲線并提取有效信息,不僅能夠對儲層及裂縫參數再認識,而且對于指導壓裂施工以及調整壓裂設計方案、提高壓裂技術水平和施工效果有重要的借鑒作用。因此,對壓裂施工曲線的挖掘和分析有著重要的工程意義和應用價值[22]。但壓裂施工曲線是一種高維數據,為了方便后續存儲和挖掘需要對其進行壓縮表示。該文選用某區塊的壓裂施工數據,時間間隔為1 s,共2 500個數據值。 為了比較文中算法與其他算法的優劣,并考慮到實際壓裂施工曲線的高維性特點,將考察所有方法在壓縮率分別為90%、92%、94%、96%、98%時的擬合誤差,實驗結果如圖7所示。 圖7 壓裂施工曲線不同壓縮率下的擬合誤差 由圖7可知,文中方法在不同壓縮率下的擬合誤差都是最小的,優于其他3種方法。 圖8 96%的壓縮率下不同方法分段擬合效果對比 由圖8可知,對壓裂施工時間序列這種高噪聲且分布復雜的序列進行趨勢提取時,PLR_ITTP、PLR_TRIP因存在局部最優化的問題而導致“漏提取”“過提取”現象較為嚴重,丟失了反映整體趨勢的重要點;而文中算法能夠有效地去除時間序列中的噪聲,準確提取反映時間序列整體趨勢的分段點。 針對現有方法的不足,該文提出一種基于EEMD的固定分段數表示方法。仿真實驗結果表明:該方法的擬合誤差分別比PAA、PLR_ITTP、PLR_TRIP平均減小了80%、59%、78%,其有效地解決了現有分段方法存在的問題,極大地削弱了噪聲干擾,從而能夠準確地找到反映整體趨勢的分段點。最后將該方法應用于壓裂施工數據,其擬合誤差分別比PAA、PLR_ITTP、PLR_TRIP減小了86%、84%、89%,再次證明了所提方法對趨勢提取的有效性和準確性。1.2 問題描述
2 集合經驗模態分解和改進的自底向上分段
2.1 集合經驗模態分解
2.2 IMF重構

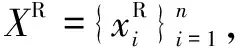
2.3 時間序列符號化
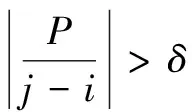
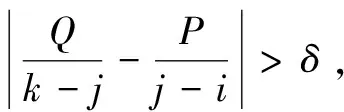

2.4 固定分段數的自底向上分段
2.5 時間序列分段線性表示方法
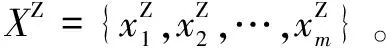
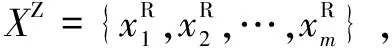

3 實驗與分析
3.1 實驗對比方法
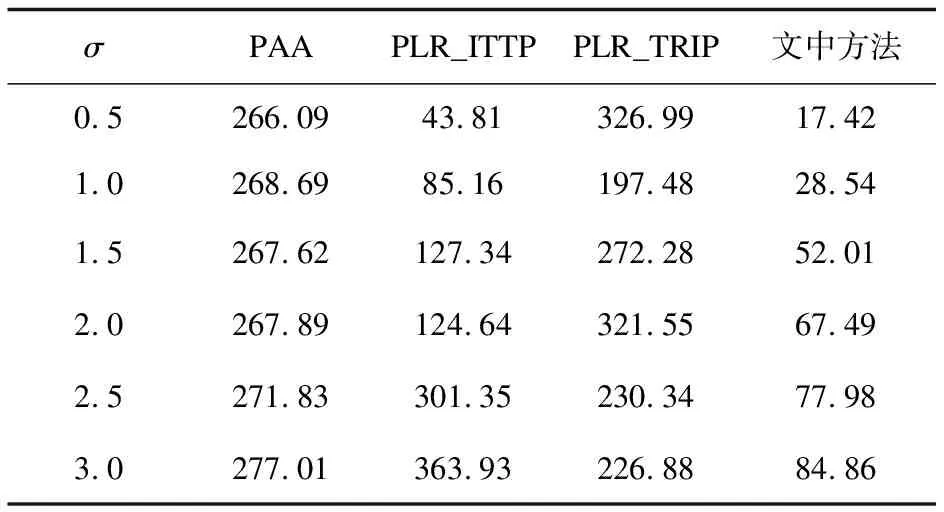
3.2 仿真數據驗證
3.3 工業實例應用
4 結束語

