基于預測變異多目標粒子群算法的風-光-抽水蓄能系統日前調度

羅 毅，張 巖

（華北電力大學 控制與計算機工程學院，北京 102206）

0 引言

在國家“碳達峰、碳中和”目標的背景下，風能、太陽能等可再生能源得到快速發展[1]。然而，風力和光伏發電的隨機性和間歇性對微電網協同運行提出了挑戰，增加了調度成本[2]。因此，需要儲能裝置來保證系統穩定運行。

抽水蓄能電站以其技術成熟、存儲效率高、調峰能力強而得到廣泛應用[3]。風-光-抽水蓄能優化調度是一個高維、非線性、多約束問題[4]。粒子群算法（PSO）因原理簡單、搜索能力穩健等特點而備受關注。目前，粒子群算法在單目標優化方面研究已經較為成熟，但在工程實踐中，多目標往往更能確切反映微電網實際運行狀態[5]，同時多個目標之間往往存在沖突。文獻[6]以燃料運維成本最小、污染物排放最少和切負荷補償成本最小為目標，使用改進的混沌粒子群算法進行求解。文獻[7]以風電消納電量最大和火電發電成本最小為目標函數，采用基于混沌變異的改進粒子群算法進行求解。以上文獻在建立模型時，通過加權或者模糊化的方法，將多目標優化問題轉換為單目標優化問題，各目標之間的平衡關系無法保證，且主觀性較強。文獻[8]提出了多目標粒子群算法（MOPSO），使用非支配排序和超立方體技術將粒子群算法擴展到多目標問題。多種改進的MOPSO被提出并廣泛應用于能源和電力系統中。文獻[9]提出了基于優先排序和多子群協同進化的MOPSO，并應用于含大規模風電的電力系統負荷分配方面，但其采用的多目標分解策略，基于權重向量來指導種群進化，對于具有復雜Pareto前沿的問題，不能保證解的均勻分布性。文獻[10]提出了基于擁擠距離的稀疏度排序法的MOPSO，并應用于電力系統環境經濟調度方面。雖然擁擠距離法能較好地反映粒子間的擁擠程度，但其相應的優化結果的多樣性不足，全局搜索能力較差[11]。文獻[12]以煤耗成本最小和污染物排放最少為目標，采用基于目標權重導向的MOPSO進行優化調度，在解的多樣性和求解速度上有一定優勢，但是缺少評價多樣性的指標。

本文提出一種基于預測變異的多目標粒子群算法（P-MOPSO），根據迭代時粒子歷史位置和粒子當前位置，計算預測的粒子平移向量，并沿預測方向進行變異操作，增加種群的多樣性，與傳統擁擠距離稀疏度排序的MOPSO算法相比，具有更好的全局搜索能力。引入分散度指標衡量多樣性和收斂性，相較于多子群協同進化的MOPSO，具有更快的求解速度。將P-MOPSO算法應用于風-光-抽水蓄能聯合發電系統，制定最優日前運行計劃，使運行收益最大化的同時，與電網交互功率波動最小。

1 風-光-抽水蓄能聯合發電系統優化調度模型

風-光-抽水蓄能聯合發電系統網絡結構如圖1所示。

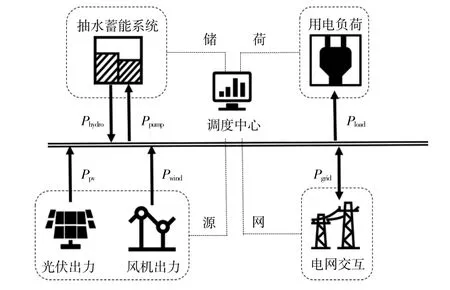
圖1 風-光-抽水蓄能聯合系統拓撲結構圖Fig.1 Topological diagram of wind-solar-pumped storage system

該系統由風機、光伏組件、抽水蓄能系統組成。本文假設已知調度周期內的風機預測出力、光伏預測出力和負荷預測值。以抽水蓄能系統出力、電網交互功率為優化變量，在滿足各單元運行約束且考慮棄風棄光的條件下，使系統的經濟效益最大，同時減小電網交互功率波動。

1.1 抽水蓄能系統模型

抽水蓄能電站是一種技術較為成熟的中間存儲系統，能夠起到削峰填谷的作用。本文建立了可變速抽水蓄能機組模型。相較定速機組，可變速抽水蓄能機組可以在抽水狀態實現功率調節，在發電狀態具備更寬的功率調節范圍[13]，[14]。抽水和發電工況下抽水蓄能電站具體數學模型如下。

1.1.1水泵運行模式

當風光出力大于負載所需，且向電網售電價格較低時，可利用水泵抽水到上水庫儲存。抽水功率與水量變化表達式為

式中：Ppump為抽水功率；ρ為水的密度；g為重力加速度；ηp為水泵工作在額定功率附近的效率；ΔQp為泵流量，m3；Δh為水柱高度變化量，m；Δt為調度時間間隔。

1.1.2水輪機運行模式

當風光出力小于負載需求時，可利用上水庫中儲存的水帶動水輪機發電。水力發電系統的發電量與水量變化為

式中：ηh為渦輪循環的效率；ΔQh為渦輪流量，m3。

1.1.3上水庫蓄水量

式中：Spump，i為第i時段水庫的蓄水量，m3；δ為單個時段內水庫因蒸發和滲漏而損失的水量。

1.2 目標函數

在并網模式下，微電網以滿足負載需求為首要目標，多余電量存儲或上網，不足電量從電網購買，目標函數定義如下。

1.2.1綜合收益最大

式中：T為全天時段數；fRE，i，fPH，i和fGR，i分別為第i時段可再生能源發電收益、抽水蓄能運行收益和與電網交互綜合收益；Pwind，i，Ppv，i，Pwaste，i分別為第i時段風機功率、光伏功率與棄風棄光總量；Cw，i為棄風棄光懲罰費用；Csell，i為第i時段售電價格；Pbuy，i為第i時段從電網購電量；Cbuy，i為第i時段從電網購電價格；Phydro，i，Ppump，i分別為第i時段水輪機發電功率、水泵抽水功率；Cpump，i為水泵抽水等效電價，取為0.25Csell，i；counti為第i時段機組是否有啟停動作；Cost為機組單次啟停費用。

1.2.2電網交互功率波動最小

式中：Pgrid，i為第i時段與電網交互功率。

1.3 約束條件

①系統功率平衡約束

式中：Pload，i為第i時段預測的負荷需求，忽略網絡傳輸損失。

②各子系統出力上下限約束

本文采用可變速抽水蓄能機組，為保證其運行效率，約束在抽水工況下，工作在70%～100%最大功率內，發電工況下，工作在20%～100%最大功率內[15]。

③電網交互功率約束

④上水庫庫容約束

⑥起止時刻水庫蓄水量的變化范圍約束

式中：Spump，T0，Spump，Te分別為調度初時刻和末時刻的上水庫蓄水量。

2 改進的P-MOPSO求解日前調度問題

2.1 標準多目標粒子群算法（MOPSO）

MOPSO以傳統的自然啟發算法PSO為基礎，模擬多個生物的行為，它們根據搜索空間中某一給定時刻所發現的局部和全局最佳位置移動。在初始化階段，在搜索空間內隨機生成種群，并初始化外部檔案A。每個粒子i表示為一個數值向量，在每次迭代過程中，其速度Vi和位置Xi不斷更新，ω為慣性權重，通常取0.4；r1，r2為0～1均勻分布的隨機數；c1和c2分別為個人認知因子和社會認知因子；Pi為粒子i到當前迭代為止的個體最優位置；Gi為從外部檔案中獲取的主導粒子。

2.2 對MOPSO的改進

針對MOPSO所存在的問題，如全局搜索能力較差、多樣性無法保證和收斂速度較慢等，采取以下措施進行改進。

2.2.1多樣性改進

采用基于預測的變異策略（P-MOPSO），在整個迭代過程中分段實施預測變異：在第t次迭代中，根據第t-1次迭代時粒子位置和粒子當前位置，計算預測的粒子平移向量，然后沿著預測方向變異來提高種群的多樣性。

式中：ωij≥0指定提供的信息對的預測向量的貢獻，越接近的解對的貢獻越大[16]，其計算方法為

式中：dij為歐氏距離；為基準距離。

2.2.2收斂準則的改進

本文提出兩個指標來判斷外部檔案粒子多樣性以及是否滿足收斂準則。

①分散度S

②擁擠距離的均方根Eq

式中：N為點的個數；α為帕累托邊界的極值在連續兩次迭代中的變化量；d為擁擠距離；為擁擠距離的算術平均值；σ為擁擠距離的標準差。

分散度S綜合反映了迭代過程中Pareto前沿的分布與變化趨勢，S越大，粒子多樣性越好；Eq是對外部檔案粒子擁擠距離的擬合[17]。當檢測到迭代過程中分散度與擁擠距離連續M次（M為設定值）變化量低于一定閾值時，表示算法已經得到了可靠的Pareto前沿，因此本文改進的迭代結束條件：①達到最大迭代次數；②分散度變化小于給定值；③擁擠距離的均方根變化小于給定值。

改進后的多目標粒子群算法流程見圖2。

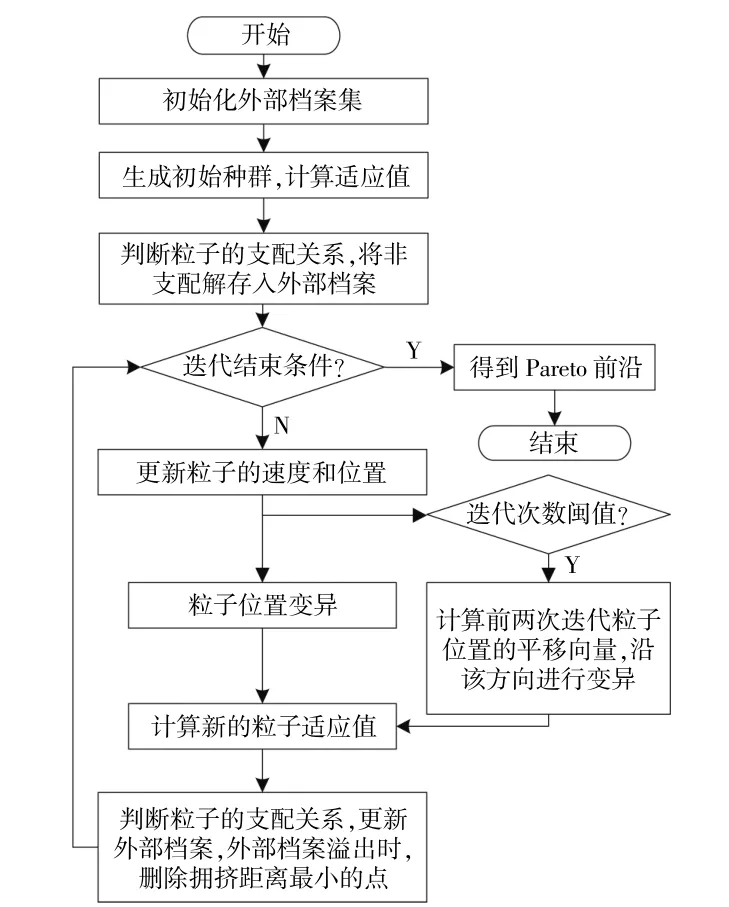
圖2 P-MOPSO流程圖Fig.2 Flowchart of P-MOPSO

2.3 Pareto解集中的選擇策略

由于目標之間存在沖突和無法比較的現象，在改進某一目標函數的同時，必然會削弱另一個目標函數。因此多目標優化得到的是一個Pareto解集，為決策者提供了多種選擇方案。對于實際問題，在選取最終方案時要考慮多方因素，本文對外部檔案的處理策略如下：

①剔除異常值；

②在保證多樣性的基礎上，為調度人員提供多種決策方案；

③在無人決策的情況下，采用基于隸屬度的模糊綜合評價方式自動決策，選用降半Γ形分布，建立各目標的隸屬度函數[18]：

u∈[0，1]反映了對每個目標的滿意度，其值越大表示對該目標越滿意。基于目標滿意度對算法求得的多個解進行歸一化加權，選擇折衷解：

式中：β為折衷系數，其值為滿足運行約束條件下，隸屬度函數交集中的最大值。

3 仿真驗證

3.1 參數設置

本文研究一個500 MW風電場、250 MW光伏電站和200 MW抽水蓄能電站構成的并網聯合發電系統，系統結構見圖1，抽水蓄能電站參數如表1。考慮到線路傳輸能力限制，與電網交互的最大功率為200 MW，日前調度周期為1 d的24個時段，圖3為參照已有的典型日出力預測[6]，模擬得到的日負荷曲線以及風光出力曲線。考慮如圖4的分時電價，分別采用MOPSO和P-MOPSO算法進行仿真驗證。

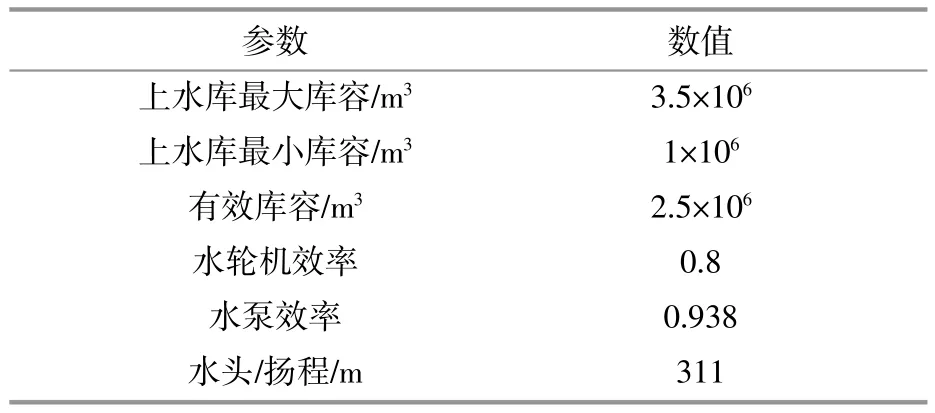
表1 抽水蓄能機組參數Table 1 Parameters of pumped storage unit

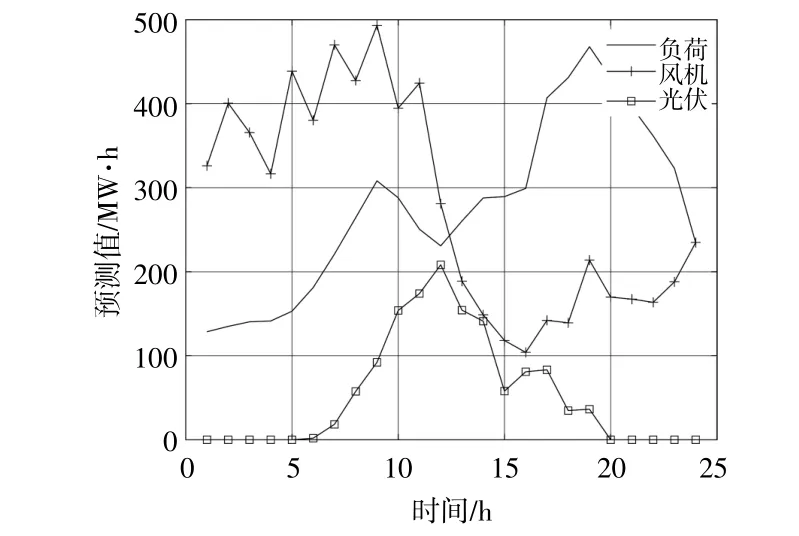
圖3 日負荷、風機、光伏出力預測值曲線Fig.3 Predicted value curves of daily load，fan and photovoltaic output

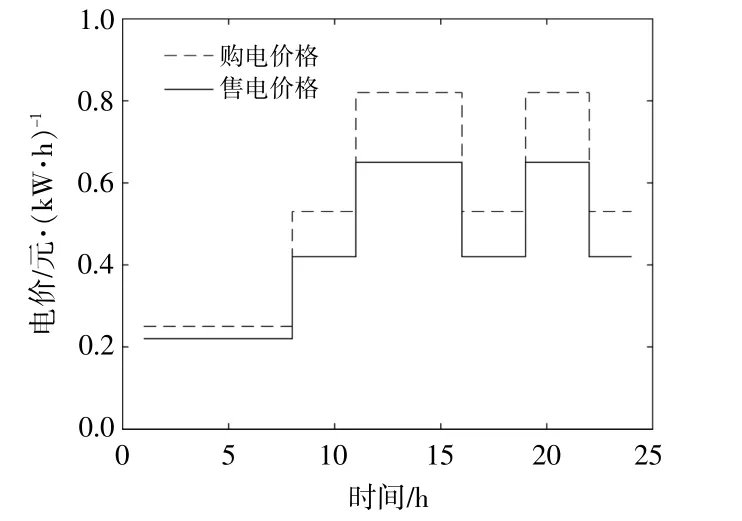
圖4 分時購售電價階梯圖Fig.4 Time-segments electricity price ladder diagram

3.2 調度結果

設置最大迭代次數為300，種群規模為1 000，外部檔案最大存儲粒子數為100。采用MOPSO和P-MOPSO分別求解問題10次，目標函數值、性能參數結果如表2所示。

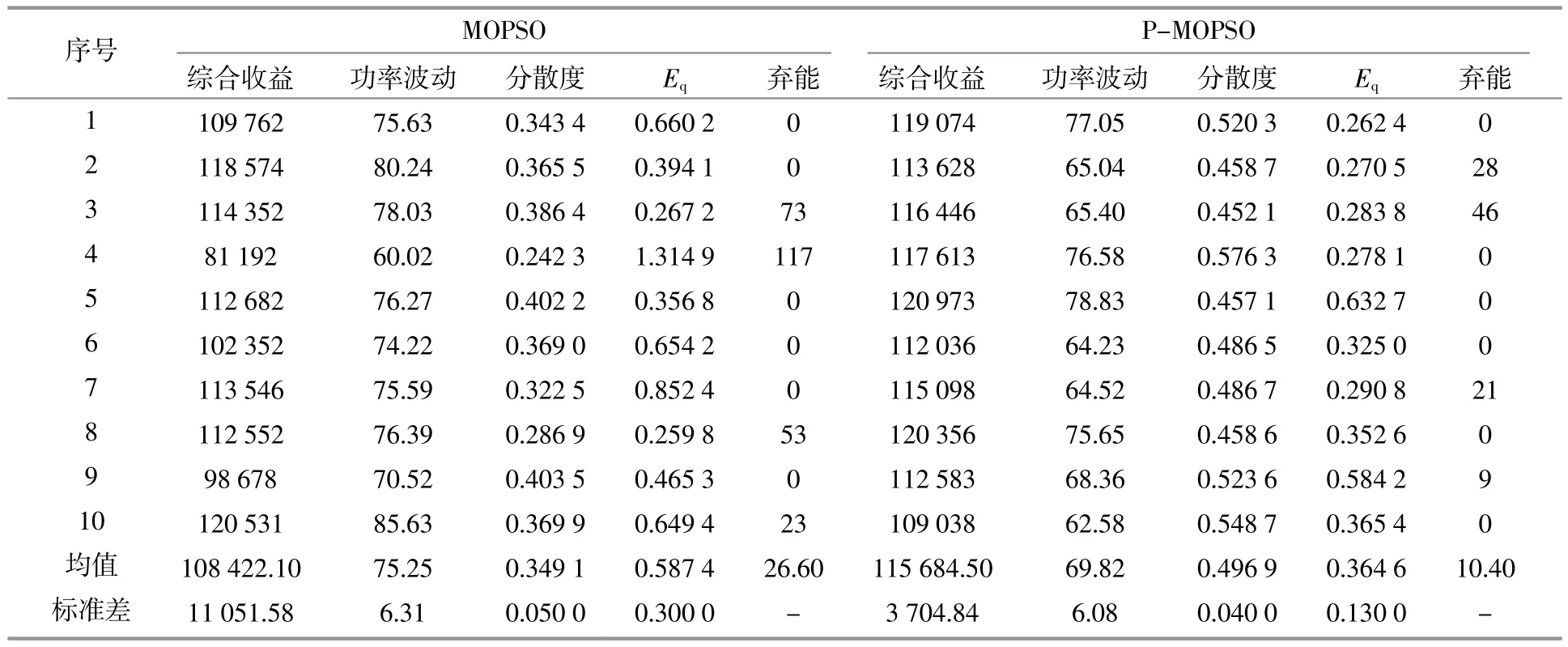
表2 算法改進前后的求解結果Table 2 Solution results before and after algorithm improvement

由表2可知，在算法性能上，MOPSO和P-MOPSO的平均分散度分別為0.349 1，0.496 9，即P-MOPSO的整體分散度較高，粒子的多樣性更好。并且，從多次運算的結果來看，MOPSO多次計算所得各項結果的標準差較大，即在算法穩定性上P-MOPSO比MOPSO更具優勢。在可再生能源消納上，10次典型調度方案中有6次全部消納，同時在棄能的情況下，P-MOPSO的平均棄能水平低于MOPSO；在平抑功率波動上，MOPSO和P-MOPSO調度結果的電網交互功率標準差均值分別為75.25和69.82，即P-MOPSO的功率波動較小，同時總出力曲線與負荷曲線擬合程度更好，證明改進的算法更加適配風-光-抽水蓄能聯合發電系統調度模型，具有更高的能源利用率。

選取折衷解作為典型調度結果進行圖示分析，改進前后的Pareto前沿如圖5所示。各子系統出力情況如圖6所示。

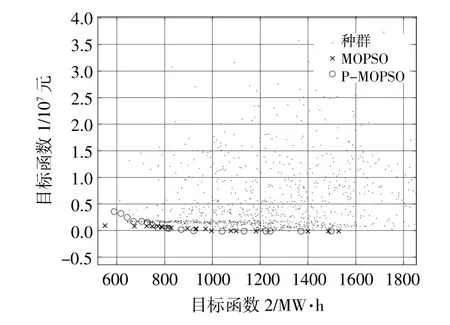
圖5 Pareto前沿對比Fig.5 Pareto frontier comparison chart

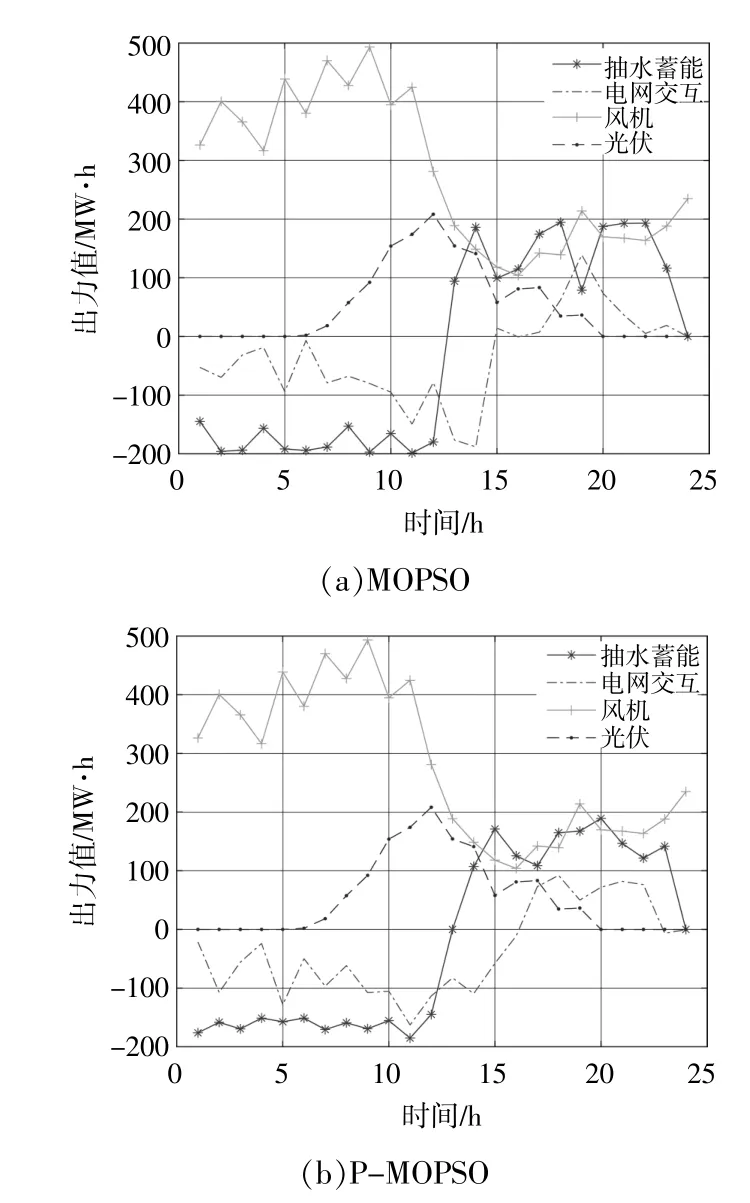
圖6 各子系統出力曲線Fig.6 Sub-system output curve

由圖5可知，在迭代過程中，MOPSO和PMOPSO均能搜索到接近真實的Pareto前沿，但P-MOPSO的Pareto前沿分布更加均勻，多樣性更好。另外在求解時間上，MOPSO平均求解用時296 s，而P-MOPSO平均求解用時94 s，收斂速度更快。結合圖4，6可知：在電價較低或風光出力溢出較多時，溢出部分用于水泵抽水，綜合考慮收益與功率波動，必要時進行棄風和棄光；在電價較高或風光出力不足時，抽水蓄能以發電工況運行滿足負荷需求。此外，MOPSO和P-MOPSO計算得到的出力計劃與電網交互功率標準差分別為78.03和65.40，綜合收益分別為11.44萬元和11.64萬元，P-MOPSO的調度曲線更加平滑，充分發揮了抽水蓄能電站削峰填谷和減小電網交互功率波動的作用。

圖7為初始蓄水量均為1.5×106m3的情況下，MOPSO和P-MOPSO調度結果。

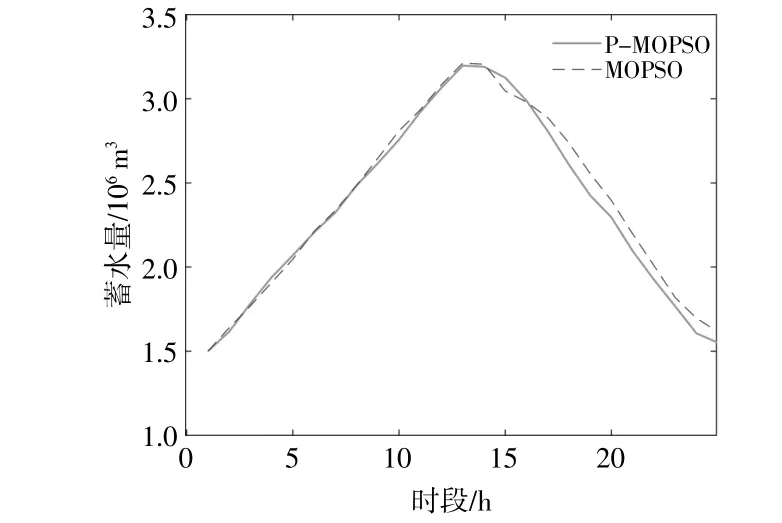
圖7 庫容變化對比曲線Fig.7 Comparison curve of storage capacity change

由圖7可知，日運行最大蓄水量分別為3 211 908，3 196 574 m3，末時刻蓄水量分別為1 615 138，1 550 887 m3，在首末時刻蓄水量的變化量上，PMOPSO的調度結果更加符合抽蓄電站連續運行約束。另外，在運行過程中，在庫容限制的基礎上考慮了抽水蓄能機組能夠提供的正負旋轉備用（有效庫容的10%），以應對可再生能源預測出力以及負荷預測的不確定性。

4 結論

本文研究了風-光-抽水蓄能聯合發電系統的日前優化調度問題。采用基于預測變異的多目標粒子群算法確定最優抽水蓄能運行方式、電網交互功率，以實現最大化綜合收益和最小化電網交互功率波動的目標。仿真結果表明：P-MOPSO算法在解的多樣性和收斂速度上更加具有競爭力，且穩定性更強；采用P-MOPSO算法進行風-光-抽水蓄能系統優化調度可以顯著提高系統的綜合收益。