基于MPC算法的風電參與頻率調控策略

段家華，姚 樸，姚金明

（1.云南能投新能源投資開發有限公司，云南 昆明 650032；2.國電南瑞科技股份有限公司，江蘇 南京211100；3.南京郵電大學 自動化學院 人工智能學院，江蘇 南京 210023）

0 引言

隨著“碳達峰”和“碳中和”的不斷推進[1]，[2]，風力發電已得到了廣泛的應用和發展[3]，[4]。然而，由于風力的隨機性和波動性，且風機不具備頻率響應能力，大規模風機并網會對電力系統頻率穩定性造成威脅[5]，很大程度上制約了風電的消納。

傳統發電機組通過轉子速度對系統頻率變化的響應來調節系統頻率。雙饋風力渦輪機在最大風能跟蹤模式下運行，如果沒有額外的頻率控制鏈路，則無法參與系統頻率調制。風電機組頻率控制策略主要分為轉子慣性控制、下垂控制、減載控制3種類型[6]。文獻[7]通過提出的頻率控制策略驗證了在有功率備用時，風機能夠參與系統頻率調節。文獻[8]基于傳統下垂控制進行自適應調整，提高了風機頻率響應能力，但是依賴風機風速超短期預測精度。文獻[9]通過下垂控制，讓DFIG有效地模擬同步機的有差調節特性，最終達到新的穩態平衡工作點。文獻[10]引入了慣性控制的方法，即通過在系統頻率模塊加入控制環節，釋放風機轉子動能參與系統的調頻，使風力發電機等效為同步發電機，并對外界負載進行慣性響應。文獻[11]對下垂系數以及虛擬慣性參數進行整定后，配合槳距角控制方式，使風機參與不同風速段的調頻，提升了協調控制的調頻效果。現有頻率控制方法大多假設通信系統能夠實現無延遲丟包的實時控制，而不考慮調頻過程中通信時延的影響。在實際情況下，在風電機組參與電力系統的調頻輔助過程中，通信信道將產生時間延遲。文獻[12]，[13]分析了雙饋異步電機參與的風電并網時，存在時滯對含風電機組的電力系統穩定性的影響。文獻[14]建立了考慮控制延時環節的風電參與調頻狀態空間模型，并采用特征值分析方法分析系統穩定性。由以上分析可以看出，在頻率調節時，通信延遲對系統動態響應有一定負面影響。目前，很多工作主要集中在基于理論分析時延對穩定性和收斂性的影響，而如何消除時間延遲造成的不利影響的研究相對較少。

本文提出了基于MPC算法的風電調頻延時補償控制策略。針對風電參與調頻的電力頻率響應模型，設計了基于MPC的狀態空間動態模型，優化風電綜合慣量控制參數，并設計了MPC優化目標函數，實現對預測值不斷地更新校正，使風機獲得最優控制參數；考慮MPC主控制器發出的指令信號與本地控制器之間的時間延遲和丟包，通過建立控制信號的選擇規則，在預測模型的滾動優化過程中對多步控制信號進行動態調整，形成考慮延時和丟包的延遲補償機制；并通過Matlab/Simulink仿真對所提出的控制器模型和補償策略的性能進行了評估，驗證了該補償策略的有效性，表明該補償策略可以提高風電機組參與調頻對通信延時的魯棒性，提高風電并網的頻率支撐能力。

1 含DFIG的系統頻率響應模型構建

1.1 DFIG模型

DFIG以變速恒頻方式運行。風力電機將風能轉化為機械能，其葉片形狀和曲線按照空氣動力學原理設計而成。風力機從風能中所吸收的功率Pwind為

式中：Cp為風能利用系數；ρ為空氣密度；S為葉片掃掠面積；Vm為風速。

當風電機組以虛擬慣性和下垂控制組合的方式參與系統調頻時，雙饋風機慣性控制模型如圖1所示。

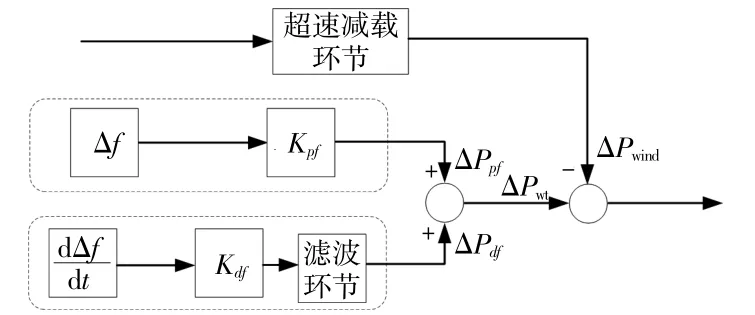
圖1 風電調頻功率回路Fig.1 Wind power frequency modulation power circuit diagram

圖中，利用比例下垂控制進行慣性控制增加的額外功率ΔPpf，利用微分比例控制釋放（吸收）部分旋轉動能而改變電磁功率ΔPdf，其表達式分別為

1.2 系統頻率響應模型

圖2為本文所提的系統頻率響應模型，該模型包含傳統頻率響應模型及MPC下的DFIG模型。

圖2 含DFIG的系統頻率響應模型Fig.2 System frequency response model with DFIG

圖中：H，D，R分別為等效慣性時間常數、系統阻尼系數和電力系統的調速系數；Tg和Tt分別為調速器與渦輪機的時間常數；u1，u2分別為Kpf和Kdf的控制信號；Δf，ΔPg分別為頻率偏差和調速器位置的變化；ΔPwt和ΔPt分別為雙饋風機和渦輪機的總輸出功率變化；ΔPL為負荷擾動；α1和α2分別作為頻率偏差對主控制器和雙饋風機控制器的分配系數，α1+α2=1。

等效調速器、渦輪機、DFIG、電力系統的頻率動態響應分別為

式中：ΔP1為風電調頻輔助變量。

2 基于模型預測控制的風電一次調頻策略

2.1 預測模型

電力系統的狀態空間動態頻率模型為

式中：x（t）∈Rn為狀態向量；u（t）為綜合慣量控制參數的控制向量；y（t）為系統輸出向量；w（t）為干擾向量，定義：

根據式（3）～（6）得到系統矩陣A、控制矩陣B、輸出矩陣C和干擾矩陣F分別為

定義預測范圍Np和控制范圍Nc，且Nc≤Np。基于離散化公式，在時間k處推導預測模型為

式中：

根據上述公式，可通過以下預測方程計算系統的未來輸出：

式中：

2.2 滾動優化

將頻率偏差的參考值設置為零，以下目標優化問題的控制信號。

式中：

通過求解式（15），得到最優控制序列為

3 風電調頻延遲補償策略

在實際的頻率響應控制系統中，通信傳輸時，一般存在由設備的位置、信號傳播速度等主要影響因素導致的通信延時。由于通信網絡中存在延時，原本已標定的物理系統性能衰退，嚴重時導致系統失穩。在本節中，考慮到抵消輸入延遲的影響，使用基于MPC方法的主動補償控制策略來進行補償。本文所提基于MPC的調頻延時補償控制流程如圖3所示。

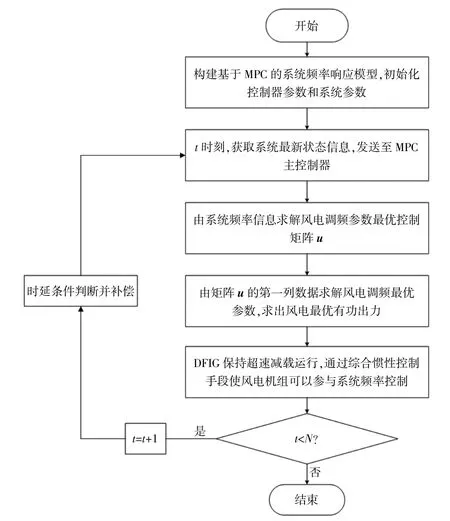
圖3 基于MPC的風電調頻延時補償控制流程圖Fig.3 Flow chart of wind power frequency modulation delay compensation control based on MPC

4 仿真結果與分析

基于上述分析，本節利用Matlab/Simulink建立5機14節點模型進行驗證。該系統包含5臺額定功率為600 MW的同步發電機G1，G2，G3，G4，G5。用一個額定容量為900 MW的等值DFIG替換其中的一臺機組G5，建立含DFIG的系統頻率響應仿真模型，如圖4所示。設DFIG的額定風速為10 m/s，低風速為7 m/s，仿真時間t=20 s，系統在t=0.1 s時發生負荷突增200 MW。本文分別對含DFIG的系統頻率響應進行分析，并假設DFIG的運行參數、環境參數均相似，等值模型見圖2，利用Matlab/Simulink進行仿真分析。本文將MPC方法應用到含風電電力系統頻率控制中，考慮風速、延時和負荷擾動情況，協調優化常規機組與風電機組，減小偏差。該方法可以維持系統頻率及區域間交換功率在較小的范圍內變化，控制效果明顯優于常規負荷頻率控制器。

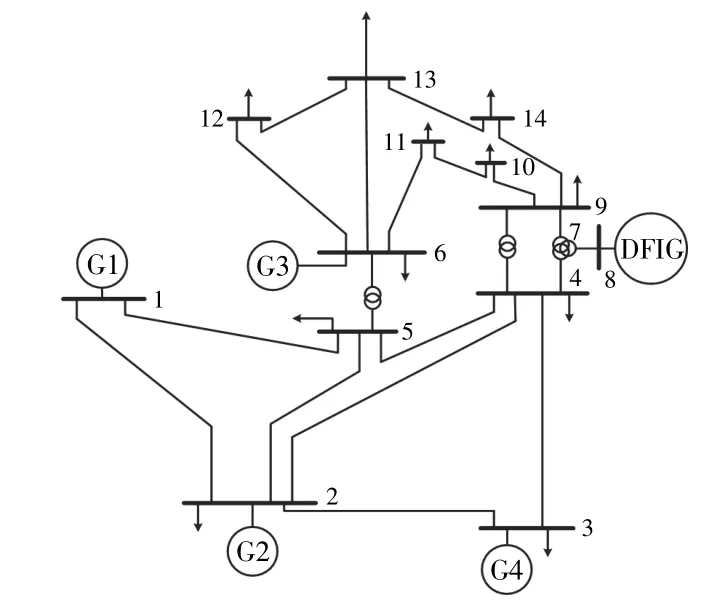
圖4 5機14節點系統模型Fig.4 5-machine 14 node system model

4.1 參與動態響應的DFIG對系統頻率穩定性的影響

本文針對含DFIG的電力頻率響應模型，設計了基于MPC的狀態空間滾動優化模型，并探討通信延時的影響。本節討論了3種情況下不同風電參與調頻占比α1和傳統機組參與調頻占比α2對系統頻率的影響。在0.025 p.u.的階躍擾動下，情況1：α1=1，α2=0；情況2：α1=0.8，α2=0.2；情況3：α1=0.5，α2=0.5。

圖5描述了不同風電參與調頻占比下的系統頻率響應。

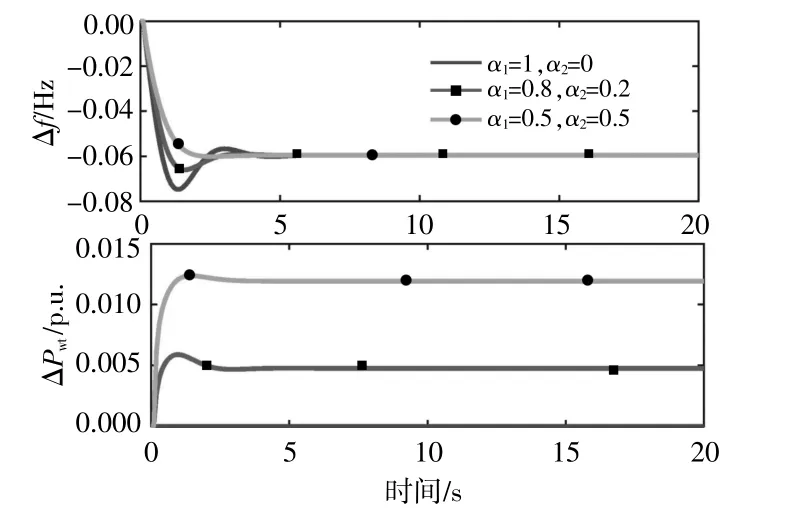
圖5 不同風電參與調頻占比下的系統頻率響應對比Fig.5 Comparison diagram of system frequency response under different wind power participation frequency modulation proportion

由圖5可知，與情況1相比，有風電參與調頻的情況2和3對改善頻率響應具有積極影響。此外，在不改變風電裝機容量的前提下，提高風電參與調頻占比，即將情況3與情況2相比，系統頻率偏差不再振蕩，頻率偏差下降趨于平穩，這表明風電參與系統調頻的比重越大，頻率響應性能也會進一步得到改善。

4.2 不同控制策略對風電參與電力系統頻率響應影響

為了驗證本文提出的系統頻率控制方法的有效性，分別評估了在恒風速和變風速情況下，采用不同的調頻控制策略對風電機組參與電力系統頻率調節的影響。當采取綜合慣量控制方式時，設參數Kpf為20，Kdf為8。為了更加明晰本文所提控制策略對系統頻率的控制效果，參與動態響應的DFIG占比參考情況3，并假設階躍擾動增量為0.025 p.u.，仿真結果如圖6所示。

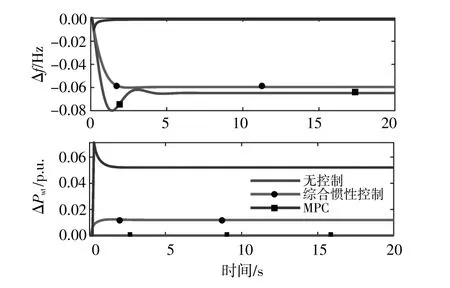
圖6 常風速條件下的系統動態響應對比Fig.6 Comparison diagram of system dynamic response under constant wind speed

由圖6可知：在風速恒定的場景下，當DFIG不參與調頻時，系統頻率偏差急劇下跌，出現較大的超調量；當采取綜合慣性控制方式時，系統頻率下降趨勢較平穩，最終頻率誤差略有減小，風電參與調頻的功率水平也較低。在本文控制策略下，系統頻率僅略微下降，之后快速恢復并一直保持在50 Hz。相較于綜合慣性控制方式，本文所提策略下的最大頻率誤差有顯著減小，同時風電參與調頻的功率水平也明顯提高。

在變風速場景下，系統動態響應如圖7所示。

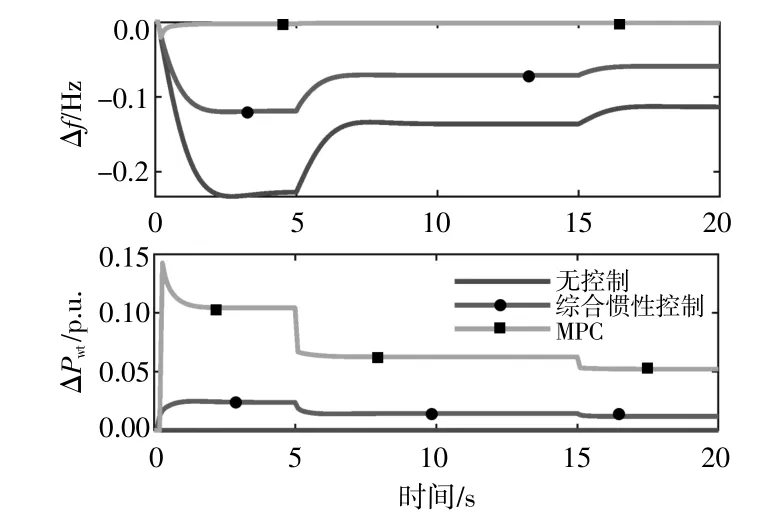
圖7 變風速條件下的系統動態響應對比Fig.7 Comparison diagram of system dynamic response under variable wind speed

由圖7可知，無控制策略和綜合慣性控制策略下的頻率波動明顯增大，但本文所提控制策略下的系統頻率誤差和風電調頻出力，相比其他兩種控制策略仍然保持著較穩定的水平。

采用本文所提的控制策略，無論是恒定風速還是變風速場景下，頻率偏差較小，頻率更快速的達到穩定狀態。這表明了本文所提出的控制策略的優勢。

4.3 通信延時對電力系統頻率響應的影響

考慮到MPC主控制器發出的指令信號與本地控制器之間存在時間延遲和丟包的情況，本文建立含延時的電力頻率響應模型，并評估不同延時對系統的影響。參與系統調頻的風電參與調頻占比α2參考情況2，并同樣設階躍擾動增量為0.025 p.u.。為了測試通信延時對系統產生的影響，引入了不同的通信定時延值，系統頻率和風電調頻出力的動態性能如圖8所示。

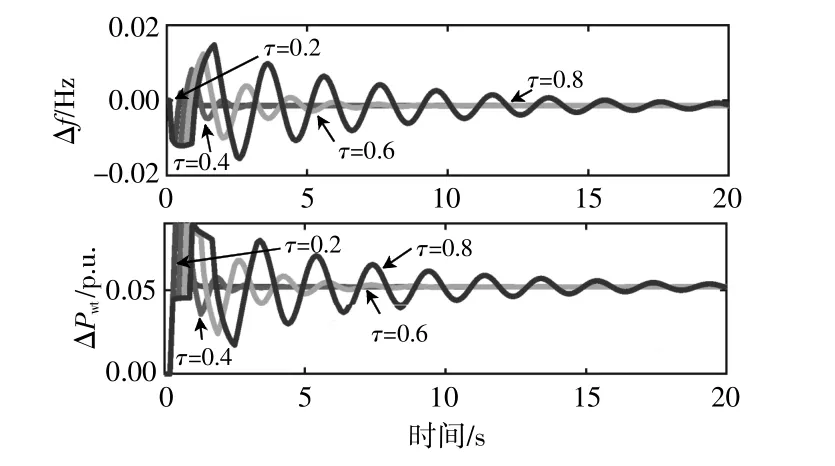
圖8 考慮不同通信延時下系統動態響應對比Fig.8 Comparison diagram of system dynamic response considering different communication delay

隨著時延的增加，頻率偏差也明顯逐增。通信延遲對電力系統的頻率響應產生負面影響，當通信延遲不斷增大超過一定閾值時，電力系統性能會逐漸惡化，出現衰減振蕩趨勢。但在本文所提的控制策略下，系統頻率偏差仍保持在一定范圍內，且能保證系統在較短的一段時間內恢復穩定，這也表明了本文所提延時補償策略的有效性。

4.4 有無延遲補償的系統性能對比效果

隨著越來越多的新能源機組接入電力系統，電力系統出現低慣量特性，容易導致頻率不穩定，影響頻率調節的效果。為了驗證本文所提出的控制方法的魯棒性和延遲補償策略的有效性，圖9，10對恒定風速、不同延時情況下，有無延遲補償時系統的頻率響應和輸出功率進行對比。為系統提供的風電滲透率參考情況2，并設階躍擾動增量為0.025 p.u.，定風速Vm為7 m/s。

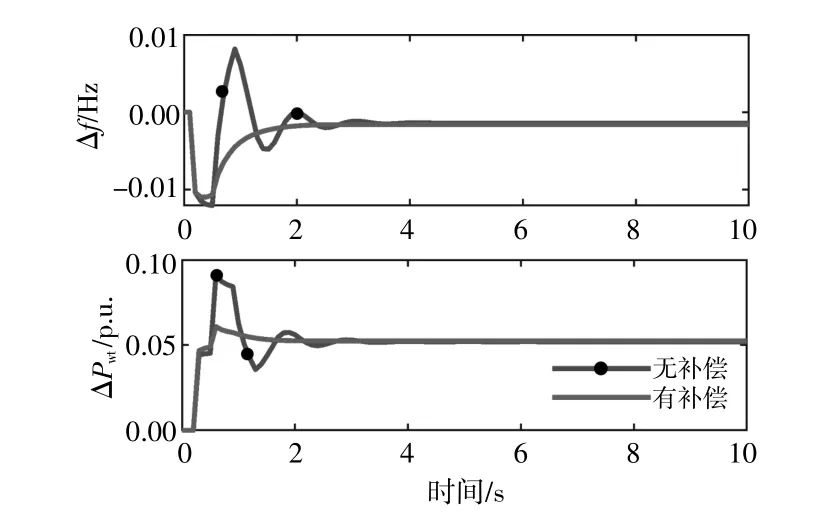
圖9 τ=0.4 s有無預測補償的系統動態響應對比Fig.9 Comparison diagram of system dynamic response with or without predictive compensation at τ=0.4 s

由圖9可知，當時延τ=0.4 s時，有補償的系統比沒有補償的系統更快穩定，說明了時延補償策略的有效性。

由圖10可以看出，當向系統引入延時τ=0.8 s而沒有延遲補償時，系統產生衰減振蕩，長時間無法達到穩定。可以觀察到，當系統由于通信延遲的影響而不穩定時，延遲補償方法提供了更好的性能，系統動態性能沒有進一步惡化。

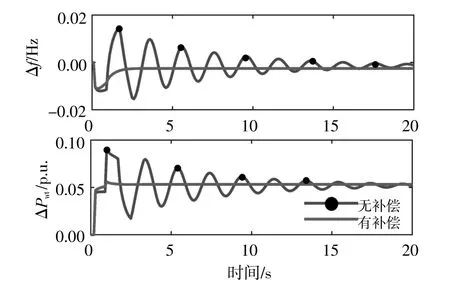
圖10 τ=0.8 s有無預測補償的系統動態響應對比Fig.10 Comparison diagram of system dynamic response with or without predictive compensation at τ=0.8 s

在實際情況中，風速不是恒定不變的。變風速影響下，DFIG的輸出功率也會產生波動。為了驗證本文所提出的控制方法的魯棒性和延遲補償策略的有效性，考慮變風速情況下的系統頻率誤差和DFIG輸出功率。使用情況2的參數，并假設出現與之前同樣的階躍負載擾動，設置初始風速V=7 m/s，在t=5 s時，風速突增至10 m/s，持續10 s，在t=15 s時風速突增至12 m/s，持續至20 s，如圖11所示。

圖12，13為在變風速情況下，有延遲補償和無延遲補償時頻率響應和功率輸出的比較結果。

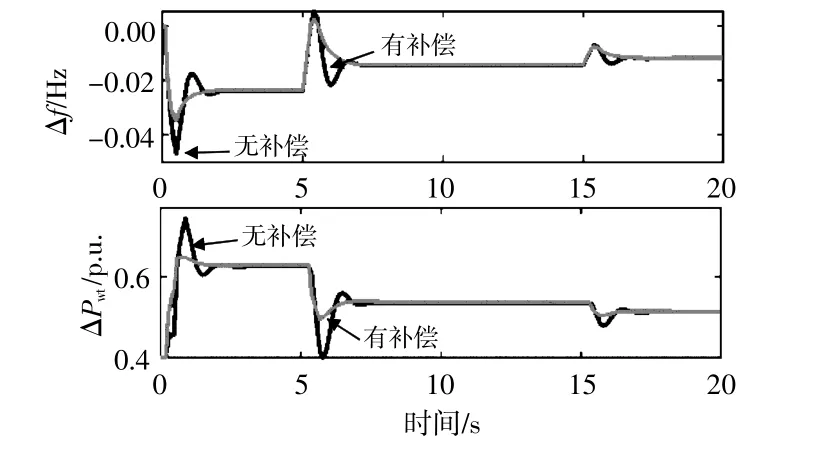
圖12 τ=0.4 s有無預測補償的系統動態響應對比圖Fig.12 Comparison diagram of system dynamic response with or without predictive compensation at τ=0.4 s

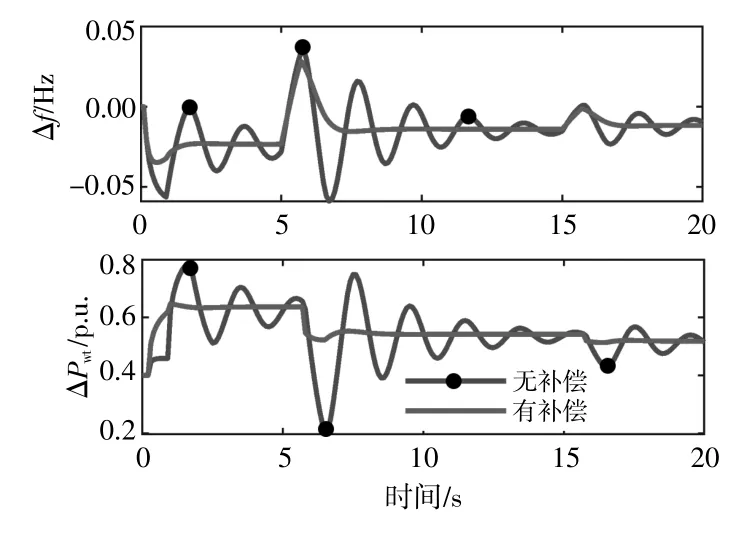
圖13 τ=0.8 s有無預測補償的系統動態響應對比Fig.13 Comparison diagram of system dynamic response with or without predictive compensation at τ=0.8 s

由圖12，13可知，在不采用延遲補償策略的情況下，變風速影響下風電擾動的動態響應過程會導致輸出的明顯振蕩。即使面對更接近實際的變風速來模擬通信延時，采用延遲補償方法也可以在較短的調節時間內有效地減少頻率振蕩量，更加快速穩定的跟蹤出力，保持系統頻率穩定。

5 結論

本文提出了一種基于模型預測控制的風電機組參與頻率響應的控制策略，基于傳統慣性調頻控制的理論，在傳統綜合慣性控制中引入了MPC算法，實現對慣性控制參數的實時更新，進而提高DFIG的慣性響應能力。本文所提方法能更好地協調儲能設備和常規機組的調頻出力，在通信延時工況和變風速擾動工況下調頻誤差較小，調頻效果較好，能夠盡量減小電網最大頻率偏差、穩態頻率偏移，減輕二次調頻壓力。提高了風電調頻對通信延時的魯棒性，為實際風電機組集群參與調頻設計控制策略提供參考。