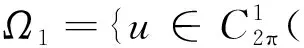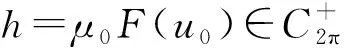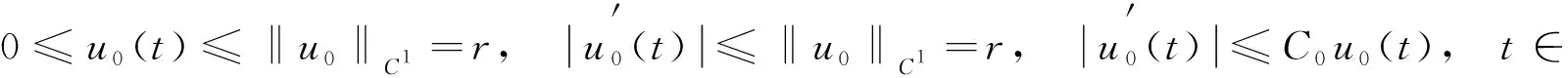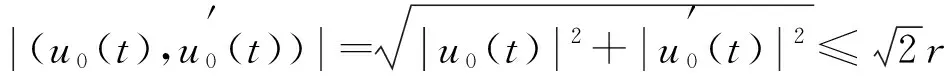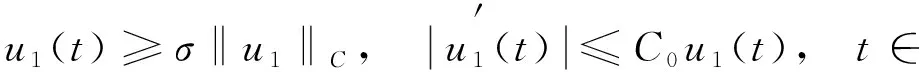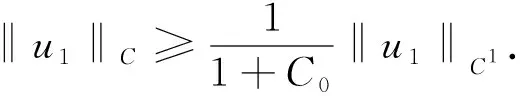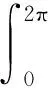具有非線性導數項的二階常微分方程的正周期解
劉曉明,李永祥
(西北師范大學 數學與統計學院,蘭州 730070)
-u″(t)+a(t)u(t)=f(t,u(t),u′(t)), t∈
正2π-周期解的存在性,其中: a: →(0,+∞)連續,以2π為周期;f: ×[0,+∞)×→[0,+∞)連續,f(t,x,y)關于t以2π為周期.在非線性項f(t,x,y)滿足適當的不等式條件下,得到了該方程正2π-周期解的存在性.
0 引 言
目前,關于二階常微分方程周期解的存在性研究已有很多結果,但已有工作主要集中在非線性項中不含未知函數導數的方程上,而對含未知函數導數的一般情形研究較少[1-5].本文研究非線性項中含未知函數導數的變系數二階常微分方程
-u″(t)+a(t)u(t)=f(t,u(t),u′(t)),t∈
(1)
正2π-周期解的存在性問題,其中系數函數a與非線性項f分別滿足下列條件:
(H1)a:→(0,+∞)連續,以2π為周期;
(H2)f:×[0,+∞)×→[0,+∞)連續,f(t,x,y) 關于t以2π為周期.
文獻[6-10]研究了該問題的一些特殊情形.文獻[6]討論了a(t)恒為常數M及f不含導數項u′(t)的情形:
-u″(t)+Mu(t)=f(t,u(t)),
(2)
在f(t,x)關于x超線性或次線性增長的條件下,用錐映射的Krasnoselskii不動點定理,獲得了方程(2)正2π-周期解的存在性.文獻[7]用正算子擾動方法與錐映射的Krasnoselskii不動點定理獲得了變系數二階微分方程
-u″(t)+a(t)u(t)=f(t,u(t))
(3)
正周期解的存在性與多重性結果.文獻[8]和文獻[9]用錐上的不動點指數理論分別對方程(2)和(3)建立了正周期解存在的特征值準則,即當f(t,x)連續,滿足下列條件之一時方程有正周期解:
(i)f0<λ1,f∞>λ1;
(ii)f0>λ1,f∞<λ1.
其中

(4)
而λ1為相應的線性周期特征值問題的最小正實特征值.對方程(2),λ1=M.文獻[8]和文獻[9]的特征值準則分別包含并改進了文獻[6]和文獻[7]的結果.此外,文獻[11-14]討論了二階微分方程
u″(t)+a(t)u(t)=f(t,u(t))
(5)
正周期解的存在性.與方程(3)不同,討論方程(5)的正周期解要求系數函數a(t)的值適當小,如文獻[13]要求:a(t)≤1/4,t∈[0,2π].此時,方程(5)的周期問題對應的Green函數是非負的,其正周期解可化為錐映射的不動點,從而可用與文獻[6-9]類似的方法獲得方程(5)的正周期解.

1 預備知識
設C2π()是以2π為周期的全體連續函數按最大模范數構成的Banach空間.一般地,對n∈,()表示以2π為周期的全體n階連續可微函數按范數
為討論非線性方程(1)正2π-周期解的存在性,先考慮相應的線性方程
-u″(t)+a(t)u(t)=h(t),t∈
(6)
2π-周期解的存在唯一性,其中h∈C2π().下面總假設a(t)滿足(H1).令

(7)
則0 -u″(t)+Mu(t)=h(t),t∈. (8) 由文獻[9]中引理2.1知,對?h∈C2π(),方程(8)存在唯一2π-周期解 (9) 其中 (10) 由式(9)直接驗證易知,方程(8)的周期解算子T:C2π()()是線性有界算子.記 取正常數 (11) 引理1線性方程(8)的周期解算子T作為C2π()到C2π()的線性有界算子,其范數且當()時,線性方程(8)的2π-周期解u=Th滿足估計: u(t)≥σ0‖u‖C, |u′(t)|≤C0|u(t)|,t∈. (12) 證明: 對?h∈C2π(),由式(9)及式(10),有 (13) 即式(12)的第一個估計式成立.另一方面,由式(9)得 從而由式(13)可得 即式(12)的第二個估計式成立.證畢. 下面考慮變系數線性二階微分方程(6)的2π-周期解的存在性. 引理2對?h∈C2π(),線性方程(6)存在唯一的2π-周期解(),且周期解算子S:C2π()()是線性有界算子.當()時,線性方程(6)的2π-周期解u=Sh是非負的,且滿足式(12). 證明: 改寫方程(6)為如下形式: -u″(t)+Mu(t)=Bu(t)+h(t),t∈, (14) 其中B:C2π()→C2π()為乘積算子 Bu(t)=(M-a(t))u(t),t∈. (15) 易見,B:C2π()→C2π()為正的線性有界算子,其范數‖B‖=M-m.按算子T:C2π()→C2π()的定義,方程(14)的2π-周期解等價于Banach空間C2π()中的算子方程 (I-TB)u=Th (16) 的解,其中I是C2π()中的單位算子.因為故由單位算子擾動定理,I-TB在C2π()中有有界逆算子,且其逆可展開為冪級數: (17) 故方程(16)(等價地方程(6))有唯一的2π-周期解 u=(I-TB)-1Th=∶Sh. (18) 由式(17),S=(I-TB)-1T可展開為 (19) 其中, (20) 為C2π()中的正線性有界算子.由T:C2π()()的有界性,S=TQ為C2π()到()中線性有界算子. u=Sh=T(Qh)=Th1, (21) 其中h1=Qh.由式(20),Q:C2π()→C2π()為正線性算子,故().因此,由引理1知,u=Th1滿足估計式(12). 下面考慮方程(6)相應的周期線性特征值問題: -u″(t)+a(t)u(t)=λu(t),t∈,(). (22) (23) 證明: 定義微分算子L:D(L)?C2π()→C2π()為 (24) 則特征值問題(22)可化為算子L的特征值問題 Lu=λu,u∈D(L). (25) 由引理2,L有有界逆算子L-1=S.因為S:C2π()()有界,故由嵌入()C2π()的緊性及引理2知,S:C2π()→C2π()是正的線性全連續算子.取h0(t)恒為1,則由引理2知,u=Sh0滿足估計式(12),從而有 Sh0≥‖Sh0‖Ch0. (26) 將式(26)兩端用S累次作用,并由S的正性可得 Snh0≥‖Sh0‖Cnh0,n=1,2,…, 因此有 由Gelfand譜半徑公式知,S的譜半徑為 (27) 由式(19)及式(9),有 因此λ1≥m,于是λ1∈[m,M]. (28) F(u)(t)∶=f(t,u(t),u′(t)),t∈, (29) Au∶=S(F(u)),u∈K. (30) 由S:C2π()()的有界性及嵌入()()的緊性知,S:C2π()()全連續.因此,由式(30)定義的A:K→K全連續.再由算子S的定義,方程(1)的正2π-周期解等價于A的非零不動點.下面用錐上的不動點指數理論[16]尋找A的非零不動點. 下面討論非線性方程(1)正2π-周期解的存在性.設σ0和C0是式(11)定義的正常數,λ1是線性特征值問題(22)的最小正實特征值. 定理1假設條件(H1),(H2)成立.若f:×[0,+∞)×→[0,+∞)還滿足下列條件: 1) 存在常數a,b≥0滿足a+C0b<λ1及常數δ>0,使得 f(t,x,y)≤ax+b|y|,x≥0,y∈, |(x,y)|≤δ; 2) 存在常數c>λ1及常數H>0,使得 f(t,x,y)≥cx,x≥0,y∈, |(x,y)|≥H. 則方程(1)至少有一個正2π-周期解. (31) μAu≠u,μ∈(0,1],u∈K∩?Ω1. (32) (33) 因為u0∈K∩?Ω1,由K和Ω1的定義,有 (34) 將方程(33)兩端同乘φ1(t),然后從0到2π積分,并應用不等式(34),得 對式(35)左端應用分部積分和式(23),有 從而由式(35),得 (36) 因為u0∈K,φ1=S(λ1φ1)∈K,由錐K的定義,有u0(t)≥σ0‖u0‖C,φ1(t)≥σ0‖φ1‖C,t∈.故有 于是由式(36)得λ1≤a+C0b,與條件1)中的假設矛盾.因此式(32)成立.從而由不動點指數理論的同倫不變性,有 i(A,K∩Ω1,K)=1. (37) 其次,令R>(1+C0)H/σ0.因為φ1=S(λ1φ1)∈K,故φ1∈K{θ}.下證A在K∩?Ω2上對e=φ1滿足缺方向性條件: u-Au≠τφ1,τ≥0,u∈K∩?Ω2. (38) 反設式(38)不成立,則存在τ1≥0及u1∈K∩?Ω2,使得u1-Au1=τ1φ1.因為 u1=Au1+τ1φ1=S(F(u1))+τ1S(λ1φ1)=S(F(u1)+τ1λ1φ1), (39) 又因為u1∈K∩?Ω2,由K和Ω2的定義,有 (40) (41) 于是,由式(40)的第一個不等式,有 (42) 將方程(39)兩端同乘φ1(t),再從0到2π積分,并對其左端應用分部積分,右端應用不等式(42),有 i(A,K∩Ω2,K)=0. (44) 從而由式(37)和式(44)及不動點指數的區域可加性,有 定理2假設條件(H1),(H2)成立.若f:×[0,+∞)×→[0,+∞)還滿足下列條件: 1) 存在常數c>λ1及δ>0,使得 f(t,x,y)≥cx,x≥0,y∈, |(x,y)|≤δ; 2) 存在常數a,b≥0滿足a+C0b<λ1及常數H>0,使得 f(t,x,y)≤ax+b|y|,x≥0,y∈, |(x,y)|≥H. 則方程(1)至少有一個正2π-周期解. i(A,K∩Ω1,K)=0. (45) 類似于式(37)的證明,當R適當大時,應用條件2)可證得 i(A,K∩Ω2,K)=1. (46) 于是由式(45),(46),有 注1在定理1中,條件1)與2)分別允許當|(x,y)|→0和|(x,y)|→∞時,非線性項f(t,x,y)關于x和y超線性增長,典型的例子是關于x和y的冪函數: (47) 其中α,β>0是常數.顯然,fα,β(t,x,y)滿足條件(H1).易驗證,當α,β>1時,f1(t,x,y)滿足定理1中條件1)知2).因此,條件1)和2)允許非線性項f(t,x,y)關于x和y任意階超線性增長. 注2在定理2中,條件1)和2)分別允許當|(x,y)|→0和|(x,y)|→∞時,非線性項f(t,x,y)關于x和y次線性增長,例如,當α,β∈(0,1)時,式(47)定義的冪函數fα,β(t,x,y),此時易驗證fα,β(t,x,y)滿足定理2中條件1)和2). 注3在定理1和定理2中,當f(t,x,y)不顯含y,退化為f(t,x)時,由式(4)易驗證: 定理1中條件1) ?f0<λ1, 定理1中條件2) ?f∞>λ1; 定理2中條件1) ?f0>λ1, 定理2中條件2) ?f∞<λ1. 因此,定理1的條件退化為(i),定理2的條件退化為(ii).此時定理1和定理2恰為文獻[9]中的特征值準則.故本文定理1和定理2概括并推廣了文獻[6-9]中的主要結果. 此外,本文定理1的不等式條件允許非線性項f(t,x,y)關于x和y任意階超線性增長,而已有的涉及超線性增長的工作,如關于周期問題的工作[3-4]和兩點邊值問題的工作[17-18],均要求f(t,x,y)關于y的增長滿足Nagumo條件.Nagumo條件限制了f(t,x,y)關于y至多二次增長,本文定理1突破了該限制.
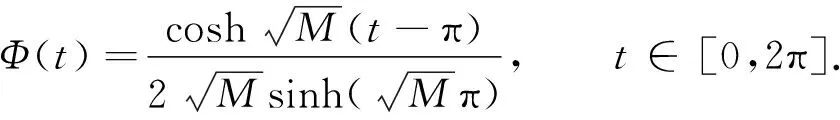
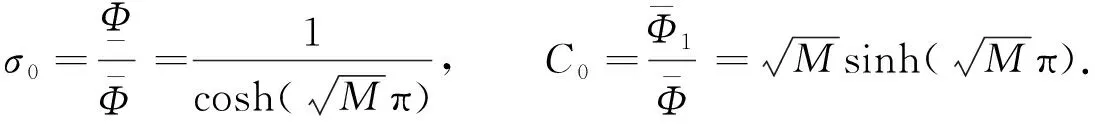
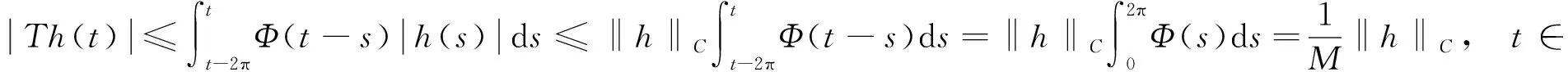

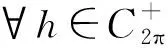






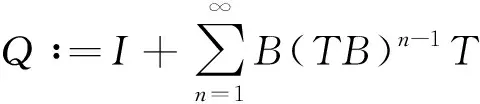


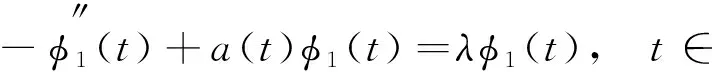






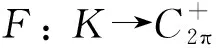
2 主要結果