分數階大氣混沌系統滑模同步的4個充分條件
毛北行,王東曉
(鄭州航空工業管理學院 數學學院,鄭州 450046)
1 引言與預備知識
目前混沌研究已取得較多的結果[1-5],由于大多數實際系統均需用分數階微分描述,且分數階系統大量存在于工程實際中,因此隨著分數階微積分的引入,分數階系統的滑模同步控制已引起人們廣泛關注[6-8],其研究結果在生物、化學、醫療衛生、通訊和物理等領域應用廣泛[9-12].滑模方法因其良好的魯棒性能,被迅速引入到混沌系統同步控制中[13-14],并在氣象學和天氣預測中應用廣泛.如文獻[15]研究了大氣混沌系統的系統仿真及動力學行為;文獻[16]研究了分數階大氣混沌系統的比例積分滑模同步;文獻[17]研究了分數階不確定大氣系統的自適應滑模同步,但設計的滑模面及控制量形式較復雜且不易實現.基于此,本文設計4種形式簡單的滑模面及控制輸入,得到分數階大氣混沌系統滑模同步的4個充分條件.
定義1[18-19]Caputo分數階微分定義為
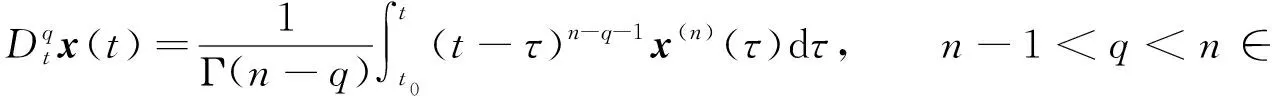
分數階大氣混沌系統[16-17]可描述為
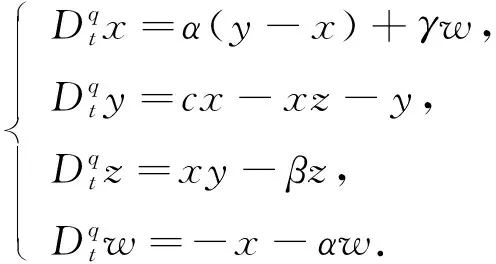
(1)
當α=1,β=0.7,γ=1.5,c=26,q=0.947時,系統(1)的吸引子和混沌吸引子分別如圖1和圖2所示.
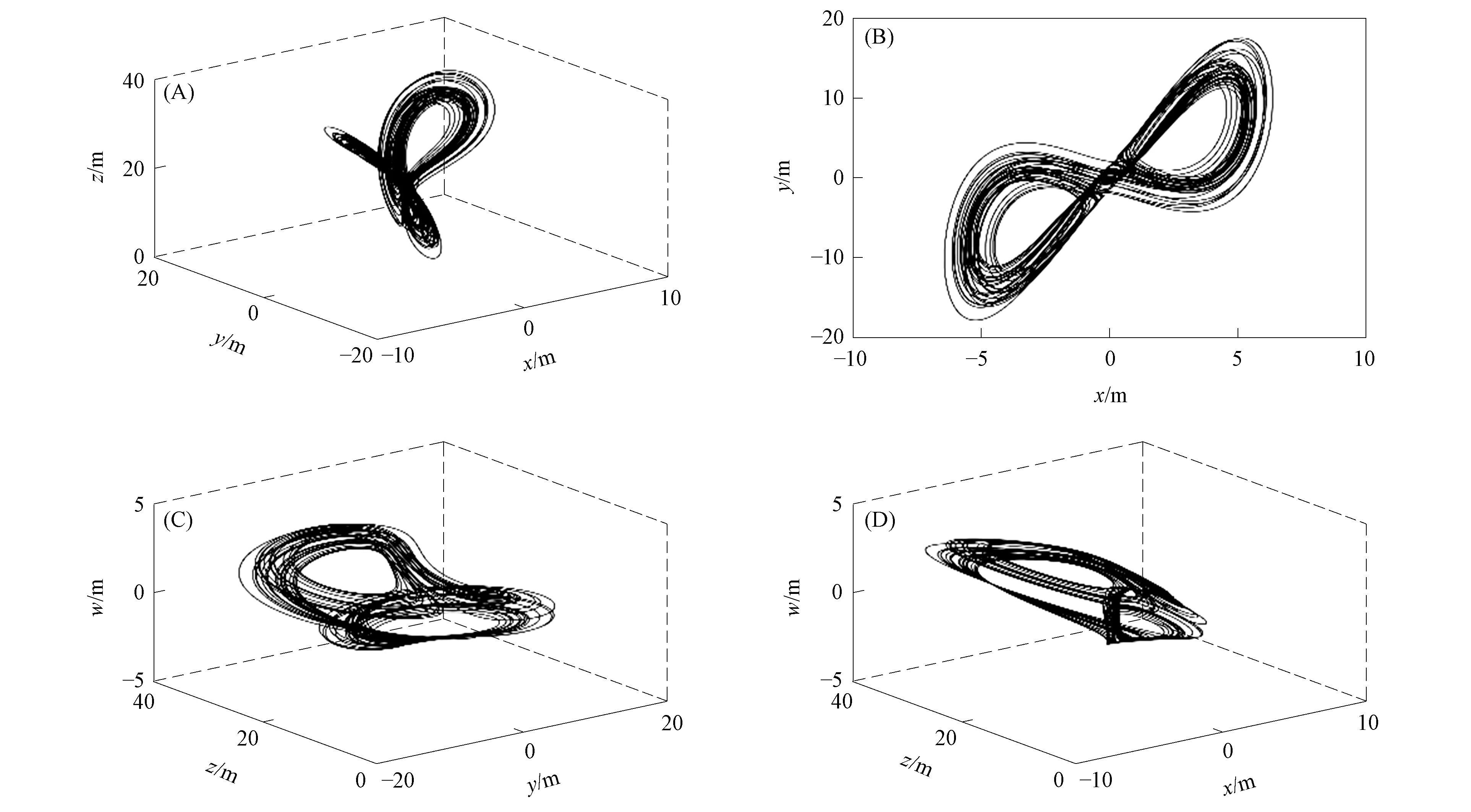
圖1 系統(1)的吸引子Fig.1 Attractors of system (1)

圖2 系統(1)的混沌吸引子Fig.2 Chaotic attractor of system (1)
定義從系統為
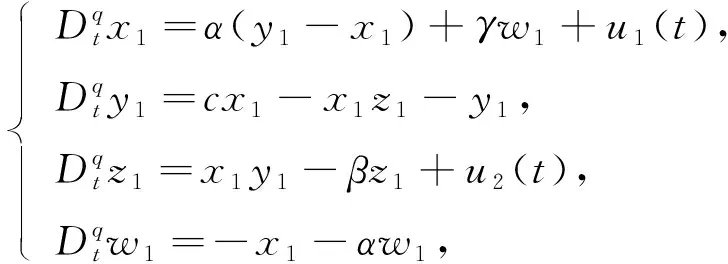
(2)
主從系統的同步誤差為
e1=x1-x,
e2=y1-y,
e3=z1-z,
e4=w1-w,
則有
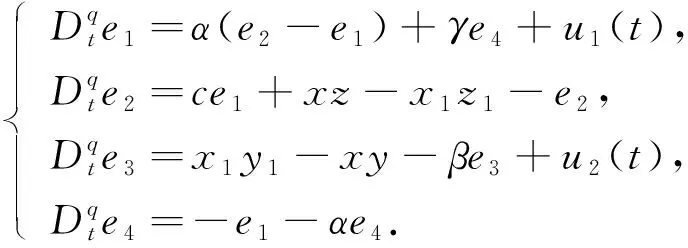
(3)
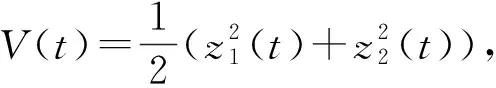
2 主要結果
定理1構造滑模面s(t)=e3+e1,控制量u1=-βe1-α(e2-e1)-γe4,u2=xy-x1y1,則系統(1)和系統(2)滑模同步.
證明: 當在滑模面上運動時,滿足s=0,即有e3=-e1.代入式(3)第3個方程可得e3→0,從而e1→0,代入式(3)第2個方程可得
xz-x1z1=(xz-x1z)+(x1z-x1z1)=-xe3-ze1→0,

從而得s(t)→0.
定理2構造滑模面s(t)=e4-e1,控制量u1=-(γ+1)e1-αe4-α(e2-e1),u2=xy-x1y1,則系統(1)和系統(2)滑模同步.

xz-x1z1=-xe3-ze1→0,

從而得s(t)→0.
以式(1)為主系統,設計從系統為

(4)
其中Δfi(y)為不確定項,y(t)=(x1,y1,z1,w1)T,di(t)為系統外部擾動,ui(t)為控制輸入,定義e1=x1-x,e2=y1-y,e3=z1-z,e4=w1-w,得到誤差系統
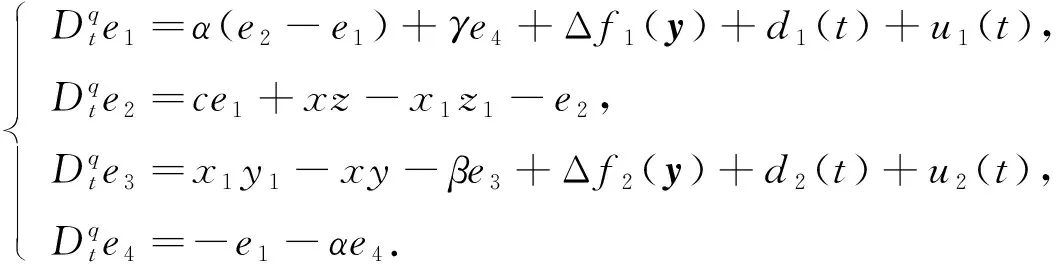
(5)
假設1|Δfi(y(t))|≤mi,|di(t)|≤ni(i=1,2),其中mi,ni>0為未知參數.
假設2|Δf2(y)+d2(t)|≤β|e3|.
定理3在假設1和假設2成立下,構造滑模面s(t)=e3+e1,控制量
若|s|>1,構造自適應律
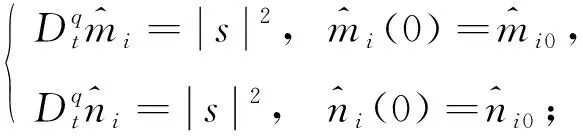
(6)
若0≤|s|≤1,構造自適應律
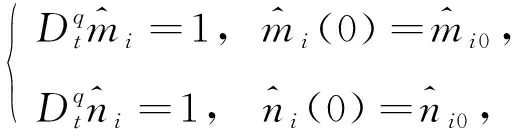
(7)

證明: 當在滑模面上運動時,滿足s=0,即有e3=-e1,代入式(5)第3個方程可得

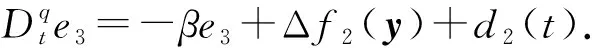
由假設2可得e3→0,即e1→0.代入式(5)第2個方程可得
xz-x1z1=(xz-x1z)+(x1z-x1z1)=-xe3-ze1→0,

當不在滑模面上運動時,若|s|>1,其自適應律為式(6),構造
求分數階導數可得
由引理2可得s(t)→0.
若0≤|s|≤1,其自適應律為式(7),構造
求分數階導數可得
由引理2可得s(t)→0.
定理4在假設1和假設2成立下,構造滑模面s(t)=e4-e1,控制量
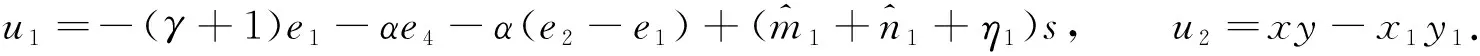
若|s|>1,構造自適應律
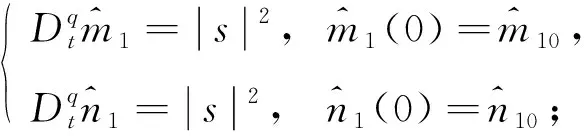
(8)
若0≤|s|≤1,構造自適應律
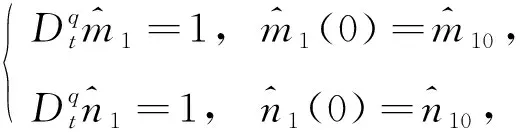
(9)


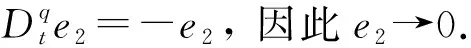
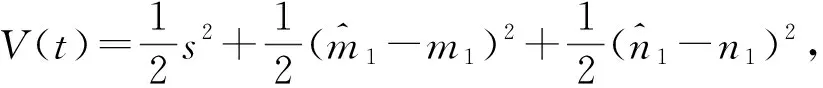
由引理2可得s(t)→0.

由引理2可得s(t)→0.
3 數值仿真

定理1~定理4的系統誤差曲線分別如圖3~圖6所示.由圖3~圖6可見,初始時的曲線誤差較大,但系統誤差最終趨近原點.定理1~定理4的控制量曲線分別如圖7~圖10所示,4個定理中均只需設計2個控制器,而一般的滑模方法均需設計4個控制器.由圖7~圖10可見,控制量隨系統誤差趨近于零而逐漸穩定在坐標原點附近,表明大氣混沌系統的驅動響應系統取得了滑模同步.在定理3和定理4中,針對滑模函數不同取值設計了不同的滑模自適應律,若不分區間設計滑模自適應律,則在仿真部分無法避免符號函數導致的抖振現象,分區間設計可較好避免這種現象,該問題的解決對了解和掌握大氣混沌運動規律及天氣氣象預報與海洋漁業捕撈均將發揮重要作用.
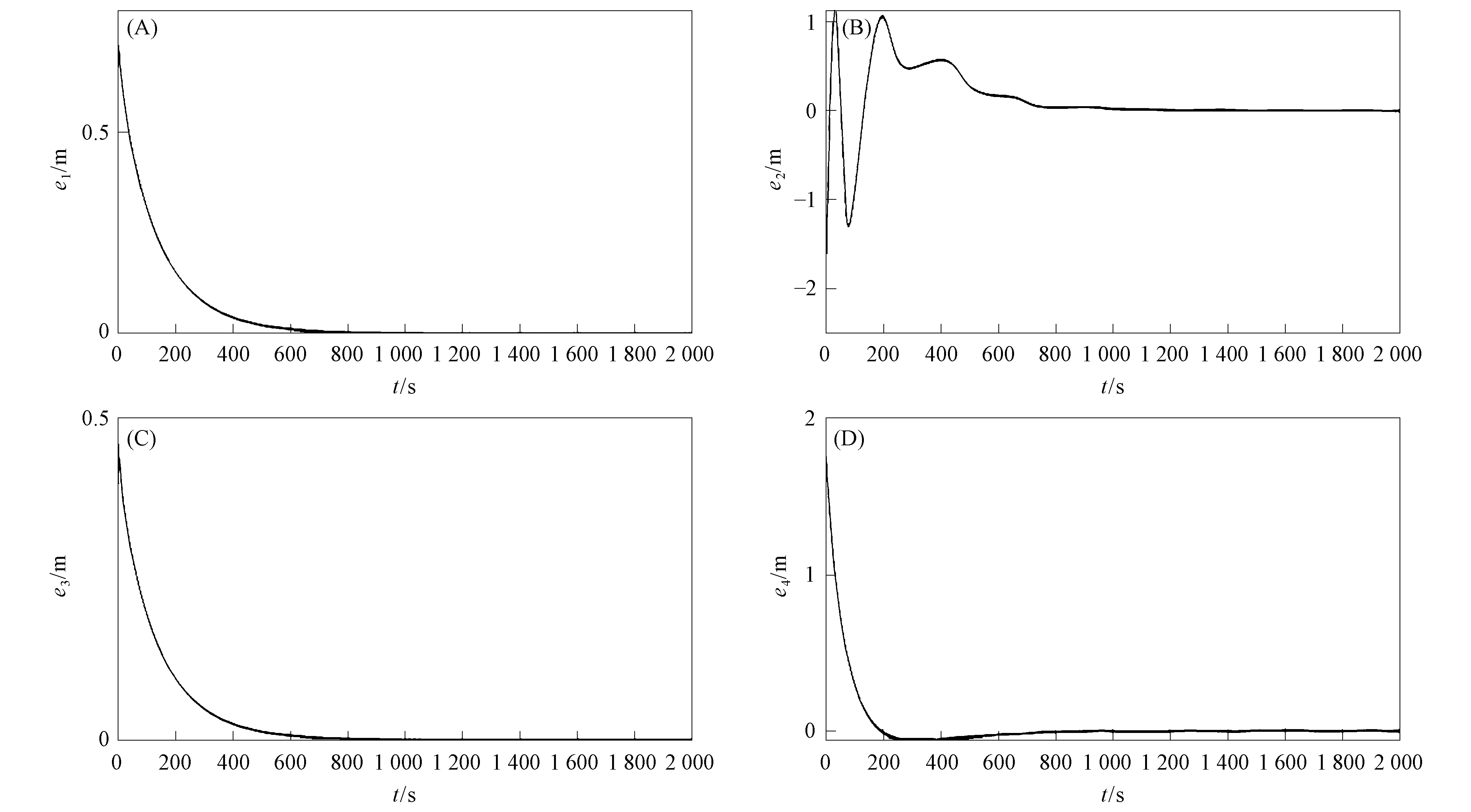
圖3 定理1的系統誤差曲線Fig.3 Systematic error curves of theorem 1
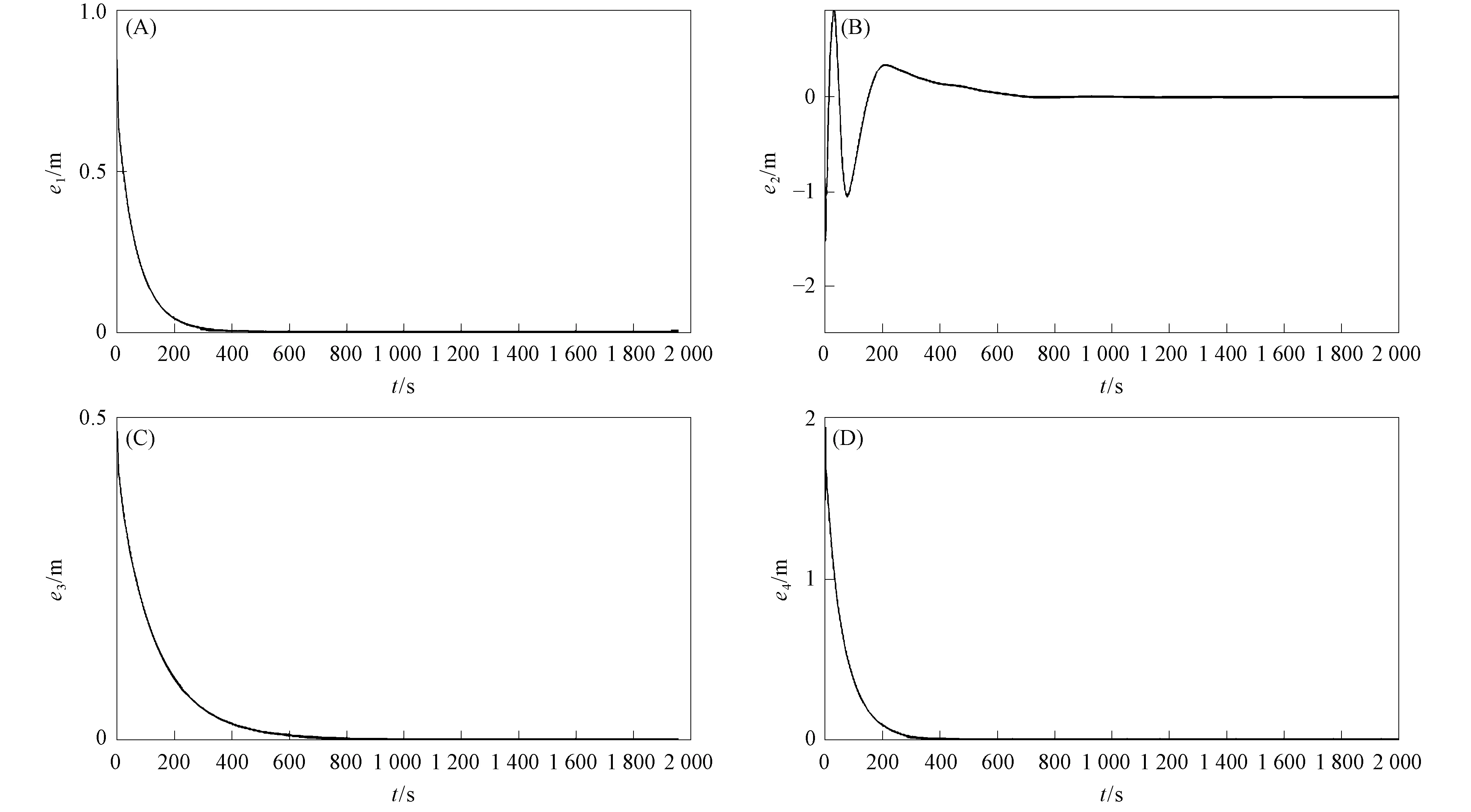
圖4 定理2的系統誤差曲線Fig.4 Systematic error curves of theorem 2

圖5 定理3的系統誤差曲線Fig.5 Systematic error curves of theorem 3
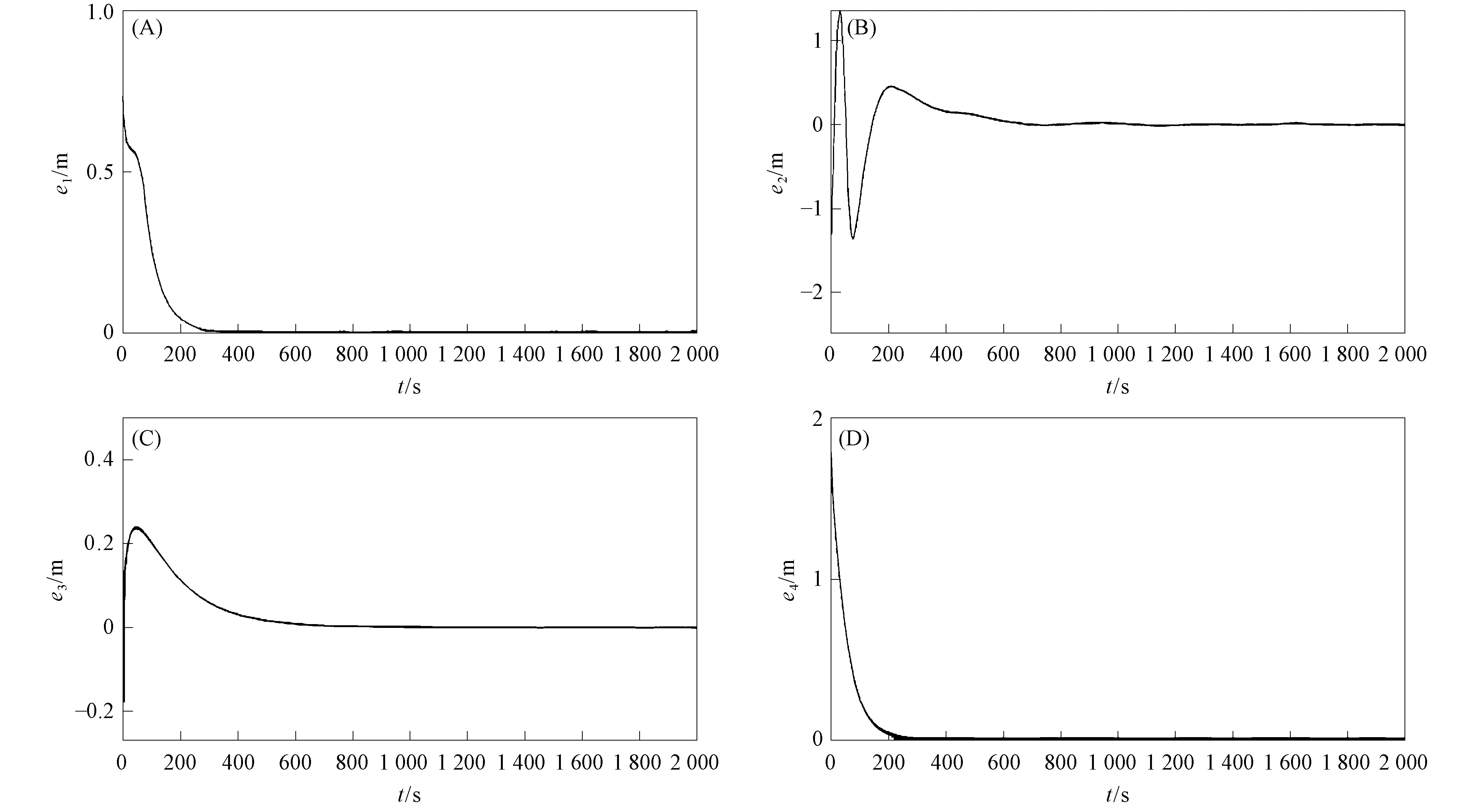
圖6 定理4的系統誤差曲線Fig.6 Systematic error curves of theorem 4
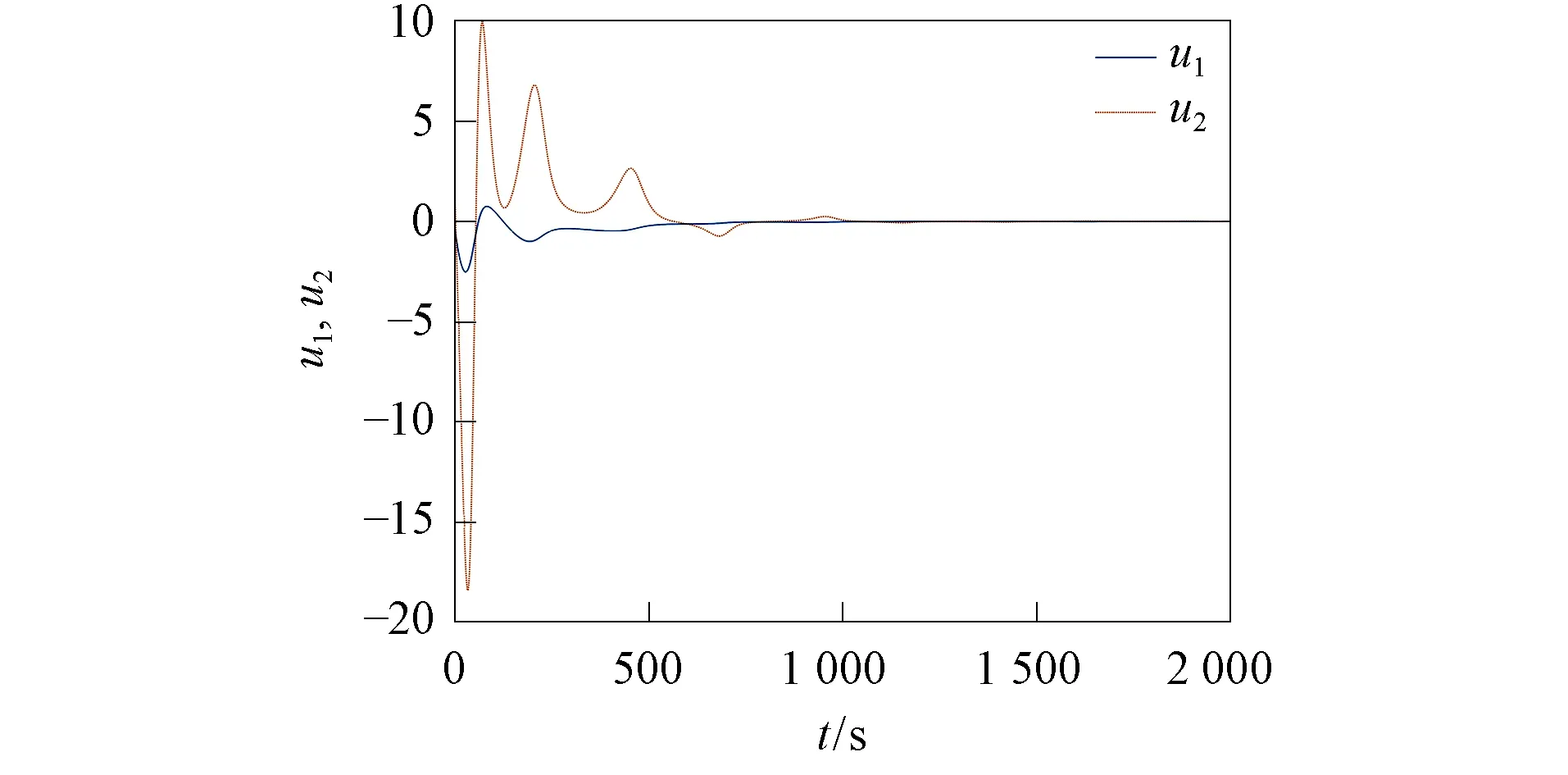
圖7 定理1的控制量曲線Fig.7 Control quantity curves of theorem 1
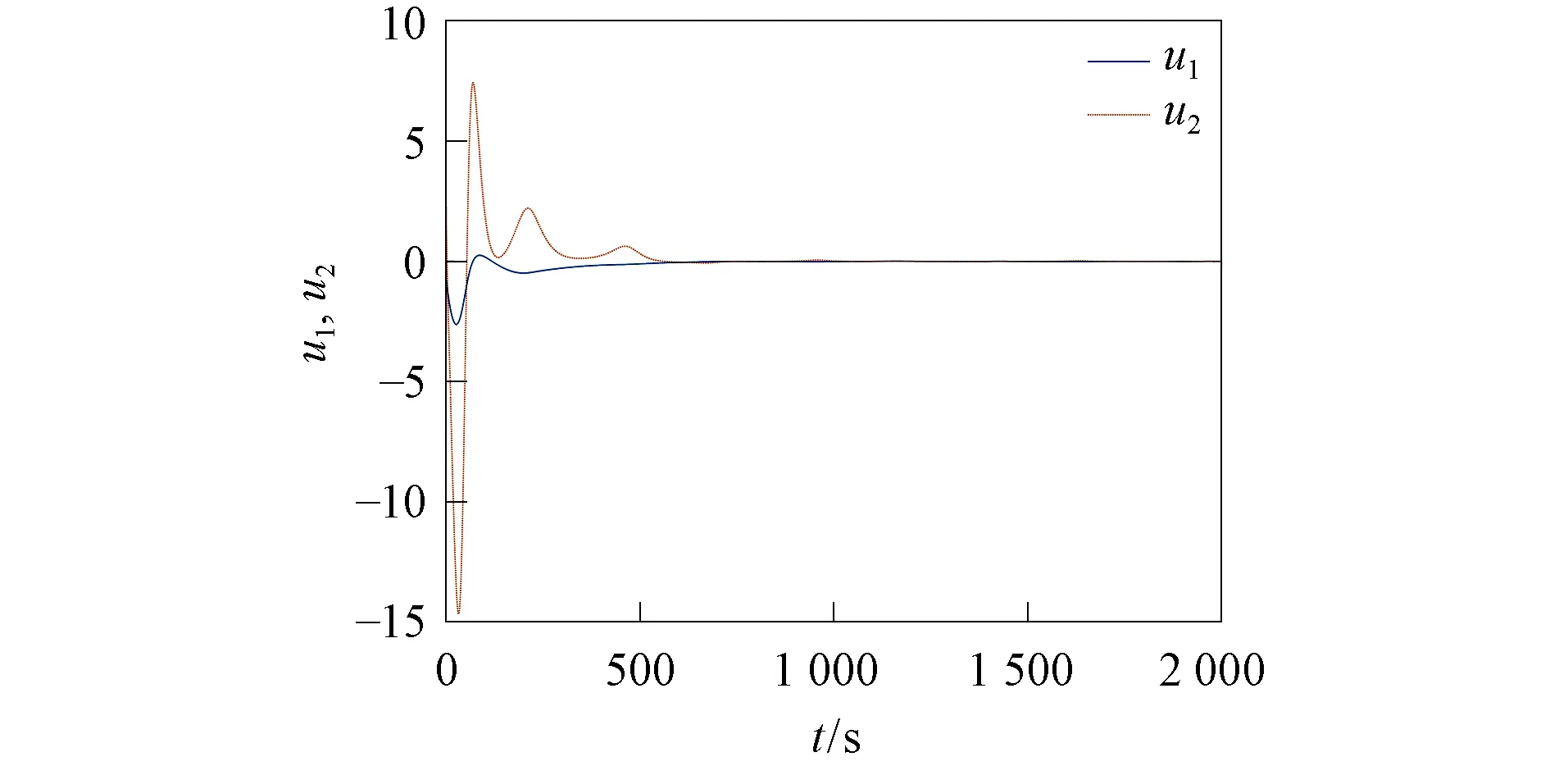
圖8 定理2的控制量曲線Fig.8 Control quantity curves of theorem 2

圖9 定理3的控制量曲線Fig.9 Control quantity curves of theorem 3

圖10 定理4的控制量曲線Fig.10 Control quantity curves of theorem 4
綜上,本文研究了分數階大氣混沌系統的滑模同步,通過引入分數階微積分將受控系統建模為分數階微分方程得到大氣混沌系統取得滑模同步的4個充分條件,并通過MATLAB仿真程序對結論進行驗證,結果表明,分數階大氣混沌系統在一定條件下主從系統可取得滑模同步.

