基于機器學習的三維數字圖像虛擬場景重建算法
宗 敏
(韓國清州大學 藝術學院,韓國 清州 28497;濰坊學院 傳媒學院,山東 濰坊 261061)
對圖像進行三維重構是目前計算機視覺領域研究的一個難點,其通過從實際圖像中得到準確的幾何信息[1],實現對圖像精準的虛擬還原.目前主要有兩種三維圖像重建技術: 1) 利用激光掃描儀、深度掃描儀等對空間目標進行三維立體測量;2) 將空間對象從影像中還原成立體結構,又稱為機器視覺[2-3].與第一種方法相比,基于圖像的三維重構技術更易獲取真實場景中的數據,隨著成像分辨率的提高,重構模型的精度也逐漸提升,應用領域更廣泛.霍林生等[4]提出了一種基于圖像壓縮算法的地震損傷三維模型快速重構方法,根據所得圖像重構出結構的三維數字模型;張豪等[5]提出了一種基于深度學習的重建方法,將所得的深度圖像轉化為三維模型,并通過三維對抗生成網絡,判定重建出的三維模型是否具有可信度,從而構建出真實的三維圖像模型.
雖然上述方法取得了一定進展,但構建的圖像精準度較低,細節部分不精細,因此本文提出一種基于機器學習的三維數字圖像虛擬場景重建算法.該算法的創新點是處理三維數字圖像,實現了紋理和角點的匹配,校正局部細節,利用分類器抑制離散特征點,提高重建效率,去除多余特征,分割點集得到近似擬合函數,分割三維曲面完成圖像重建.實驗結果表明,本文算法重建性能較好.
1 三維數字圖像虛擬場景渲染處理
在虛擬場景重建過程中,用場景的狀態和指示[6]對三維數字圖像進行繪制[7],將圖像的擴散角度設為10°,并以中間線為標準,表達式為
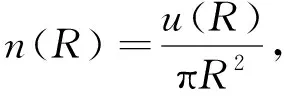
(1)
其中u(R)表示三維數字圖像中呈現數目,R表示圖像半徑.圖像的中心像素點分布基于gi=(gix,giy,giz)(i=0,1,2,…,Ng-1)特征空間模型,得到三維數字虛擬圖像重構網格模型G中第i個頂點的分布情況[8]:
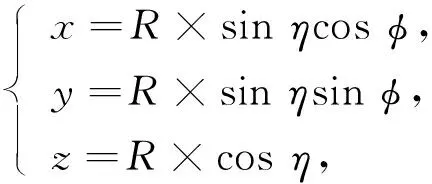
(2)
其中η表示三維數字虛擬圖像重構的網格變形因子,φ表示網格密度.從平面到中心線的縱向距離出發,得出初始樣本點與繪制幀之間的關系為
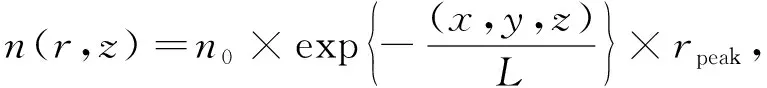
(3)
其中n0表示圖像表面積,rpeak表示圖像周長,L表示圖像高度[9].在三維虛擬場景中,給出相應的插值結果為
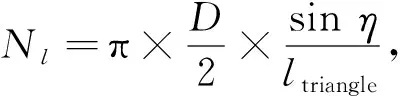
(4)
其中D表示插值系數,ltriangle表示相似度計算參數.
采用局部坐標法對圖像進行全局近似[10-11],獲得三維數字圖像的層次數,并對其進行紋理渲染和角點配準[12],校正局部細節,進行矢量反加權處理,得出三維數字圖像虛擬場景重建后的曲面像素特征分布,對三維數字圖像實行平滑操作[13],得到三維坐標系中的平滑算子為
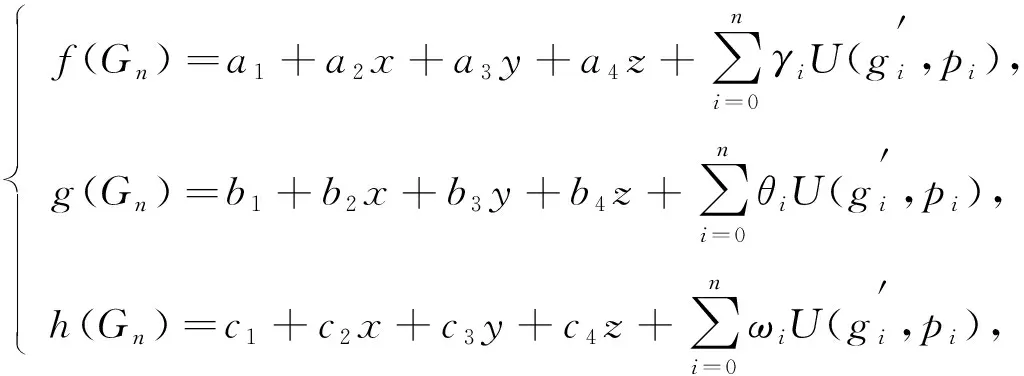
(5)
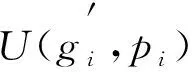
在此基礎上,完成三維數字圖像的渲染處理,根據所得效果抽取出相應的特征并匹配,從而完成三維數字圖像虛擬場景的繪制.
2 特征提取和匹配
為削弱在圖像角度提取中像素的變化程度,用下式降采樣建立符合規模的金字塔:
(6)
其中K(x,y,σ)表示圖像的標度空間,G(x,y,σ)表示高斯核函數[14],(x,y)表示像素坐標,I(x,y)表示輸入的二維圖像,σ表示比例空間系數.
在金字塔的各標度上進行Harris特征提取,以在空間和尺度上檢測到的極值點為特征點.根據響應函數在每一標度圖像上構建相應的窗口檢測模板[15],可表示為
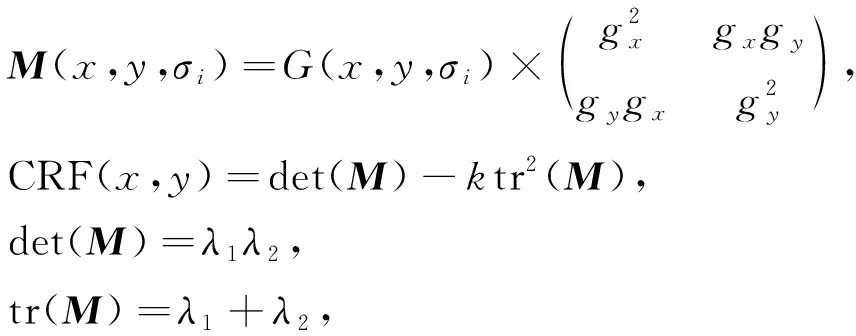
(7)
其中gx和gy分別表示沿x和y方向的圖像梯度[16],λ1,λ2表示矩陣M的兩個特征數,k表示不為零的常數.利用分類器對獲得的離散特征點實行極大抑制[17],以得到穩定的特征數值.
根據特征點的位置,畫出8×8的區域,并求出各像素點的梯度方向,表達式為
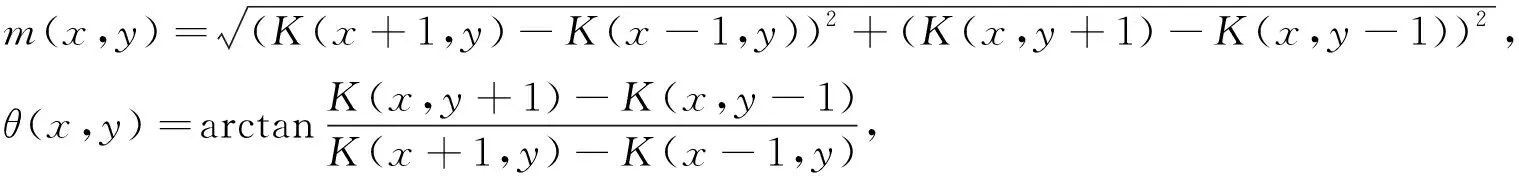
(8)
其中m(x,y)表示梯度模值[18],θ(x,y)表示梯度方向,K表示特征點的標度.用梯度直方圖的形式對區域內的梯度模值和方向進行統計,在0°~360°方向上,將各10°角的柱體分成8根,橫坐標表示直方圖的梯度方向,直方圖的高度表示梯度模值,如圖1所示.特征點主要方向是直方圖的峰值方向,在特征點的輔助方向上,僅保留峰值超過80%的方向,以提高匹配的魯棒性[19].
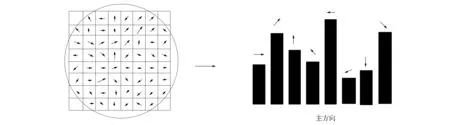
圖1 像素梯度和模值統計Fig.1 Pixel gradient and simulation statistics
利用特征點方向、尺度、坐標等信息,求出坐標軸方向,并在4×4的視窗內,通過對8個方向上的梯度信息進行處理,獲得128維向量的特征,即一個描述子.傳統尺度不變特征轉換(SIFI)方法計算很耗時,導致實時性差,因此本文將128維的特征矢量二值化,以f=(f1,f2,…,fi,…,f128)為特征矢量,定義二值化函數為
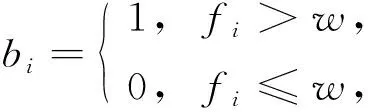
(9)
其中w表示臨界點.求f的中間值,將f矢量轉換成二進制矢量,可極大減少匹配運算的時間.
兩個特征點的匹配采用歐氏距離法,將待配點p,q的特征描述符用Desp,Desq表示,歐氏距離的計算公式為
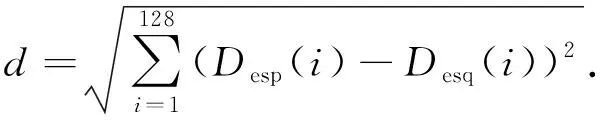
(10)
該方法通過使用有限k-d樹進行查找,以提高重建效率,最后利用隨機抽樣一致性算法去除不符合要求的特征點.基于上述過程對場景渲染處理,通過特征提取和匹配能對初始的視差進行校準,重建三維數字圖像虛擬場景.
3 三維數字圖像虛擬場景重建
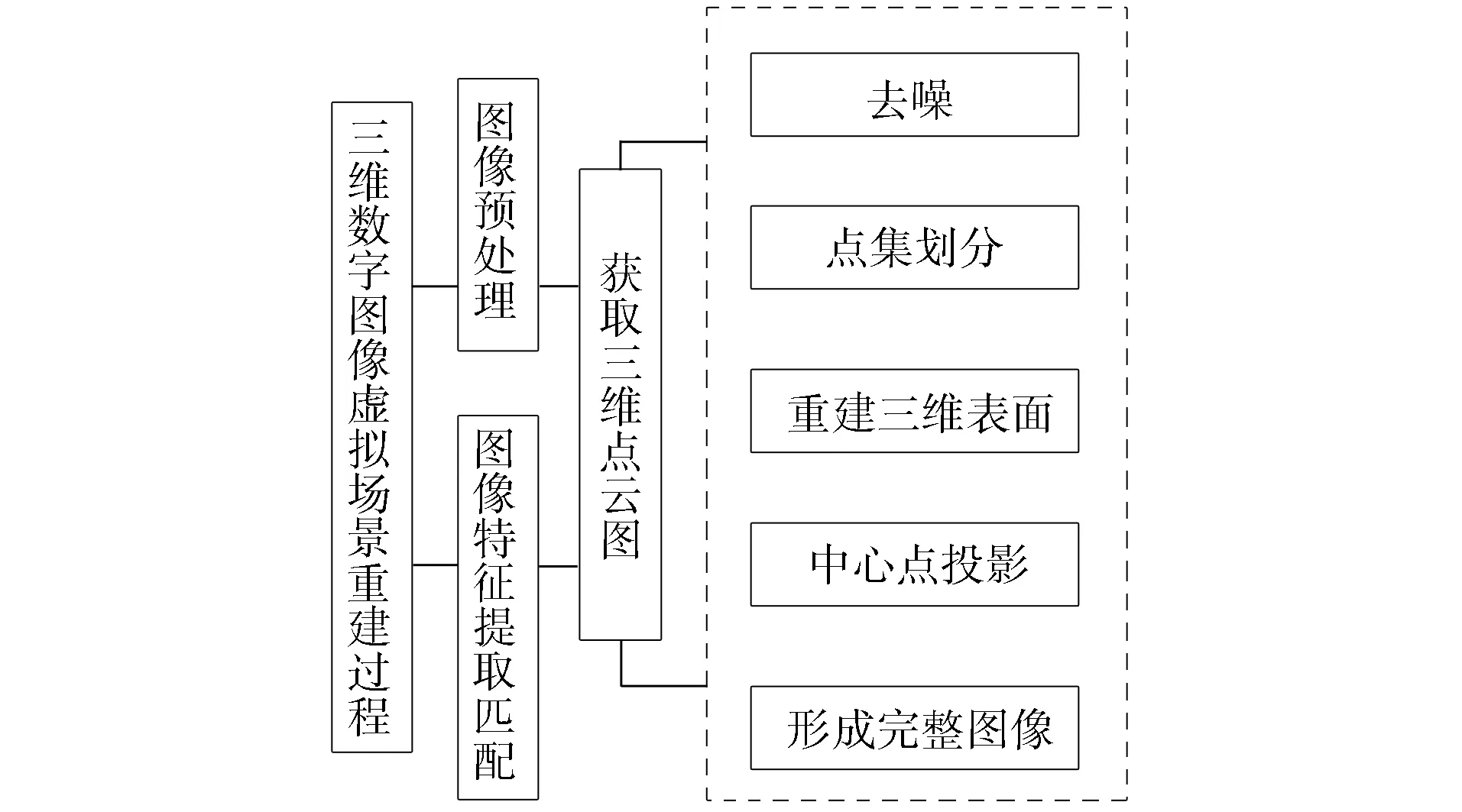
圖2 三維數字圖像重建過程Fig.2 Reconstruction process of 3D digital image
通過對場景渲染處理和特征提取,獲得三維數字空間特征點,得到場景目標表面的三維點云圖,構建出完整的三維數字圖像結構.圖2為三維數字圖像虛擬場景重建過程[20].最初三維點云的表面會出現突起點和凹點,導致重建表面不連續,出現漏洞,因此需要對三維點云進行優化,消除噪點,采用擬合函數法求出平滑后的三維坐標.
假設點集的整體擬合函數為χ,分割點集,則近似擬合坐標函數公式為
ηχ=δ(χ)×?s,
(11)
其中ηχ表示擬合函數,?s表示基函數數量,δ表示待分割的點集數目.根據式(11)的計算結果,采用最小二乘法重建三維曲面,以一個空間內的一個點為圓心,將該圓心投影到切面上,再用貪婪算法對該曲面進行局部二維三角分割,將其映射到三維空間內,構成一個完美的曲面,從而實現基于機器學習的三維數字圖像虛擬場景重建.
4 三維數字圖像重建實驗
為驗證本文算法的有效性,進行仿真實驗.以某三維數字圖像虛擬場景作為研究對象,實驗參數設置如下: 工作功率≤5 W,遙感圖像數量為100張,時間間隔為20 s,分辨率為200像素,圖像輸出為1 280像素×720像素和1 920像素×1 080像素,防護等級為一級.
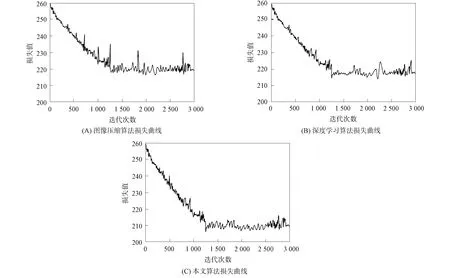
圖3 分類器驗證損失函數Fig.3 Loss function of classifier verification
分類器主要是對點云數據進行特征提取,即利用所抽取的特征矢量重建三維數字虛擬場景,得到點云數據.在分類訓練階段,每次訓練結束后,對驗證集進行校驗,得出校驗集合的損失曲線.圖3為3種不同算法的損失曲線.由圖3可見: 圖像壓縮算法得到的損失函數最小可達218;深度學習算法損失函數的最小值可達213;本文算法損失函數的最小值可達205.與其他兩種算法相比,本文算法得到的驗證集損失函數值較小.在固定橫坐標值下,當迭代次數為3 000時,3種算法的損失值分別為219,216和210.在固定縱坐標值下,當損失值降低至220時,其他兩種算法在1 000次迭代,本文算法在900次迭代.實驗結果表明,本文算法的收斂速度和效果均優于其他兩種對比算法.
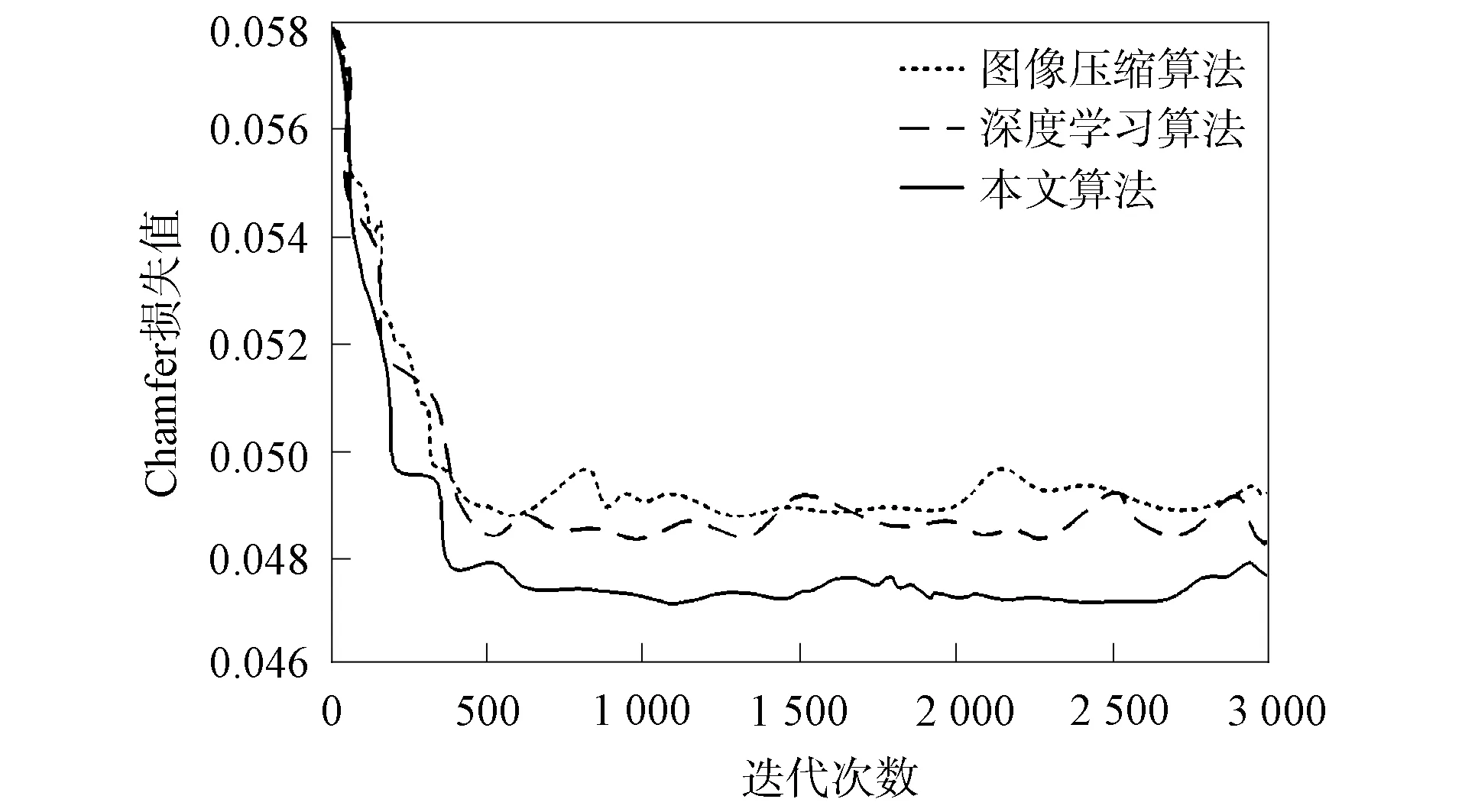
圖4 三維圖像重建網絡驗證集Chamfer距離對比Fig.4 Comparison of Chamfer distance of 3D image reconstruction network verification set
驗證集的Chamfer距離(倒角距離)表示每個點到最近特征點的距離,其數值越小證明重建圖像效果越好.圖4為三維圖像重建網絡驗證集Chamfer距離對比.由圖4可見: 圖像壓縮算法的損失函數隨著迭代次數的增加而下降,在第500次迭代時,降低到0.049;而深度學習算法比圖像壓縮算法的損失函數更低,表示三維重建效果較好;本文算法與其他兩種算法相比損失值最低,隨著迭代次數增加損失值達0.048以下,因此本文算法對三維圖像重建效果最佳,收斂性較快.
用一把椅子做實驗對象,能明顯看出不同算法對原始圖像中靠背和椅子腿的空洞部分的描述.將3種算法的實驗結果可視化,如圖5所示.圖5(A)為需要重建的圖像,以此作為圖像構建的基準.由圖5(B)可見,圖像壓縮算法重建的椅子圖像靠背處空洞和椅子腿部分沒有被很好地呈現,尤其是椅子腿位置已看不出任何形狀,視覺觀察只是各種點狀,重構圖像整體效果不佳.由圖5(C)可見,深度學習算法雖然整體椅子形狀顯示出來了,但明顯觀察到表面呈現一些冗余的紋理,與重建圖像有較大差異,但相對圖像壓縮算法總體效果較好.由圖5(D)可見,本文算法重建的圖像效果最佳,邊緣輪廓以及細節部分分布均勻,重構更精細,椅子表面平整,精準度比其他兩種算法都高.因此本文算法對三維數字圖像重建完整性更好,細節精度也較高,能呈現清晰紋理.
實驗結果表明,本文算法的收斂速度和效果優于其他兩種對比算法,得到的驗證集損失函數值較小;同時本文算法重建的圖像效果最佳,邊緣輪廓以及圖像細節部分分布均勻,重構更精細,完整性更好,能呈現出清晰紋理.
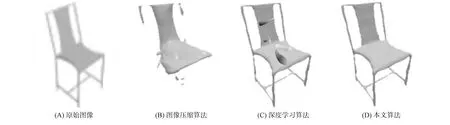
圖5 三維圖像重建可視化結果比較Fig.5 Comparison of 3D image reconstruction visualization results
綜上可見,針對傳統的三維重構技術主要采用三維模型,使得三維重建工作量較大,耗時較長,模型的構建效率較低,已無法滿足人們生產和生活需要的問題,本文提出了一種基于機器學習的三維數字圖像虛擬場景重建算法.首先,將三維數字圖像進行紋理渲染,角點配準,并對局部細節進行校正,獲得去除噪聲圖像;其次,采用分類器對離散特征點進行抑制,增強重建效率,剔除多余的特征,利用點集得到近似擬合函數;最后,對三維圖像表面分割,實現三維數字圖像虛擬場景重建.通過實驗可得如下結論:
1) 本文算法得到的驗證集損失函數值較小,在固定的縱坐標值中,當損失值降低至220時,其他兩種對比算法在1 000次迭代,本文算法在900次迭代,表明本文算法的收斂速度和效果均優于其他兩種算法.
2) 本文算法重建的圖像效果最佳,邊緣輪廓以及圖像細節部分分布均勻,對三維數字圖像重建有較好的完整性,細節精度較高,能呈現清晰紋理特征.

