基于檢測行為的動物布病模型的動力學分析

王燕飛,侯 強,胡紅萍

(中北大學 數學學院,太原 030051)

0 引 言

動物疫病的防控措施主要有免疫、消毒、檢測撲殺.目前,關于免疫對動物疫病傳播的影響[1-3]以及撲殺行為對動物疫病傳播的影響研究[4-6]已有一些成果.

關于檢測撲殺的研究,文獻[7]基于布病的傳播特征建立了動力學模型,其檢測信息主要來源于新發現的染病動物;文獻[8]以染病人數作為檢測信息建立了人畜耦合的布病傳播動力學模型,結果表明,檢測標準會產生周期震蕩;文獻[9]通過限制撲殺資源研究了檢測撲殺措施對布病傳播的影響;文獻[10]建立了布病傳播的時滯模型,反映了通過血清學檢測發現染病動物過程的特點,發現信息收集的遲滯會導致疾病傳播的周期震蕩.上述研究反映了布病傳播動力學的一些特征,但均未考慮具有臨床特征和檢測發現的染病動物未得到及時處理導致傳染這一風險因素.因此,基于上述分析,本文將具有臨床特征的染病動物作為檢測信息來源,建立動力學模型,分析檢測行為對動物布病傳播的影響.

本文將動物種群分為4類: 易感動物S(t),潛伏動物E(t),無臨床特征的染病動物I(t),具有臨床特征和檢測發現的染病動物Id(t).這里檢測出的染病動物是從無臨床特征的染病動物I(t)中發現的,在潛伏期染病的動物通過檢測很難發現,因此假設潛伏期動物不會通過檢測發現.種群動物總數用N(t)表示,則有

N(t)=S(t)+E(t)+I(t)+Id(t).

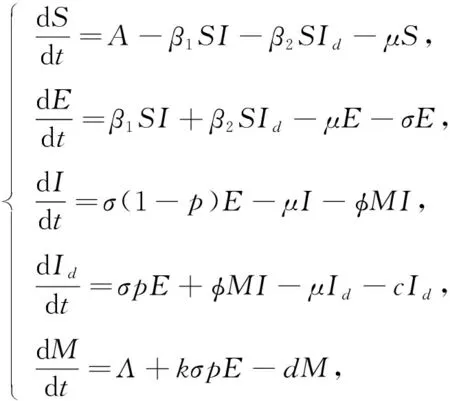
(1)

其中,A表示動物的常數輸入率,β1表示易感動物與無臨床特征染病動物之間接觸的傳染率,β2表示易感動物與具有臨床特征和檢測發現的染病動物之間接觸的傳染率,μ表示動物的自然死亡率,σ表示潛伏期動物的轉移率,p表示有臨床特征的動物比例,c表示被發現染病動物的捕殺率,Λ表示固定監測單位提供的信息量,k表示信息的增長率,d表示信息減少的比率.所有參數均為正.

1 平衡點和后向分支

1.1 無病平衡點

當動物布病不存在時,即I=Id=0,經簡單計算可知,模型(1)有無病平衡點

由下一代矩陣法[11]可知,

則模型(1)的基本再生數為

容易驗證,

為模型(1)的可行域.

1.2 地方病平衡點

經計算有

且E*滿足

f(E*)=BE*2+CE*+D=0,

(2)

其中

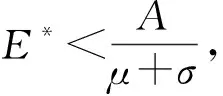
1) 當R0>1時,方程(2)有唯一的正根;

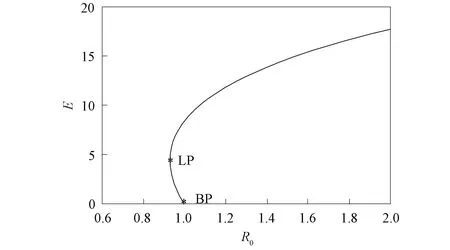
圖1 后向分支Fig.1 Backward bifurcation

2) 當R0<1,C<0時,方程(2)無正根;當R0<1,C>0時,若C2=4BD,則方程(2)有一個正根,若C2>4BD,則方程(2)有兩個正根.

綜上,可得:

定理11) 當R0>1時,模型(1)有唯一的地方病平衡點;

2) 當R0<1,C<0時,模型(1)沒有地方病平衡點;

當R0<1,C>0時,若C2=4BD,則模型(1)有一個地方病平衡點,若C2>4BD,則模型(1)有兩個地方病平衡點,如圖1所示.

1.3 后向分支

定理2當

時,模型(1)在R0=1處發生后向分支.

證明: 用中心流形方法[12]分析模型(1)后向分支的存在性.

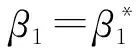
為簡化和理解中心流形定理,令

S=x1,E=x2,I=x3,Id=x4,M=x5,

則模型(1)變為

(3)

模型(3)在無病平衡點處的Jacobi矩陣為

當R0=1時,其特征方程為

h(λ)=λ(λ+μ)(λ+d)(λ2+a1λ+a2),

其中

模型(3)的特征方程有零特征值,且其他特征值為負.設與零特征值相關的右特征向量為ω=(ω1,ω2,ω3,ω4,ω5)T,其中

設與零特征值相關的左特征向量為v=(v1,v2,v3,v4,v5),其中

令a,b表示相關分支系數,則

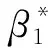
時,有a>0,因此模型在R0=1處發生后向分支,如圖1所示.

2 平衡點的穩定性

2.1 無病平衡點的局部穩定性

定理3當R0<1時,無病平衡點P0是局部漸近穩定的.

證明: 模型(1)在無病平衡點的Jacobi矩陣為

矩陣J0的特征多項式為

(λ+μ)(λ+d)(λI3-B1)=0,

(4)

其中

當R0<1時,有R1<1,R2<1.

矩陣-B1的所有一階主子式顯然為正;矩陣-B1的二階主子式為

矩陣-B1的三階主子式為

所以矩陣-B1的所有主子式為正,即-B1的特征值實部均大于0,則矩陣B1的特征值實部均小于0,于是式(4)中的特征值實部均小于0.因此,當R0<1時,無病平衡點P0是局部漸近穩定的.

2.2 無病平衡點的全局穩定性

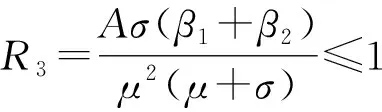
證明: 經計算有R3>R0.構造Lyapunov函數

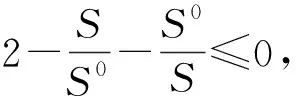
3 模型的一致持續性

定理5當R0>1時,模型(1)是一致持續的,即存在一個正數,使得

2.開展績效考核，可以使職工更加清楚自身具有的能力和優勢所在，還能發現自身存在的缺點和不足之處。在培訓后，并接受領導的指導，從而更好的提升自身能力和業績，獲得晉升機會和加薪機會，從而實現職工自己的個人價值和追求。

成立.

證明: 定義

X0={(S,E,I,Id,M)∈X:E>0,I>0,Id>0}, ?X0=XX0.

首先,X是正不變集,?X0是閉集.

設

M?={φ∈X:Φ(t)φ∈?X0,t≥0},Φ(t)φ=Φ(t,φ(t)),

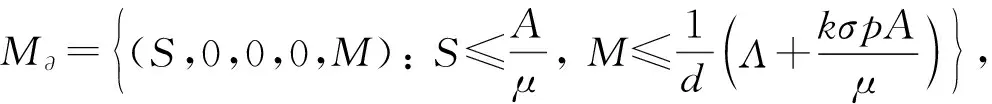
1) 存在t0≥0,使得E(t)>0,I(t)=0,Id(t)=0,則

2) 存在t0≥0,使得E(t)=0,I(t)>0,Id(t)=0,則

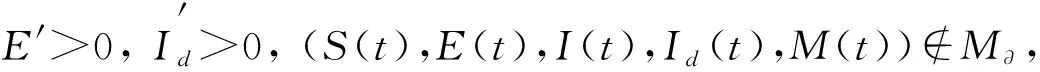
3) 存在t0≥0,使得E(t)=0,I(t)=0,Id(t)>0,則

E′=β2SId>0.

從而存在δ>0,使得當t0≤t≤t0+δ時,E′>0,(S(t),E(t),I(t),Id(t),M(t))?M?,矛盾.

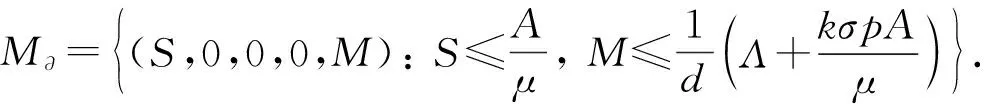
對任意足夠小的ε>0,有

(5)

下面證明對任意的φ∈X,存在ρ=ρ(ε)>0,使得

(6)

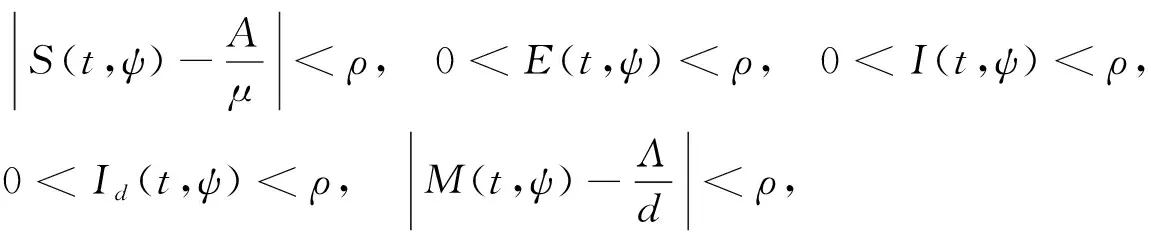
(7)

從而對任意的t>t0+T,式(5)成立.由模型(1)可得

考慮以下輔助模型:

(8)

模型(8)的Jacobi矩陣J為

J=J1-εG,

其中

4 最優控制策略

為盡可能降低染病動物的數量,制定一個最優的控制策略很重要.因此,在模型(1)中引入與時間相關的控制項μ1(t),μ2(t),增加控制后的模型為

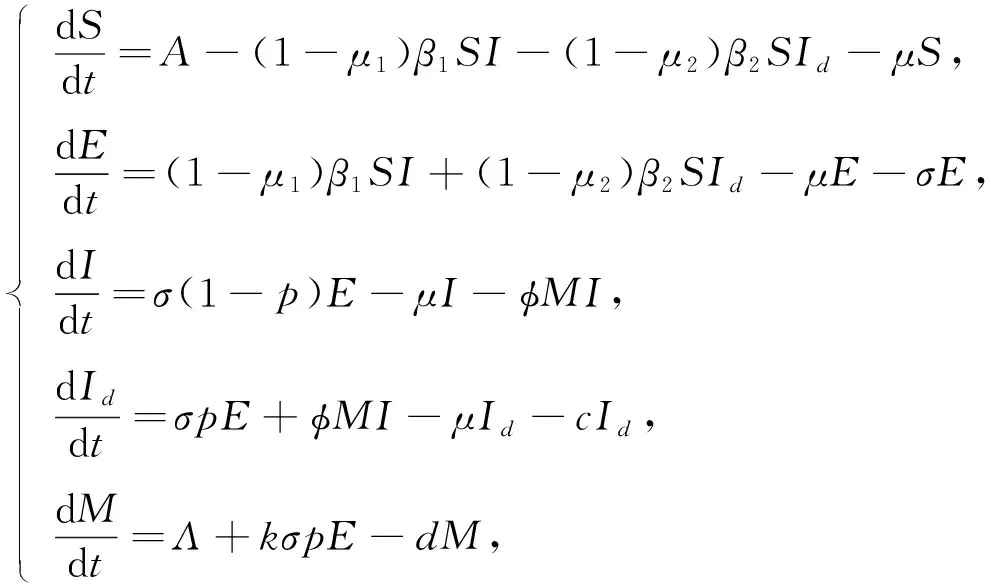
(9)

其中μ1(t)表示減小易感動物與無臨床特征的染病動物接觸的隔離策略,μ2(t)表示減小易感動物與有臨床特征和檢測發現的染病動物接觸的隔離策略.控制函數集為

U={U(·)∈L′([0,T];2)|0<μi≤μmax<1,?t∈[0,T]}.

目標是降低染病動物的數量,定義目標函數為

其中μ=(μ1(t),μ2(t)),P1為無臨床特征染病動物的權重系數,P2為有臨床特征和檢測發現的染病動物的權重系數,C1,C2為控制策略的權重系數.

根據Pontryagin Maximum原理[16],定義Hamilton函數為

其中λi(i=1,2,…,5)是伴隨變量.各伴隨變量的微分方程為

從而有

并且滿足橫截條件λi(T)=0(i=1,2,…,5).

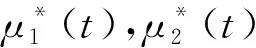
可知,最優控制解為

5 數值模擬

A=9,β1=0.01,β2=0.2,μ=0.2,σ=0.01,

p=0.2,φ=0.06,c=0.08,Λ=0.02,k=2,d=0.01,

此時R0=0.82<1,最優控制曲線如圖2所示.取參數

A=12,β1=0.3,β2=0.5,μ=0.8,σ=0.4,

p=0.3,φ=0.12,c=0.2,Λ=8,k=0.6,d=0.1,

此時R0=2.47>1,最優控制曲線如圖3所示.無論R0<1還是R0>1,采取最優控制方法后,染病動物的數量在短時間內可快速減少,因此最優策略的應用可有效控制動物布病的傳播.

綜上所述,為研究檢測行為對動物布病傳播的影響,本文首先將具有臨床特征的染病動物作為檢測信息,建立了動力學模型.其次,利用定性和穩定性理論,分析了模型平衡點的存在性和穩定性,并證明了模型后向分支的存在性.結果表明: 當模型發生后向分支時,即使R0<1,動物布病仍可能持續存在;當R0>1時,模型有唯一平衡點且模型一致持續.最后,通過數值模擬說明了控制策略可使染病動物的數量在短時間內快速減少,從而有效阻止動物布病的傳播.因此,在對動物進行檢測撲殺時,結合最優控制策略,更有利于動物布病風險管理措施的制定.