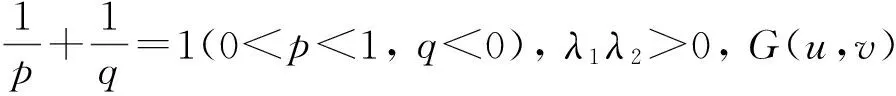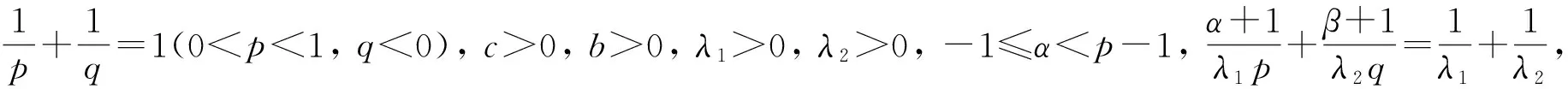廣義齊次核半離散Hilbert型逆向不等式的構造定理及算子表示
洪 勇,趙 茜
(1.廣州華商學院 應用數學系,廣州 511300;2.廣東財經大學 統計與數學學院,廣州 510320)
1 引言與預備知識
設r≠0,α∈,


(1)
稱為半離散Hilbert型逆向不等式,M稱為常數因子.
Hilbert型不等式對于研究加權賦范序列空間和加權Lebesgue空間的算子問題有重要作用,目前已取得了許多研究成果[1-14],但對Hilbert型逆向不等式的研究文獻報道較少[15-17],特別是對其構造條件的探討不多,本文在文獻[18]討論Hilbert型積分不等式構造條件的基礎上,討論半離散Hilbert型逆向不等式的構造條件和最佳常數因子的計算問題.
設G(u,v)是λ階齊次非負函數,K(n,x)=G(nλ1,xλ2)稱為廣義齊次核,K(n,x)具有如下性質: 若t>0,則
K(tn,x)=tλλ1K(n,t-λ1/λ2x),K(n,tx)=tλλ2K(t-λ2/λ1n,x).
特別地,有K(t,1)=tλλ1K(1,t-λ1/λ2),K(1,t)=tλλ2K(t-λ2/λ1,1).
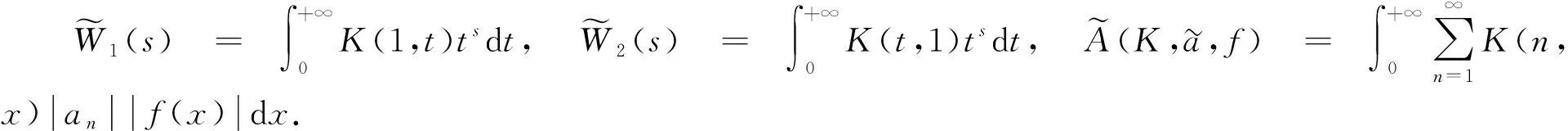
引理1設1/p+1/q=1(0

證明: 根據廣義齊次核K(n,x)的性質,有
又因為K(t,1)t-(α+1)/p在(0,+∞)上遞減,故有

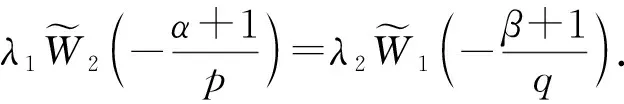
引理2設1/p+1/q=1(0 當且僅當an=C1(常數)和f(x)=C2(常數)時,式(2)取等號. 證明: 因為1/p+1/q=1(0 (3) 當且僅當an=C1(常數)時,式(3)取等號. 又根據積分型H?lder逆向不等式和式(3),有 根據式(3)和式(4)取等號的條件可知,當且僅當an=C1和f(x)=C2時,式(2)取等號. (5) 從而有 因為K(t,1)t-(α+1)/p在(0,+∞)上遞減,故有 于是可得 (6) 令 從而可視ε為一個趨于0的正項數列{ck},利用Lebesgue控制收斂定理,得 進而在式(6)中令ε→0+,得 (7) 矛盾.故cλ2>0不成立. 若cλ2<0,則對充分小的ε>0,取an=n(-α-1-|λ1|ε)/p(n=1,2…), 從而有 并有 從而可得 令ε→0+,同理可得矛盾的式(7),因而cλ2<0也不成立. 設K(n,x)≥0,定義以K(n,x)為核的離散算子T1和積分算子T2分別為 (8) 于是由定理1,可得如下等價結果. (9) (10) 在定理2中取α=β=0,可得如下推論. (11) ‖T2(f)‖q≥M‖f‖q,f(x)∈Lq(0,+∞); (12) 在定理2中取λ1=λ2=1,可得齊次核算子的如下推論. (13) 則 證明: 令G(u,v)=exp{-c(u/v)b},則G(u,v)是λ=0階齊次非負函數, 又記K(n,x)=G(nλ1,xλ2)=exp{-c(nλ1/xλ2)b},因為c>0,b>0,λ1>0,α≥-1,故K(t,1)t-(α+1)/p=exp{-ctλ1b}t-(α+1)/p在(0,+∞)上遞減. 同理,可得 綜上并根據定理2知推論3成立.證畢.
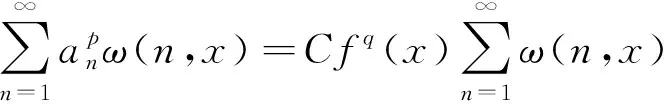
2 半離散Hilbert型逆向不等式的構造定理

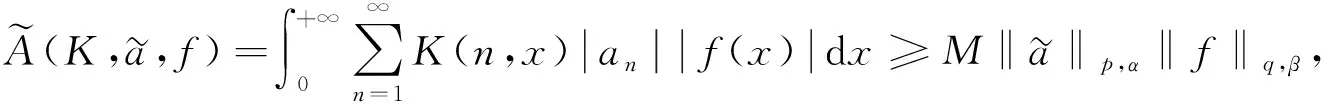

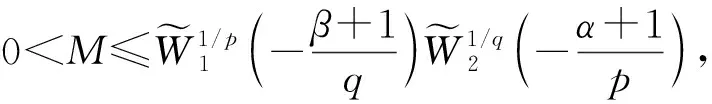

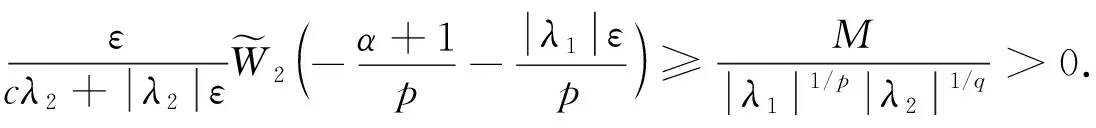



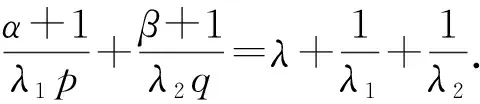


3 算子表達式