n-FI內(nèi)射復形及其性質(zhì)

原雪娟,張翠萍

(西北師范大學 數(shù)學與統(tǒng)計學院,蘭州 730070)

0 引 言

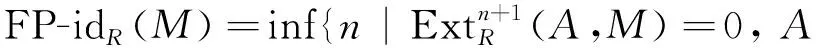
如果這樣的n不存在,則FP-idR(M)=∞.設(shè)C是左R-模的類,C∈C.如果對任意的C′∈C,HomR(C′,φ): HomR(C′,C)→HomR(C′,M)是滿同態(tài),則稱φ是M的C-預覆蓋[1];如果對任意的同態(tài)g:C→C,均有φg=φ,則g是同構(gòu),稱C-預覆蓋φ:C→M為M的C-覆蓋.對偶地,可定義C-預包絡(luò)和C-包絡(luò).

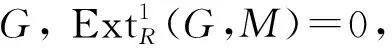
受上述結(jié)論的啟發(fā),本文將n-FI內(nèi)射模推廣到復形范疇,引入n-FI內(nèi)射復形的概念,并討論n-FI內(nèi)射復形與其層次模之間的關(guān)系,最后從覆蓋的角度刻畫n-FI內(nèi)射復形.

1 預備知識

本文用R表示有單位元的環(huán),模均指酉模,用ModR(ModRop)表示左(右)R-模范疇,表示整數(shù)集.對于R-模序列

…→0→M→0→…,

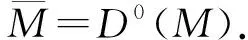
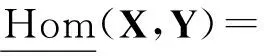
…→Exti(X,Y[n+1])→Exti(X,Y[n])→Exti(X,Y[n-1])→…,

定義1[3]設(shè)R是環(huán),n是非負整數(shù).如果對任意FP-內(nèi)射維數(shù)不超過n的左R-模X,有

則稱左R-模M是n-FI內(nèi)射模.

定義2[5]如果對任意有限表示復形A,有

Ext1(A,C)=0,

則稱復形C是FP-內(nèi)射復形.

復形X的FP-內(nèi)射維數(shù)定義為

FP-id(X)=inf{n|Extn+1(A,X)=0,A是有限表示復形,n是非負整數(shù)}.

如果這樣的n不存在,則規(guī)定FP-id(X)=∞.

定義3[4]如果對任意FP-內(nèi)射復形X,有

則稱復形C是FI-內(nèi)射復形.

引理1設(shè)X是復形,M是R-模,則:

證明: 1) 取M的內(nèi)射分解

0→M→I0→I1→….

令Ki=Ker(Ii→Ii+1),i≥0,則有復形的正合列

對偶地,可證結(jié)論2).

2 主要結(jié)果

下面設(shè)n是非負整數(shù).

顯然,0-FI內(nèi)射復形是FI-內(nèi)射復形,內(nèi)射復形是n-FI內(nèi)射復形.設(shè)m,n是非負整數(shù)且m>n,則m-FI內(nèi)射復形是n-FI內(nèi)射復形.

命題1設(shè)I是任意指標集,(Ci)i∈I是R-模的一簇復形.則∏Ci是n-FI內(nèi)射復形當且僅當每個Ci是n-FI內(nèi)射復形.

證明: 設(shè)X是復形且FP-id(X)≤n,因為

所以結(jié)論成立.

引理2設(shè)X是復形且FP-id(X)≤n,則對任意整數(shù)m,均有FP-idR(Xm)≤n.

所以FP-idR(Xm)≤n.

引理3設(shè)X是復形且FP-id(X)≤n,則對任意整數(shù)m,有FP-id(X[m])≤n.

證明: 設(shè)A是有限表示復形,則有

Extn+1(A,X[m])?Extn+1(A[-m],X)=0,

所以FP-id(X[m])≤n.

證明: 設(shè)A是有限表示復形,則由文獻[7]中引理2.2知,對任意整數(shù)m,Am-1都是有限表示模.由引理1中1)可得

定理1設(shè)C是復形,則下列結(jié)論等價:

1)C是n-FI內(nèi)射復形;

2) 對任意FP-內(nèi)射維數(shù)不超過n的復形X,有Ext1(X,C)=0;

3) 對任意整數(shù)m,Cm是n-FI內(nèi)射模,且對任意FP-內(nèi)射維數(shù)不超過n的復形X,復形Hom(X,C)正合.

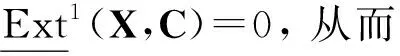
2)?1).設(shè)X是復形且FP-id(X)≤n,則對任意整數(shù)m,由引理3知,FP-id(X[m])≤n,所以有

Ext1(X,C[m])?Ext1(X[-m],C)=0,

所以Cm是n-FI內(nèi)射模.

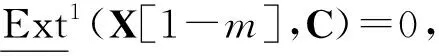
Ext1(X[1],C[m])?Ext1(X[1-m],C)=0.

令f:X→C[m]是復形的鏈映射,則有復形的可裂正合列

0→C[m]→M(f)→X[1]→0.

由文獻[8]中推論2.2知f同倫于0.從而由文獻[9]中引理2.1知,復形Hom(X,C)正合.

3)?1).設(shè)X是復形且FP-id(X)≤n,根據(jù)引理2和引理3知,對任意整數(shù)m,t,FP-idR(X[-t]m)≤n.設(shè)

0→C→Y→X[-t]→0

(1)

0→Cm→Ym→X[-t]m→0

可裂.故正合列(1)同構(gòu)于復形的正合列

0→C→M(f)→X[-t]→0,

(2)

其中f:X[-t-1]→C.由引理3知FP-id(X[-t-1])≤n,所以Hom(X[-t-1],C)正合.故f同倫于0.由文獻[8]中推論2知,正合列(2)可裂,從而正合列(1)可裂,進而

Ext1(X,C[t])?Ext1(X[-t],C)=0.

證明: 充分性.由定理1可得.

必要性.設(shè)X是復形且FP-id(X)≤n,由引理1和引理2可得

令FPn是所有FP-內(nèi)射維數(shù)不超過n的復形的類,FPn(R)是所有FP-內(nèi)射維數(shù)不超過n的模的類.

定理2設(shè)C是復形,則下列結(jié)論等價:

1)C是n-FI內(nèi)射復形;

2) 對任意復形正合列0→C→X→Y→0,X→Y是Y的FPn-預覆蓋,其中X∈FPn;

3) 存在復形B的FPn-預覆蓋f:A→B,使得C?Ker(f),其中A是內(nèi)射復形;

4) 對任意復形正合列0→A→B→X→0,0→Hom(X,C)→Hom(B,C)→Hom(A,C)→0正合,其中X∈FPn.

證明: 1)?2).設(shè)0→C→X→Y→0是復形的短正合列,其中X∈FPn.令X′∈FPn,則由定理1知Ext1(X′,C)=0,從而有正合列

Hom(X′,X)→Hom(X′,Y)→0.

因此X→Y是Y的FPn-預覆蓋.

1)?4).由定理1可得.

2)?3).取復形正合列

0→C→E(C)→E(C)/C→0,

其中E(C)是內(nèi)射復形,所以E(C)∈FPn.由2)知結(jié)論成立.

3)?1).由3)可得復形的正合列

其中A是內(nèi)射復形.從而有正合列

0→C→A→Im(f)→0.

易得A→Im(f)是FPn-預覆蓋.設(shè)X∈FPn,則有如下正合列:

因為f*是滿的,所以Ext1(X,C)=0.由定理1知C是n-FI內(nèi)射復形.

4)?1).設(shè)X∈FPn,取復形的正合列

其中B是投射復形.從而有正合列

由4)知g*是滿的,于是有

Ext1(X,C)=0.

故由定理1知,C是n-FI內(nèi)射復形.證畢.

由推論1和定理2可得以下推論.

推論2[3]設(shè)M是R-模,則下列結(jié)論等價:

1)M是n-FI內(nèi)射模;

2) 對任意R-模的正合列0→M→E→K→0,E→K是K的FPn-預覆蓋,其中E∈FPn(R);

3) 存在模B的FPn-預覆蓋h:A→B,使得M?Ker(h),其中A是內(nèi)射模;

4) 對任意R-模的正合列0→A→B→X→0,有0→Hom(X,M)→Hom(B,M)→Hom(A,M)→0正合,其中X∈FPn(R).