非飽和花崗巖殘積土的彈塑性本構(gòu)模型與驗(yàn)證

張 強(qiáng),劉一奧

(1.中國(guó)海洋大學(xué) 環(huán)境科學(xué)與工程學(xué)院,山東 青島 266000;2.山東省魯南地質(zhì)工程勘察院,山東 濟(jì)寧 272100;3.吉林大學(xué) 建設(shè)工程學(xué)院,長(zhǎng)春 130026;4.國(guó)家開(kāi)發(fā)銀行吉林省分行,長(zhǎng)春 130022)

非飽和花崗巖殘積土是一種特殊的物質(zhì)材料[1-3],具有復(fù)雜的物理力學(xué)特性.由于母巖巖脈分布不均且抗風(fēng)化能力不同,導(dǎo)致風(fēng)化的殘積土在力學(xué)性質(zhì)上表現(xiàn)出不均勻性和各向異性,其“兩頭大、中間細(xì)”的顆粒級(jí)配特點(diǎn),使花崗巖殘積土表現(xiàn)為結(jié)構(gòu)松散和透水性強(qiáng).水分進(jìn)入土后會(huì)溶解其中包裹粗顆粒土骨架的可溶鹽,導(dǎo)致土骨架損傷,進(jìn)而發(fā)生崩解現(xiàn)象.自然界中花崗巖殘積土大多呈非飽和狀態(tài),非飽和與飽和條件下土的性質(zhì)具有顯著差異,工程性狀也更復(fù)雜.針對(duì)上述問(wèn)題,在了解殘積土的特殊物質(zhì)組成、物理和力學(xué)特性基礎(chǔ)上,需構(gòu)建合理的描述方法以提高土體變形預(yù)測(cè)的可靠性.目前通常以飽和土的理論依據(jù)解決非飽和土的工程問(wèn)題,這種假設(shè)導(dǎo)致計(jì)算結(jié)果與實(shí)際工程差距較大.近年來(lái),研究人員對(duì)土的非飽和力學(xué)特性的測(cè)試和描述理論進(jìn)行了探索并取得較大進(jìn)展,提出了更合理的非飽和土的彈塑性模型,如文獻(xiàn)[4]以吸力和凈應(yīng)力為雙應(yīng)力變量提出了BBM(Barcelona basic model)模型,采用LC(loading-collapse)屈服線表達(dá)吸力對(duì)屈服應(yīng)力的硬化規(guī)律;文獻(xiàn)[5-7]以BBM模型為基礎(chǔ),提出了考慮吸力為附加應(yīng)力狀態(tài)變量的非飽和土本構(gòu)模型.這類(lèi)模型忽視了土體飽和度和孔隙率變化對(duì)土體性質(zhì)的改變.在流-固模型中,對(duì)土中水分變化的表述一般采用土-水特征曲線模型,如Brooks-Corey模型、Van Genuchten模型和Fredlund-Xing模型[8-11],這些模型可間接預(yù)測(cè)非飽和土體的滲流、強(qiáng)度和變形等性質(zhì).Wheeler等[12]以飽和度為模型參數(shù),采用雙變量理論建立了水-力全耦合模型(GCM);熊勇林等[13]基于水-土-氣三相耦合模型分析了非飽和邊坡穩(wěn)定性.在非飽和土的本構(gòu)模型和應(yīng)用研究中,由于考慮了基質(zhì)吸力和飽和度對(duì)模型性質(zhì)的影響,因此有些模型的數(shù)學(xué)形式較復(fù)雜.基于此,本文結(jié)合花崗巖殘積土的非飽和力學(xué)特性,基于修正的劍橋模型,通過(guò)調(diào)整屈服面形態(tài),將飽和度作為參數(shù)量,推導(dǎo)修正劍橋模型的基本增量格式,實(shí)現(xiàn)非飽和土的變形分析.

1 考慮非飽和特性的修正劍橋模型

在飽和土修正劍橋模型的基礎(chǔ)上提出非飽和土的修正劍橋模型,主要考慮飽和度影響的屈服面擴(kuò)展形狀,非飽和土的修正劍橋模型屈服面示意圖如圖1所示.

圖1 非飽和土的修正劍橋模型屈服面示意圖Fig.1 Schematic diagram of yield surface of modified Cambridge model for unsaturated soils

1.1 屈服面方程

非飽和土由固體顆粒及充填在顆粒間孔隙中的水和氣組成,用有效應(yīng)力表示應(yīng)力分量為

(1)

若將χ簡(jiǎn)化為飽和度Sr,則式(1)可變?yōu)?/p>

p′=(p-ua)+Sr(ua-uw),

(2)

由式(2)可知,若忽略孔隙中氣壓的影響,則非飽和土體的有效應(yīng)力與孔隙水壓力和土體的飽和度均相關(guān),其力學(xué)特性在一定程度上受土-水特征曲線影響.

在p-q平面上建立屈服軌跡方程為

(3)

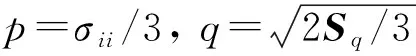
與修正劍橋模型相比,考慮了土體的抗拉屈服強(qiáng)度pt,并考慮了應(yīng)變強(qiáng)化與飽和度強(qiáng)化.式(3)與修正劍橋模型保持相同的形式.屈服面軌跡F的大小可用pc函數(shù)表示.在p-q平面內(nèi)屈服面為橢圓形(圖1),此外,圖1中還有一個(gè)與飽和度Sr有關(guān)聯(lián)的LC屈服面,為在Sr-p′平面上橢圓屈服軌跡F的交線,反映了在飽和度變化下屈服面不斷強(qiáng)化的過(guò)程[14-16].

1.2 流動(dòng)法則

為簡(jiǎn)單,采用相關(guān)聯(lián)的流動(dòng)法則.當(dāng)屈服面臨界狀態(tài)小于應(yīng)力狀態(tài)時(shí),可將塑性勢(shì)函數(shù)對(duì)應(yīng)為屈服面方程,此時(shí)應(yīng)變(塑性)的流動(dòng)方向?yàn)榇怪庇谇娌⒅赶騼?nèi)部.在此將塑性應(yīng)變?cè)隽恳暈樗苄约魬?yīng)變與體應(yīng)變?cè)隽恐蚚17].根據(jù)傳統(tǒng)塑性位勢(shì)理論,塑性體應(yīng)變與剪應(yīng)變?cè)隽康男问綖?/p>

(4)

當(dāng)采用相關(guān)聯(lián)的流動(dòng)法則時(shí),屈服面方程F與塑性勢(shì)函數(shù)Q一致.引入變量剪脹比Ds用以描述各應(yīng)變分量間的函數(shù)關(guān)系,Ds可表示為

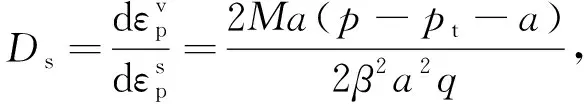
(5)

結(jié)合式(4)和式(5)可得塑性總應(yīng)變?cè)隽坑盟苄约魬?yīng)變?cè)隽康谋磉_(dá)式為

(6)

其中σij為應(yīng)力張量,A,B,C均為列向量.

對(duì)于強(qiáng)化準(zhǔn)則[18],定義為

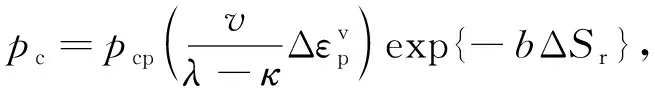
(7)

其中b為(-Sr)-lnpc直線的斜率,κ和λ分別為超固結(jié)和正常固結(jié)線的斜率,pcp為先期固結(jié)壓力.

2 增量型本構(gòu)關(guān)系推導(dǎo)

增量型模型一定程度上可避免因應(yīng)力-應(yīng)變關(guān)系的非線性所導(dǎo)致的收斂問(wèn)題,適于用戶利用商業(yè)軟件的用戶接口實(shí)現(xiàn)數(shù)值計(jì)算.考慮彈塑性材料的基本特點(diǎn),則有

{Δσ}=(De){Δεe}=(De){Δε-Δεp},

(8)

其中{Δσ}為應(yīng)力增量,{Δεe}為彈性應(yīng)變?cè)隽?{Δε}為總應(yīng)變?cè)隽?{Δε}={Δεe}+{Δεp},(De)為彈性剛度矩陣.

根據(jù)一致性條件,屈服面方程滿足等量關(guān)系

(9)

由偏應(yīng)力項(xiàng)、體應(yīng)力項(xiàng)和總應(yīng)力項(xiàng)間的關(guān)系可得式(9)中偏應(yīng)力項(xiàng)為

(10)

由式(9)和式(10)可得

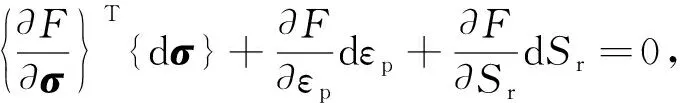
(11)

將式(8)代入式(11)可得

(12)

將dεp項(xiàng)合并,并將其系數(shù)消去可得

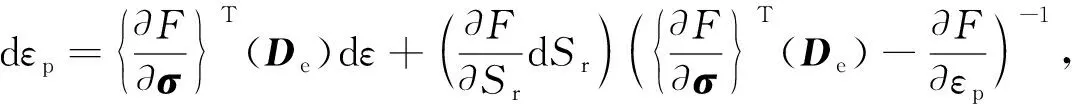
(13)

將式(13)代入式(8)并合并同類(lèi)項(xiàng)可得

{Δσ}=(De){Δε-Δεp}=(Dep){dε}+(DSr){dSr}.

(14)

由此得到應(yīng)力-應(yīng)變Jacobi矩陣和飽和度-應(yīng)力Jacobi矩陣分別為

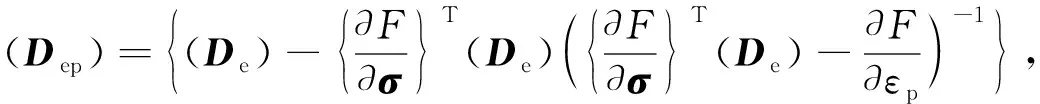
(15)

(16)

考慮應(yīng)變-飽和度耦合的計(jì)算格式,需將上述Jacobi矩陣進(jìn)行擴(kuò)展,得到修正劍橋模型的增量型本構(gòu)關(guān)系為

{dσ}=(Dw){dεw},

(17)

由于(Dw)矩陣中以飽和度Sr為變量,通過(guò)間接表達(dá)基質(zhì)吸力對(duì)力學(xué)性質(zhì)的影響,因此求解較簡(jiǎn)單.

3 模型驗(yàn)證

為驗(yàn)證模型的可靠性,采用FORTRAN編程語(yǔ)言形成用戶自定義材料力學(xué)行為(UMAT)子程序,利用ABAQUS/STANDARD求解器進(jìn)行非飽和土的應(yīng)力與變形分析,模型參數(shù)和取值列于表1.先在ABAQUS CAE(前處理工具)內(nèi)輸入材料參數(shù),再利用CAE內(nèi)置功能生成inp文件提供給ABAQUS/STANDARD求解器,由inp文件內(nèi)部的聲明命令求解器調(diào)用UMAT子程序,讀取材料參數(shù)并進(jìn)行應(yīng)力變形分析.為驗(yàn)證模型的有效性,采用室內(nèi)非飽和三軸實(shí)驗(yàn)結(jié)果進(jìn)行對(duì)比.

表1 模型參數(shù)和取值

圖2 樣品的粒徑分布曲線Fig.2 Particle size distribution curve of sample

以直徑50 mm和高度100 mm的圓柱體花崗巖殘積土為樣品,在GDS(global digital system)非飽和三軸儀上開(kāi)展三軸剪切實(shí)驗(yàn).樣品的粒徑分布曲線如圖2所示,根據(jù)《土的工程分類(lèi)標(biāo)準(zhǔn)》(GB/T50145-2007)[19],樣品中礫砂、砂粒和細(xì)粒粒組的相對(duì)質(zhì)量百分?jǐn)?shù)分別為16%,51%和33%,不均勻系數(shù)Cu=100,曲率系數(shù)Cc=0.73.在應(yīng)力150 kPa和基質(zhì)吸力分別為25,75,150 kPa下進(jìn)行實(shí)驗(yàn).在實(shí)驗(yàn)開(kāi)始前,先通過(guò)抽氣法使樣品飽和,再通過(guò)GDS非飽和測(cè)試系統(tǒng)給樣品施加5 kPa的基質(zhì)吸力使土樣進(jìn)一步飽和,使其飽和度大于95%.GDS三軸實(shí)驗(yàn)分為吸力平衡、等吸力固結(jié)和等吸力剪切破壞3個(gè)階段.在吸力平衡階段利用軸平移技術(shù),使孔隙氣壓力保持不變而改變孔隙水壓力,以此實(shí)現(xiàn)基質(zhì)吸力平衡.若反壓體積變化量在連續(xù)24 h內(nèi)不超過(guò)50 mm3,則認(rèn)為達(dá)到基質(zhì)吸力平衡.在等吸力固結(jié)階段,凈圍壓取150 kPa,固結(jié)時(shí)需確保吸力保持不變.在等吸力剪切破壞階段,控制剪切速率0.05 mm/min,軸向應(yīng)變以15%為破壞標(biāo)準(zhǔn).

由測(cè)試得到的土-水特征曲線確定花崗巖殘積土體積含水率θw和基質(zhì)吸力ψ的關(guān)系為

(18)

采用上述模型計(jì)算時(shí),考慮與三軸剪切實(shí)驗(yàn)條件相同,施加預(yù)定義孔壓場(chǎng),其大小為150 kPa,同時(shí)預(yù)設(shè)0.9的初始孔隙率.給樣品表面施加不排水邊界條件,以控制加載過(guò)程中基質(zhì)吸力.

在150 kPa凈圍壓,基質(zhì)吸力分別為25,75,150 kPa下的數(shù)值模擬與室內(nèi)實(shí)驗(yàn)數(shù)據(jù)的對(duì)比結(jié)果如圖3所示.由圖3可見(jiàn),無(wú)論是偏應(yīng)力-軸向應(yīng)變關(guān)系,還是體應(yīng)變-軸向應(yīng)變關(guān)系,在3種基質(zhì)吸力下,當(dāng)軸向應(yīng)變小于6%時(shí),預(yù)測(cè)結(jié)果與實(shí)驗(yàn)值有一定的差距,當(dāng)軸向應(yīng)變大于6%時(shí),具有良好的一致性.所建模型在模擬非飽和土的剪縮性能上具有良好的表現(xiàn).

圖3 不同基質(zhì)吸力下模型計(jì)算結(jié)果與實(shí)驗(yàn)數(shù)據(jù)比較Fig.3 Comparison between model calculation results and test data under different matrix suction

綜上所述,本文在非飽和修正劍橋模型的基礎(chǔ)上,對(duì)模型的屈服面性狀進(jìn)行了修正,并將飽和度作為參數(shù),推導(dǎo)了修正劍橋模型的增量型本構(gòu)關(guān)系.模型參數(shù)少,物理意義明確,模型計(jì)算結(jié)果與花崗巖殘積土的非飽和三軸實(shí)驗(yàn)結(jié)果一致,表明所建模型具有較好的可靠性.