“平行四邊形的面積”教學中的問題分析

江燕　郜舒竹

【摘? ?要】分析現有“平行四邊形的面積”的教學設計和課堂教學，發現教學中存在“以‘拉一拉活動導入課程不合理、‘數方格法的片面化看待和不科學規定、‘分、移、補活動中結論和剪拼方式不完備”等問題。據此，教師對問題進行分析并提出改進意見，以期完善對“平行四邊形的面積”的教學。

【關鍵詞】平行四邊形的面積；數方格；剪拼；直覺錯誤

一、以“拉一拉”活動作為導入方式的不合理性

在現有“平行四邊形的面積”的教學設計及課堂教學中，有教師會在導入環節采用“拉一拉”的操作活動［1］，讓學生通過拉動長方形模型，感知長方形被拉動后變成了平行四邊形，并將拉成的平行四邊形與原有的長方形作對比，發現圖形周長相等，面積卻在變小。將“拉一拉”這一操作活動作為本課的導入方式是否合適，值得深度思考。

首先，北師大版教材將面積定義為“物體的表面或封閉圖形的大小”。面積是對“面”的大小的度量，“面”的存在是計量面積的前提。在“拉一拉”的操作活動中，從視覺角度看，學生能觀察到圖形相鄰兩條邊之間的相對位置在改變，卻不能直觀地觀察到“面”這一屬性。沒有“面”作為前提，也就無從感知圖形面積（“面”的大小）在逐漸變小。

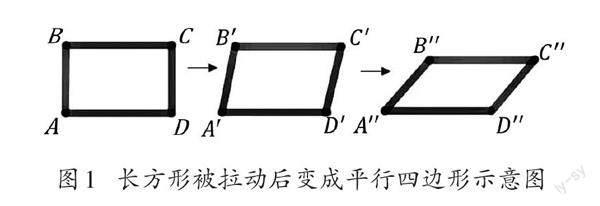
其次，如圖1所示，捏住長方形模型ABCD的一組對角向外拉，當長方形ABCD變為平行四邊形A'B'C'D'時，多數學生會認為長方形ABCD的面積與平行四邊形A'B'C'D'的面積相等，理由是向斜角凸出的部分（增加的量）和向下減少的部分（減少的量）相等，根據“量1加上量2，又減去量2，結果仍為量1”的事實，可以得出長方形ABCD與平行四邊形A'B'C'D'具有“形異量等”的等價關系，二者面積相等。

此外，學生在三年級時已獲得“長方形的面積=長×寬”的認知。從視覺上看，長與寬是長方形相鄰兩邊的長度，因此學生容易形成“長方形面積等于相鄰兩邊長度乘積”的錯誤圖式。在“拉一拉”的操作活動中，拉動的過程改變的是相鄰兩邊之間的相對位置，邊的長度并未改變，所以長方形ABCD相鄰兩邊的長度與平行四邊形A'B'C'D'相鄰兩邊的長度相等。利用有關長方形面積的認知經驗，學生自然而然就形成了“平行四邊形的面積等于相鄰兩邊長度乘積”的直覺錯誤。只有當長方形ABCD被拉成比較扁的平行四邊形A''B''C''D''時，學生才能直觀地發現圖形的周長沒有變化，面積卻在變小。

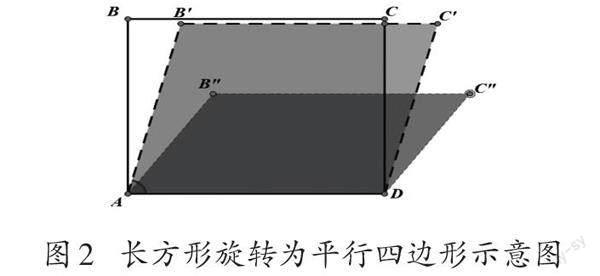
要解決學生在“拉一拉”操作活動中無法直觀感知到“面”這一問題，以及形成“平行四邊形的面積等于相鄰兩邊長度乘積”的直覺錯誤，就必須了解“面”這一屬性，同時澄清長方形ABCD與平行四邊形A'B'C'D'面積不相等。為此可以采用幾何動畫的形式，如圖2所示，以動態的眼光去看，拉動的過程實際就是長方形旋轉導致形變（變為平行四邊形）的過程，直觀來看就是長方形的寬沿順時針方向旋轉一個角度，此時邊長保持不變，但面積變小了，而且隨著旋轉的繼續，面積會越來越小。

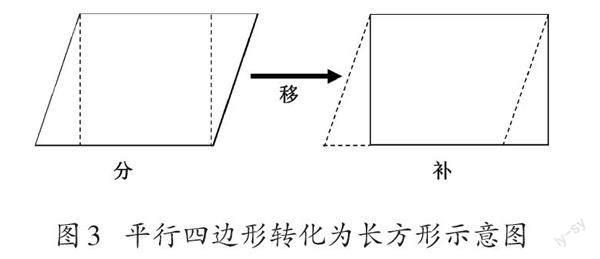
最后，通過“拉一拉”操作活動，學生得出結論：長方形被拉成平行四邊形后，其面積在變小，即此時的長方形和平行四邊形之間存在“形異量不等”的關系。然而，在推導平行四邊形的面積時，學生是通過“分、移、補”的活動將平行四邊形轉化為長方形，再借助已知長方形的面積計算公式去推導平行四邊形的面積計算公式的。此時學生得出的結論為平行四邊形與長方形的面積相等（如圖3），即此時的長方形和平行四邊形之間存在“形異量等”的關系。可見，學生在兩個活動中所得出的結論并不一致，這會導致他們思維混亂，無法真正理解平行四邊形的面積與長方形的面積之間的內在關系。

對于“拉一拉”這一操作活動，人教版教材五年級上冊“平行四邊形的面積”將其以課后習題的形式放置于練習十九中（如圖4）。此前，學生通過對教學內容的學習，已經明晰平行四邊形的面積受到底和高的制約，是底和高的乘積；同時“分、移、補”活動使學生認識到，平行四邊形的面積與長方形的面積相等的原因在于圖形間的內部因素具有一一對應的關系，即原有的平行四邊形的底與高分別轉化成了長方形的長和寬。基于以上認知經驗去解釋和說明為什么在拉動過程中圖形的面積在變小，就能避免“平行四邊形的面積等于相鄰兩邊長度乘積”的直覺錯誤以及結論不一致導致的思維混亂。

綜上所述，將“拉一拉”操作活動作為“平行四邊形的面積”教學的導入方式，有如下弊端：一是無法保證度量面積的前提——“面”這一屬性的存在；二是當捏住長方形的一組對角輕輕拉動時，學生通過直接觀察模型，無法直觀地感知面積的變化（變小），因而會認為此時圖形的周長和面積都沒有發生變化，再結合對長方形面積的認知，產生“平行四邊形的面積等于相鄰兩邊長度乘積”的直覺錯誤；三是“拉一拉”操作活動中平行四邊形與長方形之間呈現的“形異量不等”關系，與后續“分、移、補”活動中平行四邊形與長方形之間呈現的“形異量等”關系相互沖突，知識內容的不一致會導致學生思維混亂。

二、“數方格”法的片面化看待和不科學規定

面積計量的一個基本方法是單位面積度量法，在小學數學中通常也叫作“數方格”法。該方法是將一張方格紙當作一把“面積尺”（其中每個方格代表一個面積單位），通過將平面圖形平鋪于方格紙上，數出圖形含有多少個方格（面積單位的個數），以此計算圖形的面積。［2］在有關面積內容（包括平行四邊形的面積）的教學中，初始時一般都會采用“數方格”的方法來進行。但在部分“平行四邊形的面積”的教學設計中，教師認為“數方格”的方法既不好操作，又很煩瑣，與之相比，剪拼的方法易于操作且方便，因此直接摒棄“數方格”的方法，強調引導學生將平行四邊形通過剪拼的活動轉化為長方形來計算面積。［3］

那么，“數方格”法在面積教學中是否重要呢？“圖形與幾何”領域中涉及許多有關圖形面積計量（平面圖形的面積以及立體圖形的表面積）的內容。史寧中教授認為，面積度量實質就是計算該圖形包含多少個面積單位。［4］“數方格”是以方格紙作為度量面積的直觀模型，其實質就是“數”面積單位的個數，所以借助“數方格”的方法可以幫助學生理解面積是面積單位的累加，計量面積就是計量面積單位的個數。

人教版教材中仍然沿用“數方格”這一方法。在數格子的過程中，學生會遇到所數“方格”不是“整格”的情況。對此，教材的解決辦法是：不滿一格的都按半格計算（如圖5）。

然而，在實際應用中，那些不滿一格的“方格”，有些與一格十分接近，有些非常小（甚至可以忽略），全都把它們按半格計算的做法具有合理性嗎？

如圖6所示，圖中兩個平行四邊形的形狀不同，但底邊長度和高度分別相等。已知決定平行四邊形的面積的因素是底和高，所以底和高分別相等的平行四邊形的面積相等，即圖6中兩個平行四邊形的面積相等。再根據平行四邊形面積=底×高，可以計算出兩個平行四邊形的面積都為2×2.5=5（平方厘米）。

如果采用“數方格”的方法，可以數出圖6左邊的平行四邊形有2個“整格”，“不滿一格”的有7個；右邊的平行四邊形有2個“整格”，“不滿一格”的有10個。按照“不滿一格的都按半格計算”的規定，左邊的平行四邊形包含2個“整格”和7個“半格”，右邊的平行四邊形包含2個“整格”和10個“半格”。1個方格代表1平方厘米，半格就代表0.5平方厘米，從而數出左邊平行四邊形的面積為5.5平方厘米，右邊平行四邊形的面積為7平方厘米。

顯而易見，按照“不滿一格的都按半格計算”的規定，“數”出來的面積數與實際面積數之間存在不一致性，而且還是一個具有不確定性的估計值，形狀不同，數值也不同。因此，將“不滿一格的都按半格計算”的做法不科學、不嚴謹、不具合理性，學生難以接受。如果換個角度去引導學生思考：不采用“不滿一格的都按半格計算”的做法，那“整格”以外的方格（接近一格與不足半格或兩個半格）應該怎么計量？學生結合生活經驗，可能會想出通過剪拼的方式，將不足一格的方格拼在一起變成“整格”來計量，在此基礎上自然而然地引出轉化思想以及實現轉化的方法——剪拼法，從而建立“數方格”法與“轉化”之間的深度聯系。

除此之外，借助方格紙的直觀性進行“平行四邊形的面積”的教學，能幫助學生明確底和高是決定平行四邊形的面積的關鍵因素，并根據直觀得到的平行四邊形面積、底和高之間的關系，推導出平行四邊形的面積=底×高，從而實現數形結合。如圖7所示，將三個不同形狀的平行四邊形復刻于方格紙上，利用方格紙的直觀性，比較它們的底、高、面積之間的關系。比較圖①和圖②，可知平行四邊形的高相同，底越長，面積越大；比較圖②和圖③，可知平行四邊形的底相同，高越長，面積越大。因此得到決定平行四邊形面積的關鍵因素為底和高。

同樣，在圖5提及的方格紙中，一個方格代表1平方米，邊長為1米的正方形的面積為1平方米，即每個方格的邊長為1米。學生結合方格圖可以直接數出三個平行四邊形的面積、底和高，并通過將三個不同形狀的平行四邊形的面積與其對應的底和高的乘積進行比較，在數形結合中發現規律：平行四邊形的面積受制于底和高，是底和高的乘積。

三、“分、移、補”活動中結論和剪拼方式的不完備

對于“平行四邊形的面積”的推導，教材中多是引導學生通過“分、移、補”的活動，沿著高從平行四邊形中分出一個直角三角形，將其平移到另一側，然后補齊變成長方形（如圖3），此時平行四邊形的底轉化為長方形的長，高轉化為長方形的寬，結合“長方形的面積=長×寬”，推導出“平行四邊形的面積=底×高”。但教材中這樣的設計指向的只是一個特殊的平行四邊形的面積，其高位于平行四邊形內部（以下簡稱“形內高”），而對于高位于形外（以下簡稱“形外高”）的情況卻并未涉及［5］。

“形內高”平行四邊形轉化為長方形的方式是將左邊的直角三角形剪下來平移到右邊對應的位置。然而這種剪拼轉化的方法，對于“形外高”平行四邊形來說并不適用（如圖8）。

對此，學生會產生“是否平面上每一個平行四邊形都可以轉化為長方形？”“同一個平行四邊形具有不同的底邊和對應的高，其面積是否都可以用底與高的乘積來表示？”“所有的平行四邊形都是沿著高分割出一個直角三角形，平移到另一側，補齊成長方形嗎？”等疑惑。

因此，只針對“形內高”平行四邊形得出“平行四邊形的面積=底×高”的結論，在一定程度上會缺乏說服力。且將其轉化為長方形的過程中只涉及“將左邊的直角三角形平移到右邊對應的位置”的剪拼方式，可能會忽視學生自主構建多樣化的轉化方法的可能性。所以，教師應該盡可能提供多角度的材料，讓學生觀察、操作、思考，發現不同角度、不同形狀、不同大小的平行四邊形（包括“形內高”和“形外高”）都可以通過剪拼的方式轉化為長方形，剪拼的方式可以是多樣化的。在此基礎上根據平行四邊形的面積（底乘高）與轉化后的長方形的面積（長乘寬）之間建立等價關系，結合“長方形的面積=長×寬”的知識經驗，得到“平行四邊形的面積=底×高”。這種讓學生對不同類型的平行四邊形進行剪拼，并由一定的知識經驗得出的結論，才能讓學生體會到轉化方法的多樣性及結論的科學性、合理性。因此，我們要對“平行四邊形的面積”的教學進行重新認識，設計出科學、合理并有益于學生數學核心素養發展的學習活動。

參考文獻：

［1］田志明.《平行四邊形的面積》教學設計［J］.教學與管理，2013（23）：61-63.

［2］羅晉，李娜，董晶晶. 數方格法在求平行四邊形面積一課中的作用［J］.中小學數學（小學版），2020（3）：50-51.

［3］王長娥.《平行四邊形的面積》教學設計［J］.小學科學（教師版），2017（4）：94-95.

［4］史寧中.基本概念與運算法則：小學數學教學中的核心問題［M］.北京：高等教育出版社，2013.

［5］郜舒竹，李娟.平行四邊形的面積：從否認到確認［J］.教學月刊·小學版（數學），2022（12）：4-8，17.