理性思維培養(yǎng):核心素養(yǎng)下小學數(shù)學概念教學的根本
李國強 苗珠珠
【摘? ?要】數(shù)學核心素養(yǎng)指向理性思維的培養(yǎng)。數(shù)學概念是聯(lián)系數(shù)學與現(xiàn)實世界的橋梁,數(shù)學概念的習得過程蘊含豐富的理性思維,數(shù)學概念教學的根本就是培養(yǎng)學生的理性思維。核心素養(yǎng)下的小學數(shù)學概念教學,要通過“聚焦核心素養(yǎng)的主要表現(xiàn),關注理性思維;重視數(shù)學概念的建構過程,凸顯理性思維;揭示數(shù)學概念的本質,促進理性思考;注重關鍵概念的教學,實現(xiàn)理性進階;嘗試概括數(shù)學概念,強化理性表達”等策略,培養(yǎng)學生的理性思維,發(fā)展學生的核心素養(yǎng)。
【關鍵詞】核心素養(yǎng);理性思維;數(shù)學概念;概念教學
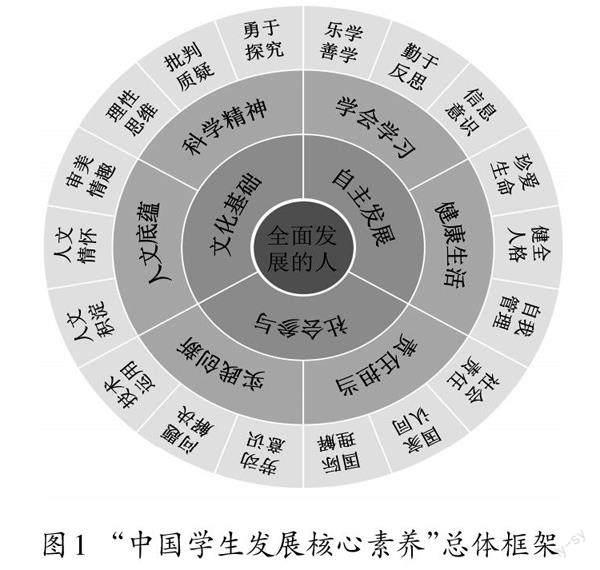
《義務教育數(shù)學課程標準(2022年版)》(以下簡稱“2022年版課標”)凸顯核心素養(yǎng),并把核心素養(yǎng)確立為數(shù)學課程目標。然而,在“中國學生發(fā)展核心素養(yǎng)”的總體框架(如圖1)中,卻不見“數(shù)學”二字。那么,數(shù)學學科在學生核心素養(yǎng)培養(yǎng)中的價值到底是什么呢?
一、數(shù)學核心素養(yǎng)指向理性思維的培養(yǎng)
數(shù)學學科具有抽象性和嚴謹性。通過數(shù)學學習,學生能夠形成重論據、有條理、合乎邏輯的思維品質,增強理性精神。本質上,這與圖1中要發(fā)展的“理性思維”是一致的。具體而言,理性思維是人們把握客觀事物本質和規(guī)律的思維活動,它具有明確的思維方向和充分的思維依據,是一種能對事物或問題進行觀察、比較、分析、綜合、抽象與概括的思維。在人形成理性思維的過程中,數(shù)學發(fā)揮著不可替代的作用。
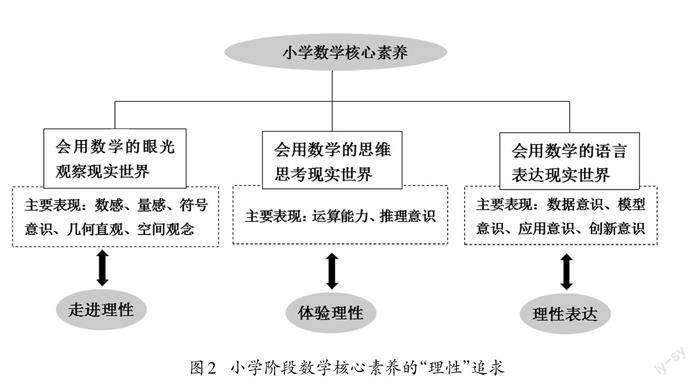
根據2022年版課標的要求,數(shù)學課程要培養(yǎng)學生的核心素養(yǎng)主要包括“三會”,即會用數(shù)學的眼光觀察現(xiàn)實世界,會用數(shù)學的思維思考現(xiàn)實世界,會用數(shù)學的語言表達現(xiàn)實世界。數(shù)學源于對現(xiàn)實世界的抽象,通過符號運算、形式推理、模型構建等,形成結論和方法,幫助人們認識、理解和表達現(xiàn)實世界的本質、關系和規(guī)律。數(shù)學知識、方法與思想的獲得需要經歷觀察、比較、分析、綜合、抽象與概括等學習活動,學習過程中處處體現(xiàn)著理性思維。從培養(yǎng)數(shù)學核心素養(yǎng)的角度看,會用數(shù)學的眼光觀察現(xiàn)實世界是“走進理性”,會用數(shù)學的思維思考現(xiàn)實世界是“體驗理性”,會用數(shù)學的語言表達現(xiàn)實世界是“理性表達”。小學階段核心素養(yǎng)的11個主要表現(xiàn),是培養(yǎng)學生理性思維的載體和抓手(如圖2)。總之,小學階段數(shù)學核心素養(yǎng)的價值追求就在于“理性”,培養(yǎng)學生的數(shù)學核心素養(yǎng)就是發(fā)展學生的理性思維。
二、數(shù)學概念的教學蘊含豐富的理性思維
數(shù)學概念是客觀現(xiàn)實數(shù)量關系和空間形式的本質屬性在人腦中的反映,是數(shù)學知識的“細胞”,是一切數(shù)學規(guī)則的基礎。
小學生一般通過概念形成和概念同化兩種方式學習數(shù)學概念。概念形成是指學生在學習數(shù)學概念的過程中,通過觀察、比較、分析具體的事物,抽象概括出該事物的本質屬性,然后將其推廣到具有這些本質屬性的某類事物中,明確事物的外延,是從具體到抽象再到具體的過程。概念同化是指基于學生原有知識經驗,通過比較、分析、綜合、概括、判斷、推理等思維活動,給一類事物下定義,以揭示其本質屬性,讓學生充分認識原有概念和新概念之間的聯(lián)系,改變原有知識的認知結構,使舊概念得到改組或改造,從而獲得新的概念。總之,學生學習數(shù)學概念的過程是從具體事物到抽象本質的過程,充滿了比較、分析、綜合、概括、判斷、推理等豐富的思維活動。
數(shù)學概念作為判斷、推理、運算和證明的基礎,是數(shù)學思維和數(shù)學交流的重要工具,因此,理解數(shù)學概念對學生學好數(shù)學至關重要。但若從學生發(fā)展的視角看,當他們從學校畢業(yè)走進社會后,很多數(shù)學概念都會被忘記,真正積淀下來、對其長遠發(fā)展發(fā)揮作用的往往是學習數(shù)學概念過程中經歷的比較、分析、綜合、抽象、概括、推理等理性思維方式。從這個層面看,數(shù)學概念本身更像是概念教學的副產品,而學生理性思維的培養(yǎng)才是數(shù)學概念教學的根本。
三、核心素養(yǎng)下小學數(shù)學概念教學中理性思維的培養(yǎng)策略
(一)聚焦核心素養(yǎng)的主要表現(xiàn),關注理性思維
核心素養(yǎng)的主要表現(xiàn)是培養(yǎng)學生理性思維的載體。因此,教師在設計教學時,不能只是簡單地關注具體知識點,還要從更高的層面關注核心素養(yǎng)的主要表現(xiàn),并以此作為教學目標組織教學。
例如,在“用字母表示數(shù)”的教學中,不僅要關注如何用字母表示數(shù),還要從符號意識的高度,讓學生經歷從數(shù)到字母的抽象、概括過程,感受數(shù)學表達的簡潔與準確;在“平均數(shù)”的教學中,不僅要關注平均數(shù)的含義與如何求平均數(shù),還要考慮數(shù)據意識的培養(yǎng),讓學生養(yǎng)成“用數(shù)據說話”的證據意識及理性思維習慣。
很多教師在教學人教版教材四年級下冊“圖形的運動(二)”中的“軸對稱”時,會把重點放在軸對稱的性質及如何補全軸對稱圖形上。而2022年版課標中的“學業(yè)要求”是“知道軸對稱圖形的對稱軸,能在方格紙上補全軸對稱圖形,形成推理意識”。因此,教師教學時,可設計諸如“你確定軸對稱圖形的依據是什么?”“補全軸對稱圖形時,為什么只要確定幾個對應點然后連起來就可以了呢?”等問題,以此引發(fā)學生思考,培養(yǎng)學生的推理意識,發(fā)展學生的理性思維。
(二)重視數(shù)學概念的建構過程,凸顯理性思維
數(shù)學概念是發(fā)展理性思維和建立數(shù)學知識體系的基本單位。數(shù)學概念的教學不僅要關注概念的內涵、外延,更要關注如何促進學生理性思維的發(fā)展,讓學生在觀察、分析、類比等思維活動中,積累抽象、概括、推理、辯證的思維經驗,提升數(shù)學理性思維水平。
在數(shù)學概念教學中,較為突出的理性思維包括抽象思維、推理思維、類比思維、辯證思維等,以下作簡要說明。
抽象思維:指舍棄物體的部分具體特征,在比較、辨析的過程中逐步得出同類事物共同的內在特征。如從文具盒、粉筆盒等實物中抽象出長方體。又如從“紅蘿卜是胡蘿卜的3倍”“黃花是藍花的3倍”“男生是女生的3倍”等具體的數(shù)量關系中,抽象出“3倍”的概念。抽象思維能使學生對事物的感性認識轉化為理性理解。
推理思維:指借助已有知識經驗對新的概念進行比較、辨析,并作出判斷。概念學習中蘊含推理思維。下面以“三角形分類”的教學片段進行說明。
(教師準備了幾個裝有三角形圖片的信封,出示其中的一個信封,只露出一個直角,讓學生猜猜里面是什么三角形)
師:里面是什么三角形?
生:我看到一個直角,這個三角形一定是直角三角形,因為有一個角是直角的三角形叫作直角三角形。
(教師出示第二個信封,只露出一個鈍角,讓學生猜猜里面是什么三角形)
師:里面是什么三角形?
生:我看到一個鈍角,這個三角形一定是鈍角三角形,因為有一個角是鈍角的三角形叫作鈍角三角形。
(教師出示第三個信封,只露出一個銳角,讓學生猜猜里面是什么三角形)
師:里面是什么三角形?
生:我看到一個銳角,這個三角形可能是直角三角形、鈍角三角形或銳角三角形,因為這些三角形中都有銳角。
師:為什么這個三角形不一定是銳角三角形呢?
生:銳角三角形必須三個角都是銳角,而我只看到了一個銳角,所以不能確定這個三角形一定是銳角三角形。
師:怎樣才能確定這個三角形一定是銳角三角形呢?
生:要看到三個銳角。
生:如果看到這個三角形最大的角是銳角,也能確定這個三角形是銳角三角形。因為連最大的角都是銳角了,那么其他兩個角也一定是銳角,這個三角形也一定是銳角三角形。
學生借助不同三角形的概念進行推理,得出信封里裝的是什么三角形,猜測、說理的過程很好地訓練了學生的推理意識。
類比思維:對于相似的新舊概念,可以運用類比思維,將相似的屬性進行比較,并借助內在邏輯,把相似屬性遷移到新的概念中。如有一位教師借助類比思維,將“長度與長度單位”的教學方法運用至“面積與面積單位”的教學中,達到了良好的教學效果。
辯證思維:客觀世界是“變與不變”的和諧統(tǒng)一,許多事物間的關系既對立又統(tǒng)一。反映客觀事物的數(shù)學概念也是如此。比如:加法、減法、乘法、除法是四種不同的運算方式,統(tǒng)稱四則運算,但四者又都可歸結為加法運算;正多邊形是直邊形,圓是曲邊形,但從極限的視角看,圓又可以看成邊數(shù)無窮多的正多邊形;等積變形中,圖形的形狀雖千變萬化,面積卻恒為定值。在概念教學中,引導學生感受不同概念中蘊含的辯證關系,既能幫助他們深刻理解概念,又能提高他們的辯證思維能力。
弗賴登塔爾說過:“與其說學數(shù)學,不如說學習數(shù)學化。”馮俊業(yè)教授進一步指出:“對學生而言,數(shù)學化就是‘從無到有、從粗糙到精致的過程。”將其引申至數(shù)學概念就是:學生學習概念,不如說是學習概念化。數(shù)學概念的教學應讓學生真切體會數(shù)學概念從無到有、從粗糙到精致的思維過程。
(三)揭示數(shù)學概念的本質,促進理性思考
數(shù)學學習依賴數(shù)學思考。如果數(shù)學概念的教學僅僅停留在表層理解與機械記憶,缺乏對數(shù)學概念本質的理解,那么概念教學就已經失去了它最本質的價值,理性思維培養(yǎng)也就無從談起。
在教學數(shù)學概念時,教師應創(chuàng)造條件,引導學生深度思考“3W”:為什么要學習數(shù)學概念(why)?數(shù)學概念的內涵是什么(what)?該概念在數(shù)學知識體系中處于怎樣的地位(how)?例如,在“認識方程”的教學中,除了讓學生理解方程的定義和兩個要素(含有未知數(shù)、等式),會識別方程,還要體現(xiàn)方程的本質,即數(shù)量(包括已知數(shù)和未知數(shù))之間的等量關系(“結構性觀念”),讓學生認識到等號不僅具有指向作用,還體現(xiàn)為等量關系。在“扇形統(tǒng)計圖”的教學中,要引導學生思考:有了條形統(tǒng)計圖、折線統(tǒng)計圖,為什么還要學習扇形統(tǒng)計圖?為什么是扇形,而不是其他形狀的統(tǒng)計圖?在“比”的教學中,要引導學生思考:已經學習了分數(shù)、除法,為什么還要學習比?分數(shù)、除法、比之間有什么區(qū)別和聯(lián)系?足球比賽中的1∶2與數(shù)學中的1∶2是一回事嗎?等等。
在對數(shù)學概念的內涵與外延、數(shù)學概念的學習價值及相關概念內在聯(lián)系等的深度思考中,學生對數(shù)學概念本質的理解更加深刻,對數(shù)學概念蘊含的理性思維的體驗也更透徹。
(四)注重關鍵概念的教學,實現(xiàn)理性進階
關鍵概念可以把教學主題內零散的知識聯(lián)系起來,體現(xiàn)教學主題的內在本質,促進知識和方法的遷移,使學生體會到概念之間的關聯(lián)互通,從而提升理性思維層次。同時,重視關鍵概念的教學還能實現(xiàn)觸類旁通,達到“教是為了不教”的效果,進而切實減輕學生的學業(yè)負擔。
例如,在數(shù)概念的教學中,教師要借助計數(shù)單位,突出整數(shù)、小數(shù)、分數(shù)之間數(shù)的概念的一致性,引導學生用整體的、聯(lián)系的、發(fā)展的眼光看問題,用數(shù)學的思維思考問題。同樣,在量概念的教學中,教師要借助計量單位,溝通長度、面積、體積以及角度等概念,讓學生在形成量感的同時,感悟量的概念的一致性。不管是角的度量,還是長度、面積和體積的度量,量都是借助數(shù)來表達的,都是計量物體含有計量單位的個數(shù)。由此可見,數(shù)概念與量概念具有一致性。
關鍵概念將零散的數(shù)學概念,依據共同的數(shù)學本質構建起富有整體化、系統(tǒng)化、邏輯化的知識體系,促進學生的思維進階,進而發(fā)展核心素養(yǎng)。
(五)嘗試概括數(shù)學概念,強化理性表達
會用數(shù)學語言表達是數(shù)學核心素養(yǎng)的“三會”之一,教師要重視培養(yǎng)學生利用數(shù)學語言描述和分析概念的能力。在數(shù)學概念的教學中,教師要引導學生通過觀察、猜測等方式嘗試描述概念,將自身的理解與概念本質進行多次對比,在逐步矯正的過程中,體會數(shù)學概念的簡明性與嚴謹性。學生“嘗試描述—揭示概念”的語言表達過程,既是將感知的概念特征內化為認知的建構過程,也是逐步舍棄事物的非本質屬性而突出本質屬性的理性表達過程。
例如,在“質數(shù)與合數(shù)”的教學中,教師先列出1~20各數(shù),引導學生對這些數(shù)進行分類。當有學生提出可根據因數(shù)個數(shù)進行分類時,教師便讓他們充分表達想法,充分經歷概念的理性表達過程。下面是該教師的教學片段。
師:(教師用手指著2、3、5、7……)請大家認真觀察,這些數(shù)的因數(shù)個數(shù)有什么共同的特征?
生:這些數(shù)都有兩個因數(shù)。(板書:兩個因數(shù))
生:我要補充。這些數(shù)的因數(shù)只有1和它本身。
生:我同意第二個同學說的。這些數(shù)的因數(shù)只有1和它本身,說明這些數(shù)只有兩個因數(shù),除了1和它本身外沒有別的因數(shù)。(板書:1和它本身)
師:誰明白他的意思?
(再讓幾名學生進行表達)
師:看來我們得加上“只有”二字。
(教師用彩色粉筆在板書中加上“只有”二字)
師:在數(shù)學中,像這樣的數(shù)叫質數(shù),也叫素數(shù)。你能跟同桌說說什么叫質數(shù)嗎?
師:自然數(shù)中,很多數(shù)的因數(shù)個數(shù)并非只有兩個,如4、6、9,它們的因數(shù)個數(shù)是……
生:不是只有1和它本身,至少有三個因數(shù)。
生:也就是說,這些數(shù)除了1和它本身外還有其他因數(shù)。
師:誰理解他說的意思?
生:比如4這個數(shù),它有三個因數(shù),除了1和本身的4以外,還有一個因數(shù)是2。
生:像6、8、9這幾個數(shù),它們都有除了1和本身以外的其他因數(shù)。
師:一個數(shù),如果除了1和它本身外,還有其他的因數(shù),這樣的數(shù)就叫合數(shù)。你能跟同桌說說怎樣的數(shù)是合數(shù)嗎?
語言是思維的外顯,是理性思維的觀念載體。引導學生用語言描述進行推理的過程,不僅能使學生加深對概念的理解,體會數(shù)學概念的簡潔、嚴謹,更能提高學生運用數(shù)學語言合乎邏輯地討論和判斷的能力,從而鍛煉理性思維。
2022年版課標的亮點之一是提出了數(shù)學核心素養(yǎng)。數(shù)學核心素養(yǎng)指向理性思維培養(yǎng)。數(shù)學概念的教學過程中蘊含著豐富的理性思維,數(shù)學概念的教學就是培養(yǎng)學生理性思維的過程。在以后的概念教學中,希望教師們重視學生的理性思維培養(yǎng),并不斷嘗試探索小學數(shù)學概念教學的新路徑,讓核心素養(yǎng)真正在教學實踐中落地生根、開花結果。
參考文獻:
[1]中華人民共和國教育部.義務教育數(shù)學課程標準(2022年版)[M].北京:北京師范大學出版社,2022.
[2]林崇德.21世紀學生發(fā)展核心素養(yǎng)研究(修訂版)[M].北京:北京師范大學出版社,2021.
[3]黃鵬,熊衛(wèi).立足思維教學 落實學科核心素養(yǎng):初中物理“認識浮力”的教學實踐與反思[J].物理教學探討,2022,40(1):73-77.
[4]董海濤,李響.數(shù)學核心素養(yǎng)視角下基于理性思維的教學設計與反思:以“數(shù)系的擴充與復數(shù)的引入”為例[J].數(shù)學通訊,2020(10):17-20.
[5]劉兆偉.建構數(shù)學概念 發(fā)展數(shù)學眼光:“倍的認識”教學片段與思考[J].小學數(shù)學教育,2021(18):46-47.
[6]林武.小學數(shù)學概念教學:行與思[M].北京:教育科學出版社,2014.
[7]周禎祥,胡澤洪.邏輯導論:理性思維的模式、方法及其評價[M].廣州:廣東高等教育出版社,2004.
[8]曹才翰,章建躍.數(shù)學教育心理學[M].北京:北京師范大學出版社,1999.

