經(jīng)歷統(tǒng)計過程，提升數(shù)據(jù)意識
——以五年級上冊“擲一擲”教學為例

浙江杭州市濱江實驗小學（310051） 張 華

《義務教育數(shù)學課程標準（2022 年版）》明確指出，“統(tǒng)計與概率”是義務教育階段數(shù)學學習的重要內(nèi)容之一，在小學階段包括“數(shù)據(jù)分類”“數(shù)據(jù)的收集、整理與表達”和“隨機現(xiàn)象發(fā)生的可能性”三個主題。其中，“數(shù)據(jù)的收集、整理與表達”涵蓋了數(shù)據(jù)的收集能力和使用統(tǒng)計圖表、平均數(shù)、百分數(shù)來表達數(shù)據(jù)的能力。通過這些主題，學生將親身經(jīng)歷數(shù)據(jù)收集的過程，并能夠發(fā)現(xiàn)其中蘊含的有價值的數(shù)學信息，從而初步形成數(shù)據(jù)意識。

如何在“統(tǒng)計與概率”這個知識板塊中培養(yǎng)學生的數(shù)據(jù)意識是一線教師一直在思考的問題。傳統(tǒng)教學往往強調(diào)數(shù)據(jù)的結果和程序化的計算過程，而忽視了數(shù)據(jù)結果的猜想、實驗數(shù)據(jù)的收集、數(shù)據(jù)的分析與驗證，以及最終得出確定性理論的完整統(tǒng)計實驗過程。這種教學方法雖然能使學生掌握概率統(tǒng)計的計算過程與結論，但卻讓課堂缺少了猜想、實驗、驗證、結論推導等學習活動。因此，需要改變這種“重數(shù)據(jù)結果，輕經(jīng)歷過程”的教學方式。下面將以人教版教材五年級上冊“擲一擲”教學為例，說明“重歷統(tǒng)計過程”對培養(yǎng)學生數(shù)據(jù)意識的重要性。

“擲一擲”是一節(jié)數(shù)學實踐活動課，其設計旨在讓學生積極參與統(tǒng)計過程，分析實驗采集的數(shù)據(jù)，合理推理與解釋數(shù)據(jù)分析的結果，并經(jīng)歷猜想、實驗、驗證、得出結論的過程。通過這個過程，學生能夠發(fā)展數(shù)據(jù)意識，提高數(shù)據(jù)分析能力，在玩樂的過程中獲得數(shù)學知識，提升數(shù)學素養(yǎng)。下面將對教學中的幾個環(huán)節(jié)進行闡述，說明如何讓學生更加重視統(tǒng)計過程，以提高他們的數(shù)據(jù)意識。

一、驗證猜想，體會數(shù)據(jù)收集的必要性

為了讓學生經(jīng)歷一個良好有效的數(shù)學學習過程，教師需要創(chuàng)設與學生生活密切相關且能引發(fā)學生興趣的數(shù)學情境。這些情境要能夠引起學生思維上的沖突，激發(fā)他們的求知欲。在情境中，猜想和驗證成為極為關鍵的解決問題的方法，它們能夠激發(fā)學生主動參與和積極探究。

課始，教師簡單介紹了骰子的知識以后，提出和學生玩一個游戲，并出示游戲規(guī)則（如圖1）。

圖1

學生在對游戲公平性的探討過程中感受到骰子六個面出現(xiàn)的可能性是一樣的，并得出“所占投擲結果情況多的一方更占優(yōu)勢”的結論。這符合學生的生活經(jīng)驗，也為后面在“兩顆骰子”的游戲中產(chǎn)生認知沖突做了鋪墊。

教師再出示“兩顆骰子”游戲的規(guī)則（如圖2），讓學生猜想A、B兩組中哪一組贏的可能性更大。

圖2

學生根據(jù)自己的經(jīng)驗進行猜測，出現(xiàn)了兩種看法。這時，教師可追問：“如何才能知道哪一組贏的可能性大？誰的猜想是對的呢？”學生馬上提出要做實驗。

在猜想與驗證的推動下，學生主動進行數(shù)據(jù)的收集、整理和分析。在這個過程中，學生深刻體驗到統(tǒng)計實驗數(shù)據(jù)對問題解決的重要性，逐漸掌握數(shù)據(jù)分析的步驟，也逐漸形成數(shù)據(jù)意識。

二、實驗統(tǒng)計，體驗數(shù)據(jù)出現(xiàn)的隨機性

分析推斷性數(shù)據(jù)的目的是通過數(shù)據(jù)推斷出產(chǎn)生這些數(shù)據(jù)的背景情況。在進行調(diào)查和實驗之前，人們通常不知道數(shù)據(jù)的確切數(shù)值，即數(shù)據(jù)的出現(xiàn)具有一定的隨機性。

因此，本節(jié)課設計了兩個不同層次的活動，旨在幫助學生深切體驗數(shù)據(jù)出現(xiàn)的隨機性。從擲一顆骰子到擲兩顆骰子，從單獨描述擲一個骰子的結果到小組成員輪流擲兩顆骰子，逐步擴展到學生對不確定現(xiàn)象和可能性大小的認識，引導學生發(fā)現(xiàn)“每次擲骰子得到的點數(shù)和都是不確定的”這一現(xiàn)象，從而真切地體驗了數(shù)據(jù)出現(xiàn)的隨機性。

筆者提供了相應的活動要求（如圖3）和統(tǒng)計記錄單（如圖4）。圖5為4個小組的實驗結果。

圖3

圖4

圖5 學生小組作品

學生通過20 次實驗得出了一些初步的結論。觀察實驗結果時，個別學生注意到中間數(shù)字的“和”出現(xiàn)的頻率較高，而兩邊數(shù)字的“和”出現(xiàn)的頻率較低（這種趨勢還不夠明顯，可能是因為實驗次數(shù)相對較少）。在這一過程中，學生已經(jīng)初步感受到了統(tǒng)計與概率的魅力。不同小組的反饋結果也讓學生認識到統(tǒng)計結果可能因數(shù)據(jù)采樣的不同而有所差異。一些小組甚至出現(xiàn)了B 組獲勝的情況，這使得課堂教學更加有趣。通過這些實驗數(shù)據(jù)，學生再次深刻體驗到了數(shù)據(jù)出現(xiàn)的隨機性。

理論上，根據(jù)部分數(shù)據(jù)可以推斷整體情況，但部分數(shù)據(jù)可能受到隨機因素的影響，因此得出的結論可能存在偏差。這為后續(xù)概率統(tǒng)計的理論教學奠定了基礎。

三、觀察分析，感受數(shù)據(jù)背后的規(guī)律性

《義務教育數(shù)學課程標準（2022 年版）》對數(shù)據(jù)意識的描述強調(diào)了以下幾點：首先，學生應該認識到，在現(xiàn)實生活中很多問題需要進行調(diào)查研究并收集相關數(shù)據(jù)，以便理解數(shù)據(jù)中所蘊含的信息；其次，學生應該明白，即使是相同的事物，每次收集到的數(shù)據(jù)也可能會有差異，但只要有足夠的數(shù)據(jù)，就有可能發(fā)現(xiàn)規(guī)律和趨勢。

在“擲一擲”教學中，為了讓學生對數(shù)據(jù)做出更加合理的判斷，筆者用Excel 表格匯總了各個小組的實驗數(shù)據(jù)（見表1），并提問：“觀察這些數(shù)據(jù)，你有什么發(fā)現(xiàn)？”

表1 學生小組的實驗數(shù)據(jù)

學生觀察后進行總結：點數(shù)之和越靠近中間的數(shù)，擲出它的次數(shù)越多。為了讓學生對部分數(shù)據(jù)的隨機性以及整體的規(guī)律性有更加深刻的了解，教師在肯定學生發(fā)現(xiàn)的同時追問：“在有些小組的數(shù)據(jù)中，為什么會出現(xiàn)擲出兩邊的數(shù)的次數(shù)比擲出中間的數(shù)的次數(shù)多的情況？”有學生說：“因為實驗的次數(shù)太少了。”教師可繼續(xù)追問：“那怎么辦？”從而引導學生想到將全班的數(shù)據(jù)進行匯總來找整體的規(guī)律性。

教師使用Excel表格等工具來統(tǒng)計各個小組的數(shù)據(jù)并生成統(tǒng)計表和統(tǒng)計圖（如圖6），這一過程可以不斷地引導學生發(fā)現(xiàn)規(guī)律。隨著數(shù)據(jù)的增加，學生可以觀察到統(tǒng)計圖的形狀趨于穩(wěn)定——形成明顯的“山”狀圖形。這有助于學生深刻體驗到：隨著數(shù)據(jù)量的增加，數(shù)據(jù)中的某種規(guī)律逐漸浮現(xiàn)。這種體驗讓學生更全面地理解了數(shù)據(jù)的整體性，并對數(shù)據(jù)分析有了更加完整的認識。

在輸入數(shù)據(jù)的過程中，教師不斷地引導學生發(fā)現(xiàn)“隨著數(shù)據(jù)的增加，統(tǒng)計圖的‘山’狀越來越穩(wěn)定”的規(guī)律（如圖7）。

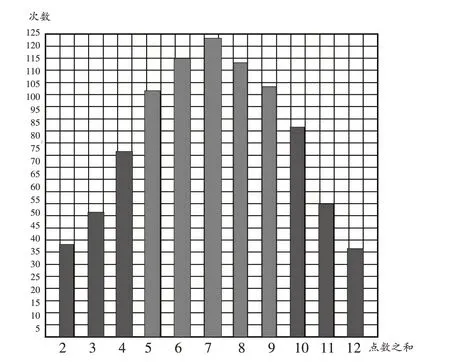
圖7 實驗1000次“兩顆骰子的點數(shù)之和”出現(xiàn)的情況統(tǒng)計圖

在實際的教學過程中，由于數(shù)據(jù)還不夠多，因此仍然可能會出現(xiàn)圖6中“點數(shù)之和為12出現(xiàn)的次數(shù)多于點數(shù)之和為11”的情況。在這種情況下，教師可向?qū)W生提出問題：“為什么會出現(xiàn)這樣的情況？”通過這種引導，學生會逐漸認識到，數(shù)據(jù)具有隨機性，因為沒有足夠多的數(shù)據(jù)，所以偶然性事件仍然會發(fā)生，不過，這種偶然性事件發(fā)生的機會會隨著數(shù)據(jù)量的增加而逐漸減少。這將激發(fā)學生主動探索的欲望，鼓勵他們積極尋求更多的數(shù)據(jù)，以便更全面地探索規(guī)律。

四、歸納推理，感悟數(shù)據(jù)出現(xiàn)的必然性

透過現(xiàn)象看本質(zhì)，數(shù)學的學習最終需要深入探究數(shù)學的本質(zhì)。當已有的經(jīng)驗和實驗結果產(chǎn)生沖突時，這種沖突可以引導學生進行質(zhì)疑，并促使他們提出問題，如“為什么會出現(xiàn)‘點數(shù)之和出現(xiàn)的次數(shù)兩邊低中間高’的情況？”這能引起學生繼續(xù)深入探究數(shù)學本質(zhì)的渴望，激發(fā)他們積極思考。在每次教學中，都會有學生在這一環(huán)節(jié)中認識到“每個點數(shù)之和出現(xiàn)的概率是不同的，這與數(shù)字的組合方式有關”。 當學生提到點數(shù)之和為2 和12 的數(shù)字組合情況的唯一性時，教師可以通過板書引導學生完成其他點數(shù)之和的數(shù)字組合情況。在反饋的過程中，一些學生甚至能對圖2 中A 組和B 組獲勝條件的點數(shù)之和的數(shù)字組合情況進行綜合總結（如圖8-1、8-2）。

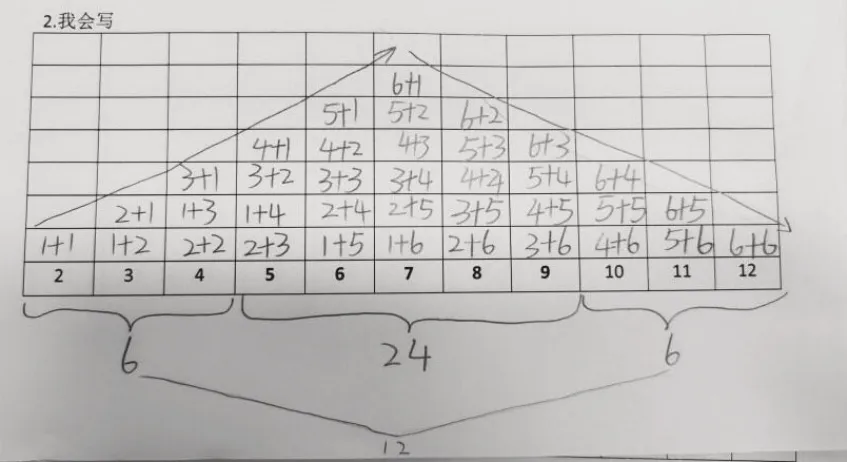
圖8-1

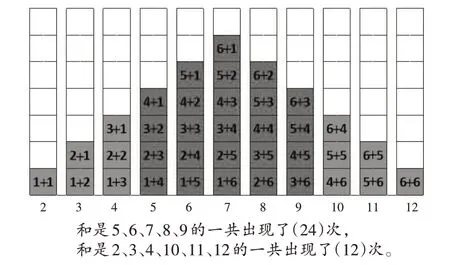
圖8-2

從數(shù)據(jù)分析到探究原因，從實踐操作到理論分析，這一過程是學生自己的實驗數(shù)據(jù)“推動”著學生思考，是學生主動的探究和發(fā)現(xiàn)。學生還發(fā)現(xiàn)他們所得的整班數(shù)據(jù)的統(tǒng)計圖與通過分析數(shù)的組合情況所得的表格之間，在形狀上存在驚人的相似之處。這使學生感悟到：任何不確定事件背后都有一定的規(guī)律可循，即使是偶然性事件，其中也包含著必然因素。這種認識在一定程度上有助于學生分析生活中的不確定事件。

小學數(shù)學教材編排了一些讓學生進行歸納推理的內(nèi)容，但大多涉及計算公式的推導，如各種平面圖形的面積公式等。像本課這種從自己實驗得出的數(shù)據(jù)出發(fā)，通過部分數(shù)據(jù)推斷整體結果的情況，是具有統(tǒng)計意義的推理，對學生來說確實是一次難得的經(jīng)歷。

要培養(yǎng)學生的數(shù)據(jù)意識，就要讓他們多次參與統(tǒng)計，親身經(jīng)歷猜想、實驗、數(shù)據(jù)收集和數(shù)據(jù)分析的過程。在這個過程中，教師可以利用多媒體和現(xiàn)代技術手段幫助學生更深刻地理解數(shù)據(jù)，引導學生感受數(shù)據(jù)分析的必要性，幫助學生在不斷質(zhì)疑、驗證和探究中，建立和發(fā)展數(shù)據(jù)意識，這具有非常重要的現(xiàn)實意義。