2023 年高考之橢圓考點解讀
■河南省許昌市高中數學胡銀偉名師工作室 胡銀偉
從近年高考命題情況來看,對橢圓定義、標準方程、幾何性質的考查常以選擇題、填空題的形式出現,而直線與橢圓的位置關系主要出現在解答題中。同學們應能夠熟練從“數”與“形”兩個角度來探究橢圓的取值范圍、對稱性、頂點、離心率等幾何性質,且熟練利用代數法解答直線與橢圓有關的最值、定點、定值等問題。下面我們結合2023年高考真題,對橢圓的考點進行解讀。
動力特性分析模型中,橋面板采用板單元模擬,其余桿件采用梁單元模擬,鋪裝和護欄等作為荷載模擬,全橋共劃分節點數量361個,梁單元數量626個,板單元數量264個。
考點1 對橢圓的方程及簡單幾何性質的考查
例1(1)【2023 年全國甲卷文數第7題】設F1,F2為橢圓的兩個焦點,點P在橢圓C上,若,則|PF1|·|PF2|=( )。
2.2.1 評價單元劃分 采用土壤圖、土地利用現狀圖和行政區劃圖的空間疊加,共劃分16 536個評價單元。
A.1 B.2 C.4 D.5
設F1到AB的 距 離 為d1,F2到AB的距離為d2,易知,則
2.2.3 專家意見的協調程度 在變異系數方面,第1輪3級指標共59個,變異系數<0.5的3級指標有52個,占88%。第2輪的3級指標變異系數均<0.5。
古希臘締造出了眾多優秀的哲學家,蘇格拉底就是當時非常突出的一位。他開創了“倫理哲學”,標志著哲學上的一種轉變,從此,人們不但研究自然,而且更多地將重心放在研究人類自身上。另一個重要的哲學家就是柏拉圖,他在哲學方面的地位和影響力在雅典乃至世界上都相當巨大。柏拉圖是蘇格拉底的學生,是亞里土多德的老師,亞里土多德與柏拉圖是西方哲學界最有影響力的兩個人,柏拉圖主張形而上學的觀念,而亞里土多德更注重從感官獲得認知和知識。
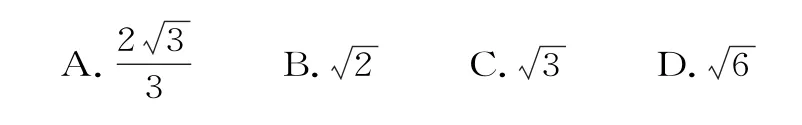
(3)【2023年全國甲卷理數第12題】設O為坐標原點,F1,F2為橢圓C的兩個焦點,點P在橢圓C上,cos∠F1PF2=,則|OP|=( )。
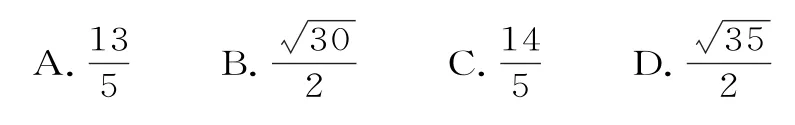
命題意圖:本例的3 個題目都是考查橢圓的方程及簡單的幾何性質,考查同學們邏輯推理、直觀想象及數學運算等核心素養。
解題思路:(1)方法一,根據焦點三角形面積公式求出△PF1F2的面積,即可求解;方法二,可根據橢圓的定義及勾股定理進行解答。(2)由給定的橢圓方程,結合離心率的定義進行解答。(3)方法一,根據焦點三角形的面積公式求出△PF1F2的面積,可得點P的坐標,從而得|OP|的值;方法二,先利用橢圓的定義及余弦定理求出|PF1|·|PF2|,|PF1|2+|PF2|2的值,再結合中線的向量公式及數量積可得解;方法三,先利用橢圓的定義及余弦定理求出|PF1|2+|PF2|2的值,再根據中線定理求解。


考點解讀:在本例(1)、(3)的解答過程中,有效地利用了橢圓中焦點三角形的面積公式的二級結論,使得問題易解。
例3【2023 年全國乙卷文數第21題】已知橢圓C的離心率是,點A(-2,0)在橢圓C上。
命題意圖:本例考查直線與橢圓的位置關系、點到直線的距離及與橢圓有關的三角形的面積,同時考查同學們直觀想象、邏輯推理及數學運算等核心素養。
隨著社會發展進步,以及環境污染等各種因素影響下,肺部真菌感染發生率呈持續性上升發展趨勢,對患者的正常生活、生活質量以及身心健康均造成較嚴重影響。肺部真菌感染患者主要癥狀包括疼痛、原發癥狀發熱以及不同程度的呼吸困難等,且無特異性,因此早期診斷、早期治療該疾病的難度較大。采取何種檢查方法可以更有利于早期診斷、早期有效鑒別肺部真菌感染,以提高臨床治療效果十分重要。本次研究工作旨在探討CT在診斷與鑒別肺部真菌感染中的可行性研究。現報道如下。
(2)涉及焦點三角形面積,可把|PF1|,|PF2|看作一個整體,運用|PF1|2+|PF2|2=(|PF1|+|PF2|)2-2|PF1|·|PF2|及余弦定理求出|PF1|·|PF2|,無須單獨求解。
與橢圓有關的二級結論比較多,由本例(1)、(3)的解答過程可以看出,恰當地掌握、應用常用的二級結論可為我們的解題打開便利之門。
考點2 對直線與橢圓位置關系的考查
因為直線與橢圓相交于A,B點,所以Δ=36m2-4×4(3m2-3)=48-12m2>0,解得-2 (1)橢圓的定義具有雙向作用,若|MF1|+|MF2|=2a(2a>|F1F2|),則點M的軌跡是橢圓;反之,橢圓上任意一點M到兩焦點的距離之和必為2a。 解題思路:首先聯立直線方程與橢圓方程,利用Δ>0,求出m的取值范圍,再根據三角形面積比得到關于m的方程,從而得解。 例2【2023 年全國新課標Ⅱ卷第5題】已知橢圓C:的左、右焦點分別為F1、F2,直線y=x+m與橢圓C交于A,B兩點,若△F1AB面積是△F2AB面積的2倍,則m=( )。 如果我們還生活在一百年前的上海灘、一百五十年前的美國西部,或者兩百年前的霧都倫敦,對于大部分人來說,是必須教孩子打回去的。一方面在一個混亂的年代,信奉的是力量至上的原則,整個社會的法則就是如此,因此必須從小讓孩子了解并且適應這樣的環境,才能在以后的生活中有更強的生存能力。“打回去”是這種崇尚暴力年代的必修課。 考點解讀:解答直線與橢圓相交的問題,常用到“設而不求”的方法,即聯立直線和橢圓的方程,消去y(或x)得到一元二次方程,然后借助根與系數的關系,并結合題設條件,建立有關參變量的等量關系求解。利用公式計算直線被橢圓截得的弦長是在方程有解的情況下進行的,不要忽略方程根的判別式。 橢圓定義在焦點三角形中的應用技巧如下。 (1)求橢圓C的方程; (2)過點(-2,3)的直線交橢圓C于P,Q兩點,直線AP,AQ與y軸的交點分別為M,N,證明:線段MN的中點為定點。 命題意圖:本例是考查與橢圓有關的定點問題,考查同學們邏輯推理、直觀想象及數學運算等核心素養。 解題思路:(1)依題意列式求解a,b,c,進而得結果;(2)設直線PQ的方程,進而可求點M,N的坐標,結合韋達定理驗證為定值即可。 CMV感染是艾滋病患者最常見的皰疹病毒感染,可分為CMV血癥和器官受累的CMV病。CMV可侵犯患者多個器官系統,包括眼睛、肺、消化系統、中樞神經系統等,其中CMV視網膜脈絡膜炎是艾滋病患者最常見的CMV感染。 (2)由題意知,直線PQ的斜率存在,設PQ:y=k(x+2)+3。 所以線段MN的中點是定點(0,3)。 截至2016年底,我國已并網發電的秸稈直燃發電項目近260個,累計并網裝機容量約為6400MW。主要分布在山東省、安徽省、黑龍江省、江蘇省、河北省、湖北省、吉林省、河南省、湖南省、山西省。 考點解讀:近年高考命題對圓錐曲線中的定點、定值問題考查較多,是近年高考命題的熱點,且常考常新,試題綜合性較強,難度較大。圓錐曲線中定點問題的常用解法:(1)引進參數法,引進動點的坐標或動直線中系數為參數表示變化量,再研究變化的量與參數何時沒有關系,找到定點;(2)特殊到一般法,根據動點或動直線的特殊情況探索出定點,再證明該定點與變量無關。圓錐曲線中定值問題的常用解法:(1)從特殊入手,求出定值,再證明這個值與變量無關;(2)直接推理、計算,并在計算推理的過程中消去變量,從而得到定值。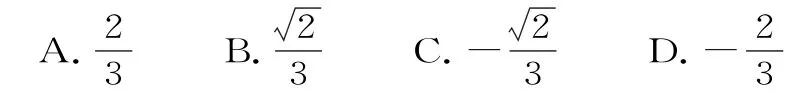

考點3 對橢圓的綜合應用的考查


