情境創設為數學學習賦能

王磊

在初中數學教學中，情境創設是一種非常重要的方法，教師要靈活創設多樣化的問題情境，如視聽情境、游戲情境、操作情境等，讓學生全身心投入數學學習中，加強數學學習體驗，發展數學思維，提升解決問題的能力。

創設視聽情境，促進直觀感知。教師將多媒體信息技術引入教學，可以豐富課堂教學形式，讓學生更好地理解知識。教學“直線和圓的位置關系”時，筆者先用課件呈現“太陽在清晰的地平線上露出可愛笑臉”的視聽情境，并將這種美麗的景象形象地比喻為直線和圓的關系。然后，筆者播放《日光曲》作為伴奏，在舒緩、優美的音樂伴隨下，“一輪紅日，從地平線上冉冉升起……”的散文詩朗誦輕輕播放出來。在視聽情境下，筆者順勢引導學生思考：直線和圓有幾個公共點？它們的位置關系可分為幾種類型？分類的依據是什么？學生認真觀察畫面，很快回答出：直線和圓有0個、1個或2個公共點，直線和圓的位置關系依據公共點個數可分三種類型，分別是相離、相切、相交。最后，筆者借助幾何畫板，讓學生通過觀察，分別比較直線與圓相離、相切、相交時圓心到直線的距離，以及它們圓半徑之間的數量關系。學生借助幾何畫板呈現的直觀圖，很快發現：相離時，這個距離大于半徑；相切時，這個距離等于半徑；相交時，這個距離小于半徑。通過視聽情境，學生學會運用聯想、數形結合的思想方法探究問題的本質，并且探究興趣高漲。

創設游戲情境，強化學習體驗。數學游戲中蘊含著數學知識、數學思維，可以增強數學學習的趣味性，讓學生在主動參與的過程中潛移默化地掌握數學知識、技能和思想方法，獲得基本數學活動經驗。

教學《中心對稱》時，筆者先帶領學生復習中心對稱的概念和性質以及中心對稱圖形的概念，進一步強化學生的尺規作圖能力。學生在回顧中明確：中心對稱指把一個圖形繞著某一點旋轉180°，如果它能夠與另一個圖形重合，就說明這兩個圖形關于這個點對稱或中心對稱，這個點叫做對稱中心；中心對稱圖形指把一個圖形繞著某一個點旋轉180°，如果旋轉后的圖形能夠與原來的圖形重合，那么這個圖形叫做中心對稱圖形，這個點就是它的對稱中心。

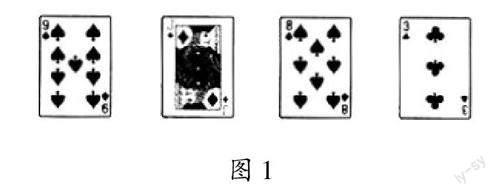
然后，筆者設計了師生互動的小游戲，讓學生在參與過程中鞏固、深化相關知識。如圖1所示，筆者把4張撲克牌放在一張桌子上，并表示：“我閉上眼睛，你可將其中任意1張撲克牌旋轉180°后放回原位，我馬上就能猜出你旋轉了哪一張。”學生興趣高漲，躍躍欲試。

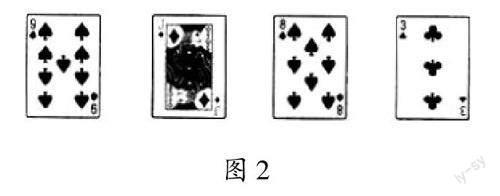
筆者閉上眼，請一名學生將其中1張撲克牌旋轉后放回原位。4張撲克牌的正面如圖2所示。

筆者稍加觀察，便自信地說：“你旋轉了方塊J。”學生紛紛表示太神奇了。結合中心對稱的概念和性質，以及中心對稱圖形的概念，學生明確了：這4張撲克牌中黑桃9、黑桃8和草花3都不是中心對稱圖形，只有方塊J是中心對稱圖形；方塊J旋轉180°后能與原來的圖形重合，其他3張都不行。這樣的游戲互動激發了學生的求知欲，有助于學生養成勤于動手、樂于探究的學習習慣。

責任編輯? 張敏