淺談小學數學課堂練習的優化

葉飛

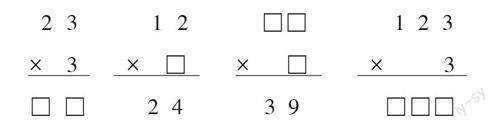
數學練習可以活躍學生思維，鞏固、拓展所學知識。在課堂練習中，教師應積極滲透數學思想方法，促進學生思維能力發展，使其不斷鞏固所學知識。

體現練習的層次性。教師應因材施教，設計不同層次的練習題，使學習水平不同的學生都能獲得發展。學習“兩位數乘一位數的乘法豎式”后，筆者設計了如下一組練習題。

第一道題旨在鞏固基礎知識，是課堂學習的重點內容，相當于第一梯度習題；第二道題是在第一道的基礎上進行的逆向思維訓練，學生需要具備一定的數感，利用“乘數×乘數=積”的關系式進行推算；第三道題在第二道的基礎上更進一步，“39”是一個比較特殊的數，學生需要通過試算，借助所具備的數感，找到有特點的算法“13×3=39”；最后一道題是對兩位數乘一位數算法與算理的拓展，旨在讓學生形成多位數乘一位數的算理和算法的認知。看似簡單的豎式計算體現了練習題之間的梯度，很好地體現了練習設計的層次性。

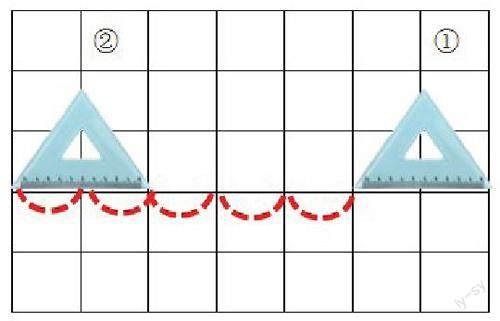
提高練習的針對性。練習課應避免用大量時間訓練學生已經學會的知識。教師應根據教學目標、重難點，以及已有的相關實證研究結果，預設學生的易錯點，并據此設計練習題。學習“平移”的相關知識后，筆者出示下圖并提問：①號三角尺向左平移（? ）格到達②號三角尺的位置？

一名學生搶答“3格”。筆者按學生的回答動態演示①號三角尺向左平移3格。馬上有學生反駁：不是平移3格，應該是平移5格。筆者帶領學生一起驗證，通過演示操作，學生明白了看物體具體平移了幾格，不是看兩個物體之間距離幾格，而是要找到兩個物體的對應點，數對應點之間的格子數。筆者通過制造沖突讓學生深度思考，鞏固了平移的知識。

突出練習的探究性。為了讓練習課“活起來”，使學生在輕松愉悅的氛圍中自主探究、深化知識，筆者嘗試如下活動形式。教學“能被3整除的數的特征”時，筆者分別出示能被2，5整除的數字卡片，讓學生思考下列兩個問題：①能被2整除的數的特征是什么？②能被5整除的數的特征是什么？學生輕松回答后，筆者提出問題：“能被3整除的數的特征是否也有類似的規律呢？”學生受到前面兩個問題的影響，猜想“個位是3，6，9的數能被3整除”。筆者讓學生試一試，算一算。學生自主探究后，發現13，16，19，23，26，29等并不能被3整除，可見顯然上面的說法不對。這時，筆者出示能被3整除的數字卡片，學生憑借已有的知識，算出這些數都是3的倍數。筆者隨即引導學生聚焦其中的一個數“135”，調換各數位上的數字（153，315，351，513，531），讓學生檢驗調換后的各數還是不是3的倍數。學生經過檢驗，發現它們仍然是3的倍數。后續，學生在筆者的引導下發現：如果一個數各個數位上數字之和能被3整除，那么這個數一定能被3整除。

責任編輯? 張敏