啟發式教學在彈性力學課程中的應用
——以圓環或圓筒受均布壓力為例

朱 倩，王 蘇，張常光

（長安大學，西安 710061）

彈性力學是工程力學學科中最基礎、最重要的一門課程，以理論力學、材料力學、結構力學和高等數學為前期課程，后續課程包括塑性力學、斷裂力學、巖石力學、振動理論和有限單元法等，在力學理論體系中具有“承上啟下”的作用[1]。彈性力學兼備了數學、科學和工程三重屬性，將工程問題轉變成嚴密的數學理論體系，成為數學與廣泛工程連接橋梁的一門學科，在土木、水利、機械、交通和航空等工程學科中占有重要的地位[2]。比如，土建工程中，技術人員往往直接利用彈性力學方法作為設計的理論基礎；地震學中，根據彈性波在地殼中傳播的研究結果，計算震源所在的位置并研究地震波傳播的規律。彈性力學課程特點是理論性強、邏輯嚴謹、直觀性差、概念抽象和難理解，并且基本公式推導復雜、求解過程涉及大量的數學偏微分知識[3-4]。學生普遍反映內容枯燥，缺乏興趣，教學也往往難以實現理想效果。因此，如何激發廣大學生的學習興趣，擺脫復雜繁瑣的公式推導所帶來的教學困難，使學生加深對彈性力學在工程應用領域中重要性的認識，建立學生易于接受的教學模式是值得探討和思考的問題。

啟發式教學是當今教改中大力提倡的一種教學模式，目的是使學生真正融入課堂，提高學習興趣和動力，引導學生獨立思考，促使學生積極參與教學活動，針對不同專業人才培養方案的實際需求對教學內容取舍與優化，是提高教學質量與效率的重要探索方法之一[5-6]。彈性力學教學應逐步從單一的課堂教學向多種形式的專業能力培養過渡，理論教學緊密結合實踐案例，幫助學生深入思考，學以致用[7]。將啟發式教學引入彈性力學課堂，打破傳統教學中教師“一言堂”、學生被動輸入知識的課堂模式，讓學生擁有一種“能聽懂、可學會、易掌握、擅應用”的上課理念。鑒于此，本文以彈性力學中“圓環或圓筒受均布壓力”一節為例，綜合多媒體教學手段，采用問題啟發、目的啟發、圖形啟發和案例啟發等靈活多變的教學策略，探索如何融入啟發式教學，增強教學效果。

一 軸對稱應力問題——闡釋生活現象，問題導入，激發興趣

“基于問題的學習”是指將學習設置在有意義的問題情境中，讓學生自主探究，調動學習的主動性[8-9]。針對彈性力學課程抽象困難，采用問題導向法既提高了學生對知識的理解，又激發學生對力學課程的興趣。同時還可與生活現象相結合，將課堂知識與學生日常生活相結合，往往令其印象深刻，產生事半功倍的教學效果。

以老鼠打洞為例[10]，生動形象地闡述動物洞穴涉及的力學問題，可將其簡化為軸對稱力學模型，給出其基本方程、邊界條件，求解其應力變化規律，并指出老鼠打洞對于樁基施工等工程實際問題的啟示及其潛在的工程應用價值，以提高學生的求知欲和學習主動性。再比如講授圓環或圓筒問題時，可融入與生活息息相關的實際問題：有水流經過地面下排水管道的時候，為什么路面上的人卻毫無察覺？以此來引發學生對本節課的理論思考，掌握彈性力基于問題的建模和解析方法。其實，生活中處處皆學問，引導學生熱愛生活，從日常點滴中培養純粹的科研學習熱情。

結合生活現象，引入本節課所需的前置知識，即軸對稱應力問題進行簡明扼要的回顧，使同學們在后續接受本節課的新知識時，能夠迅速與前置知識建立思維關聯。關于平面軸對稱應力問題的一般性解答的公式說明：①按應力求解建立的平面軸對稱應力問題的通解，適用于各種軸對稱應力問題。②軸對稱應力即繞軸應力對稱的條件為物體形狀、面力和體力都是繞軸對稱的。③平面應力、平面應變兩類問題的應力通解相同，只需對E、μ 做簡單變換，即得平面應變問題的位移通解。基于問題啟發，通過闡釋生活現象和對前置知識點的回顧，下面將對本節課后續環節的啟發式教學設計進行探討。

二 圓環或圓筒受均布壓力問題求解——由淺入深，注重教學思路，適時引導

圓環或圓筒受均布壓力問題是彈性力學的經典問題之一，又稱拉梅問題。該問題的求解，應著重教學思路的邏輯性和條理性，淡化數學運算，由淺入深、循序漸進地講解。采用引導與提問相結合的教學方式，逐步帶動學生思維；善于設疑，激發學生的探究欲望。

近年來，祖國飛速發展，修路架橋成就非凡，以海底懸浮隧道為例（圖1），是否能用彈性力學中圓環或圓筒受均布壓力的問題解決該工程結構的受力分析，從而培養學生從實際問題中抽象出力學模型的能力。

圖1 海底懸浮隧道工程實例

（一）應力通解的偉大

圓環（平面應力問題）和圓筒（平面應變問題）受內外均布壓力，屬于軸對稱應力問題，可以引用軸對稱應力問題的通解。顯然海底隧道這一工程結構屬于平面應力問題，但不管是圓環還是圓筒，我們截取單位長度，橫截面都是圓環形，力學模型如圖2 所示。應力通解表達式如下[1]

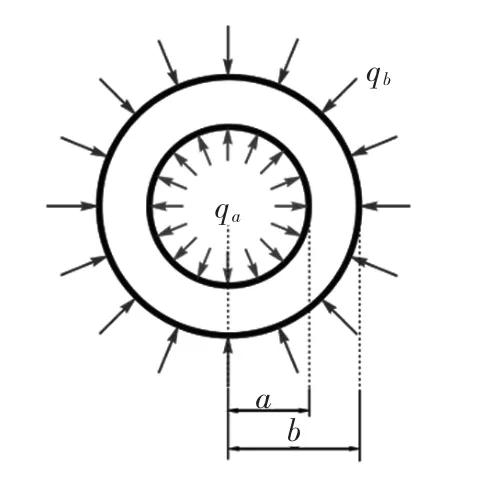
圖2 力學模型

其實通解都是非常偉大的，只要是這一類問題都可以寫成這個形式，可用于求解各種有重要意義的彈性力學具體問題及構造新的通解（比如拉梅解答）。因此，求解平面問題，通解將是最重要的工具[11]。

（二）列寫應力邊界條件

基于應力通解，引導學生思考：如何確定具體問題的解答呢？針對圓環或圓筒這類具體的問題，只不過待定系數不同。彈性力學問題實際上是偏微分方程的邊值問題，邊界條件對確定具體問題的解答起著至關重要的作用。錯誤的邊界條件會導致錯誤的解答，給工程問題留下隱患。因此，邊界條件的識別、書寫及正確運用是基本功。從問題的已知條件分析，屬于應力邊值問題。接下來，我們的任務就是通過列寫應力邊界條件，求出應力通解中的待定系數。特殊邊界采用直接法（或稱比較法）列寫應力邊界條件，那比較法的關鍵問題是什么？標出一點的應力，與邊界上已知的面力作比較。因此，關鍵是要知道坐標系下一點的應力符號規定，圖3 直觀地展示了極坐標系下的應力符號規定。

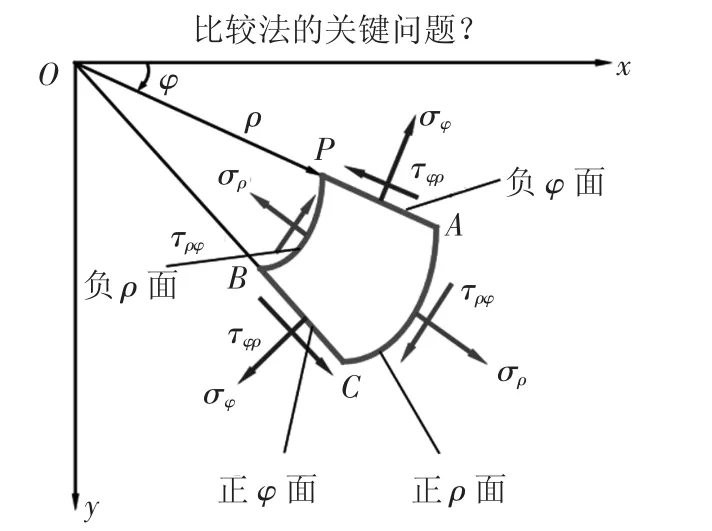
圖3 極坐標下一點的應力符號規定

強調復習助記口訣，面上應力的正方向是以“正面正向為正，負面負向為正”。跟著老師思路寫出本問題的邊界條件

式中有3 個未知量，2 個有效方程，如何求解?

（三）引入位移單值條件

需找補充條件，應力邊界條件已用完，看看位移上有沒有其他條件？轉換思路，從問題本身出發，充分挖掘隱藏的條件：該問題橫截面形狀是一個環形，有兩個連續邊界，而且不相交，力學上稱為多連體。其有一個限制，就是必須考察位移單值條件。本節也是首次引入位移單值條件。為了更直觀地表達，這里舉例說明，如圖4所示，同一個點M，對應無窮多個坐標。

圖4 位移單值條件舉例說明

平面軸對稱應力問題的環向位移表達式如下[1]

在位移解答中，式（3）第一項是位移多值項。要使uφ單值，必須有B=0。結合式（2），即得圓環或圓筒受均布壓力的拉梅解答（應力）

（四）位移單值條件補充說明

對于多連體問題，位移須滿足位移單值條件。大家開動腦筋，這里有什么疑問嗎？①多連體需要，那單連體有單值要求嗎？②只提了位移單值，那應力、應變呢？③位移單值什么意思？是必要的，還是可有可無的？其實這些問題有著深刻的力學意義：多連體位移單值條件實質上是物體連續性假設的表現形式之一，即位移連續性條件；在連續體上，對于同一點的應力、應變或位移都應為單值。

三類力學響應量，都是一個位置一個值。為什么不討論呢？其實這和求解方法有關。①按位移求解時，設/求位移未知函數（單值）；由位移求應變（幾何方程求導）也為單值；由應變求應力（物理方程-代數方程）也為單值；②按應力求解時，設/求應力未知函數（單值）；由應力求應變（物理方程-代數方程）也為單值；由應變求位移（幾何方程積分），常常會出現多值項。

給學生強調一下，按應力求解，也不是所有問題都要考慮位移單值。

三 對拉梅解答的討論——抽象知識具體化，思維拓展，啟發探索

大學生長于形象思維，而不喜抽象思維。教師可將抽象知識具體化，通過討論式教學[12-13]，開拓學生思維，激發學生主動探究的積極性。圓環或圓筒受均布壓力問題（即拉梅問題）是軸對稱應力問題的一個特例，而拉梅解答本身還有幾種更特殊的情況。接下來，分五種情況一一討論，如圖5 所示。

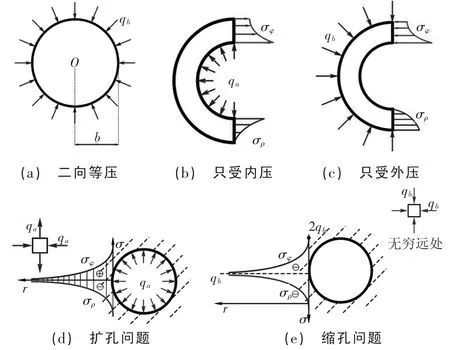
圖5 拉梅解答的討論

其中特別指出：第四種情況，若qa≠0，qb=0，b→∞，即具有圓孔的無限大薄板或彈性體孔壁處受內壓作用，對應靜壓沉樁、頂管及注漿加固等擴孔問題。圖5（d）中可看出，驗證了圣維南原理：在r＞＞a 處，應力很小，即在內壓qa作用下，對b→∞處影響可不計。與前面引出的事例呼應，解釋了“水流經過地下排水管道的時候，為什么路面上的人卻毫無察覺”的生活現象；第五種情況，若qa=0，qb≠0，b→∞，即具有圓形孔道的無限大彈性體無窮遠處受外壓作用，對應隧道開挖、豎井施工及巷道掘進等縮孔問題。由圖5（d）可知，內邊界r=a 處環向應力出現應力集中。通過可視化圖形，啟迪學生對“孔邊應力集中”知識點思考。

四 工程應用舉例——結合實例，學以致用，培養創新能力

啟發式教學還需注重理論學習與工程實例的結合[14]。彈性力學授課過程中，不僅要考慮數理邏輯的嚴謹性，還要兼顧其與工程案例的聯系，充分調動和發揮學生的主體性，根據實際問題，層層剖析，建立力學模型，將實際問題最終化為彈性力學問題，為學生今后的職業發展和創新能力的培養奠定堅實的理論基礎，應用舉例如圖6 所示。

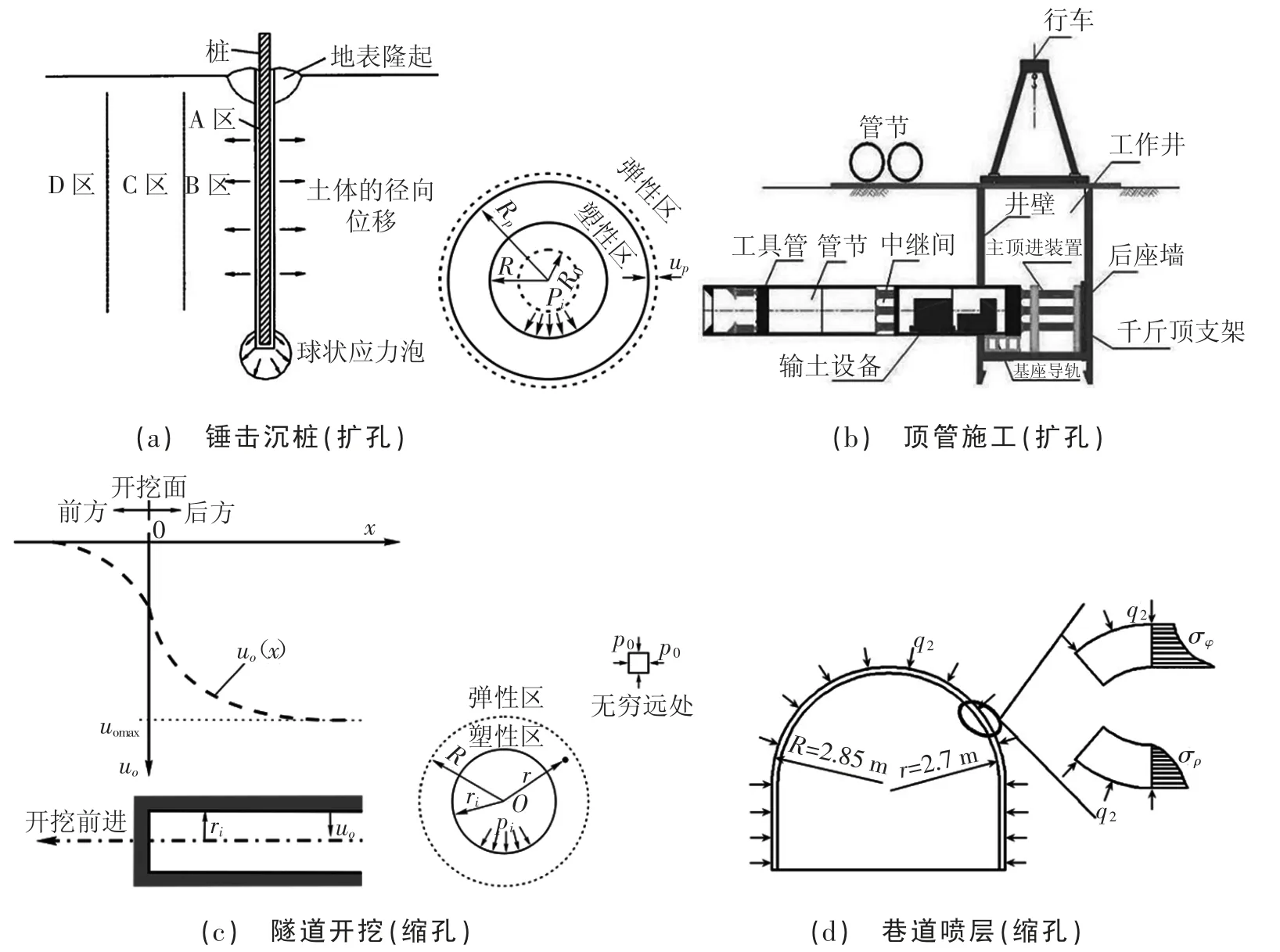
圖6 工程應用實例

將典型的科研案例引入課堂，尋找教學與科研的契合點，讓學生們感受到領悟新知識后的豁然開朗感，激發學生的科研興趣，充分利用已有的知識基礎去解決未知的問題，將未知轉已知，達到真正學以致用的目的。

五 結束語

彈性力學課程具有很強的理論性、抽象性和高度概括性的特點，在本課程的教學實踐中，改變傳統的教學模式，融入啟發式教學法，取得優良的教學效果。本文從以下幾個方面著手實施：①闡釋生活現象，引入問題，激發學習興趣；②由淺入深，注重教學思路，啟發和引導學生思考；③抽象知識具體化，開發學生的邏輯思維，展開討論、啟發探索；④注重理論知識與工程實例結合，學以致用，將未知轉化成已知，提高科研創新能力。啟發式教學有助于學生理論結合實際，合理選擇與優化教學內容，幫助學生克服畏難心理和被動接受知識，激勵學生主動思考，形成一種“能聽懂、可學會、易掌握、擅應用”的教學模式。啟發式教學在彈性力學教學改革的初步探討和有益嘗試，對將來學生綜合素質的培養必然形成良好的促進作用，這也是提高教學效果一個行之有效的教學方法。