譜比法反演震源譜拐角頻率的改進研究

夏晨　利學　周卓群　戚承志

摘要： 由于地震波的信噪比，傳播路徑效應，震源機制差異和震源過程等因素的影響，傳統的譜比法反演的拐角頻率結果不精確，離散性大。以譜比法為基礎，引入Bootstrap重采樣法，Kolmogorov－Smirnov檢驗以及譜比趨勢檢驗的篩選方法，對譜比法的反演結果進行精度評定和篩選，提高譜比法反演的拐角頻率精度。將此方法應用于汶川地震余震的拐角頻率、地震輻射能量、輻射效率以及能矩比等震源參數反演，建立拐角頻率與地震矩之間的對應關系，驗證譜比法以及三種篩選方法的可靠性。汶川地震余震震源參數反演結果表明，汶川地震余震的拐角頻率與地震矩對應關系M0∝f-3.295±0.25c存在與自相似關系M0∝f-3c偏離現象。在地震釋放能量方面，存在能矩比隨地震矩增大而增大，以及大地震的輻射效率大于小地震的現象。

關鍵詞： 譜比法; Bootstrap方法; 拐角頻率; 地震矩; 地震輻射能量; 能矩比

中圖分類號： P319文獻標志碼：A 文章編號： 1000－0844（2023）04-0954-09

DOI：10.20000/j.1000－0844.20210903002

Improvement in the inversion of corner frequency of the source spectrum using the spectral ratio method

XIA Chen LI Xue ZHOU Zhuoqun QI Chengzhi1，2，3

Abstract：? Corner frequency is an important dynamic parameter in seismic source physics. Accurate calculation of the corner frequencies is important for obtaining other seismic source parameters and improving the source spectrum model. However， corner frequency inversion results by the traditional spectral ratio method are inaccurate and discrete due to the signal－to－noise ratio of seismic waves， propagation path effects， differences in source mechanisms， and source processes of earthquakes. In this work， we utilized the spectral ratio method to estimate the corner frequency and implemented three tests （Bootstrap resampling method， Kolmogorov－Smirnov test， and spectral ratio trend test） to evaluate the calculated corner frequencies. These three tests can improve the accuracy of the corner frequencies estimated by the spectral ratio method. The spectral ratio method and these three tests were validated by calculating the seismic source parameters of the aftershocks of the Wenchuan earthquake from May 12 to September 12， 2008. We obtained the corner frequency fc， radiation energy ER， radiation efficiency ηR， and energy－moment ratio e of aftershocks with magnitude 3.7-6.5. According to the calculated results， the relationship between the corner frequency and the seismic moment can be expressed as M0∝f-3.295±0.25c， which is not in agreement with the self－similarity law M0∝f-3c. The seismic radiation energy increases with the earthquake magnitude. When the magnitude increases from 3.7 to 6.5， the energy－moment ratio e also increases from 8 × 10-6 to 5 × 10-5， and the radiation efficiency ηR increases from 0.32 to 0.9. If the self－similarity law holds， then the energy－moment ratio e and the radiation efficiency ηR should be constant. The inversion results of source parameters of Wenchuan earthquake aftershocks show that in terms of the energy released by earthquakes， the energy－moment ratio increases with the seismic moment， and the radiation efficiency of large earthquakes is greater than that of small earthquakes.

Keywords： spectral ratio method; Bootstrap method; corner frequency， seismic moment; seismic radiation energy; energy－moment ratio

0 引言

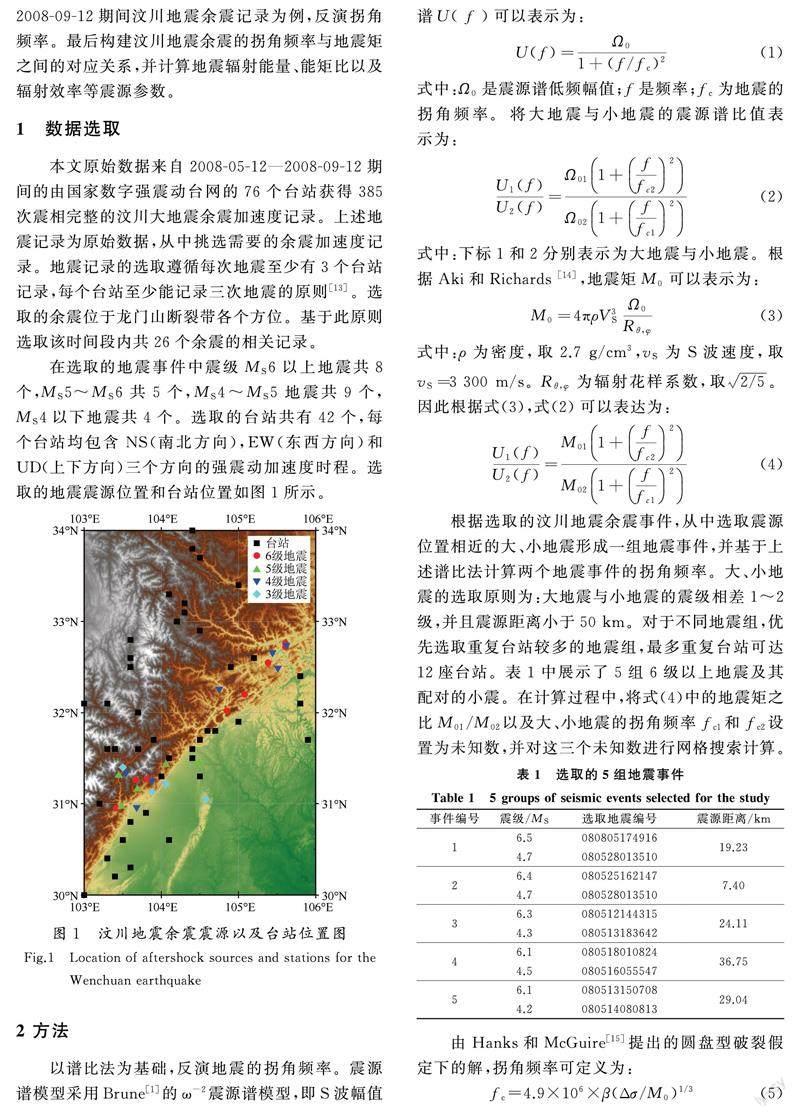
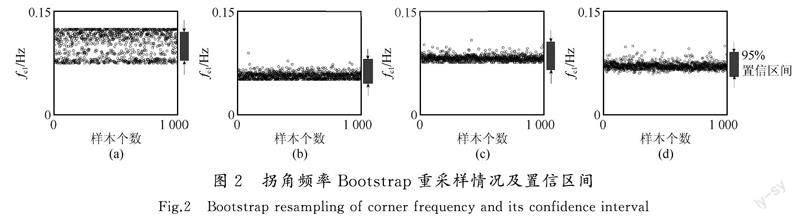
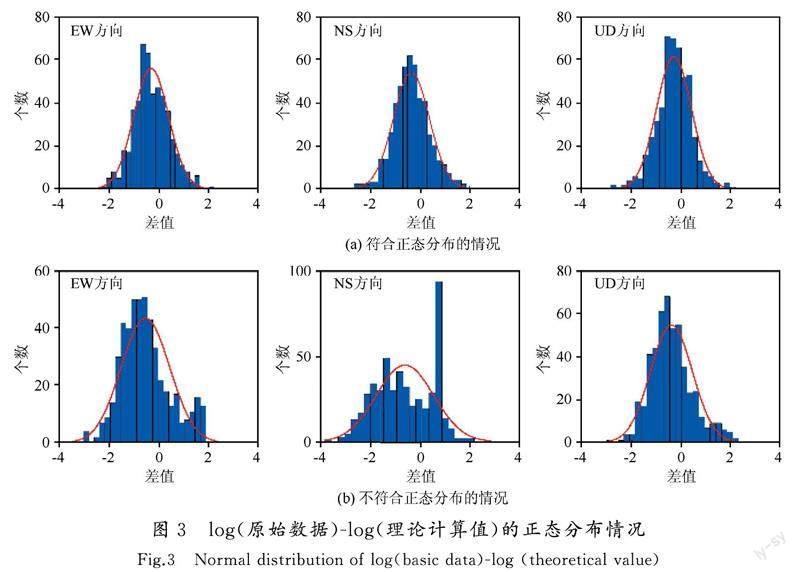
地震震源理論是地震學的重要研究內容。近年來，地震震源研究取得較大進展，根據對臺站記錄的反演求解地震震源參數，也就是所謂的量化地震已經成為地震學研究的重要工作。震源參數對理解震源物理和震源過程具有重要的意義。作為震源物理中重要的參數，拐角頻率直接影響著震源譜模型，因而拐角頻率與其他震源參數之間的關系被眾多學者討論。

在Brune的震源譜模型中，地震遠場位移幅值譜的高頻與低頻漸近線交點處的頻率被定義為拐角頻率［1］。拐角頻率的精確反演，對求解震源參數與完善震源譜模型有著重要的意義。朱新運等［2］使用地震位移譜反演拐角頻率，發現地震的拐角頻率隨地震序列的變化特征可能與區域的應力場有關。Izutani［3］使用譜比法反演拐角頻率，并得到拐角頻率與地震矩之間的關系為M0∝f-3.3±0.2c。楊志高和張曉東［4］通過對首都圈地區117個2.5

譜比法最先由Bath［5］提出，用于計算地層介質的品質因子。其基本思想是：選取兩個標準的地震記錄，將時間域上的地震記錄進行傅里葉轉換到頻率域計算地震的振幅比，通過幅值譜的比值計算震源參數。Ide等［6］指出與頻率無關的品質因子會出現人為的尺寸依賴性，從而導致譜比法計算的地震參數結果不精確。Imanishi等［7］提出并驗證了一種穩定的譜比法，并使用修正經驗格林函數法（MEGF）計算拐角頻率與地震矩。譜比法的優點是應用廣，計算穩定性好，可以避免數值方法難以消除的場地效應和傳播路徑效應的影響。但其缺點也較為明顯，需要依賴的因素較多，地震波形截取長短，地震震級大小以及臺站所記錄到的地震數據都會對譜比法的計算結果產生影響 ［8］。在統計學中Bootstrap重采樣法（自助法）用于偏差分析與方差的統計推斷。Bootstrap重采樣法由Efron ［9］提出之后，已經有部分學者將其運用到地球物理學的研究。Weber［10］利用自助抽樣法對震源參數進行誤差分析。Cesca等［11］通過Bootstrap重采樣對發震斷層位置進行了評估。王樂洋等［12］以Amatrice與Visso地震試驗驗證了Bootstrap重采樣法用于震源參數精度評定的有效性和可靠性。

為了提高拐角頻率的反演精度，本文以譜比法為基礎，引入統計學中的Bootstrap重采樣法（自助法）、Kolmogorov－Smirnov檢驗以及譜比趨勢檢驗對譜比法反演的結果進行篩選。以2008－05－12—2008－09－12期間汶川地震余震記錄為例，反演拐角頻率。最后構建汶川地震余震的拐角頻率與地震矩之間的對應關系，并計算地震輻射能量、能矩比以及輻射效率等震源參數。

1 數據選取

本文原始數據來自2008－05－12—2008－09－12期間的由國家數字強震動臺網的76個臺站獲得385次震相完整的汶川大地震余震加速度記錄。上述地震記錄為原始數據，從中挑選需要的余震加速度記錄。地震記錄的選取遵循每次地震至少有3個臺站記錄，每個臺站至少能記錄三次地震的原則 ［13］。選取的余震位于龍門山斷裂帶各個方位。基于此原則選取該時間段內共26個余震的相關記錄。

在選取的地震事件中震級MS6以上地震共8個，MS5～MS6共5個，MS4～MS5地震共9個，MS4以下地震共4個。選取的臺站共有42個，每個臺站均包含NS（南北方向），EW（東西方向）和UD（上下方向）三個方向的強震動加速度時程。選取的地震震源位置和臺站位置如圖1所示。

2 方法

以譜比法為基礎，反演地震的拐角頻率。震源譜模型采用Brune［1］的ω-2震源譜模型，即S波幅值譜U（ f ）可以表示為：

根據選取的汶川地震余震事件，從中選取震源位置相近的大、小地震形成一組地震事件，并基于上述譜比法計算兩個地震事件的拐角頻率。大、小地震的選取原則為：大地震與小地震的震級相差1～2級，并且震源距離小于50 km。對于不同地震組，優先選取重復臺站較多的地震組，最多重復臺站可達12座臺站。表1中展示了5組6級以上地震及其配對的小震。在計算過程中，將式（4）中的地震矩之比M01/M02以及大、小地震的拐角頻率fc1和fc2設置為未知數，并對這三個未知數進行網格搜索計算。

由Hanks和McGuire［15］提出的圓盤型破裂假定下的解，拐角頻率可定義為：

式中：β為剪切波速，取3 300 m/s，Δσ為應力降。對于fc1與fc2的網格搜索范圍，將式（5）的計算結果fcb設置為理論值，搜索范圍為0.5fcb≤fc≤1.5fcb。對于地震矩之比M01/M02，設置的搜索范圍為1～103。將觀測結果的譜比與理論預測的譜比結果進行對比，在上述搜索范圍里確定最優參數。

由于地震波的信噪比，傳播路徑效應，震源機制差異和震源過程等因素都會影響譜比法的計算結果，造成反演的拐角頻率具有一定的離散性。為降低這些因素的影響，提高譜比法計算結果的可靠性，對譜比法反演的結果引入三種篩選方法——參數的Bootstrap重采樣評定，Kolmogorov－Smirnov正態分布檢驗以及譜比趨勢篩選。保留同時滿足這三個篩選過程的反演結果，剔除不符合任一篩選過程的結果。

2.1 Bootstrap重采樣評定

在統計學中，Bootstrap重采樣法或者叫自助抽樣法是一種從給定訓練集中有放回的均勻抽樣方法，也就是說，每當選中一個樣本，它有可能地被再次選中并被再次添加到訓練集中。自助法由Efron提出，通過重采樣的樣本來描述真實數據的分布情況。當樣本來自總體，能以正態分布來描述，其抽樣分布為正態分布;但當樣本來自的總體無法以正態分布來描述，則以漸進分析法、自助法等來分析。自助法對小數據集的檢測效果好，且自助法可以通過方差的估計構造置信區間，使其運用范圍得到進一步延伸。Bootstrap重采樣法不需要任何的計算模型假設以及精確的計算公式，只需要對樣本的統計量進行檢驗就可以描述真實數據的分布情況以及方差。因此使用Bootstrap重采樣方法可以避免復雜的運算，合理地檢驗計算結果。

在對汶川地震余震拐角頻率的反演中，將理論值fcb代入式（4）得到譜比曲線的理論結果，由網格搜索得到的最佳拐角頻率和地震矩之比代入式（4）得到譜比曲線的反演結果，利用兩者的差值創建一個Bootstrap樣本。利用該樣本對式（4）的理論譜比曲線進行調整，并計算調整后的譜比曲線拐角頻率。為保證反演的精度及計算效率，對每組反演的譜比曲線結果采用1 000次Bootstrap重采樣分析。

為檢驗反演結果是否通過Bootstrap重采樣檢測，對拐角頻率值的Bootstrap取樣設置為95%的置信區間。若取樣結果集中在95%的置信區間之內，則認定此計算結果為合理的，若取樣結果較為分散或者在置信區間之外，將舍棄此計算結果。

圖2（a）與（b）中展示了6.5級與4.7級地震組成的地震組中拐角頻率1 000次Bootstrap取樣情況。（a）為6.5級地震的拐角頻率重新取樣情況，拐角頻率網格搜索區間為0.05～0.15 Hz，由圖中黑色重采樣點可以看出，重采樣情況超出95%的置信區間。而（b）為同一組地震事件中震級為4.7級的地震，搜索區間為0.5～1 Hz，從圖中可以看出重采樣之后反演的拐角頻率值符合95%的置信區間閾值。由于一組地震中大地震的重采樣結果不符合95%的置信區間要求，因此對于此計算結果進行舍棄。圖2（c）與（d）為另一組地震組兩次地震的拐角頻率采樣值，大小地震的重采樣計算均符合95%置信區間的要求，因此該地震組計算結果可取。

2.2 Kolmogorov－Smirnov分布檢驗

理想情況下，理論值及其與實際觀測數據的差值的離散度將遵循正態分布［16］。Kolmogorov－Smirnov檢驗是基于累積分布函數，用以檢驗一個經驗分布是否符合某種理論分布或比較兩種經驗分布是否有顯著差異的方法。本文利用K－S實驗的前一種作用，檢驗log（原始數據）-log（理論計算值）差值的離散度是否符合正態分布。

圖3（a）中展示了符合差值正態分布的結果，其原始數據為6.5/4.7級的地震組事件中LXM臺站所記錄。LXM臺站三個方向的計算結果均符合正態分布，因此該計算結果符合K－S檢測的要求。而圖3（b）中的計算結果不符合K－S實驗中的正態分布，因此剔除該臺站的數據計算得出的拐角頻率結果。

2.3 譜比趨勢的篩選

經過上述兩個步驟的篩選之后，得到同時滿足Bootstrap重采樣和差值正態分布的計算結果。最后一步，將譜比法反演的震源參數帶入式（4），從而得出反演的最佳譜比結果。對比觀測記錄的譜比與反演的最佳譜比結果的曲線重合程度，做最后的篩選。

圖4為經過最終篩選之后得出的兩張圖，圖中紅色曲線為反演的理論值所繪出的曲線，而黑色的曲線為汶川地震余震記錄由傅里葉變換之后得出的結果。圖4（a）中紅色曲線與黑色曲線的趨勢基本相同，因此該臺站的計算結果同時符合上述三個篩選要求。而圖4（b）中紅色曲線與黑色曲線的趨勢相差甚遠，不符合譜比趨勢的要求，此計算結果應剔除。

3 計算與結果分析

運用上述譜比法對所選取的汶川地震余震拐角頻率進行反演，進一步通過三個篩選法則保留符合要求的拐角頻率，計算的震源參數如表2所列。

3.1 拐角頻率與地震矩的對應關系

拐角頻率作為地震譜中高頻與低頻階段漸近線的交點 ，反映了地震震源尺度的大小 ［17］。地震矩是繼地震能量之后的第二個關于震源定量的特征量，也是描述地震大小的絕對力學量。建立拐角頻率與地震矩之間的關系具有重要意義。Kanamori和Anderson以及Hanks在其研究中指出，拐角頻率與地震矩之間的關系遵守地震的自相似法則，即大小地震震源參數之間存在著一定的比例關系，拐角頻率與地震矩的關系式可以表示為［18－19］：

M0∝f_c^-3（6）

由于地震震源的復雜特征，式（6）不完全成立。Aki［20］提出地震存在自相似性偏離現象。使用反演和篩選之后的汶川地震余震拐角頻率值fc，在對數坐標系下對拐角頻率及相應的地震矩進行擬合，得到二者的對應關系。

由式（5）的計算結果可以得到不同震級地震對應的拐角頻率理論值。選取汶川地震余震記錄，其中最小震級為3.7級，由譜比法反演得出對應的拐角頻率為2.52 Hz，最大震級為6.5級，對應的拐角頻率為0.107 Hz。將譜比法反演的拐角頻率結果與Hanks和McGuire［15］的理論值進行對比，結果如圖5所示。圖5中黑色的點為經過譜比法反演所得到的結果，紅色的點為拐角頻率的理論值。結果顯示，使用譜比法反演的拐角頻率結果在小震級時比理論值小，而在大震級時比理論值大。在圖（5）中，對數坐標系下理論值的分布成直線型，直線斜率為-3，對應地震自相似條件下的M0∝f-3c。將譜比法反演得到的拐角頻率在對數坐標系下進行擬合得到黑色實線，黑色實線的斜率為-3.295，擬合區間為（-3.523，-3.06），對應本文所得到的地震矩與拐角頻率的關系式，如式（7）所示。由譜比法反演結果擬合的曲線斜率比理論值的曲線斜率小。

M0∝f_c^-3.295±0.25（7）

圖6對比了反演的汶川地震余震拐角頻率值與Izutani和Kanamori及Izutani的拐角頻率反演結果。圖6中黑色方形的點為本文的計算結果，綠色圓形以及紅色三角形的點為Izutani和Kanamori與Izutani的拐角頻率反演結果。 Izutani和Kanamori［21］得到拐角頻率與地震矩的關系式為：

式中：μ為剪切模量;ΔσS為應力降。表2中的計算結果表明，地震事件中隨著震級從3.7增大到6.5時，輻射效率ηR由0.32增大到0.9。而產生的摩擦能EH大部分會以熱能的形式消散。能矩比e以及輻射效率ηR隨著震級逐漸增大，這兩個現象說明在震級增大過程中地震輻射能量ER在地震釋放能量的占比逐漸變大，因此汶川地震余震在地震釋放能量方面，存在能矩比隨地震矩增大而增大，以及大地震輻射效率大于小地震輻射效率的現象。表明大地震相對于小地震而言是更有效率的地震能量輻射體，地震自相似性偏離現象仍然存在。

4 結論

本文以譜比法為基礎，引入三種篩選方法—Bootstrap重采樣方法，Kolmogorov－Smirnov檢測以及譜比趨勢篩選試驗。避免地震波的信噪比，傳播路徑效應，震源機制差異和震源過程等因素對拐角頻率的反演結果造成影響，提高拐角頻率的反演精度。將此方法運用到對2008－05－12—2008－09－12期間汶川地震余震觀測記錄的震源參數反演，得出3.7～6.5級地震的拐角頻率fc，地震波輻射能ER，輻射效率ηR以及能矩比e等震源參數，并討論參數之間的關系。

根據上述方法反演得出拐角頻率與地震矩的關系可以表示為M0∝f-3.295±0.25c。地震輻射的能量隨著地震震級的增大而增大。當震級從3.7增大到6.5時，能矩比e由8×10-6增大到5×10-5;輻射效率ηR由0.32增大到0.9。反演結果表明，汶川地震余震的拐角頻率與地震矩對應關系存在自相似偏離的現象。地震釋放能量方面，能矩比隨地震矩增大而增大，大地震的輻射效率大于小地震輻射效率的現象。

參考文獻（References）

［1］BRUNE J N.Tectonic stress and the spectra of seismic shear waves from earthquakes［J］.Journal of Geophysical Research，1970，75（26）：4997－5009.

［2］朱新運，鐘羽云，張震峰.地震波拐角頻率對地震序列的依賴性研究［J］.西北地震學報，2004，26（2）：131－136.

ZHU Xinyun，ZHONG Yuyun，ZHANG Zhenfeng.Study on seismic wave corner frequency depending on earthquake sequences［J］.Northwestern Seismological Journal，2004，26（2）：131－136.

［3］IZUTANI Y.Radiated energy from the mid Niigata，Japan，earthquake of October 23，2004，and itsaftershocks［J］.Geophysical Research Letters，2005，32（21）：L21313.

［4］楊志高，張曉東.首都圈地區地震視應力的計算及空間分布［J］.地震，2009，29（4）：32－43.

YANG Zhigao，ZHANG Xiaodong.Computation of apparent stress and its spatial distribution in the capital region of China［J］.Earthquake，2009，29（4）：32－43.

［5］BATH M.Spectral analysis in geophysics［M］.Amsterdam：Elsevier Scientific Pub.Co.，1974.

［6］IDE S，BEROZA G C，PREJEAN S G，et al.Apparent break in earthquake scaling due to path and site effects on deep borehole recordings［J］.Journal of Geophysical Research：Solid Earth，2003，108（B5）：1－13.

［7］IMANISHI K，ELLSWORTH W L.Source scaling relationships of microearthquakes at Parkfield，CA，determined using the SAFOD Pilot Hole seismic array［M］//Earthquakes：Radiated Energy and the Physics of Faulting.Washington，D.C.：American Geophysical Union，2006：81－90.

［8］李曄，郭巍，高也，等.3·21響水爆炸的地震學分析及譜比法研究［J］.地震科學進展，2021，51（5）：215－222.

LI Ye，GUO Wei，GAO Ye，et al.Seismic analysis and amplitude－style spectrum ratio study of the 21 March blast at Xiangshui［J］.Progress in Earthquake Sciences，2021，51（5）：215－222.

［9］EFRON B.Bootstrap methods：another look at the jackknife［J］.The Annals of Statistics，1979，7（1）：1－26.

［10］WBER Z.Probabilistic waveform inversion for focal parameters of local earthquakes［J］.Acta Geodaetica et Geophysica Hungarica，2005，40（2）：229－239.

［11］CESCA S，GRIGOLI F，HEIMANN S，et al.The 2013 September－October seismic sequence offshore Spain：a case of seismicity triggered by gas injection？［J］.Geophysical Journal International，2014，198（2）：941－953.

［12］王樂洋，李志強.震源參數反演及精度評定的Bootstrap方法［J］.地球物理學報，2021，64（6）：2001－2016.

WANG Leyang，LI Zhiqiang.Bootstrap method for inversion and precision estimation of earthquake source parameters［J］.Chinese Journal of Geophysics，2021，64（6）：2001－2016.

［13］華衛，陳章立，鄭斯華，等.三峽水庫地區震源參數特征研究［J］.地震地質，2010，32（4）：533－542.

HUA Wei，CHEN Zhangli，ZHENG Sihua，et al.A study on characteristics of source parameters in Three Gorges Reservoir area［J］.Seismology and Geology，2010，32（4）：533－542.

［14］AKI K，RICHARDS P G.Quantitative seismology：theory and methods［M］.San Francisco：W H Freeman，1980.

［15］HANKS T C，MCGUIRE R K.The character of high－frequency strong ground motion［J］.Bulletin of the Seismological Society of America，1981，71（6）：2071－2095.

［16］YOSHIMITSU N，ELLSWORTH W L，BEROZA G C.Robust stress drop estimates of potentially induced earthquakes in Oklahoma：evaluation of empirical green's function［J］.Journal of Geophysical Research：Solid Earth，2019，124（6）：5854－5866.

［17］王鵬，鄭建常，王寶善，等.山東乳山震群震源參數變化及其尺度關系［J］.地球物理學進展，2020，35（6）：2096－2106.

WANG Peng，ZHENG Jianchang，WANG Baoshan，et al.Scale relationship and variation of source parameters of Rushan earthquake swarm［J］.Progress in Geophysics，2020，35（6）：2096－2106.

［18］KANAMORI H，ANDERSON D L.Theoretical basis of some empirical relations in seismology［J］.Bulletin of the Seismological Society of America，1975，（65）：1073－1096.

［19］HANKS T C.Earthquake stress drops，ambient tectonic stresses and stresses that drive plate motions［J］.Pure and Applied Geophysics，1977，115（1）：441－458.

［20］AKI K.A new view of earthquake and volcano precursors［J］.Earth，Planets and Space，2004，56（8）：689－713.

［21］IZUTANI Y，KANAMORI H.Scale－dependence of seismic energy－to－moment ratio for strike－slip earthquakes in Japan［J］.Geophysical Research Letters，2001，28（20）：4007－4010.

［22］KANAMORI H，BRODSKY E E.The physics of earthquakes［J］.Reports on Progress in Physics，2004，67（8）：1429－1496.

［23］KANAMORI H，RIVERA L.Energy partitioning during an earthquake［M］//Earthquakes：Radiated Energy and the Physics of Faulting.Washington，D. C.：American Geophysical Union，2006：3－13.

［24］BEN－MENAHEM A，SINGH S J.Seismic waves and sources［M］.New York：Springer－Verlag，1981.

［25］KANAMORI H，HEATON T H.Microscopic and macroscopic physics of earthquakes［M］//Geocomplexity and the Physics of Earthquakes.Washington，D. C.：American Geophysical Union，2000：147－163.

［26］IDE S，BEROZA G C.Does apparent stress vary with earthquake size？［J］.Geophysical Research Letters，2001，28（17）：3349－3352.

［27］YAMADA T.Radiation efficiency and apparent stress of small earthquakes in a South African gold mine［J］.Journal of Geophysical Research，2005，110（B1）：B01305.

［28］HUSSEINI M I.Energy balance for motion along a fault［J］.Geophysical Journal International，1977，49（3）：699－714.（本文編輯：任 棟）

收稿日期：2021-09-03

基金項目：國家自然科學基金（51708018）;北京市教委科研項目－科技計劃一般項目（KM202010016016）;北京建筑大學市屬高校基本科研業務費專項資金資助（X18268，X19025）

第一作者簡介：夏 晨（1989-），男，博士，副教授，主要研究方向為強地震動模擬，震源物理以及地下結構抗震。

E－mail：xiachen@bucea.edu.cn。