雙組分混紡紗斷裂比功與混紡比的關系

周宇陽, 王旭斌, 曹巧麗, 李 豪, 錢麗莉, 郁崇文,2

(1.東華大學 紡織學院, 上海 201620; 2.東華大學 紡織面料技術教育部重點實驗室, 上海 201620)

如今,紡織品越來越多地作為基礎材料應用到航空航天[1]、交通運輸[2]和建筑[3]等各行各業中,這也要求它具有相應的性能。大部分的紡織品由紗線組成,紗線的拉伸性能對最終產品的性能影響較大。紡織工業中通常將不同的纖維混合,通過紡紗工藝紡制成混紡紗,達到綜合多種纖維優點、提高成紗性能以及降低成本的目的[4]。雙組分混紡紗的紡紗難度較小,技術更為成熟,也是最為常見的混紡品種。為此,研究雙組分混紡紗的拉伸性能具有重要意義。

斷裂強度、斷裂伸長率和斷裂比功等都屬于混紡紗的拉伸性能指標。長期以來,斷裂強度作為最常用的指標,受到了學者們的廣泛關注[5-6],但在實際使用中混紡紗通常是受到反復拉伸或軸向沖擊作用,斷裂強度只能衡量力的大小,在該情況下無法準確地評價混紡紗的抗破壞能力。而斷裂比功是指拉斷單位線密度、單位長度的紗所需要做的功,能夠衡量混紡紗的堅牢度、耐久性[7-8]與抗軸向沖擊性能[9]。例如,在織造生產過程中經紗會受到反復的拉伸作用,強度高但斷裂比功小的麻紗易斷頭;而強度低但斷裂比功大的棉紗斷頭較少。又如強度高但斷裂比功小的環錠紗斷頭較多;而強度較低但斷裂比功大的轉杯紗斷頭就較少。這些都表明紗的斷裂比功能更好地反映紗的抗破壞能力。實際上,它是斷裂強度與斷裂伸長率的綜合體現,可表示為拉伸曲線(強度-伸長率曲線)下方的面積。

混紡紗的斷裂比功與各組分的混紡比關系密切,所以預測斷裂比功隨混紡比變化的規律,在混紡紗的生產加工以及產品應用中至關重要;但是目前相關研究較少,且主要是經驗上的定性分析。1979年, Duckett等[10]通過將純棉紗與純滌綸紗的拉伸曲線簡化為直線,并假設在滌棉混紡紗中二組分之間沒有相互作用,建立了斷裂比功與混紡比的關系式。但該式只有在混紡紗斷裂伸長率已知的條件下才能計算出混紡紗的斷裂比功,所以無法用于斷裂比功的預測。國內一些學者在實驗數據的基礎上探討了混紡紗斷裂比功與混紡比的關系。楊慶斌等[11]發現,在大豆蛋白復合纖維與棉或與滌綸混紡時,斷裂比功隨混紡比變化的趨勢與斷裂強度隨混紡比變化的趨勢相似;于璐等[12]則發現,聚乳酸纖維與Modal纖維混紡時斷裂比功變化趨勢的轉折點與斷裂伸長率的轉折點一致。上述研究都沒有進行深入討論。

為深入探究混紡紗斷裂比功與混紡比的關系,本文從預測混紡紗拉伸曲線的角度出發,在前人對混紡紗斷裂強度、斷裂伸長率研究[13]的基礎上,建立了一個簡單的拉伸曲線模型。通過推算曲線下方的面積,建立雙組分混紡紗斷裂比功與混紡比的關系式;并通過混紡實驗數據,驗證該關系式的適用性與可靠性。

1 混紡紗斷裂強度與斷裂伸長率分析

雙組分纖維混紡時,定義純紡紗斷裂伸長率較小的組分為A組分,伸長率較大的為B組分。假設:A組分純紡紗的斷裂強度為SA,斷裂伸長率為εA;B組分純紡紗的斷裂強度為SB,當伸長率為εA時對應的強度為S′B,斷裂伸長率為εB。A組分在混紡紗中的含量(即混紡比)為a,B組分在混紡紗中的含量(即混紡比)為b=1-a。A組分和B組分的純紡紗拉伸曲線如圖1所示。

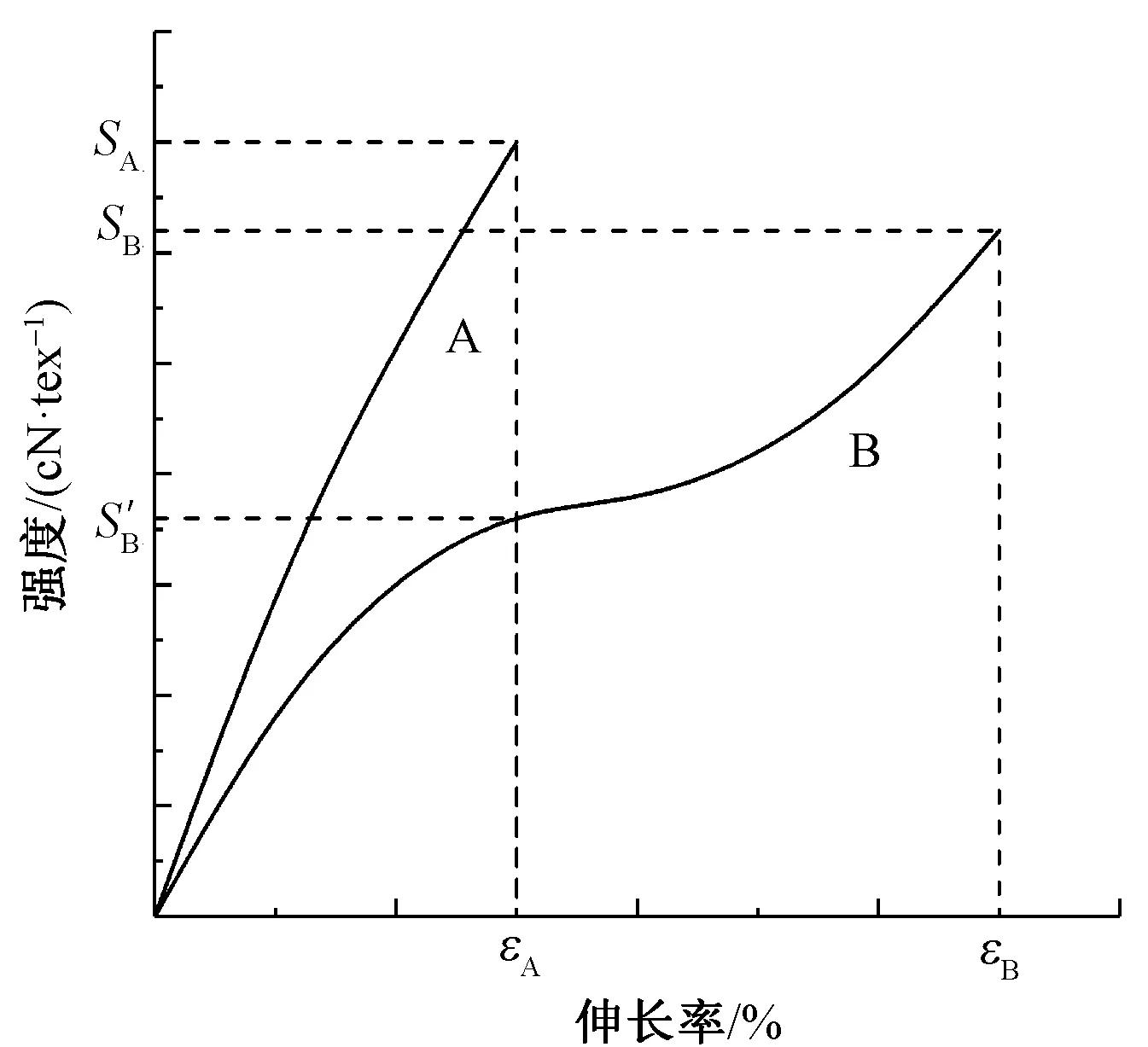
圖1 A組分純紡紗與B組分純紡紗的拉伸曲線Fig.1 Tensile curves of 100% A yarn and 100% B yarn

1.1 混紡紗斷裂強度

1975年,Gupta等[14]發現,將Hamburger提出的混紡紗強度公式[5]中纖維的強伸性能轉換成其純紡紗的強伸性能,預測結果與實測值會有較好的吻合度。郁崇文等[13]的研究也進一步證實了這一點。斷裂強度S的表達式如下:

S=max{S1,S2}

(1)

其中

S1=aSA+bS′B

(2)

S2=bSB

(3)

圖2中的實線即混紡紗斷裂強度隨混紡比變化的曲線。當S1=S2時,對應的B組分含量稱為臨界混紡比bC,通過式(2)、(3)可推導出bC的計算式:

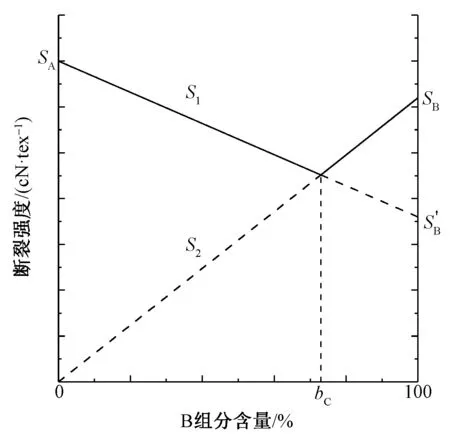
圖2 混紡紗斷裂強度與混紡比的關系Fig.2 Relationship between bended ratio and tenacity of blended yarn

(4)

1.2 混紡紗斷裂伸長率

通過對混紡紗斷裂過程的分析以及對斷裂伸長率經驗數據的總結,郁崇文等[13]發現斷裂伸長率隨混紡比變化的趨勢基本呈現圖3所示的規律,于是提出了混紡紗斷裂伸長率ε的表達式:

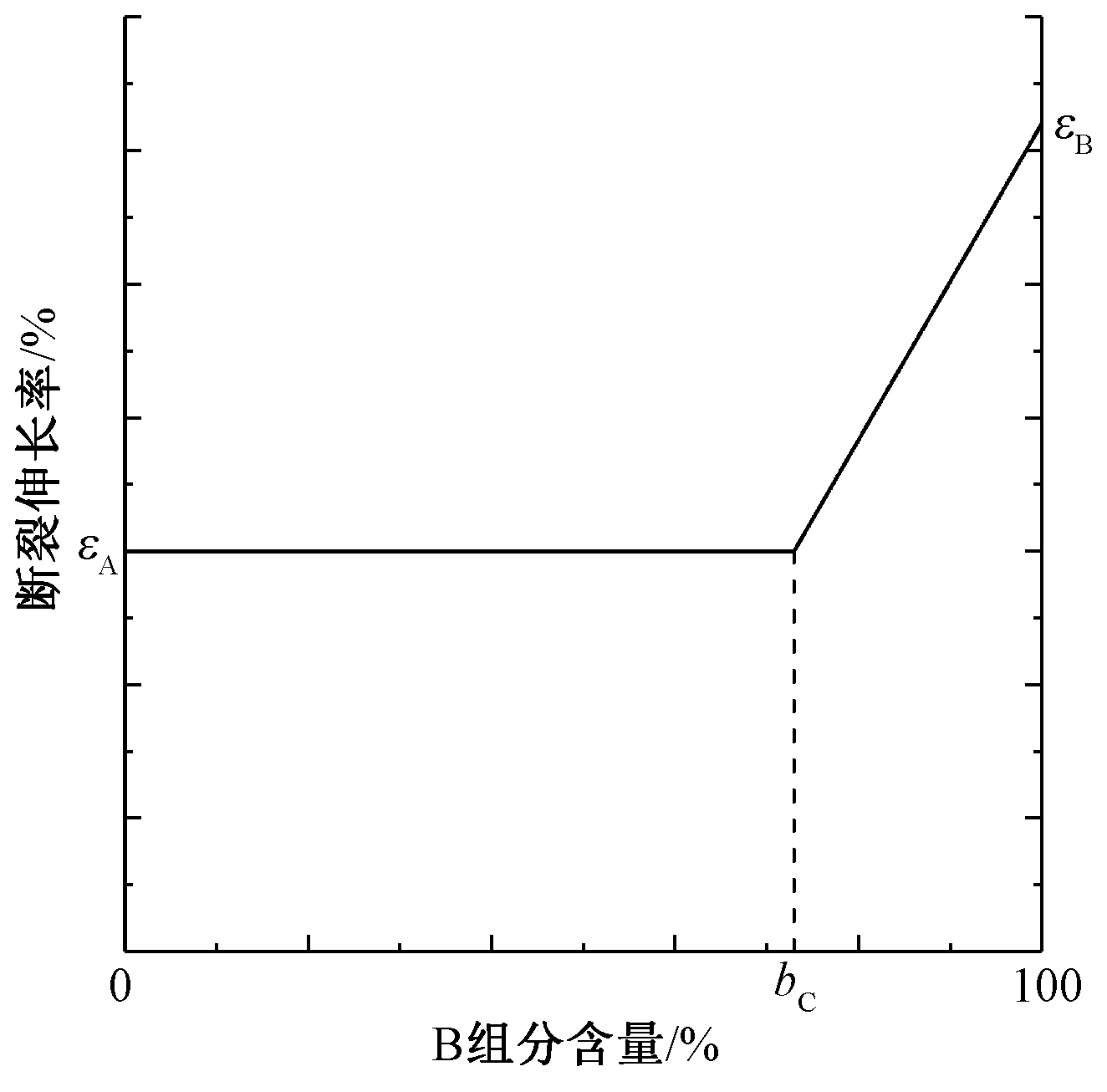
圖3 混紡紗斷裂伸長率與混紡比的關系Fig.3 Relationship between blended ratio and breaking extension of blended yarn

(5)

2 混紡紗斷裂比功分析

混紡紗斷裂比功在數值上等于其拉伸曲線(強度-伸長率曲線)下方的面積,因此,預測出混紡紗的拉伸曲線,就能夠推算出其斷裂比功。通過式(1)～(5)可預測出混紡紗拉伸曲線上部分點的坐標。將這些點以及坐標原點用直線連接,就得到簡化的拉伸曲線,進而可推導出拉伸曲線下方圖形面積(即斷裂比功)的表達式。通過文獻[13]對混紡紗斷裂過程的分析可以發現,以臨界混紡比bC為界,可將混紡紗的斷裂過程分為2種,不同的斷裂過程對應著不同的表達式。

2.1 混紡比b小于或等于bC

混紡紗受到拉伸作用時,在初始階段A、B二組分共同承受外力。當伸長率達到εA時,混紡紗的強度為S1。如果繼續拉伸,A組分將斷裂,所有的外力主要由B組分承受。此時,由于B組分含量較小(b≤bC), 其承載極限S2小于S1,所以整個紗體斷裂。S1與εA就是混紡紗的斷裂強度和斷裂伸長率。將混紡紗拉伸曲線簡化為拉伸起始點O(0,0)與紗體斷裂點P(εA,S1)的連線OP,則線段OP下方三角形的面積即為斷裂比功W,如圖4所示。其中灰色斜紋部分的面積即預測斷裂比功:

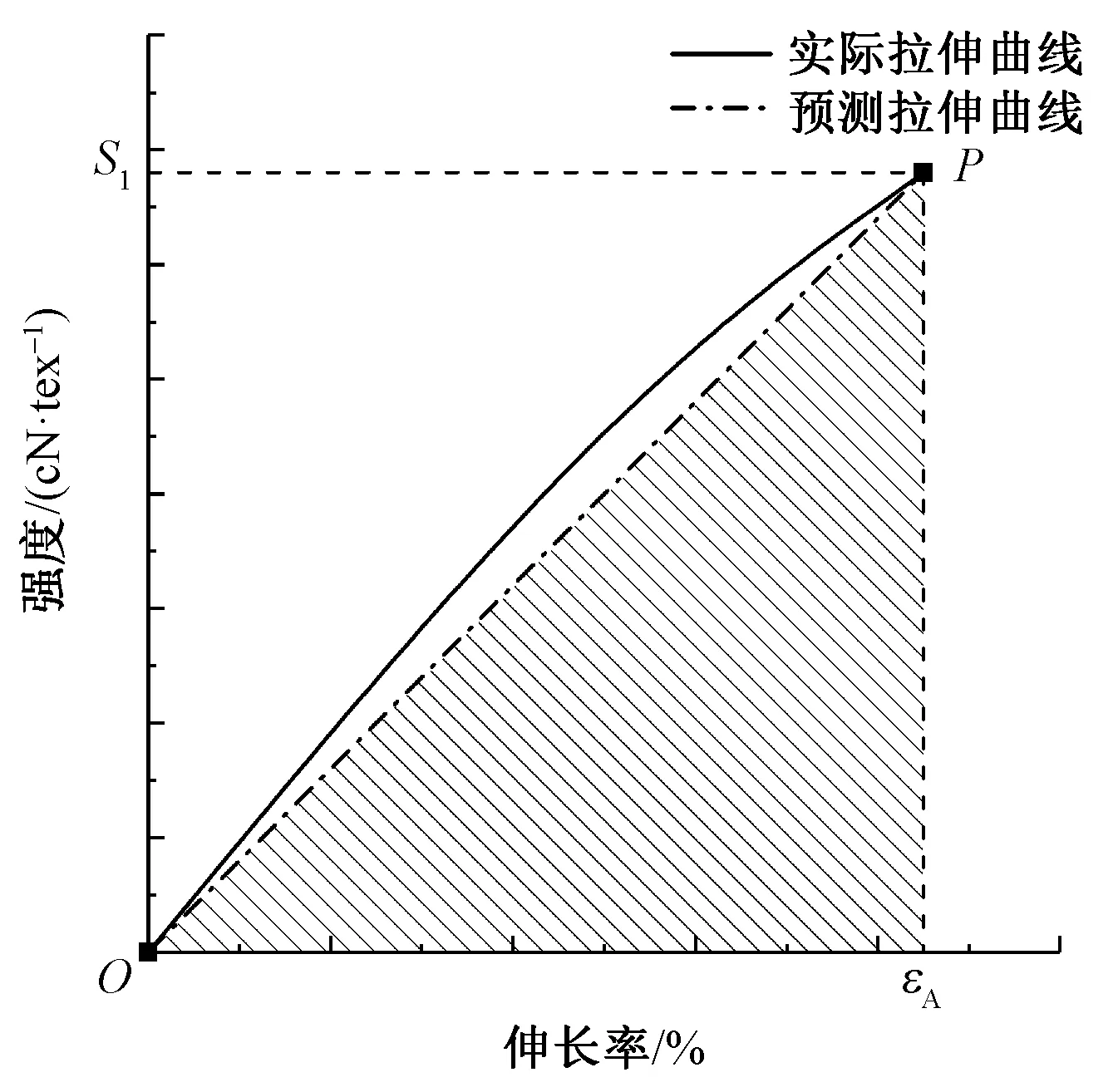
圖4 混紡紗實際與預測拉伸曲線(b≤bC)Fig.4 Practical and predicted tensile curve of blended yarn (b≤bC)

(6)

2.2 混紡比b大于bC

隨著B組分含量的增大,其承載極限S2也逐漸增大。當B組分含量超過臨界值bC時,S1小于S2,所以A組分斷裂后,B組分仍能夠單獨承受拉伸,繼續伸長,直到伸長率為ε時B組分也斷裂,即整個紗體斷裂。S2與ε即為混紡紗的斷裂強度與斷裂伸長率。可將混紡紗拉伸曲線簡化為:拉伸起始點O(0,0)、A組分斷裂點P(εA,S1)和紗體斷裂點M(ε,S2)的連線OPM,折線OPM下方圖形(即三角形加梯形)的面積則為斷裂比功W,如圖5所示。圖5(a)、 (b)分別為2種典型的混紡紗拉伸曲線示意圖。灰色斜紋部分的面積即為預測斷裂比功:

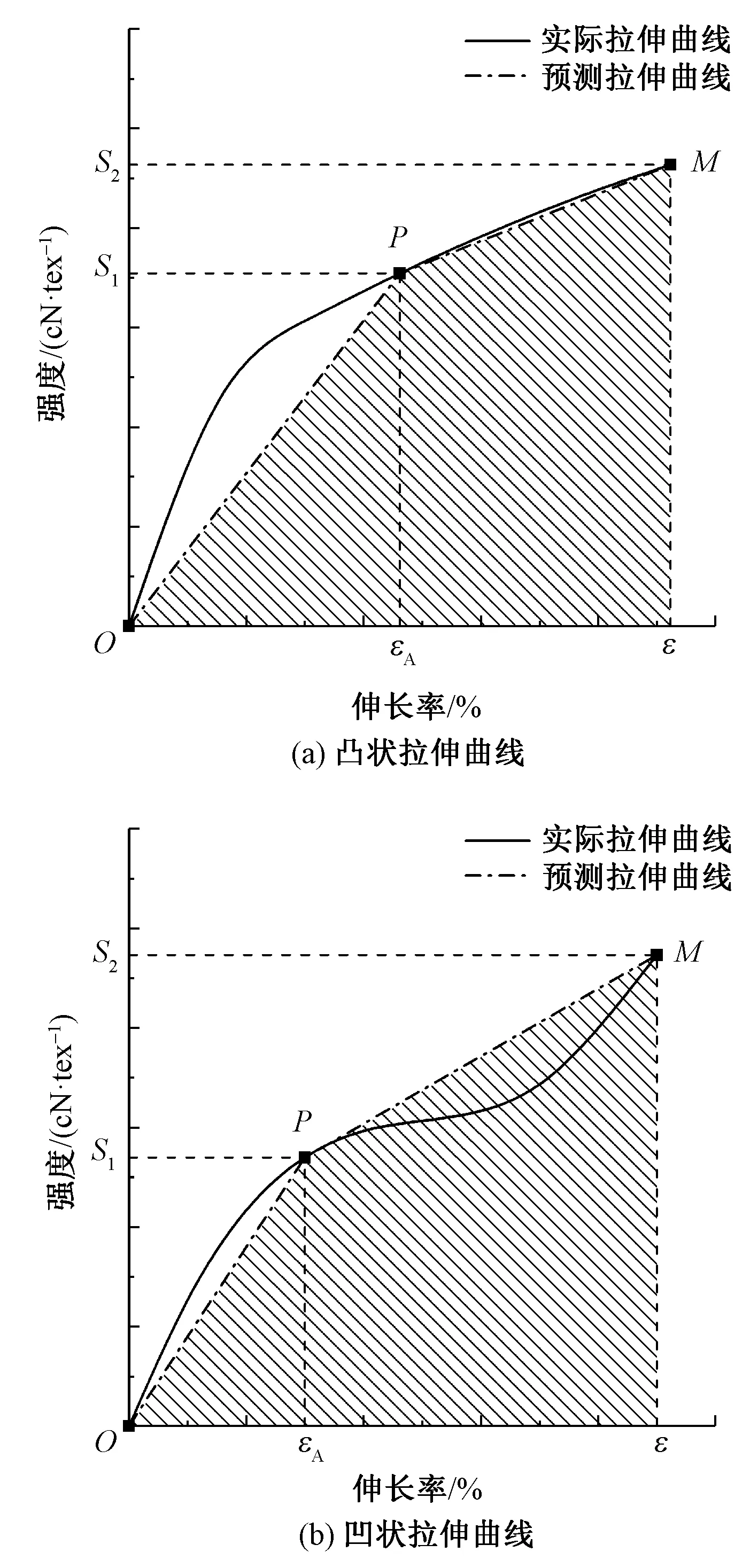
圖5 混紡紗實際與預測拉伸曲線(b>bC)Fig.5 Practical and predicted tensile curve of blended yarns (b>bC).(a)Convex curve; (b)Concave curve

(7)

綜上所述,混紡紗斷裂比功與純紡紗拉伸性能、混紡比之間的關系式為

(8)

由式(8)可見,與斷裂強度、斷裂伸長率相似,斷裂比功隨混紡比變化的趨勢在臨界混紡比bC處發生轉變。

3 斷裂比功-混紡比關系式的驗證

3.1 實驗驗證

為驗證上述斷裂比功-混紡比關系式的可靠性,設計了棉與粘膠2種纖維的混紡實驗,紡制了線密度為25 tex、捻系數為355的純棉紗、純粘膠紗和4種棉/粘膠混紡紗(混紡比分別為20∶80、40∶60、60∶40、 80∶20)。使用YG061F型電子單紗強力儀,按照GB/T 3916—2013《紡織品 卷裝紗 單根紗線斷裂強力和斷裂伸長率的測定(CRE法)》測試了成紗的拉伸性能。純紡紗的拉伸曲線如圖6所示,可以得到純紡紗拉伸性能:SA=13.68 cN/tex,SB=9.71 cN/tex,S′B=8.90 cN/tex,εA=6.93%,εB=7.90%(A組分為棉,B組分為粘膠)。

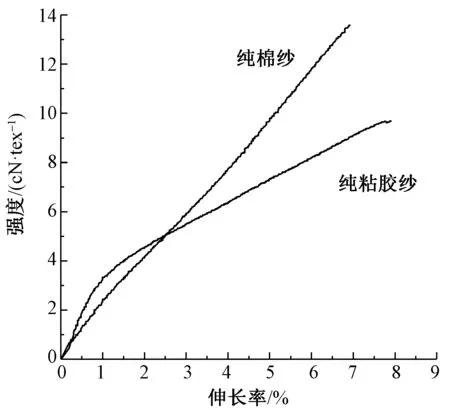
圖6 純棉紗與純粘膠紗拉伸曲線Fig.6 Tensile curves of cotton yarn and viscose yarn

根據式(1)～(8)計算出不同混紡比下混紡紗的拉伸性能,并與實測值進行對比,結果如圖7所示。計算得出臨界混紡比bC為94%。通過圖7(a)可以看出,預測的斷裂比功變化趨勢與實測結果基本相符。

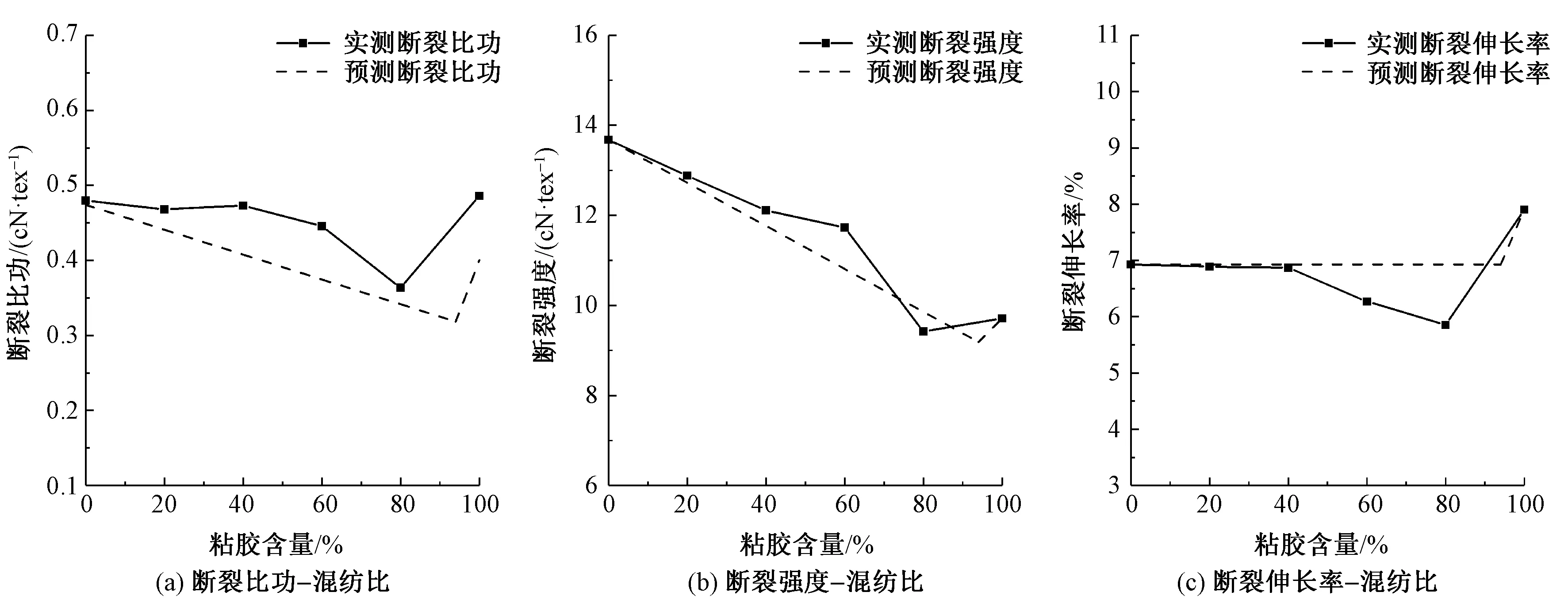
圖7 棉/粘膠纖維混紡紗拉伸性能Fig.7 Tensile properties of cotton/viscose fiber yarn.(a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

本實驗中,斷裂比功隨著粘膠纖維含量的增加,以臨界混紡比bC為界,呈現先減小后增加的趨勢。斷裂比功的實測值總是高于預測值,主要原因是棉/粘膠混紡紗拉伸曲線呈凸狀,而預測拉伸曲線為直線。實際曲線總高于預測曲線,其下方面積大于預測曲線下方面積。例如,當棉與粘膠混紡比為60∶40 時,實測拉伸曲線明顯呈凸狀,致使斷裂比功預測值偏小,如圖8(a)所示。當棉與粘膠混紡比為20∶80時,預測拉伸曲線明顯低于實際凸狀拉伸曲線,導致斷裂比功預測值偏小;同時,斷裂強度、斷裂伸長率預測值偏大,會導致斷裂比功預測值偏大,從而部分抵消了實際拉伸曲線呈凸狀帶來的誤差見圖8(b)。

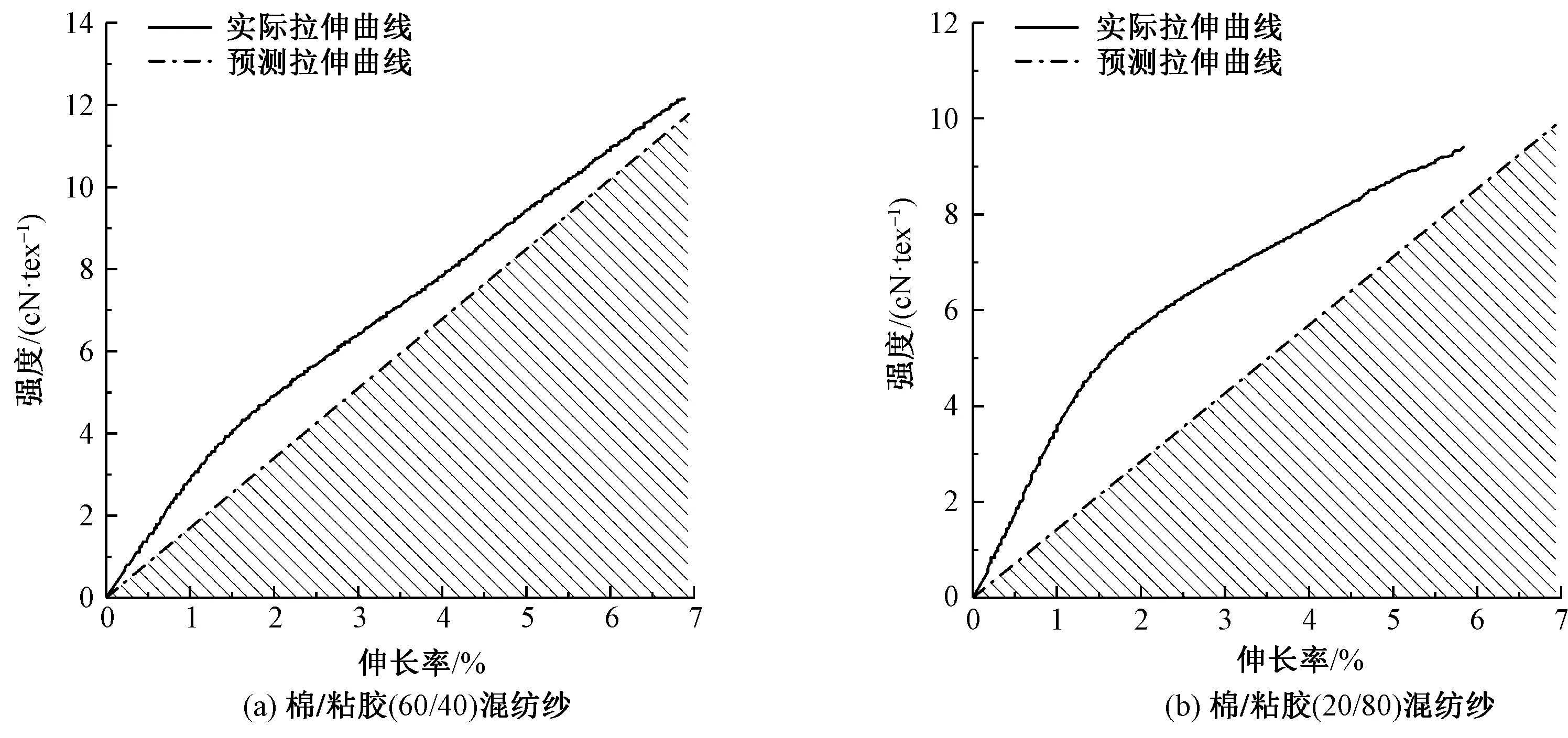
圖8 棉/粘膠混紡紗拉伸曲線Fig.8 Tensile curves of cotton/viscose yarn.(a)cotton/viscose(60/40) yarn; (b)cotton/viscose(20/80) yarn

3.2 文獻案例驗證

為進一步驗證斷裂比功-混紡比關系式的適用性與可靠性,使用文獻中混紡案例的純紡紗拉伸測試數據(見表1)預測混紡紗的拉伸性能隨混紡比變化的情況,并與實測值進行對比,如圖9～15所示。上述文獻主要討論混紡比與斷裂強度、斷裂伸長率的關系,并未深入討論斷裂比功。部分案例中的原始數據為斷裂功,此處為方便討論,均根據下式換算為斷裂比功:

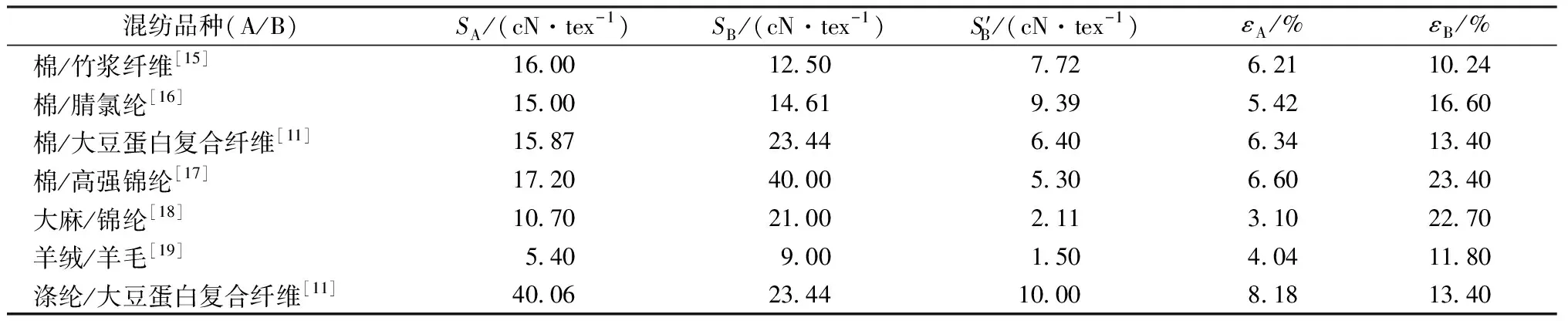
表1 文獻中各種純紡紗的拉伸性能Tab.1 Tensile properties of various pure spun yarns in literatures

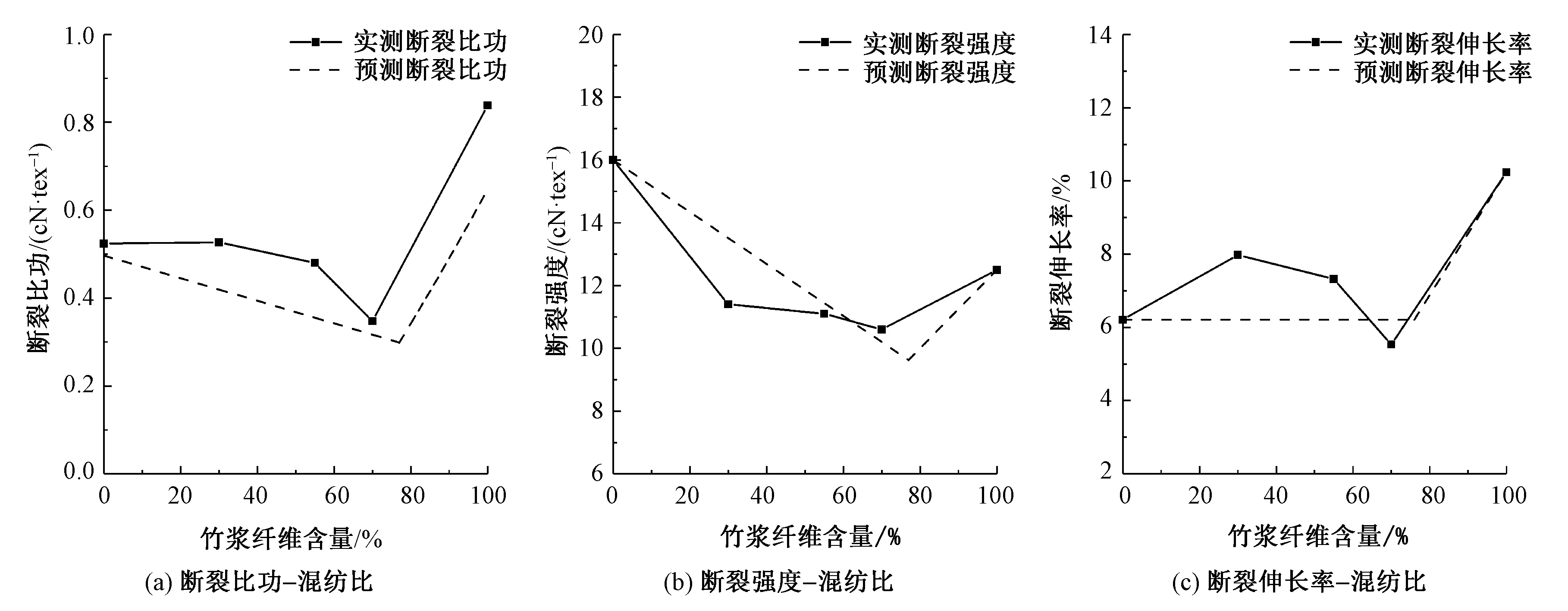
圖9 棉/竹漿纖維混紡紗拉伸性能Fig.9 Tensile properties of cotton/bamboo pulp fiber yarn.(a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

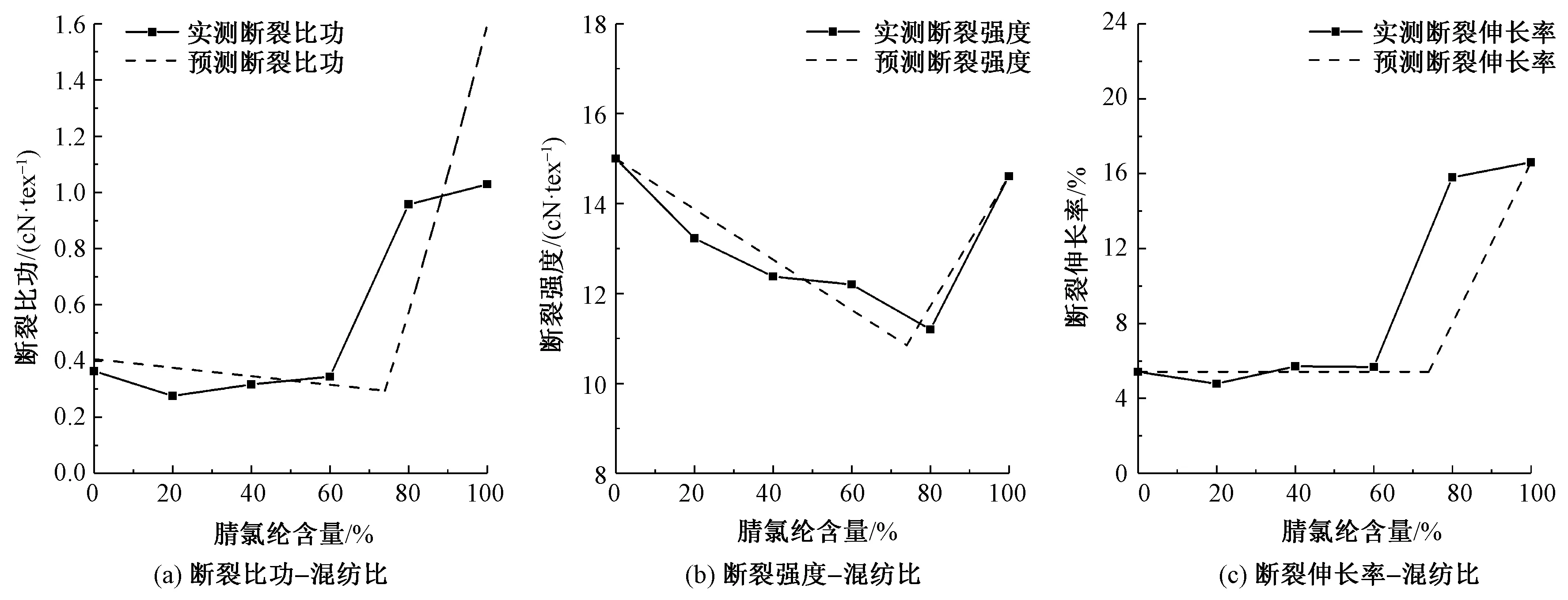
圖10 棉/腈氯綸混紡紗拉伸性能Fig.10 Tensile properties of cotton/modacrylic yarn.(a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

(9)

由圖9～15可看出,與斷裂強度和斷裂伸長率相似,斷裂比功的變化趨勢在臨界混紡比bC附近發生轉變。針對不同種類的混紡紗,斷裂比功預測值隨混紡比變化的趨勢與實測結果基本相符,證明本文提出的關系式具有一定普適性。

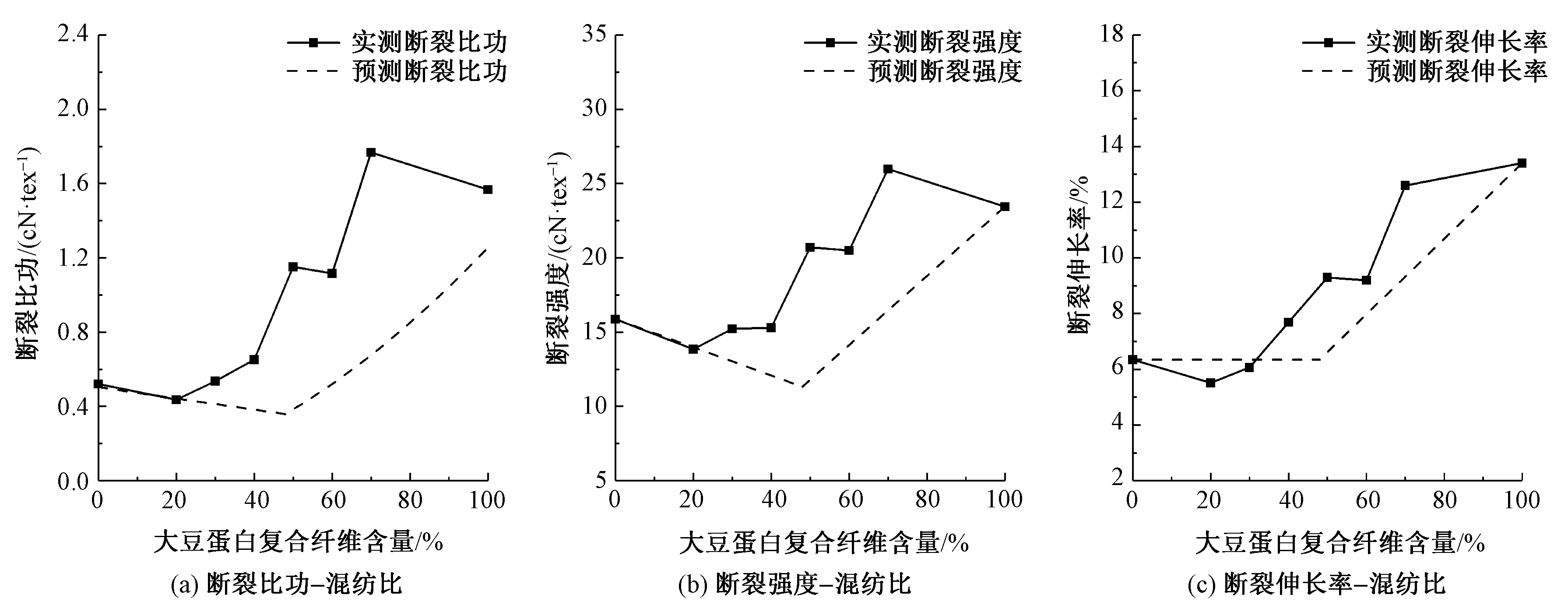
圖11 棉/大豆蛋白復合纖維混紡紗拉伸性能Fig.11 Tensile properties of cotton/soybean protein fiber yarn.(a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

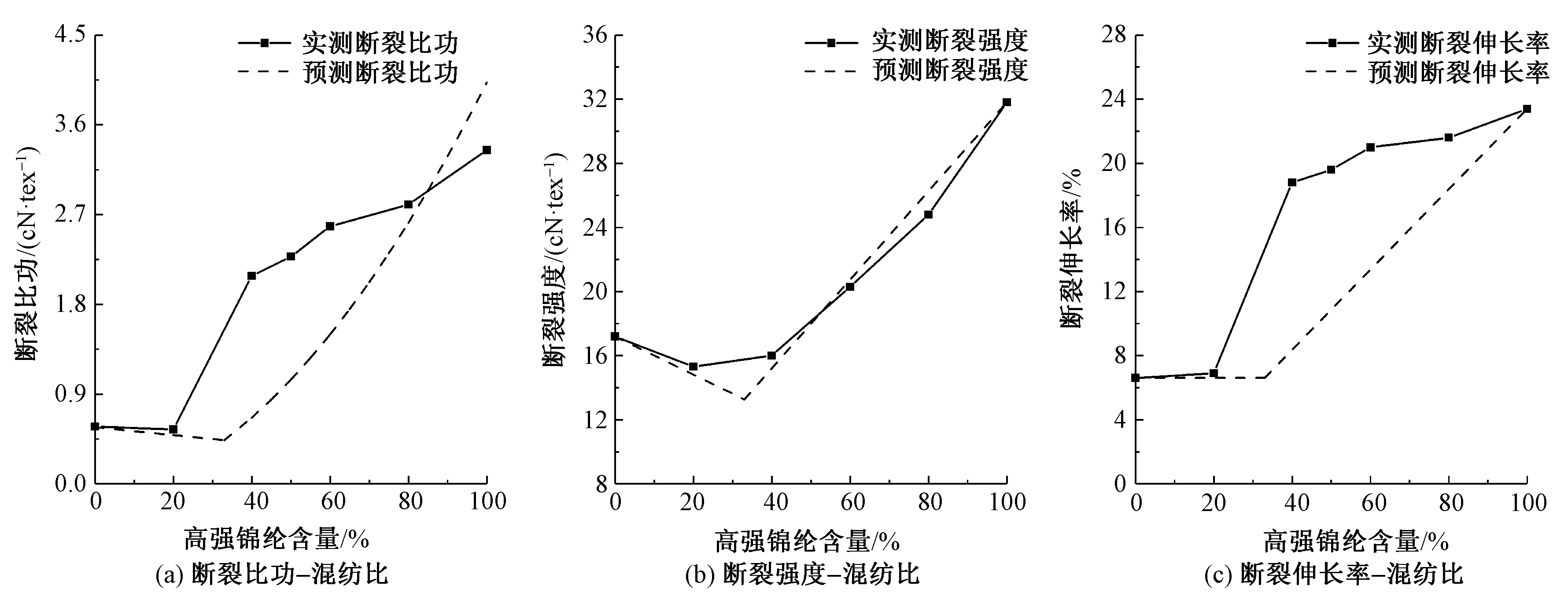
圖12 棉/高強錦綸混紡紗拉伸性能Fig.12 Tensile properties of cotton/high strength polyamide yarn.(a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

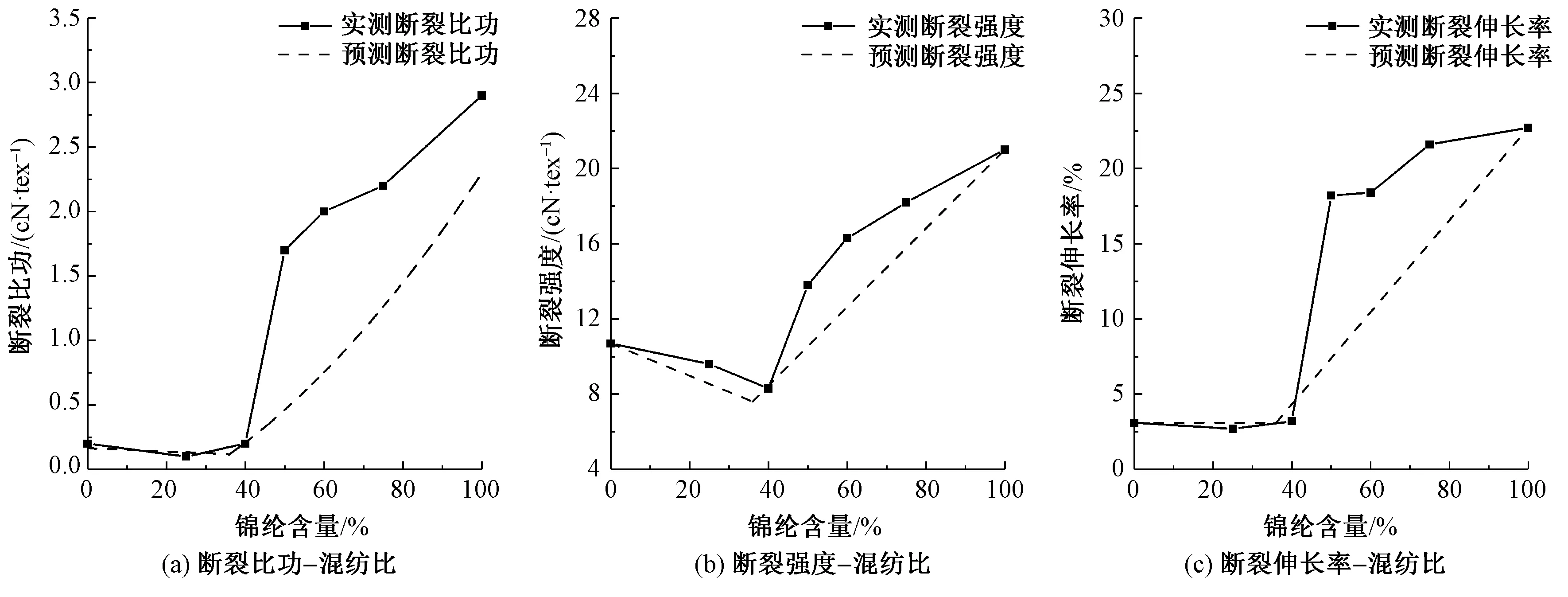
圖13 大麻/錦綸混紡紗拉伸性能Fig.13 Tensile properties of hemp/polyamide yarn. (a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

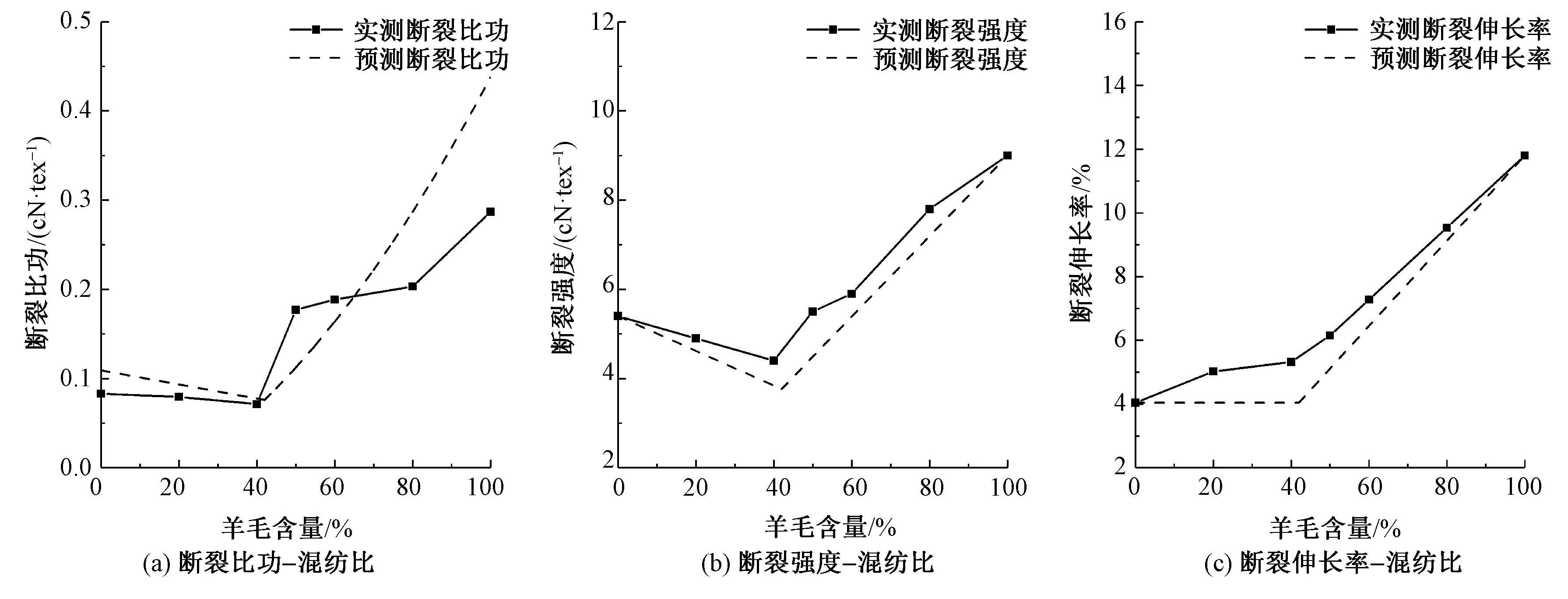
圖14 羊絨/羊毛混紡紗拉伸性能Fig.14 Tensile properties of cashmere/wool yarn.(a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

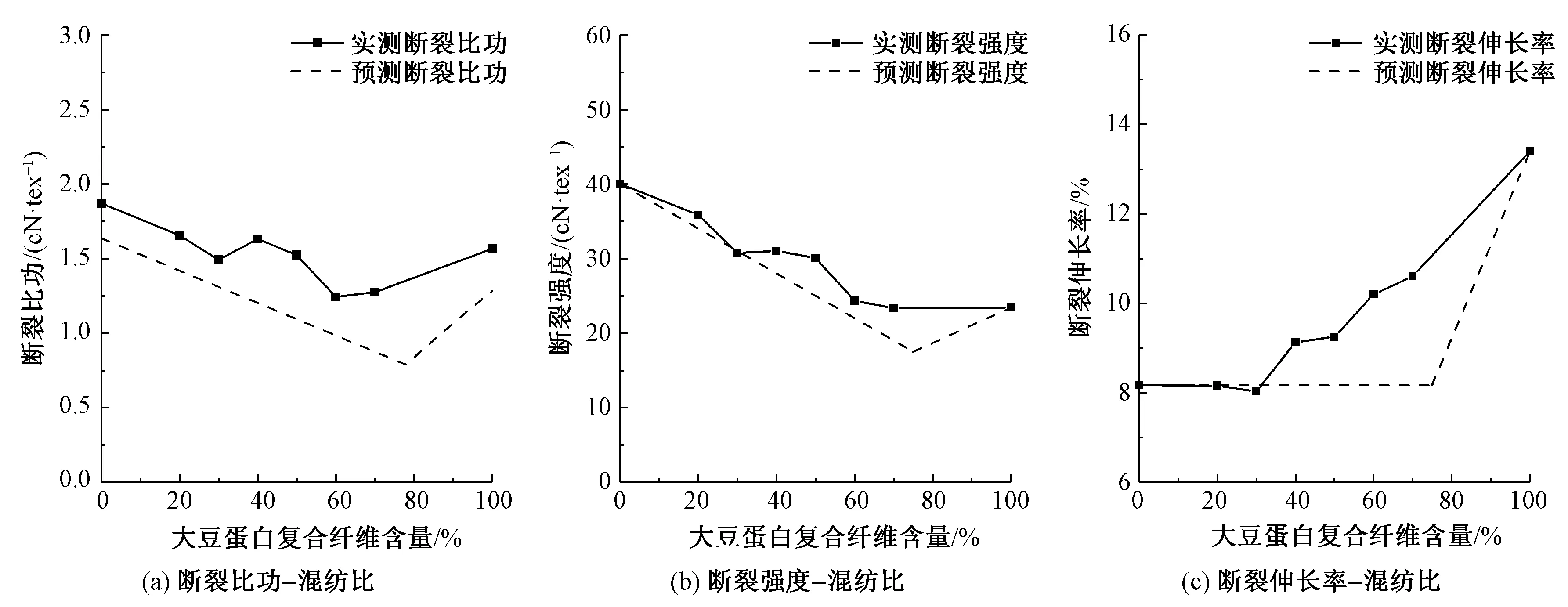
圖15 滌綸/大豆蛋白復合纖維混紡紗拉伸性能Fig.15 Tensile properties of polyester/soybean protein fiber yarn.(a)Specific work of rupture-blended ratio; (b)Tenacity-blended ratio; (c)Breaking extension-blended ratio

部分混紡實驗中,斷裂強度、斷裂伸長率和斷裂比功的預測結果仍存在一定誤差。斷裂比功的誤差與斷裂強度或斷裂伸長率的預測誤差相似,處于可接受范圍內。造成斷裂比功預測誤差的主要原因有2方面:對拉伸曲線的簡化以及斷裂強度、斷裂伸長率的預測誤差。一方面,混紡紗的實際拉伸曲線往往呈光滑的凹凸狀,而預測曲線被簡化為直線或折線,如圖5所示。實際曲線呈凸狀時,例如棉/竹漿纖維混紡和滌綸/大豆蛋白復合纖維混紡時,斷裂比功預測值就會偏小;相反,當實際曲線呈凹狀時,例如高比例腈氯綸混紡以及高比例羊毛混紡時,斷裂比功預測值就會偏大。另一方面,斷裂強度或斷裂伸長率的預測值偏大,斷裂比功預測值也會偏大;相反,斷裂強度或斷裂伸長率預測值偏小,例如棉/大豆蛋白復合纖維、棉/高強錦綸以及大麻/錦綸混紡,斷裂比功預測值也會偏小。

雖然預測結果存在一定誤差,但該關系式能較好地預測出斷裂比功隨混紡比變化的趨勢。

4 結 論

本文探究了雙組分混紡紗斷裂比功與混紡比的關系。通過對混紡紗斷裂過程的分析,提出了一種簡單的混紡紗拉伸曲線模型,并根據該模型建立了混紡紗斷裂比功與混紡比的關系式。由該式可知,與斷裂強度、斷裂伸長率相似,混紡紗斷裂比功隨混紡比變化的趨勢在臨界混紡比附近發生轉變。之后通過實驗數據驗證了該關系式的適用性與可靠性。該式為預測混紡紗的斷裂比功提供了一種簡單的方法,且預測誤差與現有的斷裂強度或斷裂伸長率表達式的預測誤差相似,處于可接受范圍內,為生產中合理地選擇混紡比提供了指導。

致謝感謝上海市現代紡織前沿科學研究基地對本文的資助。