智慧教室環境下培養初中生數形結合思想的實踐

陳國興

數學是一門研究數量、結構、變化、空間、信息等概念的學科。數形結合思想中的“數”與“形”分別對應數量關系與幾何圖形，是數學學習中兩項重要的內容。“數”“形”在一定條件下可以相互轉化，數形結合思想是解決數學問題的重要思想方法之一。在初中階段，培養學生的數形結合思想是落實核心素養培養任務的重要一環，而建設智慧教室，借助信息技術、互聯網絡等，打造直觀化、具象化的課堂，可以極大增強培養學生數形結合思想的實效性。

一、智慧教室與數形結合思想

（一）智慧教室

智慧教室是以信息化技術與多媒體融合為載體，利用智慧學習設備打造的新型教室。其由兩個核心部分組成：一是有形的物理空間，二是無形的數字信息空間。在智慧教室開展教學時，師生通過無線局域網絡和多種類型的“智慧屏幕”，可以同時獲取資源，隨時進行互動，從而打造新型教學環境。

（二）數形結合思想

數形結合是將數量關系與幾何圖形結合在一起，借助數量的精確性描述，闡釋幾何圖形的某些屬性，或借助圖形的直觀性描述，闡釋數量之間的關系，達到“以數解形”“以形助數”。在初中數學學習中，“數”與“形”是兩個關鍵部分，數形結合思想體現了直觀與抽象的統一，有助于學生在學習過程中將形象思維與抽象思維有機結合。

二、智慧教室環境下培養初中生數形結合思想的實踐

（一）電教設備呈現，直觀認識數形結合

有學者曾說：“數形結合百般好，割裂分家萬事休。”可見數形結合在數學學科中的重要性。而智慧教室具備了直觀呈現數形結合過程的條件，在智慧教室環境下，教師在教學中應從學生的形象思維出發，循序漸進地培養學生的數形結合思想。例如，在教授人教版初中數學七年級下冊第九章第三節“一元一次不等式組”相關內容時，教師可以利用電教設備，完整呈現數形結合思想在解決一元一次不等式組中的應用，讓學生直觀地感受數形結合的思維過程。

1.呈現主題，具象了解。教師可以向學生展示問題，讓學生以數軸形式求出下列不等式組的解集：

在解題過程中，學生結合學過的不等式知識，在數軸上會發現以上不等式組的解集未出現重合，從而從“形”的角度對一元一次不等式組獲得一定的認知。隨著解題的深入，學生會總結出規律，即數大取大、數小取小、大小與小大時在中間找解、大大小小情況無解，從“數”的角度對一元一次不等式組產生更深的認知。

2.抽象符號，數形結合。教師可以利用電教設備，將上述不等式組用符號表達，并以數軸還原解集（圖1）。教師還可以在多媒體屏幕上以動畫形式，呈現還原解集過程中的每一個步驟，確保每一個步驟與數量關系對應，使學生充分感受數形結合的思維過程。

3.基礎實踐，直觀體驗。教師可以提出問題：“假設不等式x-2＜a有正整數解，能否借助數軸確定a的取值范圍？”問題提出后，學生會通過數軸快速確定a的范圍。在此基礎上，教師可以逐步深化問題：“若不等式的正整數解有3個，該如何在數軸上確定？”在解答問題的過程中，學生先確定0≤x＜a+2，而解為正整數有3個，通過數軸可以看出在滿足條件下a+2應介于3與4之間（圖2）。為保證解為3個，a+2不能等于3，若等于3則只能保證有2個正整數解，a+2為4時則能夠滿足題目條件，因此，可以確定的取值范圍為3＜a+2≤4，拆分成不等式組? ? ? ? ? ? ? ? ?，經過計算得出1＜a≤2。

在以上三個環節的學習中，教師在電教設備的輔助下，引導學生總結在解決數學問題時運用數形結合思想的方法，感受數形結合的優勢，有助于學生在完整、直觀的感知過程中，客觀、全面地認識數形結合思想。

（二）智慧課堂互動，發展數形結合思維

智慧教室環境下的智慧課堂，是通過多媒體融合打造的高端課堂形態，能夠為師生互動提供多種渠道。教師在教學實踐中要充分利用智慧課堂的優勢，與學生開展深度互動，引導學生運用數形結合思想看待問題、解決問題，培養學生的數形結合思維。例如，在人教版初中數學八年級上冊第十二章第三節“角的平分線的性質”的學習中，學生需要掌握的知識包括通過三角形的角平分線構造全等三角形、證明三角形全等。在教學過程中，教師可以充分利用智慧教室中的電教設備，引導學生積極參與課堂互動，培養學生的數形結合思維。

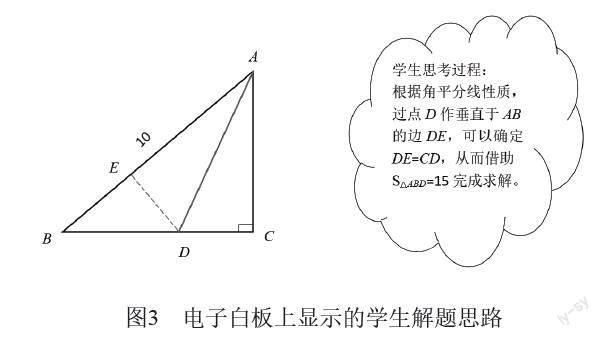
1.電子白板互動。教師可以在電子白板上向全班學生呈現如下例題，引發學生思考。例題1：“在△ABD中，已知∠C為90°，AD是∠BAC的平分線，與BC相交于點D。其中AB=10，S△ABD=15，求CD長。”

2.學生響應系統。教師可以利用手持設備詢問學生關于解答例題1的思路。這樣，學生可以單獨回答教師的問題，避免干擾其他同學的思路。在此過程中，教師可以將知識條件體現在題目的圖示中，更深入地挖掘題目的已知信息，幫助學生更直觀地理解已知條件與數量關系。

3.互動投影。在確定解題思路后，學生可以利用手勢在電子白板顯示的課件上通過拖拽、畫圖等方式完成操作，將自身基于數形結合思想的思考呈現在電子白板上（圖3）。其他學生有了新的解題思路時，也可以在電子白板上利用不同顏色的線條或文字進行表達，給予學生充分參與課堂的機會。

4.平板電腦互動。學生可以按照上個環節確定的解題思路，在平板電腦上寫出解題過程并上傳至學習平臺，教師與其他學生均可同步看到答案。基于此，學生之間可以實現共享和交流，并在此過程中學習數學語言的表述，加深對數形結合的理解。

在智慧課堂，多樣化的互動途徑能夠為學生提供體驗數形結合的契機，促進學生基于數形結合展開豐富且有深度的交流，從而保證學生充分參與課堂，實現數形結合思維的有效發展。

（三）人機交互練習，強化數形結合意識

在練習中感知數形結合，是學生快速形成數形結合意識，自覺利用數形結合思考與解決問題的重要路徑。在智慧教室環境下，人機交互練習方式擺脫了枯燥、機械的傳統練習模式，有利于激發學生的練習興趣。在此過程中，教師要高效分享資源、實時互動，密切關注不同層次學生的練習需求。教師在傳遞習題資源時，可以設置不同難度的模塊，告知學生可以根據需求先從基礎模塊做起，攻克基礎題目后再挑戰中級題目，在進階式的練習中持續增強學生的數形結合意識。

例如，在教授人教版初中數學九年級下冊第二十六章“反比例函數”之后，教師可以在線上學習平臺上傳包含反比例函數基礎知識、與一次或二次函數結合、與幾何圖形結合、與實際生活結合的練習題。其中，基礎知識及與一次或二次函數結合的習題為基礎題目，與幾何圖形結合的習題為中級題目，與實際生活結合的習題為高級題目。學生在學習平臺上找到習題庫后，點擊對應標題即可獲取習題資源。在學生做題的過程中，教師通過線上平臺可以隨時掌握學生的答題情況。當觀察到全部學生完成了基礎習題、絕大多數學生完成了中級習題，且10分鐘時間內高級習題正確率未上升時，教師可以直接在線上平臺切換角色，選擇一名做對習題的學生當“小老師”，在學習平臺上演示高級習題的解題思路、過程，方便學生彼此借鑒數形結合思想方法的運用經驗，彌補知識和認識上的不足。

（四）多屏協同共享，發散數形結合思維

智慧教室環境下，教學空間與資源不再受限，教師在課堂上可以基于多屏共享拓寬學生視野，從多方面滲透數形結合思想，培養學生的發散思維，提高學生舉一反三、觸類旁通的能力。例如，在人教版初中數學九年級上冊第二十四章第二節“點和圓、直線和圓的位置關系”的教學中，為了延伸課堂，教師可以基于教師用屏、小組用屏和學生用屏，引導學生探索知識，應用數形結合思維解答問題。

首先，在教師用屏上，呈現核心知識點與數學問題。教師可以將學生自主繪制的思維導圖呈現在教師用屏上，并設置如下題目。

例題2：如圖4，四邊形ABCD內接于⊙O，AB為⊙O直徑，已知AD=CD.

1.根據圖a，求證∠ABC=2∠ACD；

2.如圖b，過點D作⊙O切線，交BC延長線于點P，假設tan∠CAB=，BC=1，求PD長。

其次，在小組用屏上（教室墻面上安裝的可觸摸一體機），要求學生以小組探究形式解決題目。學生可以應用小組用屏，將數量與圖形之間的關系直觀地呈現在屏幕上。例如，有小組在解決例題2時，通過小組用屏直接連接OD與OC，發現了解題突破口。但有小組經過反復嘗試未能發現解答∠ABC與∠ACD之間關系的突破口。此時，學生可以點擊屏幕上的“提示”功能鍵，教師在收到消息后，可以及時為該小組傳遞資源給予提示，如其他組的解題思路等。

最后，在學生用屏上，教師可以通過局域網共享各個小組的探究成果，以視頻的方式呈現小組探究中的一系列學習行為，實現深層交互，從而提高學生對數形結合思想的應用能力，促進學生發散思維。如大多數小組在解決例題2時做了輔助線OD，但有個別學生提出“不做輔助線的情況下能否求解”這一問題。針對該問題，各小組重新梳理圖形與數量之間的關系，探索新的解題方法，進一步加深了對數形結合思想的理解。

（作者單位：福清市高山育才中學）