創(chuàng)設(shè)尋共辨異的教學(xué)情境
——以“中點(diǎn)四邊形”教學(xué)設(shè)計(jì)為例

廣東省東莞市南城陽光實(shí)驗(yàn)中學(xué)(523000)鄭珍

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2022 年版)》在課程理念中明確指出要實(shí)施促進(jìn)學(xué)生發(fā)展的教學(xué)活動.教師應(yīng)基于學(xué)生的經(jīng)驗(yàn),體現(xiàn)數(shù)學(xué)學(xué)科本質(zhì),挖據(jù)學(xué)習(xí)內(nèi)容的多維邏輯性,引導(dǎo)學(xué)生經(jīng)歷數(shù)學(xué)知識的形成過程, 了解相關(guān)內(nèi)容的內(nèi)在關(guān)聯(lián),發(fā)展核心素養(yǎng).因此,教學(xué)中盡可能多地創(chuàng)設(shè)與已有知識密切關(guān)聯(lián),同時又需要獨(dú)立思考辨別的教學(xué)情境——尋同辨異.他的核心是將陌生對象與熟悉對象、未知規(guī)律與已知規(guī)律相互轉(zhuǎn)化,促進(jìn)學(xué)生形成發(fā)現(xiàn)問題的意識,培養(yǎng)學(xué)生分析解決問題的能力,進(jìn)而促進(jìn)學(xué)生核心素養(yǎng)的形成與發(fā)展.本文就結(jié)合初中數(shù)學(xué)“中點(diǎn)四邊形”教學(xué)設(shè)計(jì)為主題談?wù)勅绾蝿?chuàng)設(shè)尋共辨異的教學(xué)情境.

1 內(nèi)容分析

人教版初中數(shù)學(xué)(八年級下冊)第十八章平行四邊形的習(xí)題中,出現(xiàn)了“中點(diǎn)四邊形”.本課是在學(xué)生學(xué)習(xí)了平行四邊形、矩形、菱形、正方形的性質(zhì)和判定及三角形中位線的性質(zhì)后設(shè)置的一節(jié)探究專題課.學(xué)生對利用中點(diǎn)添加輔助線構(gòu)造中位線已有初步經(jīng)驗(yàn),但還未能運(yùn)用自如.對于為什么會出現(xiàn)中點(diǎn)四邊形這個知識? 它又與前面所學(xué)知識的內(nèi)在聯(lián)系是什么? 如何探究這個問題? 學(xué)生對于以上問題還不清楚,所以本節(jié)課通過創(chuàng)設(shè)“判定中點(diǎn)三角形”這個知識情境來引入探究四邊形的中點(diǎn)四邊形的形狀,使學(xué)生感受新舊知識的關(guān)聯(lián)性,以及探究新問題的一般路徑和方法.基于以上分析,確定如下教學(xué)目標(biāo)和教學(xué)重、難點(diǎn).

教學(xué)目標(biāo): (1)能夠直接說出常見四邊形的中點(diǎn)四邊形的形狀;(2)參與中點(diǎn)四邊形形狀的探究,體驗(yàn)數(shù)學(xué)發(fā)現(xiàn)的過程;(3)感受知識的密切關(guān)聯(lián),體會研究問題的一般策略和方法.

教學(xué)重點(diǎn): 根據(jù)原四邊形對角線的關(guān)系探究中點(diǎn)四邊形的形狀.

教學(xué)重點(diǎn): 根據(jù)原四邊形對角線的關(guān)系探究中點(diǎn)四邊形的形狀.

2 情境設(shè)計(jì)過程

2.1 分析情境需求

布魯納在《教育過程》中指出,學(xué)習(xí)者在不斷地、主動地完善和發(fā)展自己的認(rèn)知結(jié)構(gòu)的過程就是學(xué)習(xí)者在參與學(xué)習(xí)活動的表現(xiàn).教師除了要關(guān)注學(xué)生數(shù)學(xué)知識與技能的積累,還要關(guān)注學(xué)生對隱藏在知識背后的知識間的關(guān)聯(lián),即知識之間的結(jié)構(gòu)聯(lián)系的認(rèn)識與構(gòu)建.所以,教師在創(chuàng)設(shè)情境時需要分析知識之間內(nèi)在的聯(lián)系與結(jié)構(gòu),尋找新、舊知識的共同點(diǎn),讓學(xué)生覺得新知自然引出.

學(xué)生在學(xué)習(xí)中點(diǎn)四邊前已經(jīng)學(xué)習(xí)了三角形形狀的判定和三角形中位線等相關(guān)知識,而本節(jié)課的重點(diǎn)就是利用三角形的中位線探究中點(diǎn)四邊形的形狀,所以這兩部分知識存在著密切關(guān)聯(lián).接下來教師就是要在舊知的基礎(chǔ)上思考授課新知的切入點(diǎn).

2.2 設(shè)置恰當(dāng)問題

哈爾莫斯曾說:“問題是數(shù)學(xué)的心臟.”愛因斯.坦曾說:提出一個問題往往比解決一個問題更重要.”所以我們老師在復(fù)習(xí)舊知時要合理設(shè)置問題,所設(shè)計(jì)的問題要既能體現(xiàn)學(xué)生的認(rèn)知發(fā)展水平,又符合數(shù)學(xué)知識的發(fā)生發(fā)展的順序.這就要求老師們設(shè)計(jì)尋同辨異的數(shù)學(xué)情境,在學(xué)生感受到在回顧舊知的知識基礎(chǔ)上自然過渡到新知,自覺思考聯(lián)系,進(jìn)而引領(lǐng)后續(xù)的探究活動.

活動1: 復(fù)習(xí)回顧中點(diǎn)三角形的概念

問題1: 請任意畫出一個三角形,并分別找到各邊的中點(diǎn).

設(shè)計(jì)意圖: 通過讓學(xué)生動手尋找三角形各邊中點(diǎn),了解圖形的生成過程;同時為接下來找四邊形的中點(diǎn)做鋪墊.如圖1,點(diǎn)D、E、F分別是ΔABC的

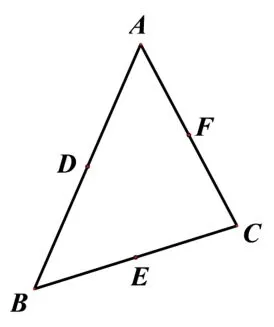
圖1 三角形各邊中點(diǎn)

追問1: 根據(jù)你所畫的圖形,你最想連的線段是哪些?

設(shè)計(jì)意圖: 讓學(xué)生主動聯(lián)想有關(guān)中點(diǎn)的相關(guān)知識,能夠幫助學(xué)生鍛煉思維,再次感受圖形的產(chǎn)生過程以及為什么要添加輔助線.

追問2: 三角形的中位線有哪些性質(zhì)?

設(shè)計(jì)意圖: 三角形中位線的性質(zhì)是知識的最近發(fā)展區(qū),它是本課時探究學(xué)習(xí)的理論基礎(chǔ),同時它是我們證明兩條線段間的關(guān)系包含數(shù)量關(guān)系與位置關(guān)系的重要方法.本節(jié)課重點(diǎn)就是根據(jù)原四邊形的對角線的關(guān)系利用三角形的中位線證明中點(diǎn)四邊形鄰邊關(guān)系.如圖2,DF是ΔABC的一條中位線,可以得到DF//BC,.

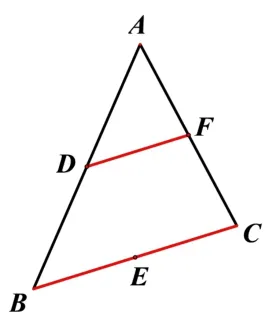
圖2 三角形的中位線

問題2: 依次連接三角形各邊中點(diǎn),得到的三角形叫什么三角形?

設(shè)計(jì)意圖: 復(fù)習(xí)中點(diǎn)三角形的概念,為中點(diǎn)四邊形概念的提出做鋪墊.

追問1: 等腰三角形、直角三角形的中點(diǎn)三角形分別是什么三角形? 為什么?

設(shè)計(jì)意圖: 通過對中點(diǎn)三角形形狀的判別,讓學(xué)生復(fù)習(xí)中位線并熟悉中位線的應(yīng)用;同時順理成章地引入本節(jié)課的主題——中點(diǎn)四邊形形狀的判別.讓學(xué)生用不同的方法自己說出中點(diǎn)三角形的形狀是如何判別的,這一過程所用到的知識、方法、技能就是本節(jié)課證明中點(diǎn)四邊形形狀所用的.

如圖3,ΔDEF是ΔABC的中點(diǎn)三角形,且AB=AC,判斷ΔDEF的形狀.

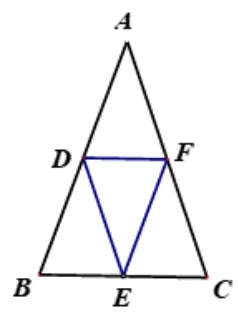
圖3 等腰三角形

學(xué)生簡答: ∵DE、EF是ΔABC的中位線∴;又∵AB=AC;∴DE=EF,∴ΔDEF是等腰三角形.

如圖4,ΔDEF是ΔABC的中點(diǎn)三角形,且∠C=90°,判斷ΔDEF的形狀.

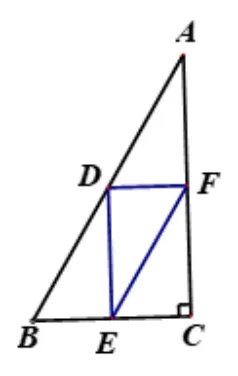
圖4 直角三角形

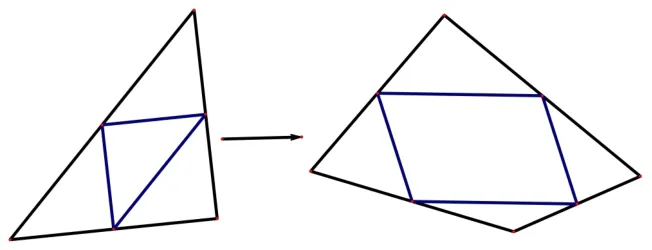
圖5 從中點(diǎn)三角形到中點(diǎn)四邊形

圖6 構(gòu)造三角形的中位線

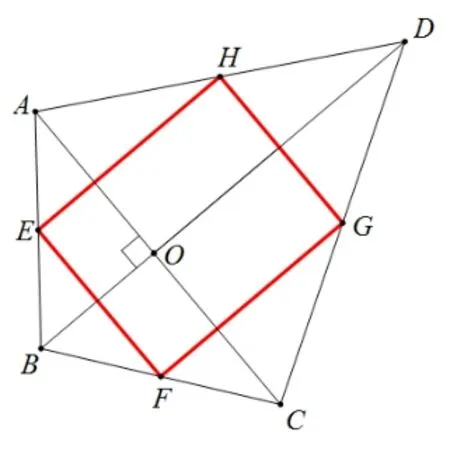
圖7 原四邊形對角線相互垂直

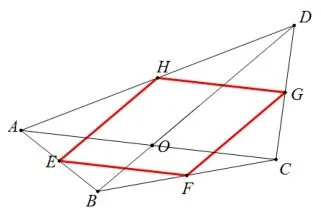
圖8 原四邊形對角線相等

學(xué)生簡答: ∵DE是ΔABC的中位線, ∴DE//AC,∴∠DEC= ∠C= 90°, 又∵EF是ΔABC的中位線,∴FE//AB, ∴∠EDF= ∠DEC= 90°, ∴ΔDEF是直角三角形.

教師總結(jié): 三角形的形狀是由邊的數(shù)量和位置關(guān)系決定的, 即如圖3 中DE、EF的數(shù)量關(guān)系和如圖4 中DE、DF的位置關(guān)系,而DE、EF、DF中位線之間的關(guān)系又是由它們各自所對的第三邊之間的關(guān)系.

設(shè)計(jì)意圖: 這個問題是本節(jié)課的核心,如果直接問學(xué)生中點(diǎn)三角形的形狀與原三角形直接的關(guān)系,學(xué)生的想法開始肯定外面是什么三角形, 里面中點(diǎn)三角形也是什么三角形.這樣在接下來我們探究中點(diǎn)四邊形的形狀時會帶來錯覺.所以,此處沒有直接問學(xué)生,而是老師總結(jié)出中位線間的關(guān)系與它們所對的第三邊間的關(guān)系是一致的.這樣為我們后面的研究指明思考方向.

3 情境設(shè)計(jì)效果

通過前面創(chuàng)設(shè)中點(diǎn)三角形的教學(xué)情境,我們就可以順利的引出中點(diǎn)四邊形的概念以及如何來探究證明中點(diǎn)四邊形的形狀,最終讓學(xué)生討論得到原四邊形對角線的關(guān)系決定中點(diǎn)四邊形的形狀.這樣既可以幫助學(xué)生更好地掌握新舊知識間的關(guān)聯(lián),構(gòu)建屬于自已的知識體系;又可以引導(dǎo)學(xué)生從關(guān)注知識本身轉(zhuǎn)向關(guān)注知識發(fā)展中所涉及的研究路徑與方法.

3.1 新知引入自然

情境設(shè)置中講到中點(diǎn)三角形的概念: 連接各邊中點(diǎn)所圍成的三角形是中點(diǎn)三角形;那么我們類比自然可以得到中點(diǎn)四邊形的概念: 順次連接四邊形各邊中點(diǎn),得到的四邊形叫中點(diǎn)四邊形.但是,這兩個概念要讓學(xué)生辨析區(qū)別.概念引出后, 是判斷中點(diǎn)四邊形的形狀, 這也跟情境中設(shè)置的問題2中的第2 個追問: 特殊三角形的中點(diǎn)三角形的形狀的判斷相對應(yīng)的.同樣,這里也是有區(qū)別的,我們是從一般的四邊形的中點(diǎn)四邊形的形狀判斷開始的.

3.2 研究路徑通暢

我們開始復(fù)習(xí)了判斷中點(diǎn)三角形的形狀的路徑和方法,那就是情境中最后老師的總結(jié)部分: 中位線間的關(guān)系與它們所對的第三邊間的關(guān)系是一致的,利用這個知識可以證明中點(diǎn)三三角形的形狀.現(xiàn)在,中點(diǎn)四邊形同樣圖形中有很多中點(diǎn),學(xué)生自然想到中位線.但是,這里有相同點(diǎn),同樣也有區(qū)別;那就是中點(diǎn)四邊形中沒有中位線的模型.這里要引導(dǎo)學(xué)生通過辨析區(qū)別,構(gòu)造共性,所以學(xué)生順理成章想得連接對角線.

學(xué)生通過連接一條對角線,很快有學(xué)生會頓悟到一般四邊形的中點(diǎn)四邊形是平行四邊形, 然后小組討論如何證明.當(dāng)然這里大家的證明方法有多種,讓學(xué)生展示給大家.特別是連接兩條對角線的,因?yàn)檫@為我們特殊四邊形的中點(diǎn)四邊形的形狀的判斷提供方向.

接下來,然學(xué)生探究下面兩類特殊的四邊形的中點(diǎn)四邊形的形狀,這與我們情境中設(shè)置的問題2 中的第2 個追問相對應(yīng).學(xué)生通過探討可以得到: 對角線相互垂直的四邊形的中點(diǎn)四邊形是矩形;對角線相等的四邊形的中點(diǎn)四邊形是菱形.接著,讓學(xué)生思考討論: 中點(diǎn)四邊形的形狀究竟由原四邊形的哪個因素決定的? 這個問題的設(shè)置對應(yīng)了情境中最后老師總結(jié): 中位線間的關(guān)系與它們所對的第三邊間的關(guān)系是一致的.學(xué)生經(jīng)過獨(dú)立思考和小組討論后可以得到: 中點(diǎn)四邊形的形狀由原四邊形的兩條對角線的數(shù)量與位置關(guān)系所決定.

4 結(jié)束語

本文重點(diǎn)通過舉例說明創(chuàng)設(shè)“尋共辨異”的教學(xué)情境可以幫助學(xué)生利用原有的知識結(jié)構(gòu)類比學(xué)習(xí)促進(jìn)新知的獲得,進(jìn)一步優(yōu)化學(xué)生的知識網(wǎng)絡(luò),形成獨(dú)立探討問題的路徑與方法,進(jìn)而達(dá)到增強(qiáng)核心素養(yǎng)的目的.所以,在平時的教學(xué)中,我們在準(zhǔn)備一節(jié)課時,必須要站在學(xué)生的角度全盤考慮,整體把握教學(xué)內(nèi)容,積極開展蘊(yùn)含尋共辨異情境的教學(xué)設(shè)計(jì)的探究十分必要.