拼補法在解中考幾何問題中的運用*

太原師范學院數學與統計學院(030619)李露 韓龍淑

1 問題提出

平面幾何作為中考數學重點考查的內容,既是教師教的難點,也是學生學的難點[1].《義務教育數學課程標準(2022年版)》指出: 應發展學生運用數學知識與方法發現、提出、分析和解決問題的能力[2].因此,教師應幫助學生合理運用解題方法提升分析和解決中考幾何問題的能力.而拼補法是解決幾何問題的方法之一,合理運用拼補法有利于探尋中考幾何問題的解決路徑,提高解題效率和準確性.

拼補法主要指把原有圖形拼補成一個基本圖形,一般是把不規則圖形補為平行四邊形、三角形、梯形等,分別求出相關基本圖形的數量關系,再利用已知的基本圖形求未知的數量條件.即通過整體求局部的方法.學生掌握拼補法的數學方法,可以解決同類特征的幾何問題,從而實現快速尋求和發現解決中考幾何問題的思路與途徑.因此,研究適合運用拼補法的題型及特征就顯得特別有現實意義.

2 拼補法在解中考幾何問題中的運用

通過分析拼補法解決中考幾何問題的題型及特征,發現運用拼補法所解決的中考幾何問題可以分為以下兩種類型:含有特殊點的幾何問題和含有特殊角的幾何問題.對于含有特殊角的幾何問題又可以分為兩類: 構造含有特殊角的直角三角形和構造含有特殊角的等邊三角形.

2.1 運用拼補法解決含有特殊點的中考幾何問題

對于條件中含有特殊點的中考幾何問題,可以利用特殊點的相關結論去拼補圖形,例如含有中點的線段考慮運用中位線定理,將圖形補成三角形或梯形,把不規則幾何圖形轉化為基本幾何圖形,從而找到問題解決的思路.

例1(2017 年山西卷第15題) 一副三角板按如圖1 所示方式擺放, 得到ΔABD和ΔBCD,其中∠ADB= ∠BCD= 90°,∠A= 60°, ∠CBD= 45°,E為AB中點,過點E做EF⊥CD于點F,若AD=4cm,則EF的長為____cm.

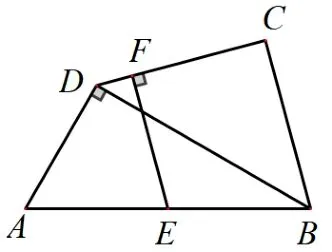
圖1

分析該題是在不規則幾何圖形中求EF的長度,但EF的長度不易直接求出,而點E為線段AB中點,解決該類特殊點問題時則可以運用拼補法, 如圖2 所示, 線段EF為所補圖形的中位線,進而運用梯形中位線定理得出線段EF的長度.因為EF⊥CD,BC⊥CD,所以EF//BC.E為AB中點,可以過A做BC的平行線AG交CD延長線于點G,則AG//BC.綜上所述,EF為直角梯形BCGA的中位線,進而求得EF的長度.

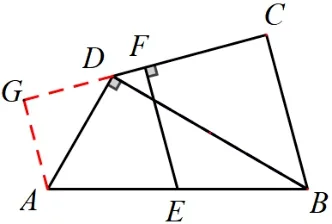
圖2

解析如圖2 所示,根據梯形中位線定理可知,要求EF的長度, 就要求BC和AG的長度.因為∠CDB= 45°,∠BDA= 90°, 所以∠GDA= 45°.而∠G= 90°, 所以ΔAGD為等腰直角三角形.AD= 4cm,ΔBCD為等腰直角三角形,, 所以,根據梯形中位線定理可以計算出.

通過此題可以發現含有特殊點的幾何圖形運用拼補法能夠快速找到解題思路和解題步驟,將不規則幾何圖形轉化為規則幾何圖形, 然后運用梯形中位線定理求出線段長度,學生在已有的知識基礎上快速解決中考幾何問題.

2.2 運用拼補法解決含有特殊角的中考幾何問題

對于問題條件中含有特殊角的問題來講,可將含有特殊角的圖形拼形為常見的特殊三角形.其中特殊角是指30°,45°,60°,120°,135°,150°的角,將含特殊角的圖形拼形為直角三角形去解決幾何問題;除此以外,含特殊角60°,120°的圖形還可拼形為等邊三角形去解決幾何問題.

運用含特殊角解決問題的方法能夠把題目中不易求解的幾何圖形通過補形轉化成易求解的幾何圖形,從而找到幾何問題的解決路徑,發展學生分析并解決問題的能力.

2.2.1 運用拼補法構造含有特殊角的直角三角形

何時考慮運用拼補法構造特殊角的直角三角形呢? 考慮以下條件是否滿足.圖形中含有30°,45°,60°,120°,135°,150°的角,且該特殊角或補角與所求量可放在一個基本圖形中,那么可考慮使用拼補法構造含特殊角的直角三角形.

例2(2014 年山西卷第16 題)如圖3, 在ΔABC中, ∠BAC= 30°,AB=AC.AD是BC邊上的中線,,CE交AB于點E, 交AD于點F.若BC=2,則EF的長為____.

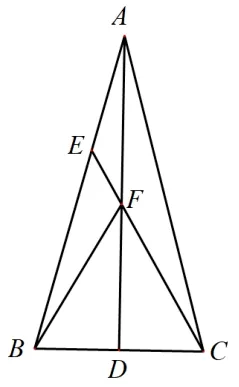
圖3

分析在現有圖形中無法直接求出EF的長度.但由已知條件可得,∠AFE= ∠DAC+ ∠ACF= 15°+ 15°= 30°,EF所在三角形ΔAEF為含有30°特殊角的圖形,因此可考慮運用拼補法構造直角三角形ΔANF,如圖4 所示.在ΔANF中求出EF的長度.

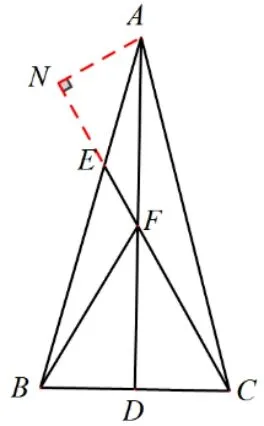
圖4

解析過點A做AN⊥FE,與FE的延長線交于點N.如圖4 所示, 因為AB=AC, 所以ΔABC為等腰三角形.∠BAC= 30°,AD是BC邊上的中線, 所以∠FAC= ∠FAE=15°.因為, 所以∠ACF= 15°, ∠BCF= 60°.ΔAFC為等腰三角形, ΔBFC為等邊三角形.∠AFE= 30°, ∠NAF= 60°, ∠NAE= 45°, ΔANE為等腰直角三角形.因為BC= 2, 所以CF=AF= 2,AN=NE=1,,于是.

在此問題中, 通過∠AFE= 30°這個特殊角, 構造直角三角形ΔANF,結合已知條件計算各線段長度即可得出EF的長.而此題的關鍵突破口在于運用拼補法構造含有已知特殊角的直角三角形.

2.2.2 運用拼補法構造含有特殊角的等邊三角形

例3(2021 年山西卷第20 題)圖算法也叫諾模圖,是根據幾何原理,將某一已知函數關系式中的各變量,分別編成有刻度的直線(或曲線),并把它們按一定的規律排列在一起的一種圖形,可以用來解函數式中的未知量.比如想知道10攝氏度相當于多少華氏度,我們可根據攝氏溫度與華氏溫度之間的關系:得出,當C= 10 時,F= 50.但是如果你的溫度計上有華氏溫標刻度,就可以從溫度計上直接讀出答案,這種利用特制的線條進行計算的方法就是圖算法.

再看一個例子: 設有兩只電阻, 分別為5 千歐和7.5 千歐,問并聯后的電阻值是多少?

任務:

(1)請根據以上材料簡要說明圖算法的優越性;

(2)請用以下兩種方法驗證第二個例子中圖算法的正確性:

②如圖5, 在ΔAOB中,∠AOB= 120°,OC是∠AOB的角平分線,OA= 7.5,OB=5, 用你所學的幾何知識求線段OC的長.

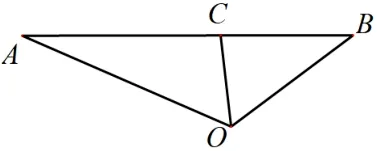
圖5

解析(1)優越性: 略.

(2) ①只需要將數值代入, 即可得到R值結果.R1= 7.5,R2= 5 時,,所以R=3.

②解法如下.

如圖5 所示,已知∠AOB= 120°為特殊角,而對于含有60°或120°的特殊角除運用拼補法構造直角三角形以外,還可以反向延長構造等邊三角形.

分析因為ΔAOB中含有特殊角∠AOB=120°,那么延長BO交AG于點G,如圖6 所示,使得OA=OG,連接AG,即可得到一個含特殊角60°的等邊三角形ΔAOG.由“內錯角相等,兩直線平行”可以判定OC//GA,進而通過相似求出OC的長.

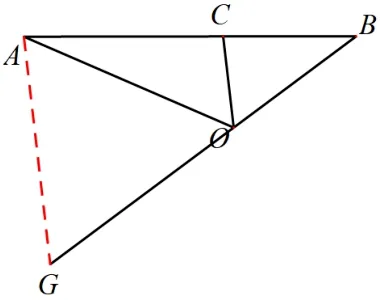
圖6

解析如圖6 所示,延長BO交AG于點G,使得OA=OG,連接AG.因為OA=OG,∠AOG= 60°, 所以ΔAOG為等邊三角形, 則AG=OA=7.5.又因為∠OAG=∠COA=60°, 所以OC//GA, ΔBCO～ΔBAG.則,所以OC=3.

通過上述解法發現含有特殊角的幾何圖形可運用拼補法將其補為等邊三角形,等邊三角形的特殊性使學生更易想到解決問題的思路.在等邊三角形中,求出一條邊便可知另外兩邊長度.在求出AG長度的基礎上借助相似三角形的對應線段成比例,即可求得OC的長.

3 教學啟示

3.1 借助“拼補法”的題型特征,探尋問題解決的突破口

數學是以思維為主的科學,數學解題對培養學生的思維能力具有特殊的功能.尋求正確的解題思維和方法,找出問題解決的途徑,是數學學習中的重要內容[3].在以上中考幾何問題中,構造輔助幾何圖形是重要的思維活動.若學生具有將所求線段含有特殊點、特殊角的幾何圖形與構造輔助幾何圖形建立自然的、內在聯系的意識,抓住問題的特征,便可突破植根于構造輔助幾何圖形的大量題目.因此,抓住運用拼補法的題型特征,有利于學生快速找到問題的解決路徑.

反思以上中考題目,都是借助題型特征通過補形構造基本圖形解決問題.例1 通過特殊點E 構造直角梯形求出線段EF的長度.例2 借助特殊角構造直角三角形求出EF的長度.例3 通過特殊角構造等邊三角形求出OC的長度.由此可知,運用拼補法的關鍵在于所求線段是否與幾何圖形中的特殊點、特殊角有關聯,借助題型特征構造出與已知幾何圖形具有實質性聯系的基本圖形,從而找到問題解決的突破口.

3.2 建立幾何圖形之間的相似關系,追求解題思路的自然生成

數學學習離不開解題,但數學學習的主要任務并不是解題,應當通過解一個題目或者幾個題目發現題型特征,揭示出該類具體情形中的一般模型,獲得解決一類問題的數學機智[4].反思以上中考題目的解法,發現運用拼補法構造幾何圖形,使得待求線段所在的幾何圖形與其他圖形之間可以通過相似關系找到問題的突破口,從而獲得簡單、自然的解題思路.

在以上解法中,例1 中E為中點,通過特殊點聯想到利用梯形中位線定理求出線段EF的長度,而梯形中位線定理是利用三角形相似的性質得到的.例3 中通過探尋OC所在幾何圖形與其他相似圖形之間的關系求得長度.因此,在根據題型特征構造的幾何圖形中,需要多分析和思考待求線段所在的幾何圖形與其他圖形之間的相似關系,從而自然地找到解題思路,避免學生陷入思維在同一層次、低水平的瑣碎運算中,也為以后遇到類似情境提供簡單、自然的解決方案.

3.3 滲透解決幾何問題的思想方法,發展學生的學科核心素養

《義務教育數學課程標準(2022 年版)》指出核心素養導向的教學目標是對“四基”“四能”教學目標的繼承和發展.“四基”“四能”是發展學生核心素養的有效載體.因此,在幾何問題的解題過程中,可以通過基礎知識和基本思想方法提升學生分析問題、解決問題的能力,從而發展學生的數學學科核心素養.在面對含有特殊點、特殊角的幾何問題時,教師可引導學生運用拼補法將復雜、抽象和困難的幾何問題運用化歸思想轉化為簡單、直觀和易解決的幾何問題,從而提升學生解決幾何問題的水平和效率[5].

幾何解題的教學中不能僅停留在解題、講題層面,更要滲透解決幾何問題的思想方法[6].以上中考幾何題運用拼補法構造基本幾何圖形后,例1 中EF由不易直接求出其長度化歸為求中位線問題.例2 中EF由不易直接求出其長度化歸為求直角三角形邊長問題.例3 中OC由無法直接求出其長度化歸為三角形相似的求值問題.由此可見,在幾何問題的教學過程中滲透拼補法和化歸思想,可以將不易直接求解的幾何問題簡單化,有助于學生尋找求解幾何問題的切入點,提高解題能力[7].同時,在運用數學思想方法分析問題和解決問題的過程中,優化學生的數學思維品質,發展幾何直觀和邏輯推理等學科核心素養.