基于SOLO 分類理論的高考數學復習實踐探索
——以導數解答題的復習為例

廣東省廣州市廣州中學(510630)方金財

《普通高中數學課程標準(2017 年版)》中明確強調數學教育要“以人為本”,尊重學生主體地位,因材施教,實現不同的個體在數學上可以得到不同程度的綜合發展,提高課堂教學的綜合質量,滿足不同學生的各種需求.高考中的導數解答題往往以難度較大的綜合壓軸題出現,學生做起來耗時長,得分低.大部分同學在復習這部分知識時容易陷入難的不會做,容易的不愿做的困境.教師在教學中也常常難以取舍,題目設置得太簡單就與考試試題呈現方式相違,題目設置得太難,學生做不出來,打擊了自信心.本文中筆者將以導數解答題的復習為例闡述運用SOLO 分類理論復習的實踐探索,以期能對同行在高考復習中有所幫助.

1 SOLO 分類理論介紹

SOLO 分類理論是由彼格斯在皮亞杰認知階段理論的基礎上,將學習結果按照復雜程度依次劃分成五個層次: 前結構水平(P 水平)、單點結構水平(U 水平)、多點結構水平(M水平)、關聯結構水平(R 水平)以及抽象拓展水平(EA 水平).

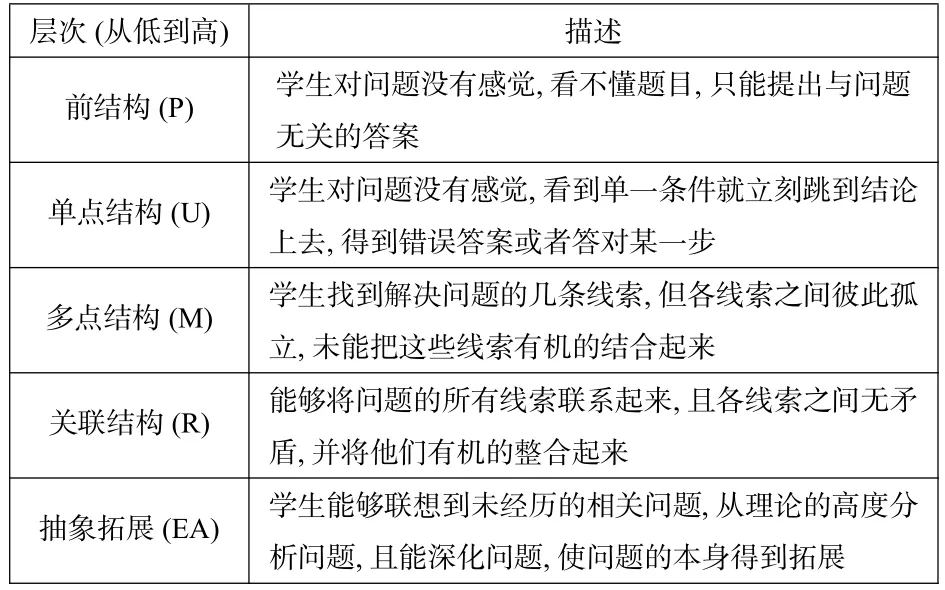
表1 SOLO 分類理論的層次說明

2 運用SOLO 分類理論分析近四年新課標Ⅰ卷導數解答題考點思維層次和特點,明確考情

2.1 舉例說明SOLO 分類理論在分析高考導數解答題考點思維層次的應用

例1(2023 新課標Ⅰ卷第19 題) 已知函數f(x) =a(ex+a)-x.(1)討論f(x)的單調性; (2)證明: 當a＞0時,.

此題(1)考察函數求導、參數討論、導數值正負判斷、確定單調區間,整合多個單點結構解決問題,屬于多點結構.(2)考察構造函數,結合函數的單調區間、極值點求出最小值,證明不等式恒成立,屬于關聯結構.

例2(2022 新課標Ⅰ卷第22 題)已知函數f(x)=ex-ax和g(x)=ax-lnx有相同的最小值(1)求a;(2)證明: 存在直線y=b,其與兩條曲線y=f(x)和y=g(x)共有三個不同的交點,并且從左到右的三個交點的橫坐標成等差數列.

此題在(1)中需求出兩個函數的最小值,兩個最小值相等需要解一個超越方程,猜出方程的解,再構造函數由函數的單調性得到a的唯一值,屬于關聯結構.在(2)中需討論b的不同取值,運用零點存在性定理判斷直線與兩個函數的交點個數.得到三個交點后又需要找到三個交點坐標的關系,并證明成等差數列,解決此問題需要達到抽象拓展水平.

2.2 近4 年新課標Ⅰ卷高考題考查知識點統計及SOLO層次分析

由于筆者所在廣東省使用新課標Ⅰ卷,所以在備考時主要還是側重研究新課標Ⅰ卷.(見表2)

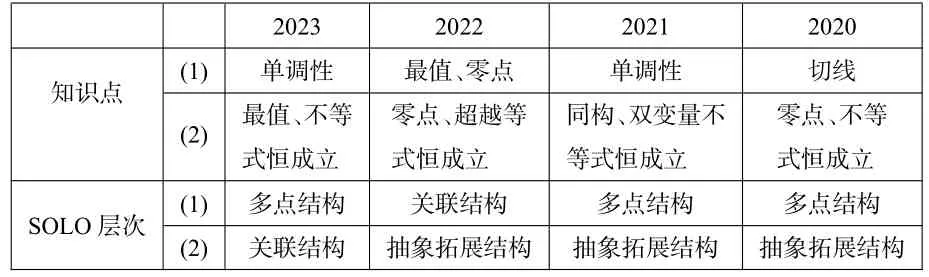
表2 近4 年Ⅰ卷高考導數解答題SOLO 分類理論層次分析統計

2.3 近4 年新課標Ⅰ卷高考題導數解答題特點

(1)第一問多為多點結構、關聯結構的基礎題,中檔題.

(2)第二問考察的思維層次較高,達到了抽象拓展結構水平.

(3)單點結構的求導,常考多點結構單調性,最值,零點.

(4)題目綜合性較強,融合關聯多個單點結構知識點.

3 運用SOLO 分類理論進行導數解答題復習教學案例分析與探討

SOLO 分類理論在國內教育中已經有了一些廣泛的應用,主要集中在分析學習結果及學習障礙、試題編制、制定評分標準以及指導教學設計方面.筆者在前人基礎上在2023年高考復習中也做了一些實踐,有一些切身感悟.以下以筆者分析2023 年廣州市二模第22 題后進行的教學實踐為例進行闡述.

題目: (2023 年廣州市二模第22 題) 已知函數f(x) =ln(1+x),g(x) =ax2+x.(1) 當x＞-1 時,f(x) ≤g(x), 求實數a的取值范圍; (2) 已知n∈ N*, 證明:.

這一題學生的作答有一些共性, 為方便表述, 我做以下編號: ①構造函數h(x) =x- ln(x+1), 證明x＞-1 時,x＞ln(x+1),從而a≥0 時,結論成立.②當a＜0 時, 取一個點使得結論不成立, 比如取,此時f(x0)＞g(x0), 結論不成立.③f(0) =g(0); 當x0 時參變分離后構造函數,求出.④構造函數G(x) =x2+2x-2(x+1)ln(x+1), 發現G(0) = 0, 判斷G(x)的單調性,求出范圍;得到F(x)的單調性,運用洛必達法則求出F(x) 的范圍.⑤聯想到當a= 0 時, 由(1)得ln(x+1) ≤x, 則lnx≤x-1, 可得, 即, 即所以,, 又有, 即, 所以,k∈{0,1,2,··· ,n}.⑥構造函數s(x) =x-sinx(x＞0),求最值證明sinx＜x(x＞0).

3.1 運用SOLO 分類理論分析學生的作答,由單點結構到更高層次結構,由部分到整體,能夠更清晰準確了解學生知識點的掌握情況和思維層次.

考完之后筆者對學生的作答運用SOLO 分類理論分析并進行了整理統計,分析學生的學習情況,得到表3.

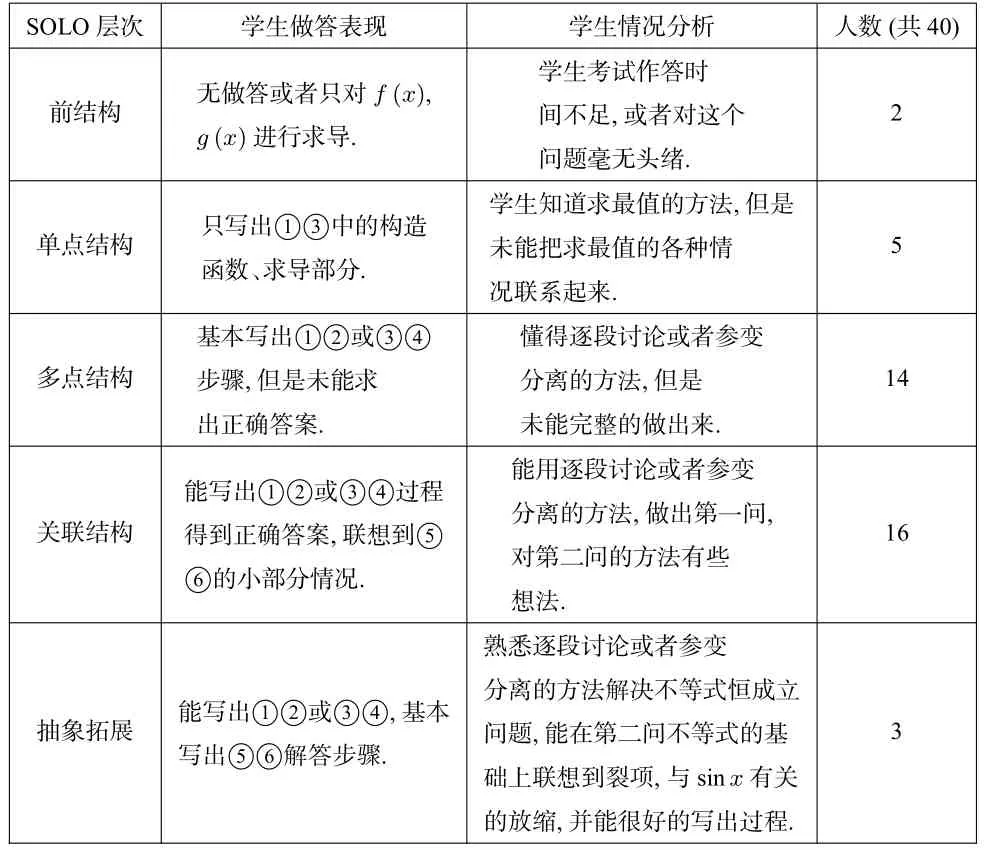
表3 學生作答情況統計分析

從表3 中,可以了解到: (1)班級同學基本都懂得使用逐段討論的方法或者參變分離的方法證明不等式恒成立問題.能夠把單點結構求導、單調性、最值聯系起來,學生的水平基本上達到了多點結構、關聯結構水平.(2)學生在運用逐段討論、參變分離解決不等式恒成立的通性通法時,思維還需要深化,速度還需要提升,需要促進大部分學生達到關聯結構水平.(3)大部分學生未能達到抽象拓展結構水平,在第二問中未能聯想到與sinx有關的放縮,未能想到裂項相消的方法.(4)學生在考試中做導數解答題的意識較強.

3.2 運用分類理論進行教學設計,把高層次結構的題目分解為低層次結構的題目,化繁為簡;從單點結構,再到更深層次結構遞進,循序漸進,使得思維有了梯度,更好的促進學生的思維發展.

針對二模導數題的解答, 筆者設計了以下練習題:1.當a≥0 時, 求函數t(x) =ax2+x- ln(x+1) 在x＞-1 范圍內的最小值.2.當x＞-1 且x0 時, 求函數的取值范圍.3.當x＞-1時, ln(x+1) ≤ax2+x, 求實數a的取值范圍.4.證明: 當x＞0 時,x＞sinx恒成立.5.證明: 當x＞1時,恒成立.6.已知當n∈N*時, 證明:.

設計意圖: 第1 題為學生使用逐段討論的方法做鋪墊.第2 題為學生使用參變分離的方法做鋪墊.第3 題再在前2題的情況下解決不等式恒成立問題.這樣的設計給思維方法設置了梯度,學生的思維自然的從單點結構到多點結構再到關聯結構逐步發展.第4 題是一個關于放縮的不等式.第5題是為了裂項做準備.在前2 題的鋪墊下,再來解決第6 題更是讓思維有了連接點,結構之間更容易銜接在一起.學生的思維也能從單點結構到多點結構再到關聯結構抽象拓展結構逐步發展.

3.3 運用SOLO 分類理論對學生進行過程性評價,能夠更全面細致的評價學生的知識點掌握情況,尤其是能看到一些低層次的思維結構的閃光點,提升學生自我效能感.

在以上題目中,能夠完整,規范的寫出整個題的解答的同學非常之少,如果只以結果作為評價,將會打擊到大部分同學的自信心,也不能客觀公正的評價學生作答情況,根據SOLO 分類理論把高層次結構分解為低層次結構,對每位同學在低層次結構問題上的作答進行評價,是客觀的過程性評價.有助于學生發現自己的閃光點,獲得信心,從而在考試中學生也會有意識的留出時間對導數進行作答,實現分步得分的策略.

3.4 運用SOLO 分類理論進行教學,從單點到多點,多點到關聯,關聯到抽象拓展,有助于學生理清知識脈絡,規范作答,踩點得分,提高效率.

在以上題目中, 第一問在第1 題的引導下以及講解了①②后, 學生很清晰的掌握逐段討論的解題步驟, 也能深刻理解難點在于舉出反例.在第2 題的引導下以及講解了③④后,學生能清晰的掌握參變分離法的解題步驟,也能體會到難點在于求函數的最值.第二問中在第4、5 題的鋪墊下,兩個放縮,再到裂項相消,學生從正弦函數的放縮,再到裂項相消的構造,思路清晰,脈絡清楚.在這個過程中層層相扣,能夠促進學生嚴謹規范作答.學生在聽課上也能夠有側重的聽課,提高效率.

4 結束語

SOLO 分類理論對學生的思維水平做了細分,為教學提供了理論依據.導數解答題綜合性強、思維跨度大,在復習中,老師、學生容易陷入困境.SOLO 分類理論正好為我們的教-學-評提供了有效的依據.以上為筆者在教學中的一點實踐探索,希望能引起共鳴.