對一道圓錐曲線問題的探究與拓廣
郭永生
? 山東省菏澤市定陶區第一中學
一套成功的試卷總是不乏好題,立意新穎,典型突出,亮點十足,引人注目.這類試題往往知識融合自然,考點科學交匯,具有良好的教研價值,倍受眾多數學愛好者青睞,非常值得我們深入思考、分析與探究.
1 問題呈現
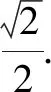
(1)求軌跡E的方程.
(2)設過點A(0,-1)且斜率為k1的動直線與軌跡E交于C,D兩點,且點B(0,2),直線BC,BD分別交圓x2+(y-1)2=1于異于點B的點P,Q,設直線PQ的斜率為k2,問是否存在實數λ,使得k2=λk1成立?若存在,求出λ的值;若不存在,請說明理由.
2 問題解答
上述問題的解答如下.
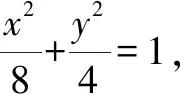
(2)由題意知,直線CD的方程為y=k1x-1.設C(x1,k1x1-1),D(x2,k1x2-1).
將y=k1x-1與x2+2y2-8=0聯立,消去y,得
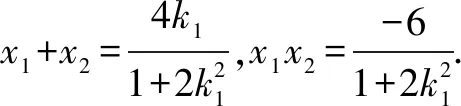
設直線PQ的方程為y=k2x+m,P(x3,k2x3+m),Q(x4,k2x4+m).
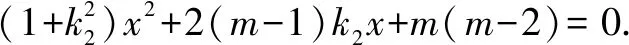
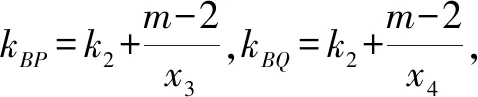
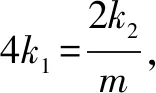
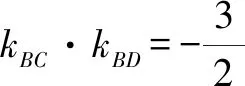
3 問題探究
經過初步探究,發現:
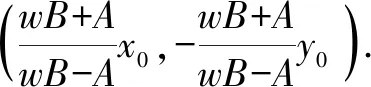
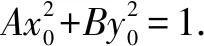
設M(dy1+t,y1),N(dy2+t,y2),則
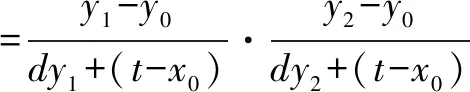
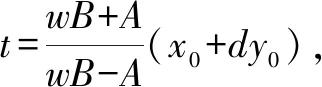
特別地,可得以下結論:
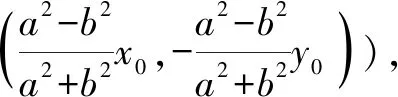
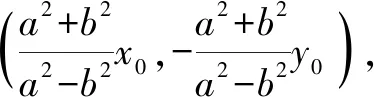
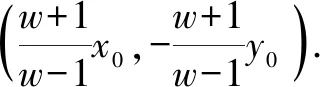
當TM⊥TN時,則直線AB恒過點(0,0).
(注:上述e為相應曲線的離心率.)
4 拓廣探索
再進一步深入研究拋物線,發現類似性質:
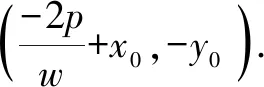
特別地:
(1)當TM⊥TN時,時,直線MN恒過定點(2p+x0,-y0);
(2)當x0=y0=0,且TM⊥TN時,直線MN恒過定點(2p,0).
5 鏈接高考
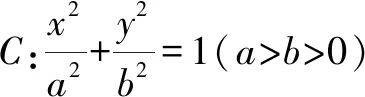
(1)求C的方程;
(2)點M,N在C上,且AM⊥AN,AD⊥MN,D為垂足.證明:存在定點Q,使得|DQ|為定值.
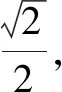
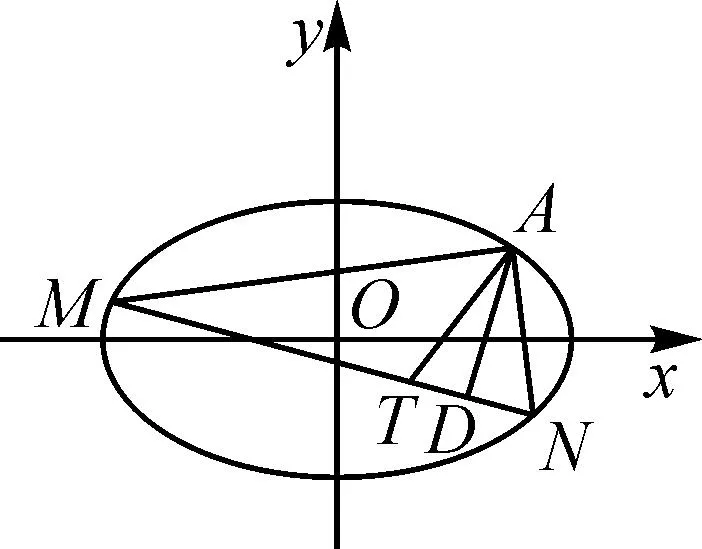
圖1

當下高中數學教學面臨新教材、新課程、新高考所引領的三新環境,單純從學科教與學的角度來看,學習探究應該成為適應新時代下教與學的新常態,特別是像學習圓錐曲線等一類難度較大的內容時,教師更有必要下功夫思考與探究.圓錐曲線的性質十分豐富,可供探究的方面十分廣泛,以上筆者所探討的這些只不過是圓錐曲線性質中的冰山一角,滄海一粟,期盼早日見到新時代同行們更多、更好的教學研究成果,以期同學習、共進步!Z

