RMI視角下高中數(shù)學(xué)教學(xué)的“四化”

姜衛(wèi)東

? 江蘇省揚(yáng)州中學(xué)

關(guān)系映射反演法則(簡(jiǎn)稱RMI法則)作為數(shù)學(xué)方法論中的一種重要法則[1],一般可以表述如下:給定一個(gè)目標(biāo)原象x的關(guān)系結(jié)構(gòu)S,如果能找到一個(gè)映射φ,將S映入或映滿S*,則可從S*通過一定的數(shù)學(xué)方法把目標(biāo)映象x*=φ(x)確定出來,進(jìn)而通過反演φ-1又可以把x=φ-1(x*)確定出來,這樣原來的問題就得到解決.利用RMI法則解決問題的過程可用框圖1表示如下:

RMI法則不僅對(duì)數(shù)學(xué)科學(xué)的發(fā)展起過推動(dòng)作用,而且對(duì)高中數(shù)學(xué)教學(xué)也有著指導(dǎo)意義.在平時(shí)的教學(xué)工作中,如能從RMI的視角來審視高中數(shù)學(xué)教學(xué),定會(huì)優(yōu)化解題教學(xué)、深化教材理解、強(qiáng)化大單元整體教學(xué)及催化創(chuàng)新思維等,在提高教學(xué)效益的同時(shí),進(jìn)一步提升學(xué)生的數(shù)學(xué)思維能力與學(xué)科核心素養(yǎng).

1 RMI視角下,解題教學(xué)的優(yōu)化

數(shù)學(xué)解題有各種不同的方法,所有這些方法,其實(shí)就是RMI法則在解題中的具體運(yùn)用,只不過不同的方法對(duì)應(yīng)的映射φ不同而已.特別是在處理一些難度較大的試題時(shí),如能巧妙地利用RMI法則,有時(shí)能起到事半功倍的效果.

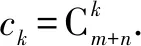
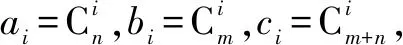
而要求解的問題x便是ck=?

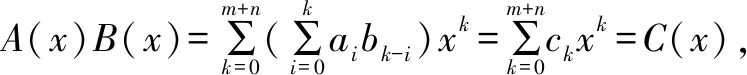
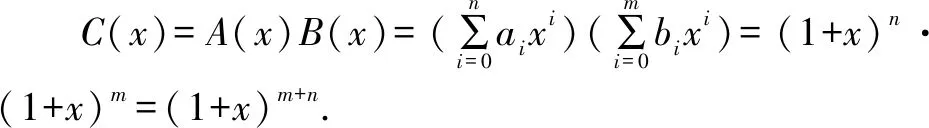
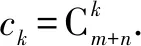
由上可知,利用RMI法則解題的關(guān)鍵在于選擇適當(dāng)?shù)挠成涔ぞ擀占胺囱莨ぞ擀?1,將需求解問題x與其映象x*進(jìn)行轉(zhuǎn)換.因此,在后續(xù)的論述中,筆者將注重對(duì)φ及φ-1的分析,而不嚴(yán)格按照上面的五個(gè)步驟進(jìn)行.

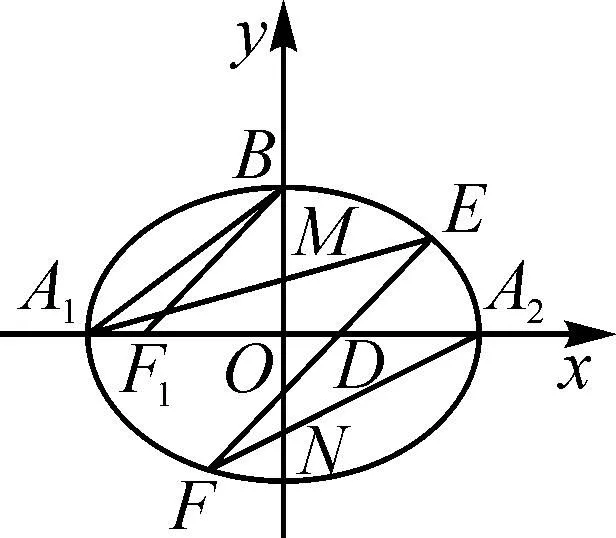
圖2

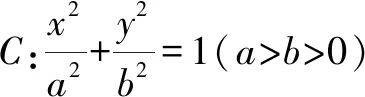
(1)求橢圓C的方程;

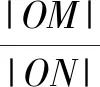
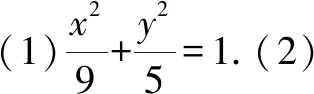
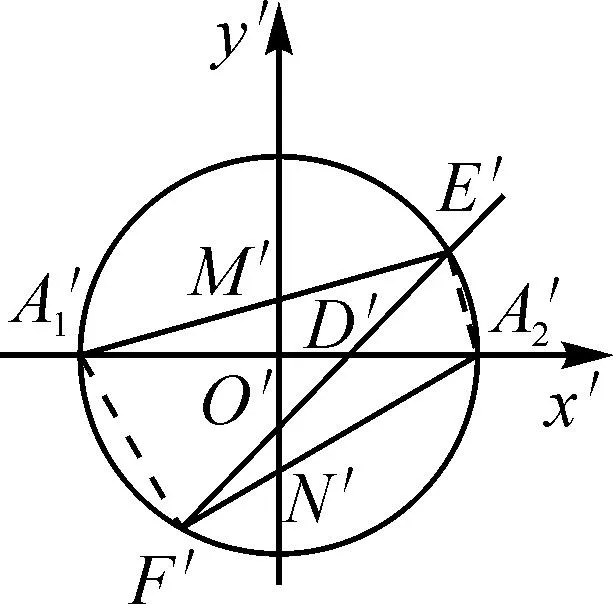
圖3

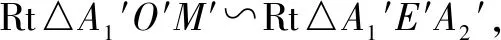
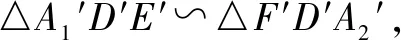
上述解法就是RMI法則的具體運(yùn)用,它的解題過程可用框圖4表示如下.

需要指出的是,在解決同一個(gè)問題時(shí),選擇不同的映射φ,就會(huì)出現(xiàn)不同的解法.因此,要得到問題的簡(jiǎn)解,應(yīng)根據(jù)不同的問題背景,靈活選擇φ.

2 RMI視角下,教材理解的深化

盡管在高中數(shù)學(xué)教材中并未明確地提及RMI法則,但是它的方法與內(nèi)容一直以不同的水準(zhǔn)被隱含在數(shù)學(xué)教材及教學(xué)活動(dòng)中,教師只有經(jīng)過分析觀察,才能把它抽象出來,進(jìn)而更加有效地組織教學(xué).

案例2-1指數(shù)函數(shù)與對(duì)數(shù)函數(shù).

在蘇教版必修一教材中,對(duì)數(shù)函數(shù)的知識(shí)是安排在指數(shù)函數(shù)之后的,在學(xué)完指數(shù)函數(shù)的概念、圖象及性質(zhì)以后,如何組織對(duì)數(shù)函數(shù)的學(xué)習(xí),實(shí)際上體現(xiàn)了教師對(duì)教材編寫意圖的理解.

筆者以為,教材將這兩類函數(shù)放在一起學(xué)習(xí),正是關(guān)注了它們之間的緊密聯(lián)系,其本質(zhì)就是RMI法則的體現(xiàn)!這里S可看成是對(duì)數(shù)函數(shù)的結(jié)構(gòu)體系,是待研究的內(nèi)容.引入映射φ:求反函數(shù),在φ的作用下,對(duì)數(shù)函數(shù)就映射成指數(shù)函數(shù),而指數(shù)函數(shù)的知識(shí)結(jié)構(gòu)S*(圖象及性質(zhì)等)已經(jīng)研究清楚了,所以只需根據(jù)φ-1:求反函數(shù),反演回去,就可以得到對(duì)數(shù)函數(shù)的圖象及性質(zhì)等(即S).當(dāng)然,這里φ與φ-1也可以從形上來構(gòu)造,那就是作關(guān)于y=x對(duì)稱的圖象,它們的關(guān)系可以用下面的框圖5表示.

由上可知,指數(shù)函數(shù)與對(duì)數(shù)函數(shù)是彼此依存的統(tǒng)一體,了解這一點(diǎn),對(duì)于課堂教學(xué)的組織以及知識(shí)的建構(gòu)都大有裨益!

案例2-2數(shù)學(xué)建模.

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017年版2020年修訂)》提出了數(shù)學(xué)學(xué)科六大核心素養(yǎng)以及貫穿高中數(shù)學(xué)課程的四條主線[2],數(shù)學(xué)建模是其中之一,而且在每?jī)?cè)教材中,都有數(shù)學(xué)建模的專題.毋庸諱言,在教學(xué)實(shí)踐中,數(shù)學(xué)建模教學(xué)的開展并不盡如人意,其中的原因固然是多方面的,但教師自身的觀念與數(shù)學(xué)建模能力是制約當(dāng)下數(shù)學(xué)建模教學(xué)的關(guān)鍵因素.

而要提升教師的數(shù)學(xué)建模素養(yǎng),建立關(guān)于數(shù)學(xué)建模的正確觀念,就必須從RMI法則的視角來了解數(shù)學(xué)建模,這里S是指現(xiàn)實(shí)問題,φ就是通過化簡(jiǎn)、假設(shè)等方法進(jìn)行抽象,S*就是抽象出來的數(shù)學(xué)模型,反演工具φ-1就是將數(shù)學(xué)模型的解進(jìn)行解釋或翻譯,從而解決現(xiàn)實(shí)問題.

因此,數(shù)學(xué)建模不是有些人所認(rèn)為的就是解應(yīng)用題,它遠(yuǎn)比解應(yīng)用題復(fù)雜得多.究其本質(zhì)而言,數(shù)學(xué)建模實(shí)際上就是RMI法則中一種重要的類型——概念映射法(抽象分析法),它的過程可用框圖6表示如下:

3 RMI視角下,大單元整體教學(xué)的強(qiáng)化

在新課改的大背景下,高中數(shù)學(xué)教學(xué)的根本任務(wù)是培養(yǎng)學(xué)生的數(shù)學(xué)思維能力與學(xué)科核心素養(yǎng).因此,在平時(shí)的教學(xué)中,必須著眼于幫助學(xué)生建立起完整的、系統(tǒng)化的知識(shí)體系,促進(jìn)學(xué)生對(duì)數(shù)學(xué)知識(shí)的整體化認(rèn)知,避免所學(xué)知識(shí)碎片化與零散化.所以,教師需在仔細(xì)分析新課標(biāo)、新教材、教學(xué)重難點(diǎn)及教學(xué)方法等教學(xué)要素的基礎(chǔ)上,深刻把握單元知識(shí),抓住內(nèi)容主線,厘清知識(shí)的關(guān)聯(lián),積極開展大單元整體教學(xué),從而有效促進(jìn)學(xué)生的深度學(xué)習(xí)及高階思維能力的發(fā)展.筆者以為RMI法則是實(shí)施大單元整體教學(xué)的一種重要手段,它可以強(qiáng)化這種教學(xué)方式的落實(shí)與實(shí)施.

案例3-1解析幾何的大單元教學(xué).

蘇教版選擇性必修一中第1章、第2章及第3章(直線、圓、圓錐曲線與方程)構(gòu)成了解析幾何的一個(gè)大單元,完全可以實(shí)施大單元整體教學(xué),它們的RMI法則幾乎是一致的.這里原象關(guān)系結(jié)構(gòu)S就是曲線及其性質(zhì),建系后,映射φ:點(diǎn)→坐標(biāo),曲線→方程,映象關(guān)系結(jié)構(gòu)S*:方程及其關(guān)系,φ-1:坐標(biāo)→點(diǎn),方程→曲線,從而由方程(組)的解的情況,反演推出曲線的幾何性質(zhì)及位置關(guān)系.通過RMI法則,學(xué)生不僅能清晰地理解處理曲線與方程的解析法思想,而且能了解處理直線、圓及圓錐曲線問題的一致性,以利于學(xué)生對(duì)解析幾何的整體把握.

案例3-2平面向量與空間向量的大單元教學(xué).

盡管平面向量與空間向量分屬于蘇教版必修二第9章和選擇性必修二第6章,但是也可以利用RMI法則進(jìn)行大單元教學(xué).它們的RMI法則基本一致.這里S是指(平面或空間)向量及其關(guān)系、運(yùn)算,建系后,映射φ:向量→坐標(biāo),這時(shí)S*:實(shí)數(shù)(坐標(biāo))運(yùn)算及其關(guān)系,通過φ-1:坐標(biāo)→向量,反演推出向量的運(yùn)算及位置關(guān)系.以上RMI法則,不僅可以讓學(xué)生理解研究(平面或空間)向量的坐標(biāo)法思想,而且能夠深刻地揭示向量所具有的數(shù)與形兩個(gè)方面的特征,因而向量是溝通代數(shù)、幾何與三角函數(shù)的紐帶,為解決平面及空間圖形的位置關(guān)系及度量問題提供了十分有效的工具.這無疑對(duì)學(xué)生整體建構(gòu)向量知識(shí)體系,領(lǐng)會(huì)知識(shí)本質(zhì)是有益的!

實(shí)際上,對(duì)于案例3-1及3-2,我們還可以在更大范疇下進(jìn)行整體教學(xué).無論是曲線還是向量,它們都是數(shù)學(xué)中要研究的對(duì)象,要研究的都是數(shù)學(xué)對(duì)象及其關(guān)系、性質(zhì)等,采用的映射工具,都是建系后得到它們的坐標(biāo)或方程,所以案例3-1與3-2,還可以用以下統(tǒng)一的框圖7來表示.

這樣,學(xué)生就能從宏觀上更深刻地理解數(shù)學(xué)是研究數(shù)量關(guān)系與空間形式的科學(xué)、數(shù)學(xué)所具有的數(shù)形特征及研究通法.

4 RMI視角下,創(chuàng)新思維的催化

培養(yǎng)數(shù)學(xué)創(chuàng)新思維是當(dāng)今數(shù)學(xué)教育的重要使命與時(shí)代呼喚.盡管大家對(duì)培養(yǎng)學(xué)生創(chuàng)新思維的重要性與緊迫性已達(dá)成共識(shí),但對(duì)培養(yǎng)學(xué)生創(chuàng)新思維的教學(xué)策略還有所欠缺.筆者以為RMI法則是催化學(xué)生創(chuàng)新思維的一個(gè)重要策略,可以挖掘數(shù)學(xué)史中數(shù)學(xué)發(fā)現(xiàn)與發(fā)明中的RMI法則對(duì)學(xué)生進(jìn)行創(chuàng)新思維的培育,也可以通過開展研究性學(xué)習(xí)的方式,讓學(xué)生親歷運(yùn)用RMI法則進(jìn)行“再發(fā)現(xiàn)”“再創(chuàng)造”的歷程.

案例4解析幾何的發(fā)現(xiàn).

解析幾何是十七世紀(jì)前半葉產(chǎn)生的一個(gè)嶄新的數(shù)學(xué)分支,從本質(zhì)上來看,它的發(fā)現(xiàn)過程就是RMI法則的具體應(yīng)用.坐標(biāo)法的建立使點(diǎn)與有序?qū)崝?shù)對(duì)之間、曲線與方程之間建立對(duì)應(yīng)關(guān)系,從而把研究曲線的幾何問題轉(zhuǎn)化為研究方程的代數(shù)問題,通過對(duì)方程的討論來研究曲線的幾何性質(zhì),這一過程可用框圖8表示如下.

通過解析幾何發(fā)展史的介紹,學(xué)生明白數(shù)學(xué)知識(shí)的發(fā)現(xiàn)與創(chuàng)造并不是憑空產(chǎn)生的,而是有規(guī)律可循的,RMI法則在其中就扮演著重要的角色!數(shù)學(xué)家可以利用RMI法則創(chuàng)造數(shù)學(xué),教師也能夠在平時(shí)的教學(xué)實(shí)踐中,鼓勵(lì)學(xué)生運(yùn)用RMI法則體驗(yàn)“數(shù)學(xué)發(fā)現(xiàn)與創(chuàng)造”的樂趣.

在一次研究性學(xué)習(xí)中,筆者跟學(xué)生介紹了RMI法則后,讓學(xué)生嘗試運(yùn)用RMI法則自主編制習(xí)題、提出問題.其中一個(gè)學(xué)生結(jié)合伸壓變換的性質(zhì),編制了一道較高質(zhì)量的試題,其編制過程如下:

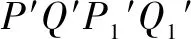
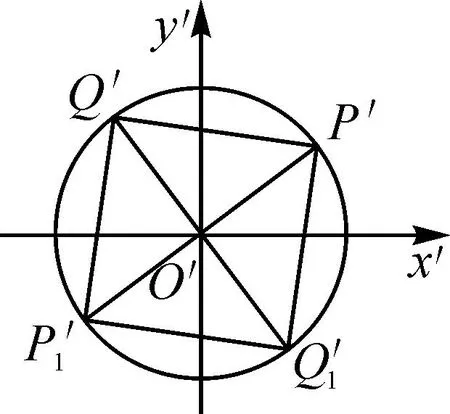
圖9

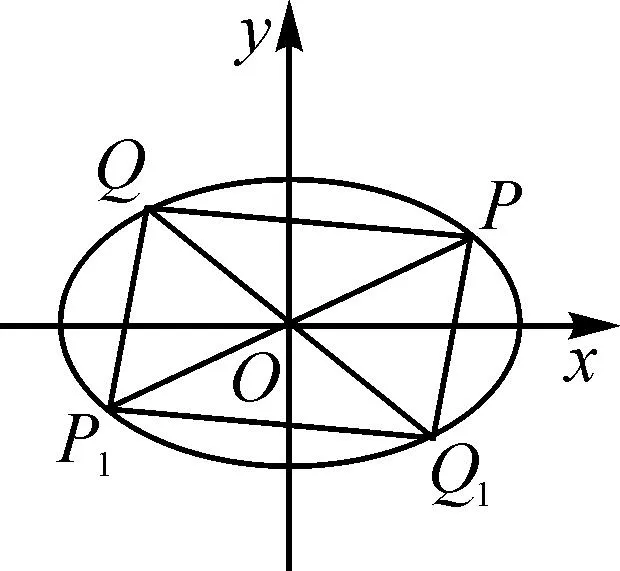
圖10

在教師的引導(dǎo)下,學(xué)生對(duì)試題進(jìn)行了包裝:橢圓的標(biāo)準(zhǔn)方程不直接給出,而是由焦點(diǎn)坐標(biāo)與準(zhǔn)線方程來確定.這樣一道完整的橢圓原創(chuàng)題就新鮮出爐了:

已知橢圓的中心在坐標(biāo)原點(diǎn),左焦點(diǎn)為F1(-1,0),右準(zhǔn)線方程為x=4.

(1)求橢圓的標(biāo)準(zhǔn)方程;

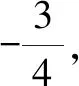
以上應(yīng)用RMI法則編題的過程可用框圖11來表示.

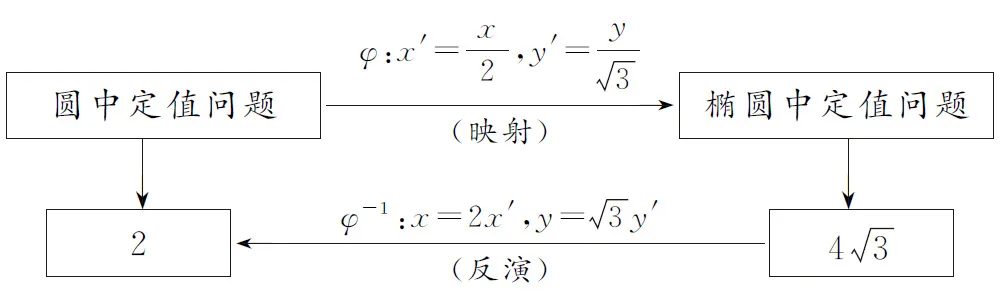
圖11

通過這次研究性學(xué)習(xí),學(xué)生都驚詫于自己的表現(xiàn),他們不僅發(fā)現(xiàn)了RMI法則的巨大作用,更體會(huì)了“數(shù)學(xué)發(fā)現(xiàn)與創(chuàng)造”的樂趣,實(shí)現(xiàn)了從“問題解決者”到“問題發(fā)現(xiàn)者”“問題提出者”的轉(zhuǎn)變.這正是新課標(biāo)所倡導(dǎo)的理念,也是落實(shí)數(shù)學(xué)核心素養(yǎng)的根本遵循!