解三角形中的最值或范圍問題

李鴻媛

? 哈爾濱師范大學教師教育學院

1 與邊有關的最值或范圍問題

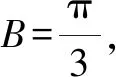
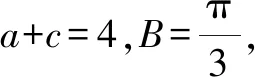
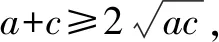
評析：本題利用已知條件結合余弦定理,借助基本不等式求三角形邊的取值范圍[1],滲透了邏輯推理、數學運算等數學核心素養.

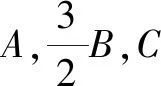
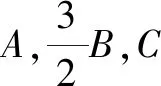
評析：本題考查了學生對等差數列的概念、三角形內角和定理、三角形面積公式、余弦定理等的掌握情況.解題的關鍵是將余弦定理與不等式相結合,進而求出三角形一邊的最值.

2 與角有關的最值或范圍問題

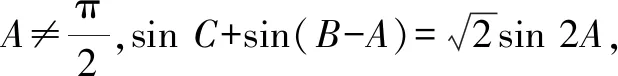
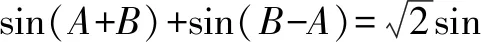
評析：解法一利用三角形內角和定理、兩角和與差的正弦公式、正弦定理與三角函數的性質等知識,對學生的推理能力、運算能力和直觀想象能力進行了考查.

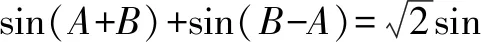
評析：解法二考查了三角形內角和定理、兩角和與差的正弦公式、正弦定理、余弦定理、基本不等式等知識.這種解題方法需要學生靈活運用兩個正數的和與積的關系,充分體現學生的數學運算能力和數據分析能力.

3 與周長有關的最值或范圍問題

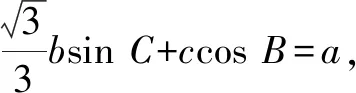
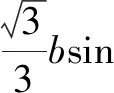
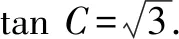
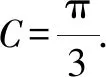
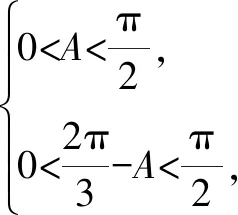
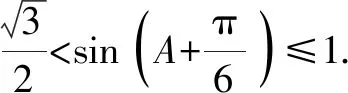
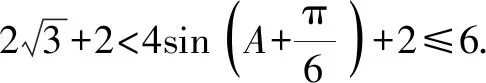
因此△ABC周長的最大值為6.

評析：這道題解題的關鍵是利用正弦定理將邊化為角,轉化為求三角函數的最值問題[2],考查了邏輯推理和數學運算等核心素養.

4 與面積有關的最值或范圍問題

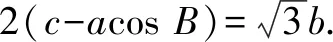
(1)求角A;

(2)若a=2,求△ABC面積的取值范圍.

解法一：(1)略.

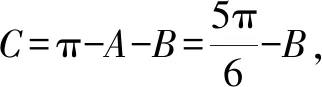
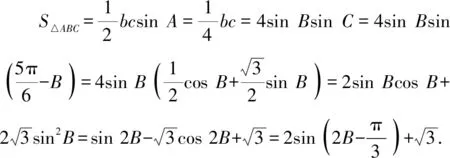
解法二：(1)略.

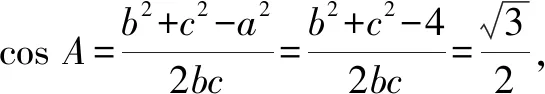
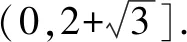
數學這門學科需要學生具備較強的邏輯推理能力、運算能力、直觀想象能力等.針對解三角形最值或范圍問題,學生需要熟練掌握三角形的面積公式、同角三角函數的基本關系、正弦定理、余弦定理、基本不等式等知識,并能夠進行綜合運用.