基于表面效應三維納米多孔金屬力學性能的有限元分析1)

張永超 糜長穩 茍曉凡 ,3)

* (河海大學力學與材料學院,南京 211100)

? (東南大學土木工程學院,南京 211102)

引言

近10 年來,伴隨著先進增材制造技術的快速發展,納米多孔金屬代表著多孔金屬材料極端形態,兼具傳統多孔結構和納米金屬材料的雙重特性,受到廣泛地關注[1-4].納米多孔金屬不僅具有高孔隙率和高比表面積的結構特點,在表面效應的作用下,還具備異于傳統多孔金屬的力學性能[5-7].因此,針對納米多孔金屬材料,結合微結構表面效應,探究模型參數與力學性能的影響規律,具有重要的工程實際意義.

納米多孔金屬材料力學性能的研究與納米表面理論發展密切相關,最早可以追溯到Gibbs[8]的開創性工作.為在力學框架內衡量表面效應,Gurtin 和Murdoch 等[9-10]將納米表面視作一層能夠承受面內拉伸的零厚度薄膜,并建立了考慮表面拉伸剛度的表面彈性模型.此后,針對不同形式的納米多孔金屬材料,微結構表面效應的影響研究逐漸發展起來.按結構的維度次序,Feng 等[11]較早地將表面效應引入一維納米梁,結合歐拉-伯努利梁理論,提出可預測開孔納米多孔金屬材料有效楊氏模量的微觀力學模型.Dai 等[12]和He 等[13]分別討論了遠場載荷作用下二維彈性平面和三維彈性介質中納米孔洞附近的應力集中效應.Wang 等[14]則研究了兩個具有表面張力的納米橢圓孔間的相互作用.

分子動力學方法可通過追蹤原子相互作用來捕捉納米材料微結構表面效應[15-20].對特征尺寸處于幾十納米以內的多孔金屬材料,分子動力學方法被證明具有一定的指導作用,但當結構尺寸上升至幾百納米甚至更高時,分子動力學方法的計算成本急劇增加,計算效率也顯著降低[21-22].值得慶幸的是,在合理網格密度前提下,基于連續介質力學基本原理的有限元法,其計算效率并不明顯受到制造工藝、結構建模和模型尺寸等因素的約束[23-26].然而,傳統有限元方法因尚不具備模擬納米尺度下材料和結構力學行為的公式體系,因此難以精準捕捉納米材料微結構表面效應[27-28].

盡管如此,依然有部分學者通過為孔洞表面定制有限單元的方式,嘗試捕捉納米孔洞表面力學響應.二維納米孔洞表面可離散為一維單元,因此,Gao等[29]在傳統有限元程序中引入一維表面單元,并以此研究了二維納米多孔金屬材料力學性能.Wang 等[30]采用與Gao 等[29]類似的方法,討論了二維納米圓孔附近應力集中現象,不同的是,他們通過用戶單元二次開發,進一步將所開發的一維納米單元植入商用有限元軟件.通過以上分析可以發現,以往采用有限元方法對納米多孔金屬力學性能的研究,將計算模型簡化為較為簡單的二維結構,因此無法真實刻畫納米多孔金屬材料的力學特性.截至目前,通過直接定制表面單元的方式來捕捉三維納米多孔金屬表面效應的研究還未見報道,依然缺乏針對一般三維納米多孔金屬結構的計算模型和分析方法.

據此,本文基于能量最小原理,將Gurtin-Murdoch表面模型引入單元剛度矩陣和單元平衡方程,通過為納米表面構建有限元單元的方式,結合微觀模型非均勻性,構建針對一般三維納米多孔金屬力學性能的有限元模型.采用所開發的計算模型,揭示孔隙率、孔洞數量和表面參數等因素對楊氏模量、壓縮屈服強度和吸能性等力學性能的影響規律,為納米多孔金屬的材料制備和力學性能預測提供科學依據.

1 納米多孔金屬有限元模型

1.1 系統能量方程

考慮包含任意形狀納米孔洞的彈性體V,其中,Ω代表納米孔洞區域,Γ=?? 代表納米孔洞邊界.假設彈性體V受體力b的作用,在彈性體外邊界St上受面力t的作用,如圖1 所示,則基體材料應變能UB、表面彈性能US、外力做功W和彈性系統的總能量П滿足

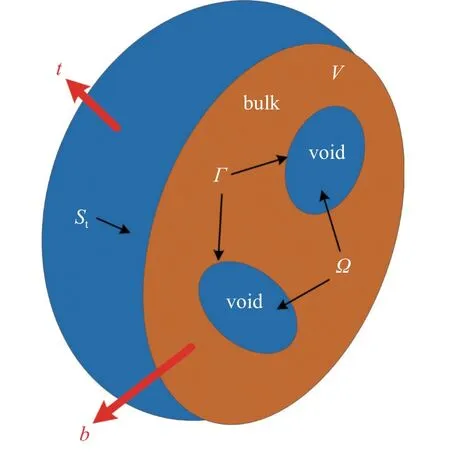
圖1 包含任意形狀納米孔洞的彈性體力學模型Fig.1 Mechanical model of elastomer containing arbitrarily shaped nanoholes

其中,u表示外力作用引起的位移張量,γB和γS分別表示基體應變能密度和表面彈性能密度.彈性基體應變能密度和Gurtin-Murdoch 表面模型[9]定義的表面彈性能密度分別為

其中,γ0為表面自由能密度,εB,εS和τS分別為基體應變、表面應變和表面殘余應力張量,DB和DS分別為基體和表面彈性剛度張量.

對式(1)進行變分后根據能量最小原理可得

將式(3)帶入式(2)后進行變分,可得基體應變能、表面彈性能和外力做功的變分式

1.2 單元平衡方程

為刻畫表面效應,對納米多孔金屬表面定制有限元單元.其中,基體單元的位移uB、應變 εB和表面單元的位移uS和應變 εS可分別表示為

其中,NB和NS分別為基體單元和表面單元的形函數,BB和BS分別為基體單元和表面單元的應變矩陣,分別為基體單元和表面單元節點位移.在孔洞表面,基體單元與表面單元的節點位移之間滿足

其中,T為坐標轉換矩陣,可將單元節點位移由全局坐標轉換為局部坐標.將式(5)～式(8)代入式(4),可以得到系統能量方程的有限元格式

因此,離散系統的單元平衡方程可表示為

對于基體單元滿足:c1=1,c2=0;對于表面單元滿足:c1=0,c2=1.式(10)表示的單元平衡方程由基體單元剛度矩陣、表面單元剛度矩陣和單元節點力f3 個部分組成.其中,表面單元剛度矩陣部分包含表面彈性剛度DS的貢獻,而表面殘余應力(Gurtin-Murdoch 表面本構模型中應變無關項的表面殘余應力)則與體力和面力一同被包含進單元節點力部分.因此,只要分別對基體和表面制定合適的單元,按式(11)計算出基體單元剛度矩陣、表面單元剛度矩陣和單元節點力f,再帶入系統單元平衡方程進行迭代,即可計算出納米表面力學響應.

1.3 表面單元定制

對于基體材料,ABAQUS 內置了豐富的體單元類型,因此不需要進行特別定制.三維納米多孔金屬的孔洞表面經離散后可視作二維單元,由式(11)可知,Gurtin-Murdoch 表面模型將納米表面視為一層能夠承受拉伸的零厚度薄膜,因此變形模式與二維面單元類似.經常使用的二維面單元有3 節點單元和四節點單元.其中,4 節點單元計算精度較高,3 節點單元則對復雜邊界具有較強的適應能力,同時也更有利于有限元計算的快速收斂,可以達到節約計算成本的目的,因此,本文以3 節點三角形面單元為基礎,來對Gurtin-Murdoch 型納米表面進行離散,基體材料則采用四面體單元進行離散.如圖2(a)所示,3 節點三角形面單元的i,j和k節點分別與4 節點四面體單元的I,J和K節點互為共有節點.

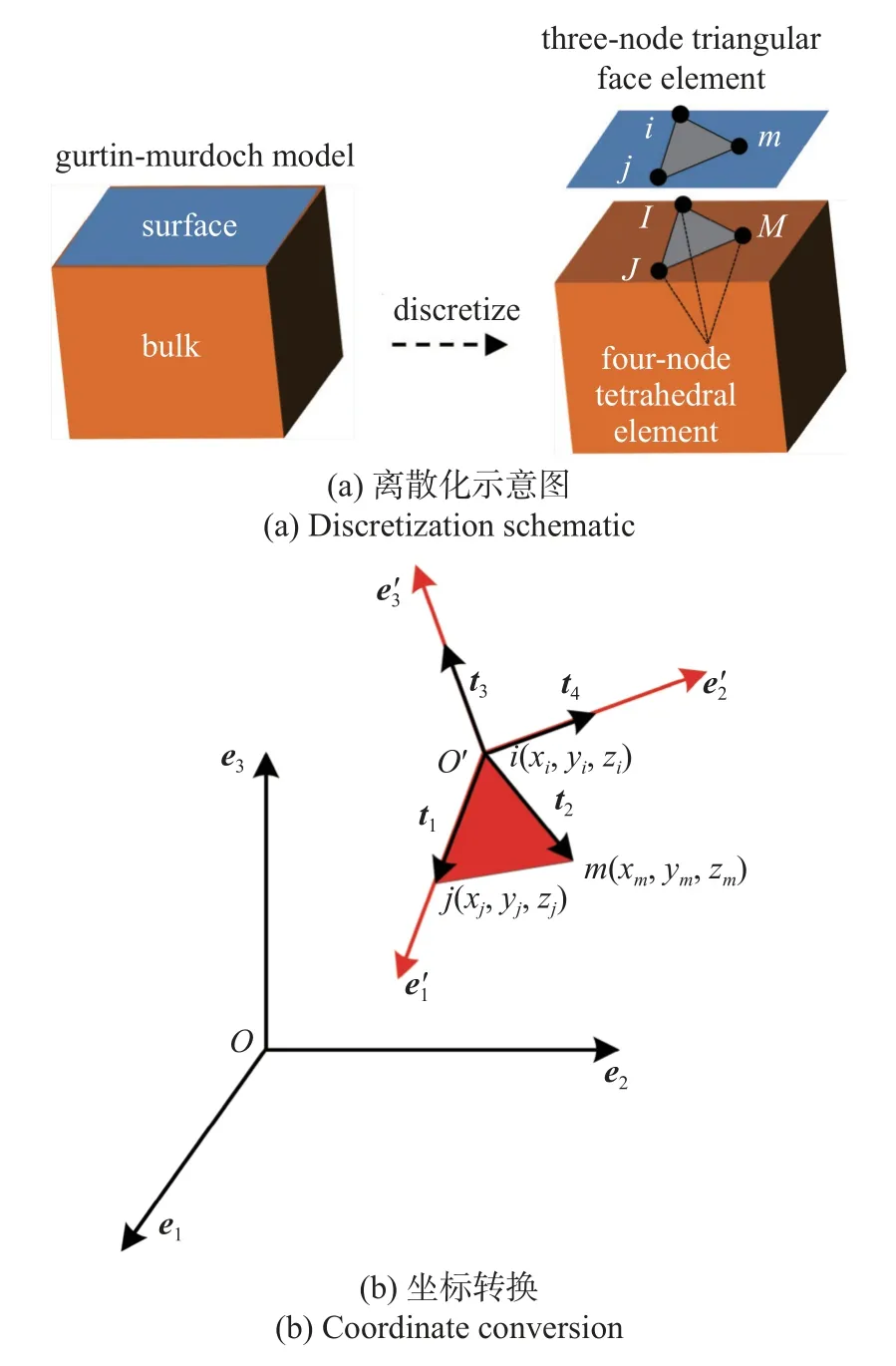
圖2 表面單元和基體單元Fig.2 Surface element and bulk element

3 節點三角形面單元是二維單元,在利用FORTRAN語言對ABAQUS 進行二次開發時,可直接獲取有限元系統全局坐標系下表面單元節點坐標,但無法直接獲取局部坐標系下表面單元節點坐標,因此可分三步對表面單元進行定制:

(1) 將全局坐標系下表面單元節點坐標轉換到局部坐標系中;

(2) 在局部坐標系下推導表面單元應變矩陣和單元剛度矩陣;

(3) 將局部坐標下應變矩陣和單元剛度矩陣轉換到全局坐標系中,建立表面參數和單元參數關聯機制,實現表面單元與三維基體單元的數據交換.

將全局坐標系下的單元節點坐標代入式(12),可以得到投影ars,隨后根據式(13)(坐標轉換方程)可得3 節點三角形面單元在局部坐標系下的節點坐標值.

其中,a1,a2和a3分別為局部坐標系原點O′在全局坐標系下的坐標.

在局部坐標系和全局坐標系下,3 節點三角形面單元的單元節點位移可分別表示為

二者之間滿足坐標轉換關系

其中,坐標轉換矩陣滿足

需要指出的是,在孔洞表面處,全局坐標系下表面單元節點位移和基體單元節點位移滿足:對3 節點三角形面單元的應變矩陣在空間中進行擴充可得

其中,單元面積Atri為

常數bi和ci為

式中的 (i,j,m) 表示下標輪換操作,即i→j,j→m,m→i.因此,通過坐標轉換可獲得全局坐標系下應變矩陣

將式(16)～式(19)代入式(20)可得

其中,D和ttri分別代表3 節點三角形面單元的彈性剛度矩陣和單元厚度.

在使用FORTRAN 對ABAQUS 用戶子程序進行二次開發時,單元應變矩陣和單元剛度矩陣是參與計算迭代和數據更新中最為重要的兩個指標,可分別通過式(21)和式(22)計算得到.為準確構建納米表面單元,還必須建立表面參數與3 節點三角形面單元材料參數之間的關聯.

3 節點三角形面單元的物理方程可表示為

在平面應力問題中,彈性剛度矩陣可表示為

其中,Etri和vtri分別為單元的彈性模量和泊松比.

根據Gurtin-Murdoch 表面模型定義,納米表面物理方程可表示為

其中,σS和 εS為表面應力張量和表面應變張量,IS為表面單位張量.將式(23)與式(25)進行對比,不難得出以下關系

利用式(21)、式(22)和式(26)構造表面單元剛度矩陣,隨后連同表面殘余應力,代入單元平衡方程即可完成對Gurtin-Murdoch 型納米表面單元的構建.

1.4 有限元模型和材料參數

為納米多孔金屬選取合適的微觀結構是多尺度力學框架的關鍵一環,分別選取含1/8 球孔、單球孔和隨機多球孔的3 種模型進行研究,其中,1/8 球孔模型用來驗證所開發有限元程序的有效性,單球孔模型用來分析表面效應對材料吸能性的影響,以及模型參數對材料楊氏模量和壓縮屈服強度的影響,多球孔模型則包含一組具有相同孔徑并隨機分布的圓形孔洞,用來探究三維多孔金屬材料的單軸壓縮應力應變曲線、楊氏模量和壓縮屈服強度.需要注意的是,本文所定義壓縮屈服強度為壓縮應力應變曲線屈服平臺應力波動段中應力最低點對應的應力.圖3 展示了上述3 種有限元模型的示意圖.

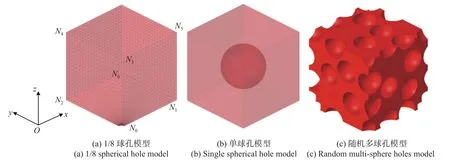
圖3 有限元模型Fig.3 Finite element model

為與參考文獻[13]無限大空間中孔洞附近應力場作對比,將1/8 球孔模型的孔洞半徑R0設為10 nm,邊長設為20 倍孔徑,以消除模型邊界影響.如圖3(a)所示,分別約束面N0N2N4N3沿x方向的位移、面N0N1N5N3沿y方向的位移和面N0N1N6N2沿z方向的位移.采用與參考文獻[13]相同的材料參數,即基體材料為線彈性鐵材,楊氏模量E和泊松比v分別取為177.33 GPa 和0.27,表面殘余應力τ0為1.70 N/m,表面拉梅常數λ0和μ0分別取為-8.00 N/m 和2.50 N/m.

對單球孔和隨機多球孔模型則采用周期性邊界條件,按下式分別對立方體代表性體元邊界面、棱和頂點處的節點位移進行約束[31]

2 結果與討論

2.1 有限元程序校驗

為驗證所開發有限元程序的有效性,選取1/8球孔模型進行有限元仿真,沿z軸施加100 MPa 的單軸拉伸應力,如圖4(a)所示.邊界條件和材料參數按1.4 節設置,表面和基體單元分別按1.3 小節設置,單元總數約5 萬個.

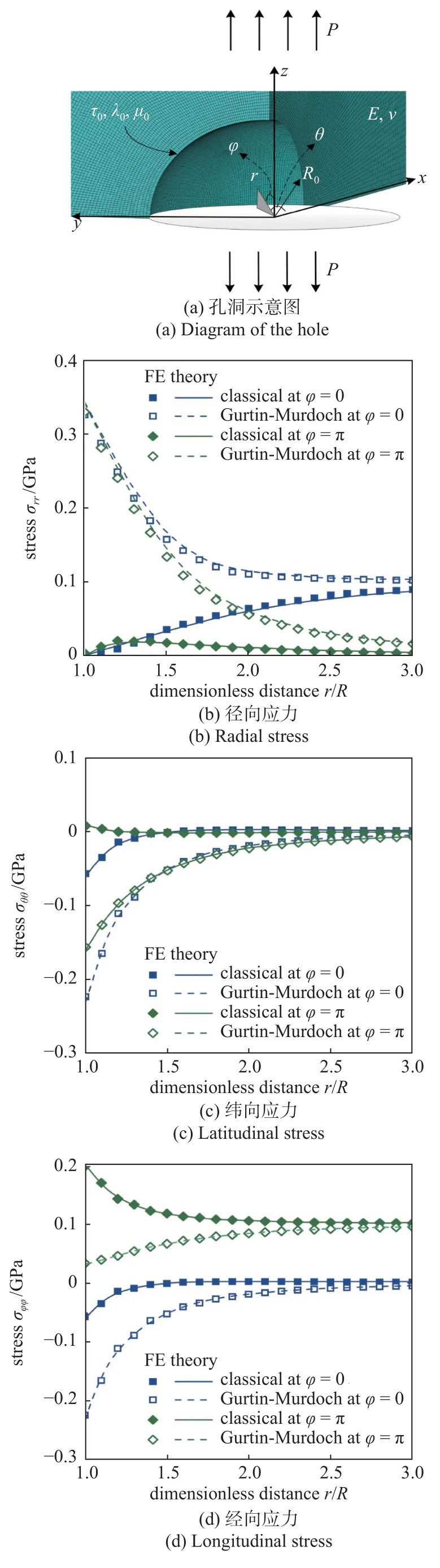
圖4 1/8 球孔模型附近應力分布Fig.4 Stress distribution near 1/8 spherical hole model

圖4(b)～圖4(d)所示為分別考慮經典和Gurtin-Murdoch 表面模型的球孔附近(φ=0 和 φ=π) 徑向、緯向和經向應力分布曲線,其中散點代表利用本文所開發計算模型得到的數值解,曲線代表He 等[13]所發展的解析解.通過比較可以發現,圖中散點能夠較為精準地落在對應的曲線上,這表明所開發的計算模型能夠有效地捕捉球孔附近應力響應.此外,考慮表面效應的模型在孔洞表面出現了不同程度的應力集中,隨著觀測位置遠離孔洞,考慮表面效應的應力分布曲線逐漸與經典工況重合,這說明表面效應對彈性體應力場的影響只在數倍于孔徑的范圍內較為明顯.

圖5 為球孔附近von Mises 應力云圖.在經典工況下,應力集中出現在xy平面與孔洞表面的交匯處,而xz平面、yz平面和孔洞表面的交匯處出現了應力凹陷.相對于經典工況,考慮表面效應的孔洞表面整體應力水平有所提升,但應力集中發生在xz平面、yz平面和孔洞表面的交匯處(經典工況的應力凹陷處).由此可見,表面效應不僅加劇納米多孔金屬表面應力集中,還改變應力集中出現的位置.

2.2 單球孔模型分析

納米多孔金屬材料是一種優良的吸能材料,在壓縮載荷作用下,經過較小的彈性變形階段之后,會進入一個較長的應力平臺階段,在這個階段,應力水平相差不大,但應變卻快速增加,因此材料能在較為穩定的應力水平下吸收大量的能量,此后隨應變進一步增加,應力迅速上升,材料進入密實化階段.為衡量納米多孔金屬材料的吸能性,分別采用應變能密度vε和能量吸收率pe作為吸能指標

其中,εm代表任意應變,σm為對應的應力.由定義可知,應變能密度即單位體積材料所儲存的應變能,反映納米多孔金屬的能量吸收能力,而能量吸收率為材料所吸收能量與對應應力之間的比值,當能量吸收率達到最大值時,表明在該應力水平下,材料的吸能效率最高.

首先對結構形式較為簡單的單球孔模型力學性能進行研究,選取模型為10 nm×10 nm×10 nm 的立方體,孔隙率 ρ 分別設置為10%,20%,30% 和40%.沿z軸負方向施加最大7 nm 的位移載荷,按1.4 節設置周期性邊界條件和對應的材料參數,表面和基體單元分別按1.3 小節設置,為保證計算精度,每個模型中單元數量不低于150 萬個.對孔洞表面進行自接觸設置,表面法向接觸為硬接觸,切向接觸的摩擦系數為0.1.

圖6(a)為單軸壓縮下不同模型和孔隙率的納米單球孔模型應變能密度隨應變的改變.可以發現,曲線分為線性和非線性兩區域,其中,當應變較低(小于0.4)時,由于對應的應力-應變曲線處于應力平臺階段,應力水平較為平穩,因此應變能密度隨應變呈線性增長.當應變較高(大于0.4)時,由于模型進一步被壓實,進入密實化階段,壓縮應力迅速增加,致使材料吸收更多的應變能,因此應變能密度隨應變呈非線性增長.

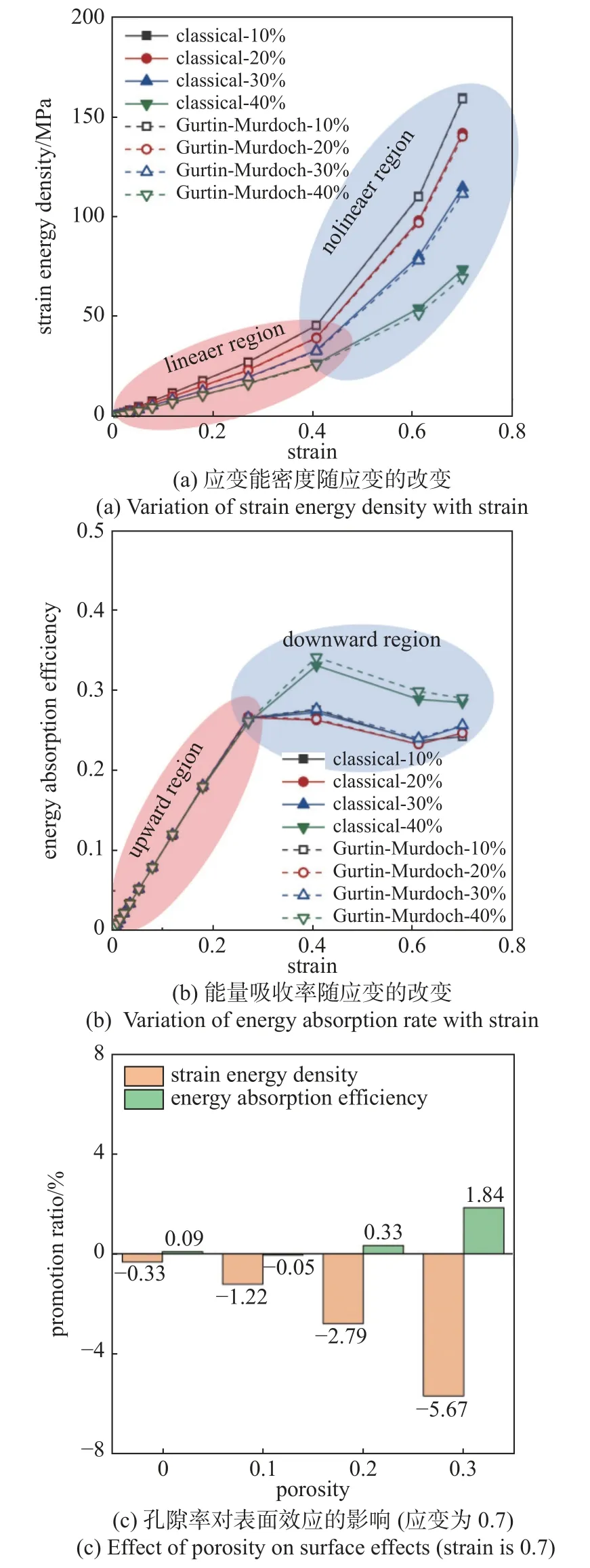
圖6 單軸壓縮下不同表面模型和孔隙率的納米單球孔模型應變能密度,能量吸收率隨應變的改變以及孔隙率對表面效應的影響Fig.6 Variation of strain energy density energy absorption rate with seain,and effect of porosity on surface effects for nano single sphere hole model with different surface models and porosities under uniaxial compression

圖6(b)為單軸壓縮下不同模型和孔隙率的納米單球孔模型能量吸收率隨應變的改變.能量吸收率曲線可分為上升和下降兩個區域,當應變量達到0.4 左右時,材料的能量吸收率達到最大,說明在應力平臺即將結束時,材料的吸能效率最高.在密實化階段,雖然材料吸能性得到進一步提升,但吸能效率卻呈現出下降趨勢,這同樣也是由于壓縮應力進一步增加導致的.

圖6(c)展示了不同孔隙率下表面效應對模型應變能密度和能量吸收率的提升比例.相對于經典工況,表面效應降低了模型應變能密度,但提高了模型能量吸收率,產生這一現象的原因是考慮表面效應模型的應力-應變曲線中應力水平低于經典工況[33],因此吸收的總能量也低于經典工況,也正是因為較高的應力水平,導致模型吸能效率的降低(見式(28)).此外,隨著孔隙率的增加,表面效應對應變能密度和能量吸收率的影響都逐漸增強,這是由于高孔隙率時模型比表面積較大,導致表面效應更加明顯.

圖7(a)為單軸壓縮下納米單球孔模型的楊氏模量和壓縮屈服強度隨孔隙率的變化.考慮表面效應的楊氏模量小于經典工況,而壓縮屈服強度卻與經典工況接近.在高孔隙率下表面效應對楊氏模量的降低效果更加明顯,例如,當孔隙率為10%時,考慮表面效應的楊氏模量相對于經典工況降低了0.7%,而當孔隙率為40%時則降低了2.9%,這一規律與圖6 中應變能密度隨孔隙率變化類似,同樣也是因為高孔隙率模型的比表面積更大導致的.

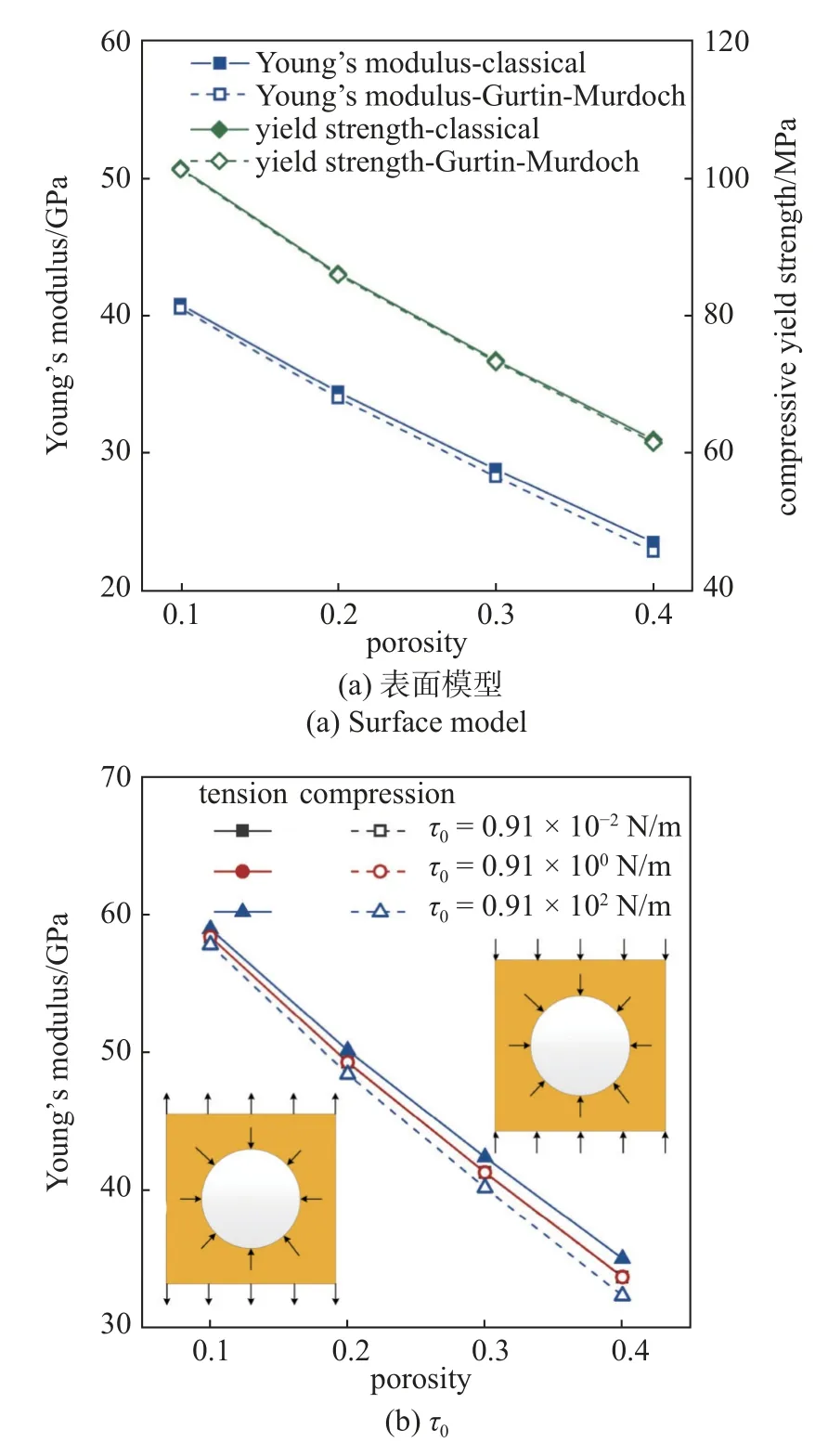
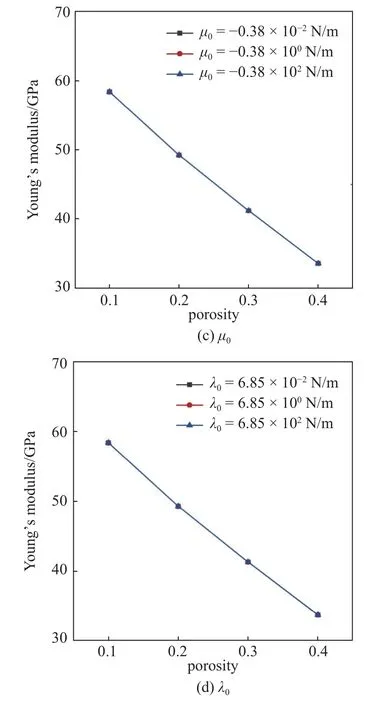
圖7 納米單孔模型楊氏模量或壓縮屈服強度隨孔隙率變化Fig.7 Variation of Young's modulus or compressive yield strength with porosity for nano single sphere hole model

如圖7 中圖例所示,為研究表面參數對納米單孔模型力學性能的影響規律,以2.2 節中納米鋁表面參數為基準,選取不同量級的數值進行研究.采用控制變量法,在研究表面殘余應力的影響時,令表面拉梅常數為零,在研究表面拉梅常數的影響時,令表面殘余應力保持0.91 N/m 不變.

由圖7(a)可知,表面效應對納米單孔模型壓縮屈服強度的影響較小,因此圖7(b)～圖7(d)僅展示采用不同表面殘余應力和表面拉梅常數條件下納米單孔模型楊氏模量隨孔隙率的改變.可以發現,表面拉梅常數對楊氏模量的影響較小,相比之下孔洞表面殘余應力對楊氏模量的影響較為顯著.此外,從圖7(b)可以發現,表面殘余應力對楊氏模量的影響強烈依賴于外載荷方向,當加載方向為拉伸時,表面殘余應力對材料楊氏模量有增強效果,而當加載方向為壓縮時,表面殘余應力則降低了材料楊氏模量.由于正向的表面殘余應力有促使孔洞收縮的效果[13,34],因此在壓縮載荷作用下,孔洞收縮促進了材料的壓縮變形,這導致材料楊氏模量的減小.在拉伸載荷作用下,孔洞收縮抵抗了材料拉伸變形,這導致材料楊氏模量的增加.值得注意的是,宏觀材料的楊氏模量屬于材料固有屬性,一旦確定結構形式和材料類型,其楊氏模量不受加載條件等外界因素影響,而通過以上分析可知,納米結構的楊氏模量不僅與表面參數相關,還與加載方向密切相關,不同的加載方向甚至可以改變表面效應對楊氏模量影響趨勢.

2.3 隨機多球孔模型分析

為考慮模型非均勻性的影響,選取具有相同孔徑的隨機多球孔模型進行研究,模型仍取10 nm×10 nm×10 nm 的立方體,孔隙率 ρ 分別為10%,20%和30%,孔洞數量分別為5,10,15 和20 個,如圖8(a)所示.沿z軸負方向施加最大值為6 nm 的單軸壓縮位移載荷,邊界條件、單元類型、單元數量和接觸設置與2.2 節相同.

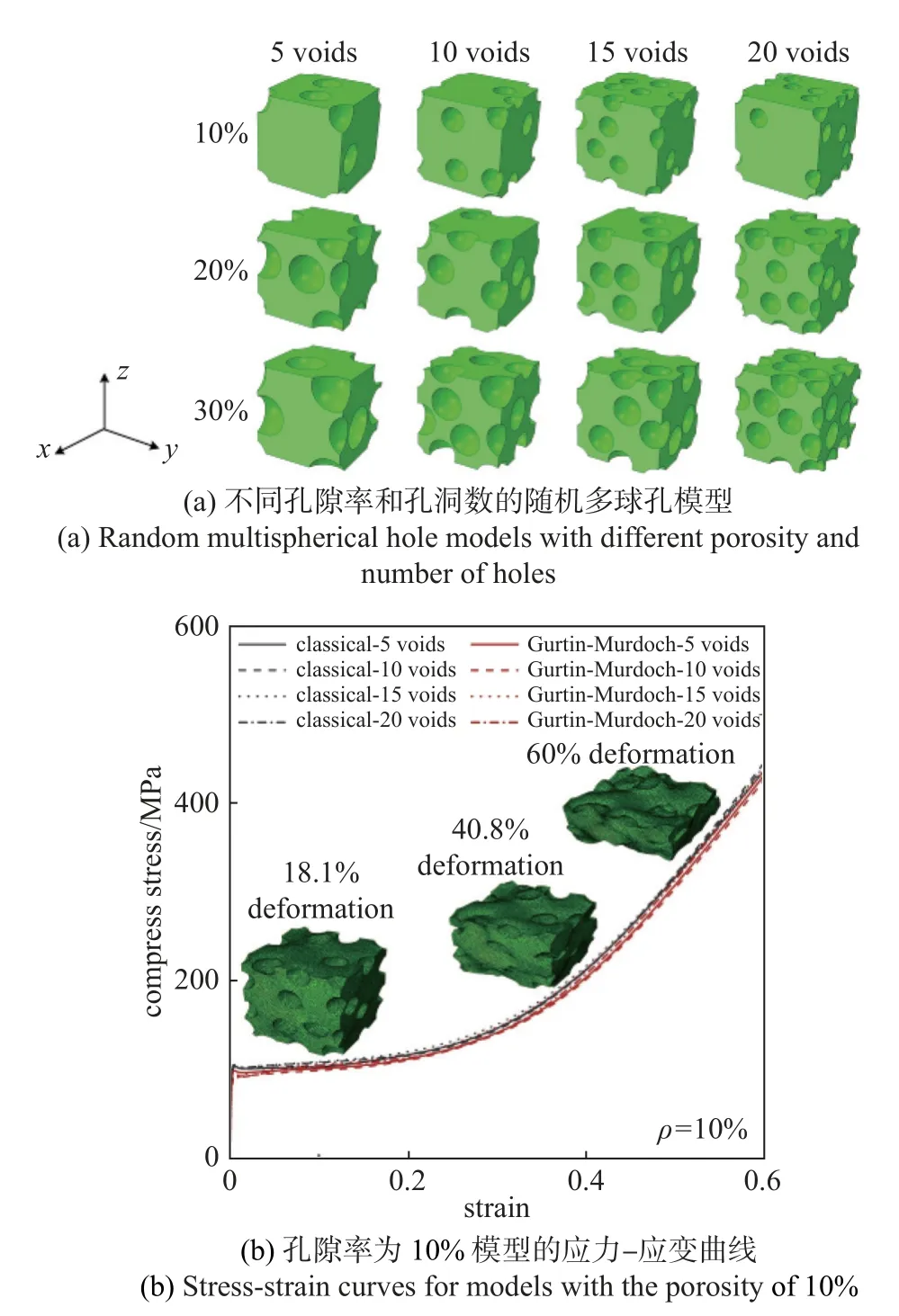
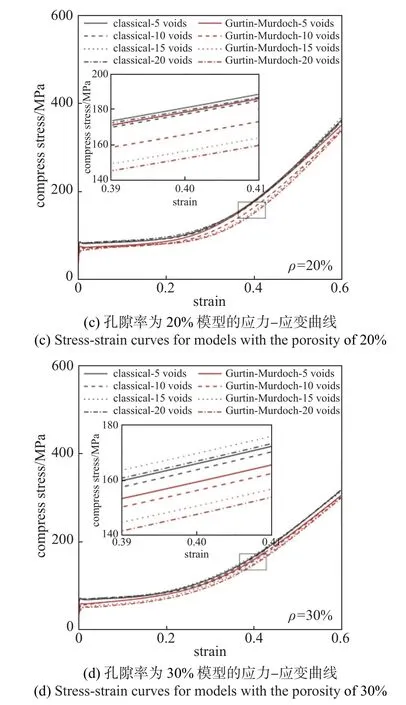
圖8 單軸壓縮下不同孔隙率和孔洞數的隨機多球孔模型及應力-應變曲線Fig.8 Under uniaxial compression,random multispherical hole models with different porosity and number of holes,and stress-strain curves for models

圖8(b)～圖8(d)展示了單軸壓縮下不同孔隙率的納米隨機多球孔模型單軸壓縮應力-應變曲線.可以發現,單軸壓縮應力-應變曲線出現了與傳統多孔材料類似的彈性、應力平臺和密實化3 個階段.當孔隙率為10%時,考慮表面效應的應力-應變曲線和經典工況幾乎重合.當孔隙率為20%和30%時,考慮表面效應的曲線應力水平明顯低于經典工況,并且從放大圖中可以觀察到其與孔洞數量成負相關,而在經典工況下卻無法觀察到類似的規律.這說明相同孔隙率下,納米多孔金屬材料具有尺寸效應,減小孔洞尺寸會增強材料的表面效應,而宏觀材料的應力-應變曲線是獨立于孔洞尺寸的.

圖9 為單軸壓縮下隨機多球孔模型楊氏模量和壓縮屈服強度隨孔隙率和孔洞數量的變化.可以觀察到,表面效應不同程度上降低了材料的楊氏模量和壓縮屈服強度,這與圖8 中表面效應對曲線應力水平的影響規律類似.此外,在相同的孔隙率下,經典工況的模型楊氏模量和壓縮屈服強度并不隨孔洞數量改變,而考慮表面效應的模型楊氏模量和壓縮屈服強度隨孔洞數量的增加逐漸下降,這一現象與圖7(a)保持一致,需要指出的是,圖7(a)中表面效應對模型楊氏模量的影響并不像圖9 那樣明顯,這是由于相同孔隙率下多孔模型具有更高的比表面積,因此表面效應更為顯著.

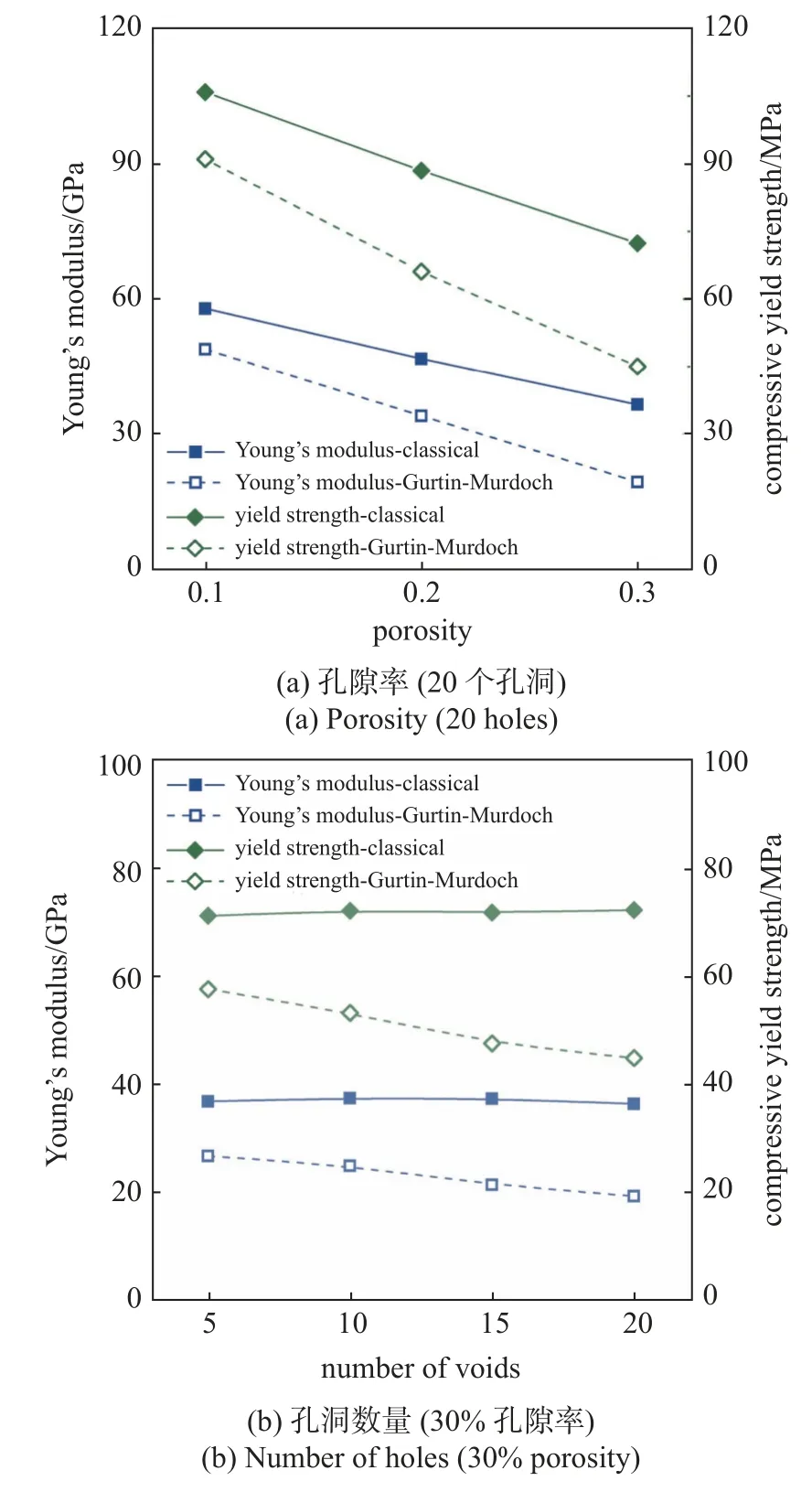
圖9 單軸壓縮下隨機多球孔模型的楊氏模量和壓縮屈服強度隨孔隙率和孔洞數量的變化Fig.9 Young's modulus and compressive yield strength of the random multi-sphere holes model in uniaxial compression vary with porosity and number of holes

由于缺乏可對比的實驗數據,本文僅采用1/8球孔模型、單球孔模型和隨機多球孔模型來對納米多孔金屬材料力學性能進行研究,所開發的有限元模型基于納米表面理論和有限元原理,因此該方法并不受微觀建模限制,仍可適用于一般納米多孔金屬結構.可以預見,對于具有復雜微觀結構的納米多孔金屬材料,可借助專業建模程序(如SOLIDWORKS)和網格劃分程序(如HYPERMESH)進行建模和離散,在此基礎上結合本文所構建的有限元表面單元即可完成對復雜納米結構力學性能的預測.

3 結論

本文基于能量最小原理,將Gurtin-Murdoch 表面模型引入有限元方程,通過為納米表面構建有限元單元的方式,發展了可捕捉三維納米多孔金屬材料表面效應的有限元計算模型,在此基礎上揭示孔隙率、孔洞數量和表面參數等因素對楊氏模量、壓縮屈服強度和吸能性等力學性能的影響規律,得到以下主要結論.

(1) 通過與參考文獻應力分布對比分析,驗證了所開發有限元計算模型的準確性.表面效應不僅加劇納米多孔金屬表面應力集中,還改變應力集中出現的位置.

(2) 盡管考慮表面效應的納米多孔金屬材料應變能密度低于經典工況,但能量吸收率卻高于經典工況.表面拉梅常數對楊氏模量的影響較小,而孔洞表面殘余應力對楊氏模量的影響較為顯著.與宏觀結構不同,納米結構楊氏模量不僅依賴于表面參數,還與加載方向密切相關.

(3) 相同孔隙率下,納米多孔金屬材料具有尺寸效應,減小孔洞尺寸會增強材料的表面效應,而宏觀材料的應力-應變曲線是獨立于孔洞尺寸的.