空間機械臂面向太陽能帆板在軌清潔任務的擦抹力/位阻抗控制1)
朱 安 陳 力
* (江西理工大學能源與機械工程學院,南昌 330013)
? (福州大學機械工程及自動化學院,福州 350108)
引言
為了持續、深入地探索太空,人類向太空發射了大量攜帶有各類電子設備的探測衛星.太陽能帆板是衛星系統的電能收集裝置,若其供電不足以支持系統內電子設備的正常運行,衛星的大部分功能將被限制,這是影響衛星壽命的重要因素之一[1-3].衛星一般通過燃燒攜帶的燃料對位姿進行調節,但燃燒形成的煙霧容易附著在太陽能帆板上;另外,超高速碎片撞擊產生的分子態污染物也容易附著在太陽能帆板上,這些污染物將極大地降低帆板的工作效率,嚴重時甚至會導致衛星失效[4-6].參考文獻[6]的數據,美國在1996 年的統計中發現衛星因受污染發生失效的有25 顆.因此,對衛星的太陽能帆板進行定期清潔具有重要的研究意義.
目前對地面太陽能電池板的清潔方式主要有:雨水和風自然清潔、空氣調節系統清潔、噴水設備清潔、人工清潔、機器人清潔等[7-9].但衛星工作在微重力、高真空和大溫差的太空環境中,采用空間機械臂對其太陽能帆板進行清潔是一種合適且有效的方法.值得注意的是,與地面太陽能電池板的安裝方式不同,衛星的太陽能帆板一般以懸臂的形式安裝[10],在清潔時為了保護太陽能帆板不被破壞,需對衛星姿態、清潔裝置位姿與輸出力進行非常精細的控制.另外,由于太陽能帆板存在一定的柔性,清潔操作中引起的帆板柔性振動將很難被抑制,故對空間機械臂清潔操作的研究有一定的難度.
針對機械臂與外界環境的接觸、碰撞問題,Hogan[11]提出的阻抗控制可通過調整阻抗參數,構建機械臂末端位姿與輸出力之間的動態關系,實現接觸與碰撞的柔順化.在Hogan 研究的基礎上,曾晨東等[12]針對空間機械臂在軌插拔孔操作的控制問題,設計了一種事件觸發滑模阻抗控制策略.Kang 等[13]為提高空間機械臂捕獲航天器的效率和安全性,提出一種基于阻抗控制的PD 組合控制策略.Liu 等[14]為保持機器人與非合作衛星之間的接觸以降低衛星的旋轉速度,提出了一種避免中心碰撞后分離的阻抗控制方案.考慮到空間機械臂對太陽能帆板進行清潔操作時,需同時實現衛星位姿、清潔裝置位姿與輸出力的精確控制,因此本文結合阻抗控制原理,并參考文獻[15]的力/位伺服系統,設計了一種力加載隨動控制系統.其可根據清潔裝置輸出力與接觸力的誤差,在線修正清潔裝置的位姿與輸出力.
針對空間系統的控制問題,宋新宇等[16]研究了撓性航天器動力學模型的非約束模態.郭聞昊等[17]基于粒子群算法對空間機器人抓捕衛星碰撞前構型進行優化,減小了碰撞對機器人系統角動量的影響.范紀華等[18]針對多桿空間鏈式柔性機器人系統,采用假設模態法、有限元法、Bezier 插值法和B 樣條插值法對變形場進行描述.機械臂在清潔操作的各階段切換時會因系統狀態變化導致清潔裝置輸出力突變,過大的輸出力將造成太陽能帆板的損壞.近年來,障礙Lyapunov 函數(barrier Lyapunov functions,BLFs)在求解時變約束問題上取得了較好的效果[19-22],為了盡量減小輸出力突變造成的影響,本文針對機械臂清潔太陽能帆板的控制特點,設計了一種對數型的BLFs 約束系統狀態,且基于此提出了一種全狀態約束控制(full state constraint control,FSCC)策略.該策略將BLFs 運用在控制器的每一步反演設計中,有效地防止了設置的約束被突破.
一般情況下,由于攜帶的燃料消耗、機械臂質心偏移等原因,衛星系統的參數難以精確獲得,而RBF 神經網絡(RBF neural networks,RBFNN) 對非線性不確定系統具有很好的擬合效果[23-26],考慮到學者對RBFNN 的研究已相對成熟,因此本文采用Huang 等[27]提出的RBFNN 對衛星系統的不確定參數進行擬合.另外,考慮到太陽能帆板的柔性及衛星與機械臂系統存在的動力學耦合問題,在清潔操作中微小的振動將可能引起帆板的激振,嚴重時可能導致設備的損壞.即使未產生激振,由于清潔操作對位姿與輸出力均有較高的要求,從此方面考慮也有必要對帆板的柔性振動進行抑制.為此本文參考文獻[28],運用虛擬力的概念,采用混合軌跡法對帆板的柔性振動進行抑制.
本文對機械臂擦抹清潔衛星太陽能帆板操作進行了研究,導出了衛星姿態受控形式的系統動力學模型.結合阻抗控制原理,設計一種力加載隨動控制系統在線修正清潔裝置的位姿與輸出力.提出一種基于BLFs 的FSCC 策略,且通過RBFNN 擬合系統不確定參數提高了控制的精度.
1 動力學建模
機械臂清潔衛星太陽能帆板操作如圖1 所示.圖1 中O0,Oci和Oi(i=1,2,3) 分別為衛星載體質心、機械臂質心和各關節鉸中心,Os為帆板的起始點,P為清潔裝置的末端點;XOY為系統隨軌道平動的慣性參考坐標系;x0O0y0為固定在衛星載體質心上的坐標系,xiOiyi為固定在關節鉸中心的坐標系.文中所用部分符號定義如表1 所示.

表1 部分符號定義Table 1 Definition of some Symbols
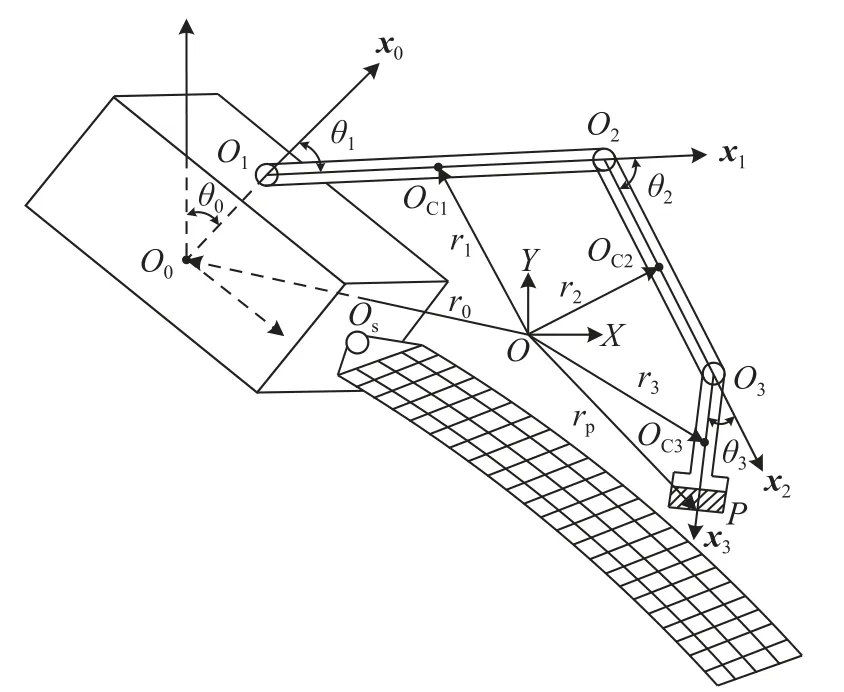
圖1 衛星太陽能帆板清潔機械臂Fig.1 Satellite solar panel cleaning manipulator
清潔操作中衛星太陽能帆板的彎曲如圖2 所示,通過參考文獻[29]可將太陽能帆板等效為簡支梁.為方便后續建模分析,選取太陽能帆板軸線方向與直線O0Os重合,取其抗彎剛度EI與線密度 ρs均為定值.
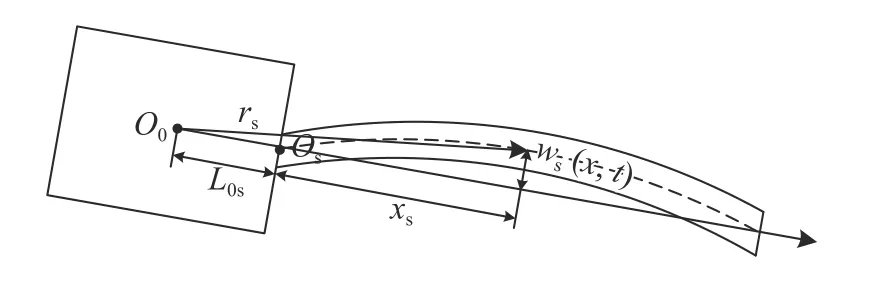
圖2 太陽能帆板的彎曲Fig.2 Bending of solar panel
圖2 中xs(0 ≤xs≤Ls) 為太陽能帆板與Os的軸向距離,為t時刻太陽能帆板在xs處的徑向柔性位移,?g(xs),δg(t) 分別表示帆板的第g階模態函數與模態坐標,這里取n=2.
通過圖1 和圖2 可知,在慣性參考坐標系XOY下各分體質心的位置矢徑為
由于在清潔操作中系統未受外力影響,且衛星的位置不受控,因此整個系統滿足動量守恒關系.若令系統的初始動量為零,則通過系統動量守恒關系可得
式中,Nυ,k,Nυ,s,Ns,k和Ns,s均為包含系統參數的常量.
通過式(2)可得系統的動能為
式中,ωk為系統第k個分體的角速度.
若忽略太空的微重力影響,則系統的勢能來源于太陽能帆板,因此系統勢能為
將T與U的表達式代入如下形式的Lagrange方程
式中,L=T-U為Lagrange 函數,Q∈R6×1為系統的廣義力,q=[θ0,θ1,θ2,θ3,δ1,δ2]T為系統的廣義坐標.
通過式(5)可得系統動力學模型為
式中,Mr11∈R4×4,Mr12∈R4×2,Mr21∈R2×4,Mr22∈R2×2為系統的慣量矩陣Mr的分塊矩陣,Hr11∈R4×4,Hr12∈R4×2,Hr21∈R2×4,Hr22∈R2×2為包含科氏力、離心力矩陣Hr的分塊矩陣;qr=[θ0,θ1,θ2,θ3]T,δ=[δ1,δ2]T,Kδ∈R2×2為帆板的等效剛度矩陣,τr=[τ0,τ1,τ2,τ3]T為載體姿態、關節的控制力矩.
通過式(6)對系統進行剛柔性分解,得系統的剛性動力學模型為
由于清潔操作考慮的是清潔裝置相對衛星載體的運動情況,故將P點在x0O0y0上投影可得
式中,xO1和yO1為O1在x0O0y0下的位置坐標,θP=θ1+θ2+θ3.
通過式(8)可得P點相對載體的運動學關系為
通過式(9)可將式(7)所示的關節空間動力學模型轉換為基于末端位置的慣性空間動力學模型
2 阻抗模型
阻抗控制可通過設置合適的阻抗參數調節機械臂位姿和接觸力之間的關系,考慮到擦抹清潔操作中為了防止發生劇烈的接觸、碰撞,需精確控制機械臂末端輸出力與位姿,故將阻抗控制應用于擦抹清潔操作.
參考文獻[30],機械臂的阻抗關系可描述為
式中,Xd為期望位姿,X為實際位姿;MP∈R4×4,BP∈R4×4,KP∈R4×4分別為慣量矩陣、阻尼矩陣、剛度矩陣;Fd∈R4×1,Fe∈R4×1分別為清潔裝置的期望輸出力與實際接觸力.
根據是否需要控制清潔裝置的輸出力,清潔操作過程可分為自由和接觸兩個階段.在自由階段,清潔裝置末端的接觸力為零;在接觸階段,清潔裝置末端受到環境力的作用,其運動狀態受到限制.因此擦抹清潔操作中阻抗關系可描述為
3 控制器設計
3.1 預備知識
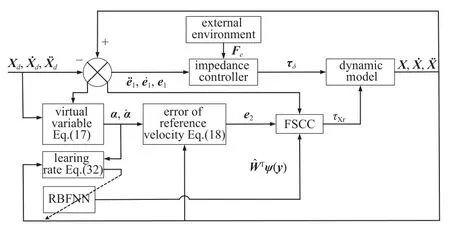
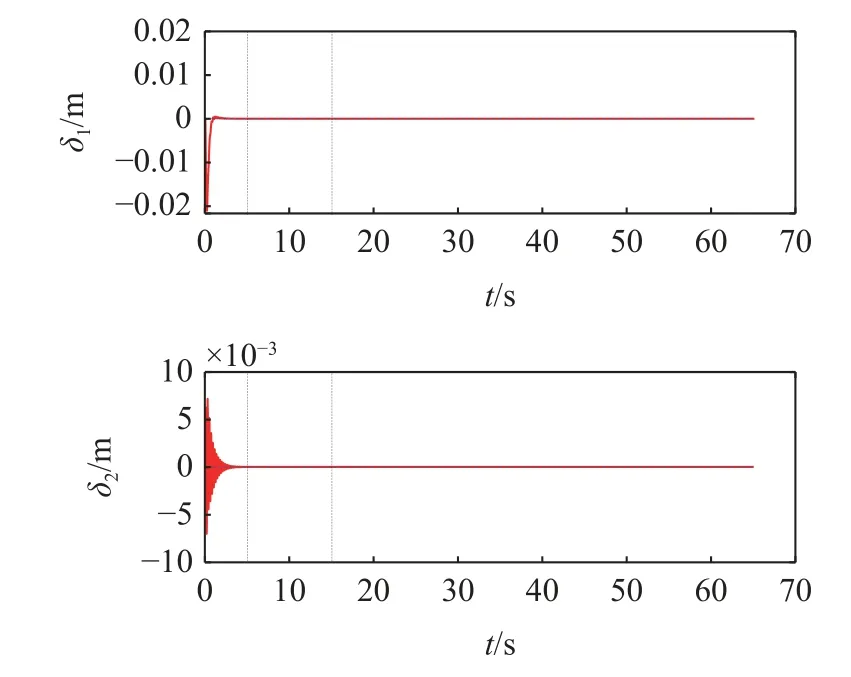
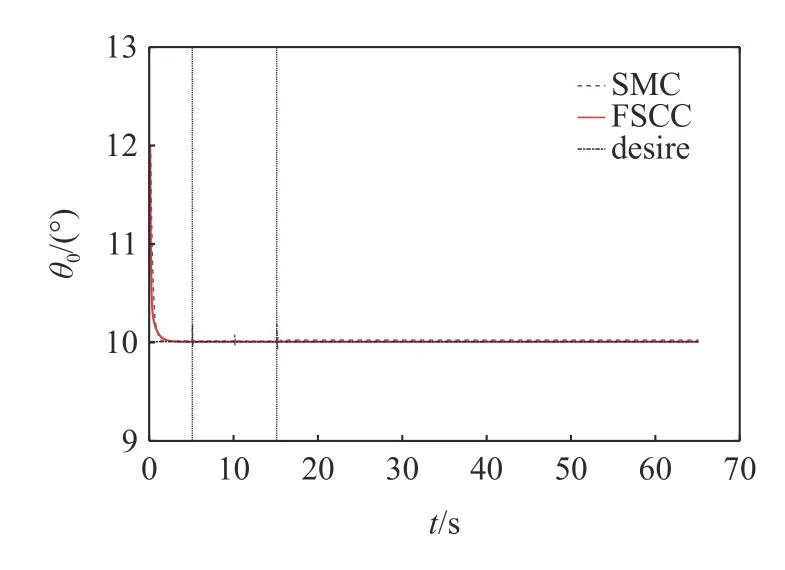
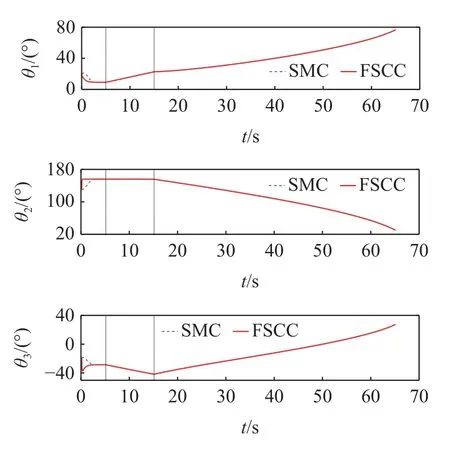
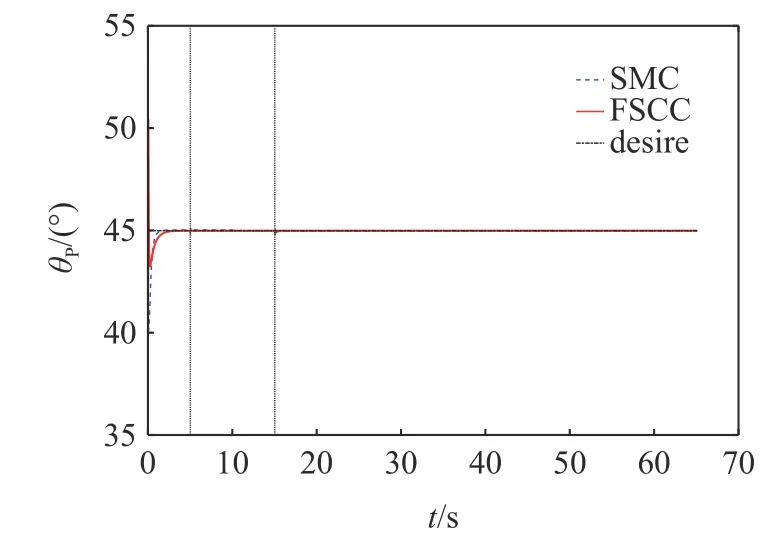
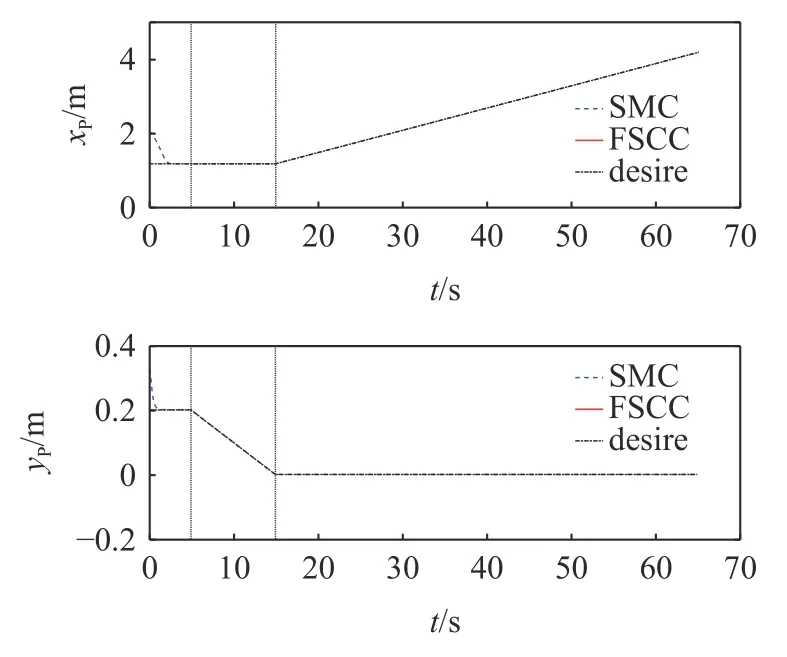
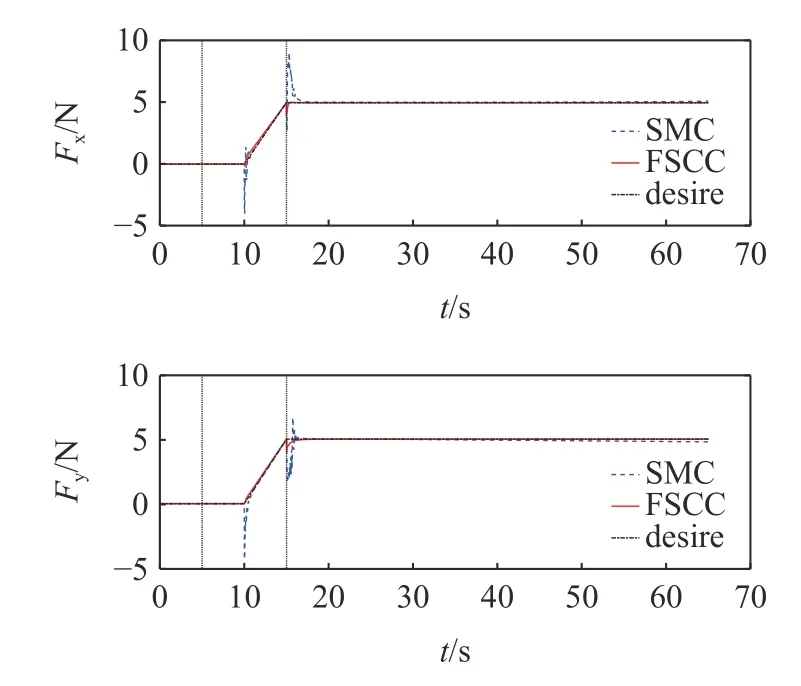
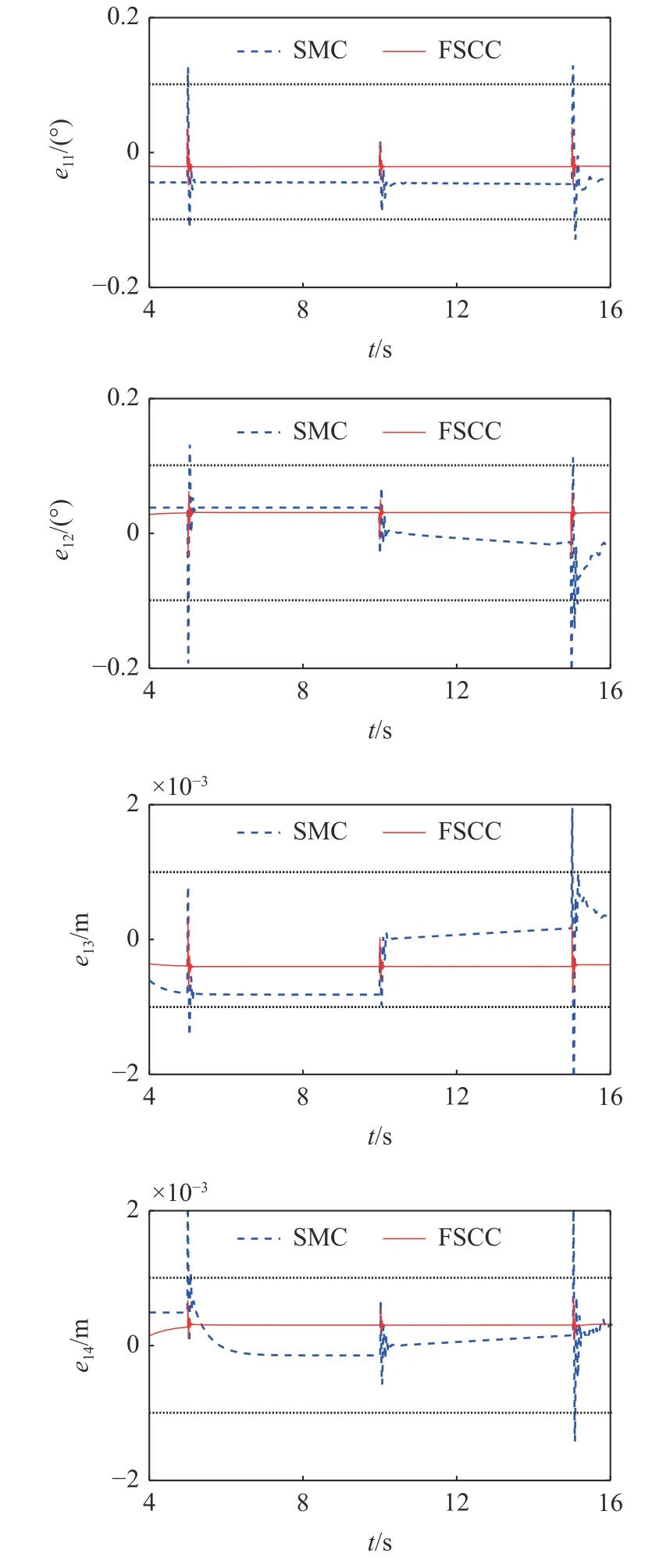
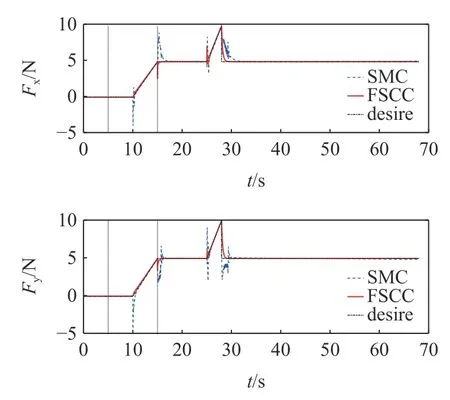
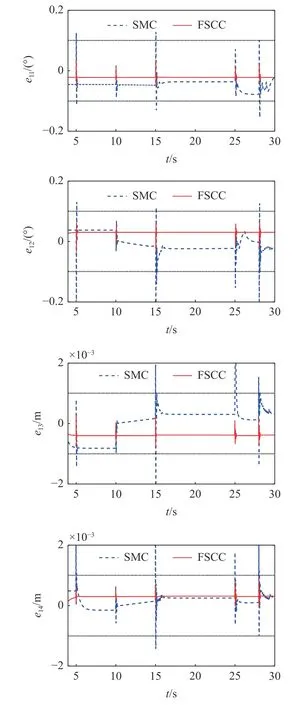
定理1對于大于零的常數ka與任意的變量x,若滿足條件 |x| 這里稱ka為x的約束值. 在定義域y∈(0,+∞) 內,有不等式y-1 ≥lny成立,則可知定理1 成立. 式中,Γj>0 為增益系數,ψj(y) 為神經網絡的基函數,且 ‖ψ(y)‖≤ψN;y為神經網絡的輸入,εj>0 為很小的正數,用于提高控制器的魯棒性. 假設1神經網絡對不確定項的逼近誤差 ? 有界,即 ‖?‖≤?N,?N>0. 將式(10)的動力學模型改為狀態空間表達式 定義如下形式的位置與速度誤差 式中,zd=Xd為清潔裝置的期望位姿. 設計如下形式的虛擬變量 基于式(17)設計如下參考速度誤差 通過式(16)~式(18)可得 對式(18)求導且結合式(15)可得 為防止機械臂在運動過程中突破設置的狀態約束,采用反演算法設計控制力矩.首先選取如下形式的Lyapunov 函數 對式(21)求導且結合式(17)和式(19)可得 式中,e2j為e2中的元素. 基于式(21)和式(22)選取新的Lyapunov 函數 對式(23)求導可得 結合特性1 與式(20),式(24)可化簡為 根據Moore-Penrose 偽逆矩陣有 式(27)設計的控制率需精確知道系統的參數,然而其一般難以精確獲得,由此導致 ρ(t) 的不確定.ρ(t)的不確定將嚴重降低系統的位姿與輸出力控制精度,考慮到RBFNN 可較好地對非線性項進行擬合,故采用RBFNN 對 ρ(t) 進行擬合. 假設存在理想的權值矩陣W*使得 ρ (t) 可以被擬合為 式中,νn和 ?n分別為高斯基函數的中心和寬度. 由于W*為理想值,其存在但不可知,因此在控制中對不確定項 ρ(t) 擬合的實際值為 通過式(30),控制率式(27)被改寫為 參考文獻[27]設計如下形式的RBFNN 學習率 定理2對于式(10)所示的系統,若滿足假設1,且采用式(31) 所示的控制力矩,式(32) 所示的RBFNN 學習率,則可保證系統全狀態收斂. 證明選取如下的Lyapunov 函數 對式(33)求導可得 將式(31)和式(32)代入式(34)可得 結合定理1、引理1 與式(36),式(35)可被化簡為 基于以上分析,只要滿足 λminK2-3E/4>0 即可保證系統收斂.進一步,對式(37)積分可得 式中,D1=V3(0)-C2/C1. 結合式(33)可知系統各狀態量的收斂域為 上節設計的控制器僅考慮了系統的剛性,未將帆板的柔性考慮在內.由于清潔操作對系統的控制精度有較高的要求,而太陽能帆板的柔性振動會對清潔操作的控制產生干擾,故本節采用虛擬控制力原理對設計的期望軌跡進行修正,使得太陽能帆板的柔性振動能被抑制. 引入虛擬力Fh∈R4×1,期望軌跡與混合軌跡誤差eh=zh-zd由如下二階指令發生器生成 式中,μ和η∈R4×4為正定常數矩陣. 將式(40)代入式(15)可得 結合式(39)和式(41)可得 將式(42)代入式(6)可得系統的柔性部分為 參考文獻[28] 可知,當取Fh=時可保證S收斂,即控制器可同時保證軌跡的高精度控制與帆板的振動抑制. 為了同時控制清潔裝置的位姿與輸出力,參考文獻[15]的力/位伺服系統,設計了一種力加載隨動控制系統,其控制框圖如圖3 所示. 圖3 力加載隨動系統控制框圖Fig.3 Control diagram of force load servo system 圖3 所示的控制系統可根據機械臂清潔裝置輸出力與接觸力的誤差,在線修正清潔裝置的位姿,并實現對輸出力的跟蹤. 采用圖1 所示的系統進行仿真分析,系統參數如下:m0=200 kg,m1=m2=10 kg,m3=5 kg,L0=0.5 m,L1=L2=2 m,L3=0.5 m,Ls=3 m,d1=d2=1 m,d3=0.25 m,Los=1.2 m,I0=128 kg·m2,I1=I2=15 kg·m2,I3=2 kg·m2,ρs=45 kg/m,EI=1000 N·m2. 控制參數如下:k1j=20,k2j=50,ka1=ka2=π/1800,ka3=ka4=10-3,Γj=40,εj=0.5,Mp=diag(100,100,100,100),Bp=diag(200,200,200,200),Kp=diag(500,500,500,500),μ=η=diag(5,5,5,5). 為保證清潔過程中對清潔裝置位姿與輸出力的精確控制,將整個過程劃分為3 個階段:預備階段、靠近階段和擦抹清潔階段.假設清潔裝置與帆板的摩擦系數為0.2,為防止自鎖,在清潔過程中清潔裝置與太陽能帆板的夾角應始終大于11.31o,系統的初始狀態為qr=[12o,20o,130o,-20o]T. (1) 預備階段:關閉阻抗控制,調整衛星的姿態與清潔裝置的位姿,使清潔裝置移動到太陽能帆板起始點Os的正上方,且調整清潔裝置與太陽能帆板的夾角.此過程中,衛星與清潔裝置的期望位姿、期望輸出力為 (2) 靠近階段:在5~10 s 調整清潔裝置位置,使其緩慢地靠近太陽能帆板;為防止清潔裝置與太陽能帆板在剛接觸時因輸出力太小而達不到預期的清潔效果,在10~15 s 開啟阻抗控制進行輸出力的預加載,且將清潔裝置移動到與太陽能帆板剛接觸.假設摩擦力為1 N,則衛星與清潔裝置的期望位姿、期望輸出力為 (3) 擦抹清潔階段:開啟阻抗控制,使清潔裝置沿期望軌跡克服太陽能帆板的摩擦阻力進行清潔操作,衛星與清潔裝置的期望位姿、期望輸出力為 首先分析清潔操作中太陽能帆板的柔性振動,及所采用的混合軌跡抑振方法對振動的抑制效果.仿真結果如圖4 和圖5 所示,其中圖4 為未采用抑振算法的帆板模態變化情況,圖5 為采用了抑振算法的能帆板模態變化情況. 圖4 未采用抑振算法的太陽能帆板模態Fig.4 Modal of solar panels without vibration suppression 圖5 采用抑振算法的太陽能帆板模態Fig.5 Modal of solar panels with vibration suppression 從圖4 可知,在未對帆板的柔性振動進行抑制的情況下,由于存在系統動力學耦合,帆板的振動幅度會越來越大,導致清潔操作無法完成.通過圖5 可知,所采用的抑振算法可有效抑制帆板的柔性振動,保證了清潔操作中對清潔裝置軌跡和輸出力的高精度控制. 接下來將在帆板柔性振動抑制的前提下,對所提控制策略的性能進行分析,且將其與文獻[33]中的滑模控制(sliding mode control,SMC)策略進行對比分析,SMC 中同樣采用RBFNN 擬合系統的不確定項,仿真結果如圖6~圖11 所示. 圖6 衛星載體姿態角軌跡Fig.6 Trajectory of satellite base attitude angle 圖6 為衛星載體的姿態角,圖7 為機械臂關節角,圖8 和圖9 為清潔裝置的位姿,圖10 為清潔裝置的輸出力,圖11 為載體與清潔裝置的位姿誤差(e11和e12為載體與清潔裝置姿態角誤差,e13和e14為清潔裝置x和y方向的位置誤差).由圖6 可知在清潔操作過程中,載體姿態角雖然在各階段的切換過程中產生了波動,但隨后迅速平穩.由圖7~圖9可知,清潔裝置的位姿可較好地跟蹤上期望值,且具有較快的響應速度.結合圖10 和圖11 可知FSCC策略下,BLFs 可在清潔操作的各階段切換中有效地避免系統狀態發生突變,從而防止清潔裝置輸出力發生突變,這是保證清潔操作安全執行的重要條件. 圖7 機械臂關節角軌跡Fig.7 Trajectory of the manipulator joint angles 圖8 清潔裝置姿態角軌跡Fig.8 Trajectory of the cleaning device attitude angle 圖9 清潔裝置位置軌跡Fig.9 Trajectory of the cleaning device position 圖10 清潔裝置輸出力Fig.10 Output force of the cleaning device 圖11 衛星與清潔裝置位姿誤差Fig.11 Position and attitude angle error of the satellite base and cleaning device 在擦抹清潔過程中可能會出現太陽能帆板結構變化導致局部摩擦力突變的情況,為保證在此情況下仍能順利地完成清潔任務,采取在摩擦力突變時保持載體與清潔裝置姿態不變,將清潔裝置輸出力緩慢增加至最大靜摩擦,待清潔裝置與帆板相對滑動后再將輸出力恢復至原值.假設在25 s 時候摩擦力突變至2 N,因此保持4.1 中的預備、靠近階段不變,將擦抹清潔階段調整為 仿真結果如圖12~圖14 所示,其中圖12 為清潔裝置的位置,圖13 為清潔裝置的輸出力,圖14 為衛星與清潔裝置位姿誤差. 圖12 清潔裝置位置軌跡Fig.12 Trajectory of the cleaning device position 圖13 清潔裝置輸出力Fig.13 Output force of the cleaning device 圖14 衛星與清潔裝置位姿誤差Fig.14 Position and attitude angle error of the satellite base and cleaning device 結合圖12 和圖13 可知,在25 s 摩擦力突變時清潔裝置保持末端位置不變,其輸出力緩慢增加,到28 s 時克服靜摩擦繼續執行清潔操作;且通過圖13 可知在各階段的切換中FSCC 的清潔裝置輸出力相較于SMC 更加平穩.通過圖14 可知,在清潔操作的各階段切換中,BLFs 可有效地將系統狀態限制在約束范圍內,保證了任務的安全、順利執行. 文章針對空間太陽能帆板的擦抹清潔操作進行了研究,得到以下結論. (1) 通過結合阻抗控制原理,擦抹清潔操作可較好地控制清潔裝置輸出力,使其在系統狀態發生突變時也能穩定輸出,在保證清潔效果的同時避免了對太陽能帆板的破壞. (2) 所采用的抑振算法可有效地抑制帆板的柔性振動,所提的FSCC 策略可將系統的狀態限制在設置的約束范圍內,且通過結合RBFNN 對不確定系統進行擬合,實現對衛星載體與清潔裝置位姿的精確控制. (3) 對太陽能帆板擦抹清潔操作進行分段控制可有效劃分操作的流程,在一定程度上保證清潔操作順利的完成.3.2 FSCC 控制器設計
3.3 太陽能帆板振動抑制
3.4 結合阻抗模型的FSCC
4 仿真模擬
4.1 摩擦力未突變下的擦抹清潔操作
4.2 摩擦力突變下的擦抹清潔操作
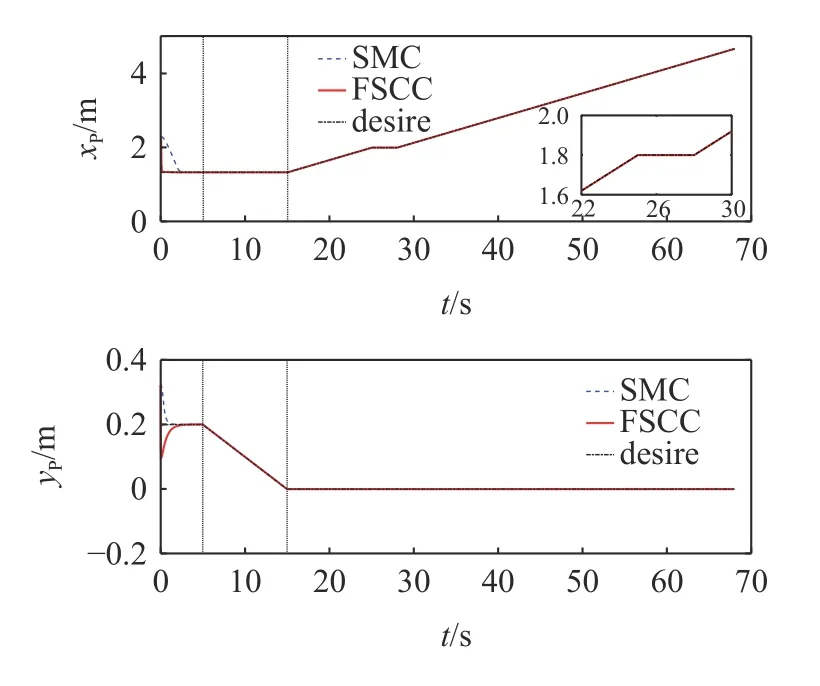
5 結論

