基于離散事件動態系統的染缸資源配置優化方法研究

余 婷，何經旺，林 勵，王子玥玥

（福建信息職業技術學院，福建 福州 350003）

目前，國內的印染企業仍對生產訂單進行人工染缸資源配置，企業自動化程度與生產效率較低。因此，對訂單進行合理的染缸資源配置，提高染機資源利用率，對印染企業具有重要意義。李可彪等[1]根據企業生產計劃流程建立了以投入生產染缸空閑量最少為目標、以有限生產資源為約束的染缸生產排缸模型。莫豐勇[2]則針對企業浸染生產過程中的加工設備多和調度復雜等特性，建立了一種用于浸染生產調度的數學模型，并用遺傳算法求解染缸配置。本研究基于福建晉江某紡織企業的染缸資源配置過程，用離散事件動態系統的方法對訂單排缸過程建立模型，再用動態規劃法尋找染缸最優配置策略，使訂單能在較短時間內順利加工完成并提高利用率。

1 染缸資源配置的離散事件動態系統模型

1.1 離散事件動態系統

離散事件動態系統（Discrete Event Dynamic System，DEDS）興起于20世紀80年代，由一些有復雜交互作用的事件驅動，系統狀態僅在一些離散時刻點隨著事件的發生而變化。形式語言/自動機是DEDS的基本建模工具[3]。一個確定的有限狀態自動機G為一個五元組[4]：G=(Q,∑,δ,q0,Qm)。其中，Q為有限狀態集合；∑為事件集（分可控事件集∑c和不可控事件集∑uc，且∑uc=∑/ ∑c）；δ為狀態轉移函數，即δ:Q× ∑→Q，描述系統由一個狀態經給定條件轉移至新狀態的過程；q0∈Q為初始狀態；Qm∈Q為標識狀態。若定義δ(q0,ε)=q0，且δ(q0,sσ)=δ[δ(q0,s),σ]，?σ∈∑，s∈∑*，則狀態轉移函數也可以擴展定義至符號串集合∑*，即δ:Q× ∑→Q。對于任一初始狀態q0∈Q，自動機G的生成語言為L(G)定義為使狀態轉移函數δ(w,q0)有定義的輸入符號串w∈∑*的一個集，用式子表示為L(G)={s∈∑*|δ(q0,s)!}。設有一個映射f:L(G)→Γ，表示當自動機G產生事件串s時的控制輸入為f(s)，下一個發生的事件需發生在f(s)∩{σ:δ(sσ,q0)!}中，則稱f為監控器，記f控制下的系統為f/G。在此，假設字符串s的長度為|s|，Lk(G)={s∈L(G)||s|=k}表示由自動機G生成的長度為k的字符串集合。當字符串長度|s|=k時，串s發生后，在監控器fk的作用下，所有可能的控制輸入fk(s)可表示為fk:Lk(G)→Γ，其中，s∈Lk(G)，Γ為控制輸入集。故控制器f為一系列決策序列f=(f0,f1,f2,…)。

1.2 染缸資源配置的離散事件動態系統建模

資源配置系統是一類典型的離散事件動態系統。針對染缸資源配置系統，規定配置規則：任一訂單均可通過某些染缸進行有限次的滿負荷加工及一次不滿負荷加工完成；若訂單質量小于染缸容量，則將訂單直接分配在合適的染缸進行生產；若訂單質量大于染缸容量，則需對訂單進行適當拆分，將其分配到若干染缸中生產。

本研究考慮對l種缸容的染缸資源配置系統建立自動機模型，使訂單的各種生產方式通過自動機狀態轉換圖表示出來，模型G:(Q,∑,δ,q0,Qm)。其中，Q={l種染缸工作狀態的集合}，0表示染缸處于空閑狀態，1表示染缸處于滿負荷工作狀態，2表示染缸處于不滿負荷工作狀態；∑={不同缸容染缸工作事件的集合}，σi(i=1,2,…,l)表示第i種缸容的染缸滿負荷工作，βi、βj(i=1,…,l,j=1,…,l,i≠j)分別表示使第i種、第j種缸容的染缸不滿負荷工作，r表示染缸工作結束返回空閑狀態；δ:Q× ∑→Q為各種染缸工作狀態的轉移函數；表示l種染缸資源的初始狀態均處于空閑狀態；Qm為訂單順利加工完成后染缸的工作狀態。將染缸的工作視為一個事件，在自動機模型中，訂單的任何一種加工方式均可用一個事件串表示，這些事件串的集合可用正則表達式表示：R=(σlr)*…(σlr)*(βlr+…+βlr)，其中，∑c={σl,…,σl,βl,…,βl}，∑uc={r}。

2 訂單的最優染缸資源配置方式求解

假定各染缸滿負荷工作時利用率為100%，設有一組訂單，每個訂單的染缸分配過程按事件串長度分為n階段，定義以下5種關于染缸資源利用率的控制函數：

（1）在加工第p個訂單Np時，從第k階段到最后階段（第n階段）的染缸平均資源有效利用率函數為vk=(sk,uk)表示在第k階段，選取決策uk的染缸資源有效利用率；uk為在第k階段，當狀態處于sk時，對剩余訂單量分配染缸資源的決策函數。待各階段決策確定后，整個訂單染缸配置過程的決策序列就構成一個策略，用f={u1(s1),u2(s2),…,un(sn)}表示。

（3）對于訂單組中第p個訂單Np，當選取最優染缸配置方式后，染缸資源的實際利用率函數：Wp=Np/Mp，Np為第p個訂單的質量，Mp為所選各染缸的容量總和。

（4）對訂單組進行染缸資源配置后，整個訂單組加工周期符號表示對式子向上取整，P1080、P540、P360、P180、P50分別表示在染缸資源配置結果中缸容分別為1 080、540、360、180、50 kg的染缸使用次數。

在生產中，為了提高生產質量，需將訂單盡量分配在較大缸容染缸里加工一次，避免在較小缸容染缸里加工多次而出現色差問題，在此引入利用率折扣率ρ，用來降低訂單在較小缸容資源的使用頻率和效率。同時，為了將所有染缸投入生產，降低染缸閑置率，引入等待加工利用率折扣率g，用來降低訂單因排隊等待加工的染缸資源有效利用率，使訂單優先分配到運作次數較少的染缸加工。ρ與g的取值范圍都為（0，1）。本研究選取一組染缸容量為1 080、540、360、180、50 kg，相應機臺數矩陣X=[x1,x2,x3,x4,x5]，x1、x2、x3、x4、x5分別表示缸容為1 080、540、360、180、50 kg的現有機臺數。在此，定義以下兩個有效染缸資源利用率函數：

（1）在加工第p個訂單Np時，各染缸不滿負荷工作時染缸資源的有效利用率函數：

（2）在加工第p個訂單Np時，各染缸滿負荷工作時染缸資源的有效利用率函數為：

其中，λ1、λ2、λ3、λ4、λ5表示剩余訂單量在缸容為1 080、540、360、180、50 kg的染缸中不滿負荷工作時的染缸利用率。H矩陣為加工到各階段各類缸容染缸使用次數累計矩陣。將該算法經Matlab編譯并對大量訂單進行染缸資源配置，結果顯示，對于ρ和g的大小，若側重于訂單組質量問題，應將訂單盡量分配到大染缸中加工，減少加工次數，較好的系數取值范圍為0.80≤ρ≤0.85，0.90＜g≤1.00；若側重于單組加工時間問題，應盡快加工訂單，縮短訂單排隊等待加工時間，較好的系數取值范圍為0.80≤g≤0.85，0.90＜ρ≤1.00。

在染缸資源配置自動機模型中，每個訂單的每種加工方式都可以用一個事件串表示。將每個染缸工作一次視為一個事件，對訂單的染缸配置過程按事件串長度劃分階段，在每個階段設定染缸資源利用率為決策函數，并建立各個階段之間染缸資源利用率的遞推關系，最后以所用染缸的有效平均資源利用率最大為目標函數尋找訂單最優排缸策略。現有一訂單組質量分別為860、350、670、1 150、1 200、2 150 kg，將此訂單組分別用本研究所提算法與計劃員進行染缸資源配置，結果如表1所示。

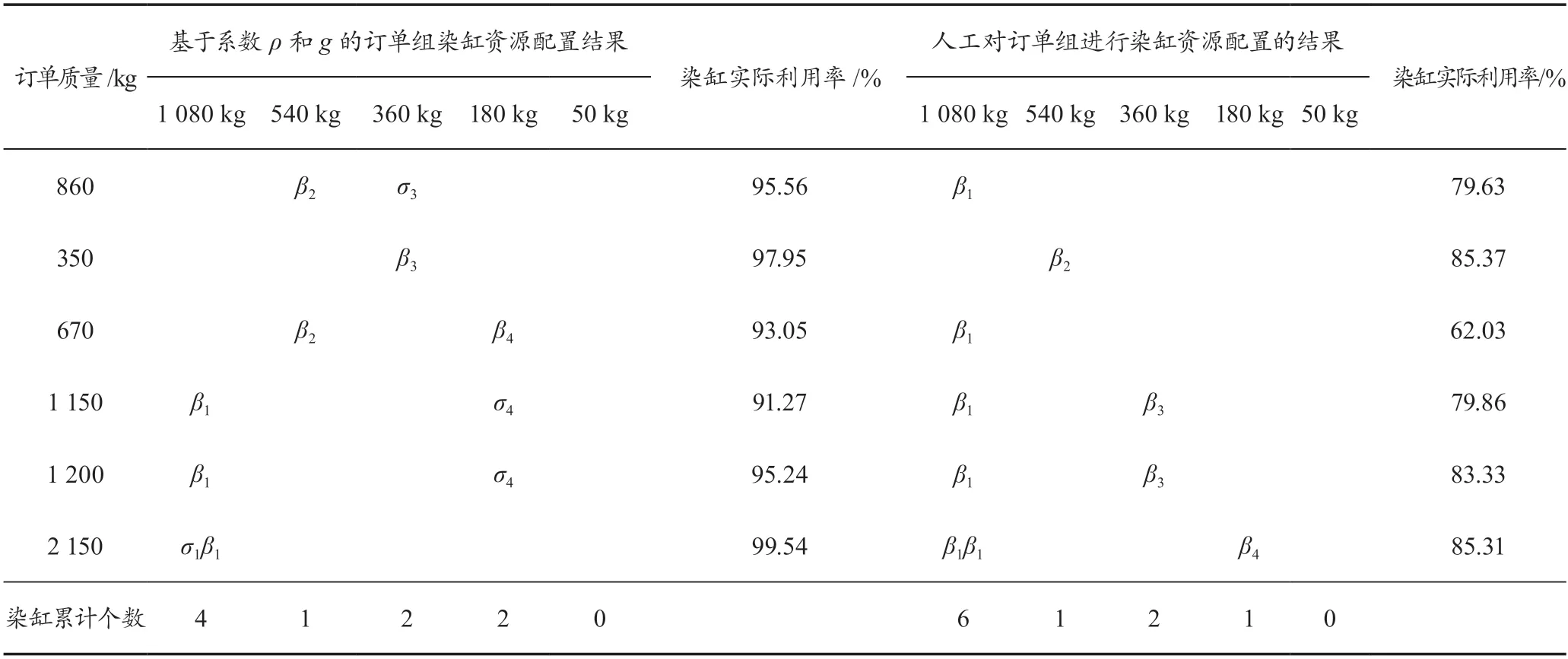
表1 本研究所提算法的排缸結果

分析表1可知，在基于折扣系數ρ和g的訂單組染缸資源配置結果中，整個訂單組的加工周期：

人工加工周期：

由以上計算分析可知，在基于系數ρ和g的訂單染缸配置結果中，訂單組為2個加工周期，與人工配置結果相比縮短了1個加工周期，且染缸資源利用率明顯提高。

3 結語

本研究將資源配置系統的自動機模型及動態規劃最優染缸配置方式應用于實際訂單的染缸資源配置中，配置結果與印染企業中的人工配置結果相比，各染缸閑置率較低，訂單組加工周期縮短，染缸利用率大幅提高，這對年產值數億元的印染企業來說意義深遠。折扣系數的取值范圍是結合實驗測試及人工經驗選擇的，有待進一步測定。