基于改進遺傳算法的配網自動化終端布點優化配置方案研究

夏磊 符瑞 智明 李珩

作者簡介：夏磊（1989-），高級工程師，從事配電自動化的研究。

通訊作者：李珩（1987-），高級工程師，從事配電自動化的研究，lilizy4901@126.com。

引用本文：夏磊，符瑞，智明，等.基于改進遺傳算法的配網自動化終端布點優化配置方案研究[J].化工自動化及儀表，2023，50（6）：000-000.

DOI：10.20030/j.cnki.1000-3932.202306000

摘? 要? 首先對配網自動化的可靠性指標進行闡述并建立數學模型，提出將遺傳算法用于解決復雜情況下的配網自動化終端布局優化，并將模擬退火算法的思想與傳統遺傳算法結合，最后用改進后的遺傳算法與普通遺傳算法對配網自動化終端布局優化進行了對比，驗證了改進后的遺傳算法的性能提升，并用改進后的遺傳算法求解復雜配網自動化終端布點優化。通過對改進后的遺傳算法求解得到的最優解進行解碼，得到的方案結果表明：優化后的配網自動化終端布局方案的供電可靠性提升到99.992%，并且方案所需費用比不進行任何優化的配網方案費用有所減少。

關鍵詞? 遺傳算法? 模擬退火算法? 供電可靠性? 配網自動化終端? 終端優化布局

中圖分類號? TP29? ? ? ? ? 文獻標志碼? B? ? ? ? ?文章編號? 1000-3932（2023）06-0000-00

從2009年開始，在國家的支持下電力企業為建設配網自動化開始投入大量資金[1]。當配網自動化的規模越來越大的時候，設計規劃人員必須要讓有限的資源實現系統的最優配置[2]。但是對于配網自動化終端設備的各種研究還不夠深入，在建設時由于缺乏相應的指導意見，規劃設計人員需要花費大量的時間和精力制定科學、經濟的規劃方案。

遺傳算法是模擬自然界生物在繁衍過程中發生基因遺傳和變異現象后得到的一種概率學仿生搜索算法，具有計算方便且收斂性能好的特點[3]。模擬退火算法是由小范圍搜索算法拓展得到的一種新的算法，主要特點是在理論上避免陷入局部最優[4]。由于基本遺傳算法具有在全局搜索上會提前陷入局部最優的缺陷，可先通過遺傳算法得到初始種群，然后再用模擬退火算法的相關準則進行優化，改進后的遺傳算法無論是在局部搜索還是全局搜索方面都有了良好的表現。

在上述背景下，筆者首先對集中式饋線自動化配電網進行可靠性評估研究，然后使用改進的遺傳算法提升其效率與性能，最后驗證配電自動化終端布局的可靠性和經濟性，在終端選址選型方面為電力規劃人員提供決策支持。

1? 理論概述與模型研究

1.1? 供電可靠性指標

供電可靠性指標用來評價配電區域的供電系統是否達到系統安全要求，常用指標有負荷點指標與系統指標，負荷點指標用來評估單個負荷點的供電安全要求，系統指標用于評估配電區域的供電可靠性[5]。

1.1.1? 負荷點的供電安全指標

負荷點的供電可靠性指標有負荷點年平均故障率、負荷點年平均故障持續時間U、負荷點每次故障導致的停電持續時間。

負荷點的年平均故障率指負荷點在一年時間內發生問題出現故障的次數；負荷點的年平均故障持續時間是負荷點在一年時間內運維發生故障，導致系統不能正常工作的時間。負荷點每次故障的停電持續時間計算式為：

tr=U/? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1）

1.1.2? 供電系統的可靠性指標

供電系統的可靠性指標主要有系統平均停電持續時間指標（System Average Interruption Duration Index，SAIDI）、平均供電可靠率指標（Average Service Availability Index，ASAI）、系統電量不足指標（Energy Not Supplied，ENS）、系統平均電量不足指標（Average Energy Not Supplied，AENS）[6]。計算式如下：

（2）

（3）

（4）

（5）

其中，m是負荷點總數，為負荷點i所接的用戶數，是負荷點i的年平均故障持續時間，為負荷點i所接的總平均負荷。

1.2? 遺傳算法

1.2.1? 遺傳算法的原理

遺傳算法（Genetic Algorithms，GA）是根據自然選擇學說里面的演繹進化規律得到的在全局進行搜尋的優化算法[7]。遺傳算法在優化過程中，搜索空間從大的范圍逐步縮小到小范圍的局部。通過一系列的進化和重組過程，最終得到在搜索范圍內的最優解，適用于復雜組合問題的優化求解[8]。遺傳算法的計算過程如圖1所示。

1.2.2? 遺傳算法的優缺點

GA作為一種隨機搜索算法，復雜的優化組合問題都可以用GA來解決[9]。由于模仿自然界生物基因遺傳變化，通過交叉和變異，使得GA相比于其他同類型的算法有著更加優異的搜索性能，可以更好地求解復雜的優化組合問題，主要表現為不限制搜索的空間、具有同步性、自適應性強、操作簡單及擴展融合能力強等。

因為GA算法的優異性能，它得到了越來越多的應用。在應用過程中，GA算法的缺點也暴露了出來，主要有需要選取的參數比較多、收斂速度慢、適應度函數建立不當會導致算法沒有進行全局搜索便提早找出局部最優解，這樣得到的解便失去了它的價值，限制了遺傳算法在某些問題和范圍上的求解能力。

為了更好地求解復雜組合優化問題，需要學者們對遺傳算法進行改進與融合，更大程度上發揮出GA的實際應用和研究價值。

1.3? 模擬退火算法

利用模擬退火算法尋找最優解，首先需要設定初始溫度，從初始溫度出發，計算出目標函數的初始值，然后結合溫度的跳突特性，目標函數會以一定的概率跳出局部最優解從而向全局最優解靠近。模擬退火算法的特性是可以在一定程度上接納劣解，然后通過跳突方式跳出局部，再繼續緩慢降溫，直至設定的最低溫度[10]。

模擬退火算法的計算過程如圖2所示。

需要注意的是，溫度函數會影響到模擬退火算法的求解能力，常選用最簡單的指數函數作為溫度函數，當系統的溫度下降到設定的閾值時，系統達到了新的穩定狀態，此時便得到了新的全局最優解。模擬退火算法的特點就是能在一定程度上接受質量比較差的解，并且得到的解不滿足系統要求的概率比較低。當系統的初始溫度設置得非常高時，選取合適的冷卻函數，理論上模擬退火算法便能保證高精度的同時又能避免只找到局部最優解[11]。

1.4? 基于模擬退火算法的改進遺傳算法

GA是在全部種群中通過隨機挑選進行搜索的方法獲得全局最優解，但對于復雜的優化組合問題，GA采用的隨機挑選進行搜索的方法存在提前找到局部最優解和搜索性能差的問題。經過分析發現，由于不同種群間的個體存在差異，在進行交叉的過程中可能會遺漏最佳解，即使已經非常靠近最佳解，仍然很難得到最佳解[12]。模擬退火算法在尋找小范圍最佳解時表現出了良好的性能。因此將模擬退火算法的思想應用在遺傳算法中，可以更加有效地解決實際問題。改進遺傳算法的流程如圖3所示。

改進后遺傳算法的收斂判據為：

a. 限定迭代次數，系統運算了限定的次數后停止計算；

b. 算法運行過程中，若個體適應度不再發生變化則停止操作；

c. 算法運行了一段時間，當算子種群的平均適應度小于算子最優個體適應度時，停止計算。

1.5? 基于改進遺傳算法的配網自動化終端

配網自動化終端布局的優化首先需要考慮到網架結構、線路數據、用戶分布及投資額等因素，其次要考慮在不同類型終端安裝在不同位置所帶來的效益提升的差異、建設成本和預估收益，經過綜合考慮后最終確定方案[13]。

配電系統中還需要考慮配電網的故障處理，需要著重考慮出線斷路器和聯絡開關，并且配電系統中有大量的分段開關，配電自動化終端安裝在不同的分段開關處，對供電系統的性能提升作用也不相同，難以準確地評估分段開關的重要性，因此需要重點研究分段開關終端優化的布局問題[14]。

1.5.1? 目標函數

為了研究配電自動化終端的優化布局，需要考慮負荷增長率的影響。將目標函數設為各項投資成本的現值之和，計算式如下：

（6）

其中，為運行設備的維護費用，是購買設備和安裝費用，計算式如下：

（7）

（8）

其中，為饋線集合；為饋線上分段開關位置的集合；=1表示饋線f上終端位置s處安裝了二遙終端，=0則表示對應位置沒有安裝二遙終端；=1是饋線f上的終端位置s處安裝了三遙終端，=0則表示對應位置沒有安裝三遙終端；為二遙終端的單價；為三遙終端的單價；為折現率；為設備維修占比；為規劃年限。

內部成本Cint的計算公式為：

（9）

其中，為第t年饋線f上第k段的故障發生率；為第t年饋線f上負荷點i處第j類點的平均負荷；為第t年饋線f上第k段發生故障時負荷點i處第j類負荷點的單位停電量導致的費用損失；為饋線分段集合；為負荷點的類點集合；為負荷點的集合。

1.5.2? 約束條件

終端安裝位置。二遙終端和三遙終端不能同時安裝在一個待選位置，所以終端安裝位置的約束為：

（10）

可靠性指標。終端安裝完成后，配電系統的可靠率水平要達到規劃文件的要求，所以配電系統的可靠率約束為：

（11）

其中，為改造后配電系統的平均供電可靠率指標值，是決策變量；為規劃文件要求區域最低供電可靠率；為饋線f上第k段發生故障時，第i負荷點的j類負荷的停電時間。

初試投資費用。購買安裝二遙、三遙終端的費用應當小于初始的投資金額F，即：

（13）

其中，是二遙終端的數量；是三遙終端的數量。

1.5.3? 模型求解流程

配電自動化終端優化布局的模型求解流程如圖4所示。

本節使用的算例系統為IEEE RBTS BUS4配電系統，算例系統結構如圖5所示。

2? 實驗測試與結果分析

2.1? 實驗設定

設定規劃年限為15年，系統運行維護費用占總投資額的4%，貼現率為9%，二遙終端單價是每組1萬元，三遙終端單價是每組4.7萬元，單位停電量損失是25 kW·h，負荷增長率是1.1%，人工故障排查速度設置為2 km/h。

改進的遺傳算法參數設置如下：

目標函數的G值? 1 000

初始溫度? 500

交叉概率? 0.1

變異概率? 0.8

最大迭代次數? 50

2.2? 改進后遺傳算法的驗證分析

為了驗證基于模擬退火算法的遺傳算法在求解終端布局優化問題的優越性，分別采用改進的遺傳算法和普通遺傳算法對終端布局優化問題進行求解，每種算法求解50次，算法的收斂曲線如圖6所示，求解結果見表1。

對所得最優解進行解碼還原出的優化結果見表2。

2.3? 不同方案的驗證結果分析

為了驗證配網終端優化布局的有效性，設計了4種方案進行驗證：

方案一。各分段開關處沒有安裝任何終端設備。

方案二。二遙終端安裝在各個分段開關處。

方案三。三遙終端安裝在各個分段開關處。

方案四。終端系統的供電可靠率設置為99.982%，將其作為終端布局過程中的可靠性約束，進行終端的優化布局。

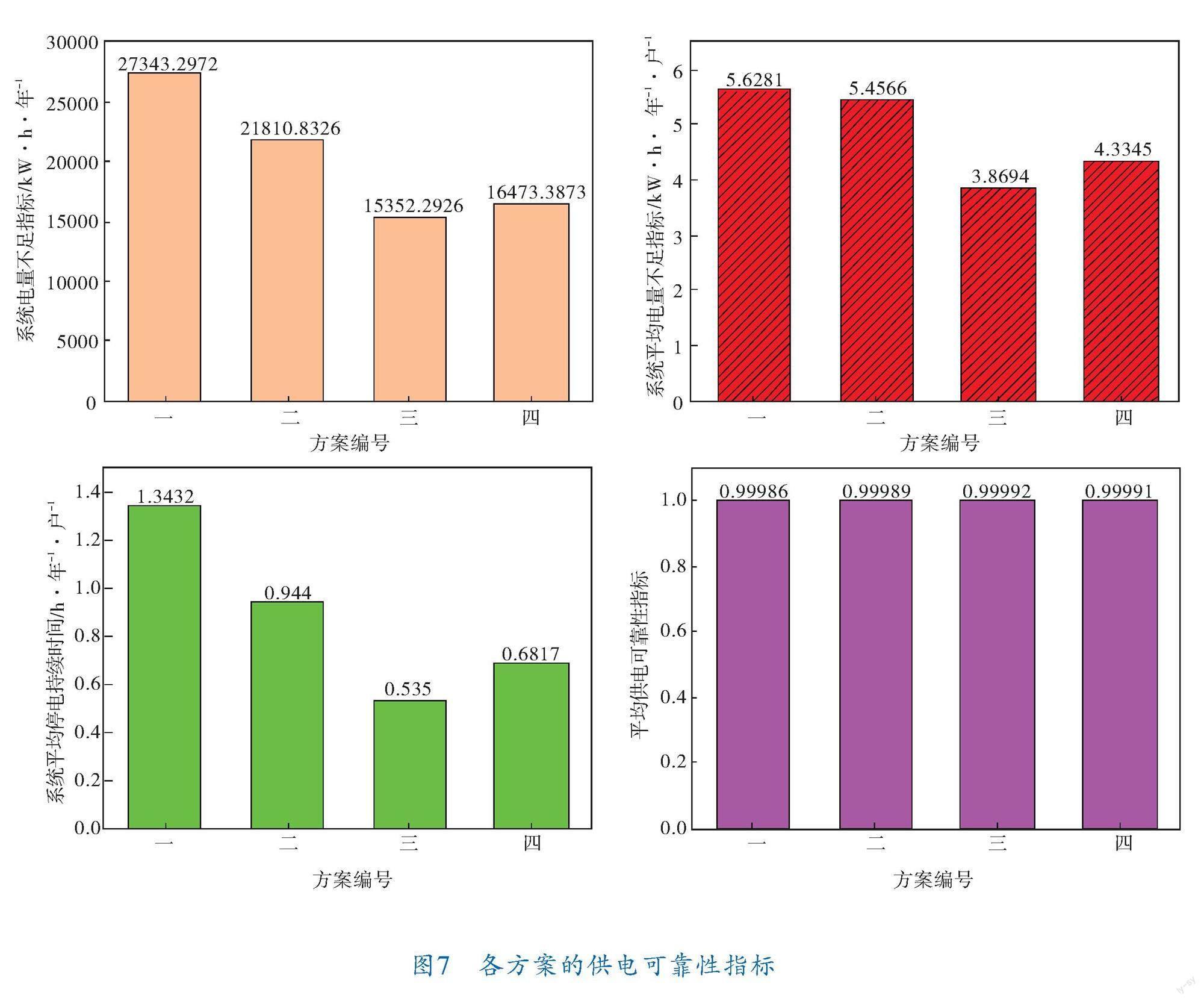
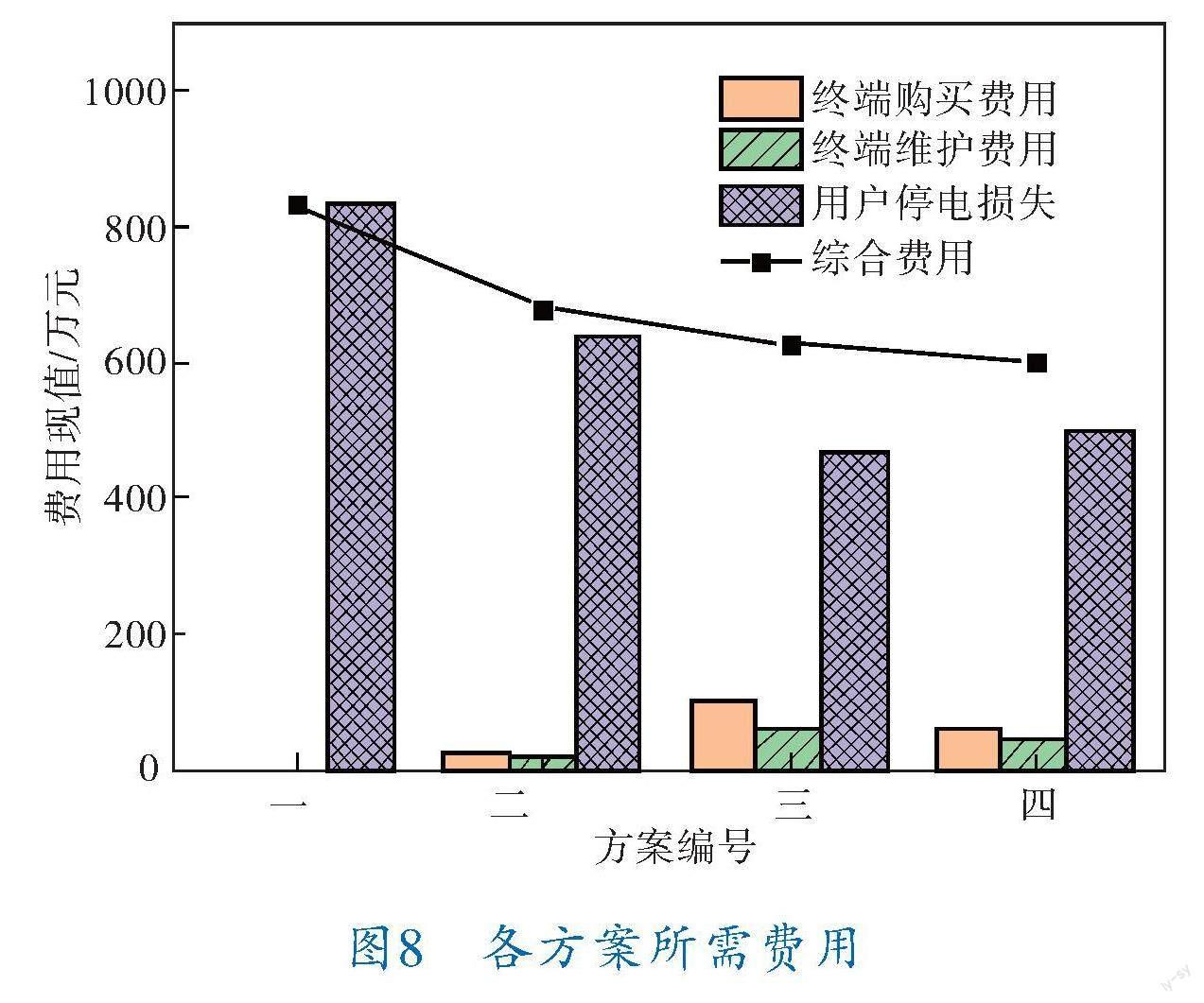
各方案結果如圖7、8所示。

由圖7、8可知，方案二、三、四的綜合費用遠低于方案一的，區域供電的可靠性顯著提升，減少的停電損失費用遠大于終端增加購買費用和運行設施維護費用。方案三的供電可靠性最高，但是方案三的三遙終端購買費用、維護成本也最高，經濟性不是很好；方案四的供電可靠性略低于方案三，但是方案四的綜合費用最低，既能達到供電可靠性的提升要求又能最大程度上節省投資成本，是兼顧了可靠性與經濟性的最佳方案。

3? 結束語

將模擬退火算法的思路運用于遺傳算法的改進，首先用GA選定初始種群后，用模擬退火算法對初始種群進行改良，然后進行相對應的交叉和編譯操作，改進后的GA可以在一定程度上接受不良解，從而避免了遺傳算法提前收斂只能找到局部小范圍的最佳解。在初始投資費用比較緊張的情況下，通過適當降低投資費用也可以得到綜合成本費用低但是性能表現良好的布局方案，但是過度降低初始投資費用會大幅增加綜合費用。還可以通過合理安排檢修來提高故障的排查速度，從而有效地減少投資費用并提升系統的可靠性。

所提出的改進遺傳算法相比于普通遺傳算法，表現出了良好的優化性能，但是全局尋優能力和收斂性上仍然有很大的提升空間，可以通過合適的方法進行改進。大量的分布式電源并網和負荷需求響應策略增加了配電網進行控制的難度，需要進一步研究分布式電源實時需求響應的配電供電可靠性評估過程和通信可靠性的影響。

參? 考? 文? 獻

[1]趙海波.電力行業大數據研究綜述[J].電工電能新技術，2020，39（12）：62-72.

[2]洪成，史俊霞.配網自動化系統在城市電網中的應用[J].上海電力大學學報，2021，37（S1）：47-48；52.

[3]KATOCH S，CHAUHAN S S，KUMAR V.A review on genetic algorithm：Past，present，and future[J].Multimedia Tools and Applications，2021，80（5）：8091-8126.

[4]FATHOLLAHI-FARD A M，GOVINDAN K，HAJIAGHAEI-KESHTELI M，et al.A green home health care supply chain：New modified simulated annealing algorithms[J].Journal of Cleaner Production，2019，240：118200.

[5]郭大鑫.基于供電可靠性的配電自動化系統規劃方法[J].電氣傳動自動化，2022，44（3）：13-16.

[6]YAN F，CHEN X Y，TANG W S，et al.Reliability and power supply capability evaluation of active distribution networks with four-terminal soft open points[J].IET Smart Grid，2020，3（5）：657-666.

[7]MIRJALILI S，DONG J S，SADIQ A S，et al.Genetic algorithm：Theory，literature review，and application in image reconstruction[J].Nature-inspired Optimizers，2020：69-85.

[8]王運濤，劉鋼，薛俊芳.基于改進遺傳算法的拆卸序列規劃[J].現代制造工程，2022（1）：137-142；136.

[9]MAYER M J，SZIL?GYI A，GR?F G.Environmental and economic multi-objective optimization of a household level hybrid renewable energy system by genetic algorithm[J].Applied Energy，2020，269：115058.

[10]王貴全，張錦榮，邵毅，等.基于透射光譜的類金剛石膜光學參數反演[J].紅外技術，2021，43（5）：473-477.

[11]KURTULU? E，YILDIZ A R，SAIT S M，et al.A novel hybrid Harris hawks-simulated annealing algorithm and RBF-based metamodel for design optimization of highway guardrails[J].Materials Testing，2020，62（3）：251-260.

[12]HAN J X，MA M Y，WANG K.Product modeling design based on genetic algorithm and BP neural network[J].Neural Computing and Applications，2021，33（9）：4111-4117.

[13]余文斌，王彬.配網自動化建設對供電可靠性的影響分析[J].光源與照明，2022（3）：231-233.

[14]汪旭，雪向兵.中壓環網配電開關充氣柜泄壓裝置的設計[J].新型工業化，2021，11（7）：23-24.

（收稿日期：2023-01-12，修回日期：2023-09-12）