壓縮sCO₂儲能系統動態特性仿真

摘要：壓縮超臨界二氧化碳（sCO2）儲能作為一種新型儲能方式，具有儲能密度大，結構緊湊，使用壽命長，負碳排放等優點，因此，在能源儲存轉化等方面有著廣闊的應用前景。基于質量守恒和能量守恒定律，建立了壓縮sCO2儲能系統（SC-CCES）的動態數學模型，并完成了模型可靠性的驗證；采用Matlab及Simulink軟件實現了單級壓縮和單級膨脹的SC-CCES系統動態特性仿真，設計工況下SC-CCES系統的儲能效率為51.98%，儲能密度為447.8 kWh/m3，其儲能密度是傳統壓縮空氣儲能系統儲能密度的20倍以上；分析了不同高壓儲罐入口壓力對系統性能的影響，結果表明儲能效率隨高壓儲罐入口壓力的增大而增大，儲能密度則恰好相反。此研究為壓縮二氧化碳儲能的發展提供了基礎。

關鍵詞：壓縮超臨界二氧化碳儲能；動態仿真；能量守恒；儲能密度

中圖分類號：TK02"" 文獻標志碼：A"" 文章編號：1002-4026（2024）04-0093-12

開放科學（資源服務）標志碼（OSID）：

Study on supercritical carbon dioxide energy storage system

and its operating characteristics

JIANG Jiahui1，WANG Zijie2，CHI Ran2，CHEN Wei1，XUE Xiaodai3，

ZHANG Tong3，ZHANG Xuelin3，ZHANG Bin1*

（1.College of Electromechanical Engineering，Qingdao University of Science amp; Technology，Qingdao 266061， China；

2.Power China Hebei Electric Power Engineering Co.， Ltd.， Shijiazhuang 050000， China；

3.Department of Electrical Engineering，Tsinghua University，Beijing 100084， China）

Abstract∶As a novel energy storage method， compressed supercritical carbon dioxide （sCO2） energy storage offers several advantages， such as high energy storage density， compact structure， long service life， and negative carbon emissions. Therefore， it has a broad application prospect in the energy storage and conversion. In this study， a dynamic mathematical model for the compressed sCO2 energy storage system （SC-CCES） was established based on the mass conservation and energy conservation laws and the reliability of the model was verified. Additionally， dynamic simulations of the SC-CCES system with single-stage compression and single-stage expansion were performed using Matlab/Simulink. Under the designed operating conditions， the energy storage efficiency of the SC-CCES system was found to be 51.98%， with an energy storage density of 447.8 kWh/m3. The energy storage density of the SC-CCES system was more than 20 times higher than that of a traditional compressed air energy storage system. Furthermore， the impact of different high-pressure tank inlet pressures on system performance was analyzed. The results showed that the energy storage efficiency increases with the increase of the inlet pressure of the high-pressure storage tank， while the energy storage density is exactly the opposite. This study provides a basis for the development of compressed carbon dioxide energy storage.

Key words∶compressed supercritical carbon dioxide energy storage;dynamic simulation;energy conservation;energy density

近年來世界能源需求量的增加和化石能源造成的環境污染日益嚴重，因此大力發展可持續能源建設，構建減碳、零碳、負碳的新式能源體系已成為我國能源建設的重要目標。如今風能和太陽能已發展為頗具規模的可再生能源發電技術。然而，風電、光電具有間歇性、波動性和隨機性的特點，影響了電網的電能質量和運行穩定性［1］。解決這一問題的有效方法便是發展儲能技術。

目前，世界上能成熟應用的大規模儲能技術主要是抽水儲能（PHS）和壓縮空氣儲能（CAES）兩種。PHS難以擺脫地理條件的約束，且初始投資成本高，建設時間長，長期來看無法滿足儲能需求。而傳統的CAES依賴化石燃料的補充，依然會對環境造成污染。為了解決上述問題，人們開發了絕熱壓縮空氣儲能 （A-CAES）［2］、液態空氣儲能（LAES）［3］、超臨界壓縮空氣儲能（SC-CAES）［4］等系統，以提高儲能密度和系統效率。但是，空氣的臨界密度較低，導致壓縮空氣儲能的密度偏低［5］。

sCO2（超臨界二氧化碳）具有良好的熱穩定性、無毒、不燃燒，且具有更高的臨界密度，因此使用sCO2作為壓縮氣體儲能的介質將能夠大幅提升系統的儲能密度。同時，壓縮sCO2儲能系統實現了CO2的資源化利用，是一種非常具有潛力的儲能方式［6］。

主流的壓縮CO2儲能技術主要有跨臨界CO2系統（TC-CCES）、超臨界CO2系統（SC-CCES）和液態CO2系統（LCES）。郝銀萍［7］針對TC-CCES系統進行了穩態性能仿真，研究了TC-CCES系統的穩態熱力學特性和經濟性。宋飄飄［8］提出了一種半封閉式的SC-CAES系統，并通過仿真模擬研究了系統循環參數和循環形式對穩態循環性能的影響。Wang等［9］提出了一種液態二氧化碳儲能系統，并且研究了關鍵參數對系統性能的影響。LCES由于儲冷設備和儲冷效率的限制，尚無法實現工程應用。前期研究表明TC-CCES和SC-CCES系統具有優良的儲能特性，但是，目前絕大多數的研究均是基于設計工況的穩態特性研究，鮮有關于CCES的動態特性仿真研究。

基于當前研究現狀，我們建立了SC-CCES系統的動態仿真數學模型，并對數學模型進行了可靠性驗證。基于動態特性仿真，研究了SC-CCES系統的瞬態運行特性，準確計算了儲能系統的儲能效率和能量密度，且將SC-CCES系統的儲能密度與壓縮空氣儲能系統進行了對比。

1 SC-CCES系統

圖1顯示的是SC-CCES系統原理圖。該系統由低壓儲罐（LST）、壓縮機（C）、換熱器（X、R）、高壓儲罐（HST）、汽輪機（T）、冷罐（COT）、熱罐（HOT）構成。系統運行分為儲能過程和釋能過程。

儲能過程：低壓儲罐中的sCO2經過由外部電源供電的壓縮機壓縮，得到高溫高壓的sCO2，再經由換熱器X降溫后通入高壓儲罐中，換熱器X中的導熱油吸收熱量后進入熱罐中儲存熱量，電能轉換為sCO2的勢能和導熱油的熱能。

釋能過程：高壓儲罐中的sCO2經過換熱器R加熱后變為高溫高壓的工作流體，流體進入汽輪機做功發電，sCO2的壓力溫度下降，進入低壓儲罐中保存，勢能和熱能轉化為電能輸出，至此循環完成。

2 數學模型

2.1 模型假設及符號定義

為建立SC-CCES系統的動態數學模型，我們采用如下合理的假設：

（1）所有壓縮、膨脹過程都是絕熱的，壓縮機的設計絕熱壓縮效率為0.8，汽輪機的絕熱效率為0.9；

（2）忽略壓縮機、儲氣罐、換熱器等設備中的熱損失；

（3）忽略換熱器的熱慣量，換熱器工況能夠快速達到穩態；

（4）壓力損失與CO2的質量流量成正比；

（5）CO2作為實際氣體處理，CO2的物性通過調用REFProp軟件參數實現。

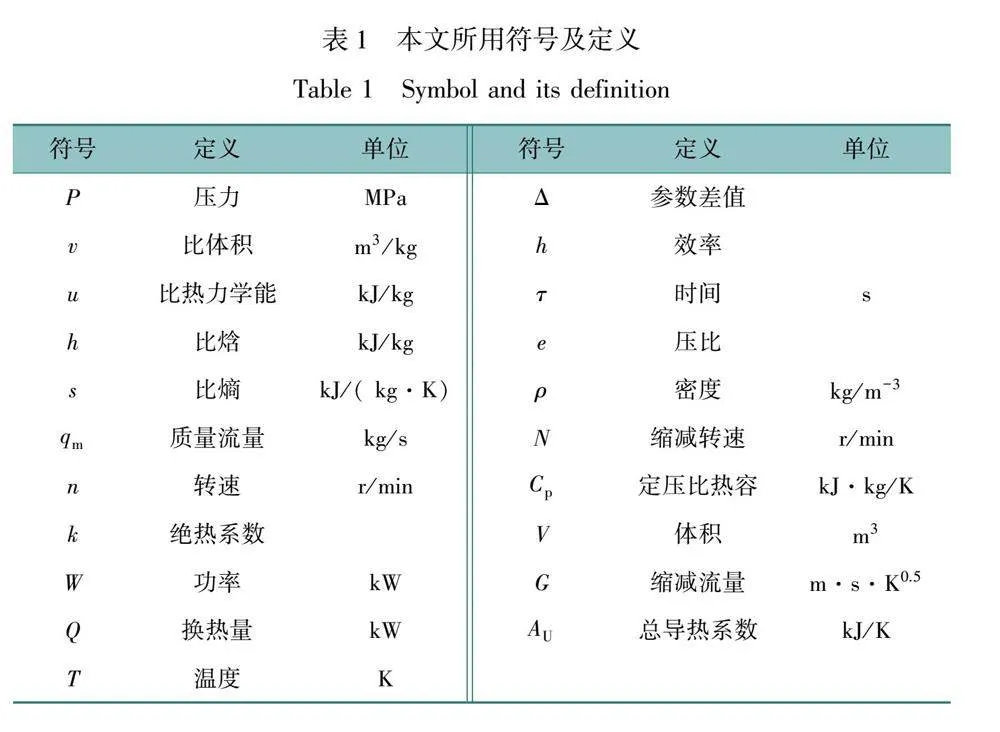
本文所用符號及定義如表1所示。文中上標·表示相對參數，下標0表示設計參數，下標1，2，…，9表示狀態點，下標oil表示導熱油，下標in表示入口參數，下標out表示出口參數，下標C表示壓縮機，下標T表示汽輪機。

2.2 模型建立

2.2.1 離心式壓縮機

壓縮機的瞬時功率W計算公式如下：

W=qm，CCpTεCk－1k－1ηC，（1）

離心式壓縮機的εC、ηC、nC具體計算模型如下［10］：

ε·C=c1（n·C）G·C2+c2（n·C）G·C+c3（n·C），（2）

η·C=［1－c4（1－n·C）2］（n·C/G·C）（2－n·C/G·C），（3）

c1=n·C/［q（1－m/n·C）+n·C（n·C－m）2］，（4）

c2=（q－2mn·C2）/［q（1－m/n·C）+n·C（n·C－m）2］，（5）

c3=－（qmn·C－m2n·C3）/［q（1－m/n·C）+n·C（n·C－m）2］，（6）

c4=0.3，（7）

G·C=GC/GC，0 ，GC=（qm，CTin）/Pin，（8）

n·C=NC/N0 ，"" NC=nC/Tin，（9）

ε·C=εC/εC，0 ，η·C=ηC/ηC，0，（10）

其中，c1、c2、c3、c4為中間參數；對于離心式壓縮機c4設為0.3，q和m分別為1.8。

2.2.2 儲氣罐模型

儲氣罐采用集總參數法進行動態建模，建模過程中忽略儲氣罐與環境之間的換熱。儲氣罐的質量守恒和能量守恒方程如下［11-12］：

Vdρdτ=qm，（11）

Vd（ρu）dτ=Vρdudτ+Vudρdτ=qmh。（12）

2.2.3 汽輪機模型

根據熱力學理論，汽輪機能量交換的過程為絕熱過程，瞬時功率如下：

W=qm，TCpTηTεTk－1k－1，（13）

汽輪機的εT、ηT、nT具體計算模型如下［13］：

G·T=1.4－0.4n·TεT－2－1εT，0－2－1，（14）

η·T=1－0.3（1－n·T）2（n·T/G·T）（2－n·T/G·T），（15）

G·T=GT/GT，0""""" ， GT=qm，TT/Pin，（16）

n·T=NT/NT，0""""" ， NT=nT/Tin，（17）

ε·T=εT/εT，0 ， η·T=ηT/ηT，0。（18）

2.2.4 換熱器模型

換熱器的熱慣量忽略不計，換熱器處于穩定狀態，以換熱器X為例，其能量平衡如下［14］：

QX=qm，CO2（hin，CO2－hout，CO2）=qm，oil，XCp，oil（Tout，oil－Tin，oil），（19）

上式中QX為換熱器的換熱量，QX可由下式計算得出：

QX=（AU）XTin，oil+Tout，oil－Tin，CO2－Tout，CO22，（20）

（AU）X為換熱器的總導熱系數［15］，總導熱系數與二氧化碳流量的關系如下：

（AU）X（AU）0=qm，CO2qm，CO2，0。（21）

為更好評估系統，采用以下指標來評估系統性能。

儲能效率［16］：

ηs=WTWC×100%。（22）

儲能密度：

Ds=WTVLST+VHST。（23）

2.3 模型驗證

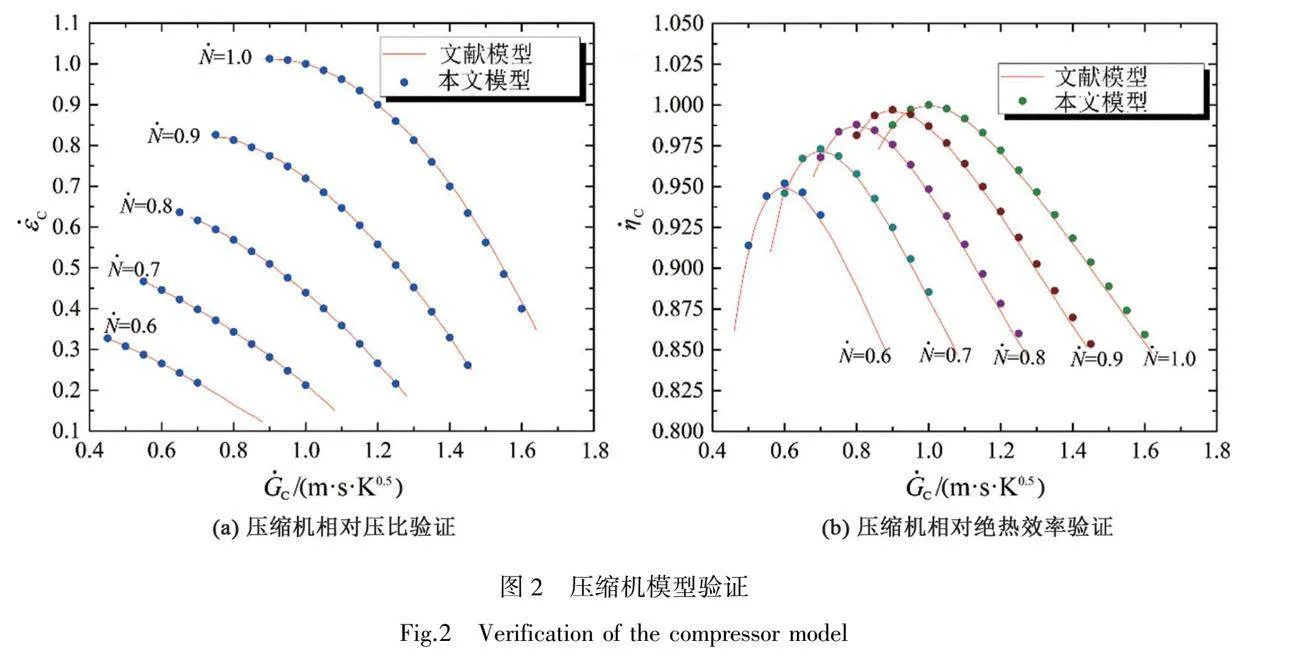
為確保所建模型的穩定性與精確度，我們針對壓縮機、汽輪機、儲氣罐進行了模型驗證。壓縮機模型驗證［17］如圖2所示，圓形符號表示由本文壓縮機模型計算出的穩態參數，紅線表示由文獻［17］中穩態模型計算出的穩態參數。由圖可知，研究建立的單級離心壓縮機動態仿真模型得到的穩態運行特性與文獻報道的數據一致，最大誤差不超過0.5%。結果表明，該壓縮機模型是可靠的。

圖3為汽輪機模型與文獻模型［18］的參數對比。藍色圓圈符號表示該模型計算出的穩態參數。紅線表示文獻穩態參數。結果表明，我們提出的模型計算的相對膨脹比和相對縮減效率與文獻模型計算的值基本相等，相對偏差不足0.1%。結果表明，該汽輪機模型是可靠的。

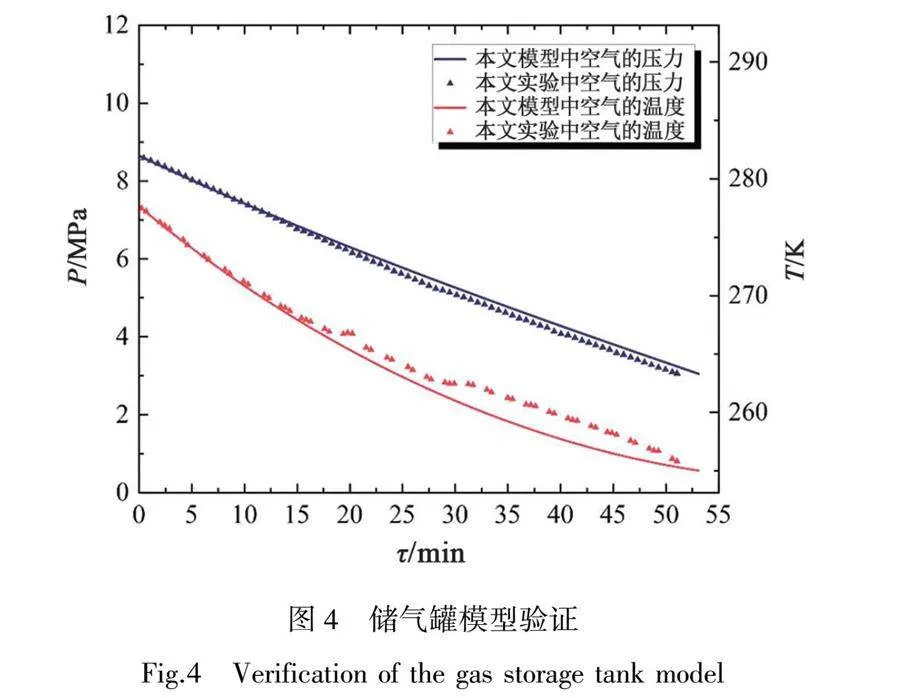
圖4為儲氣罐動態模型與文獻［19］實驗的參數對比。進氣放氣過程僅有進出口差別，因此只對放氣過程進行模型驗證。藍色和紅色線分別為儲氣罐內空氣的壓力和溫度的變化，三角符號為文獻［19］實驗所測的溫度壓力的變化。模擬結果與實驗偏差可歸因于實驗過程中換熱系數與環境溫度的變化。結果表明，本文建立的動態儲氣罐模型是可靠的。

3 運行結果分析與討論

3.1 設計工況

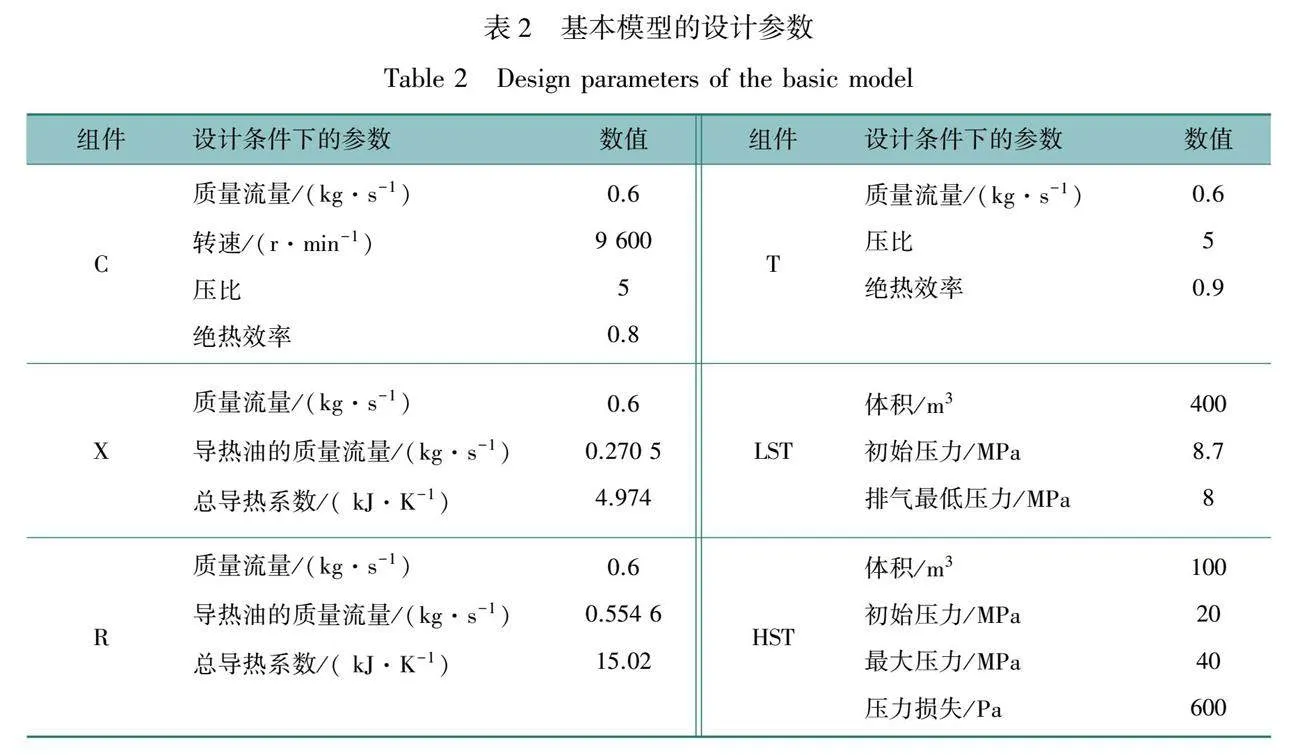
表2給出了系統模型的基本設計參數。

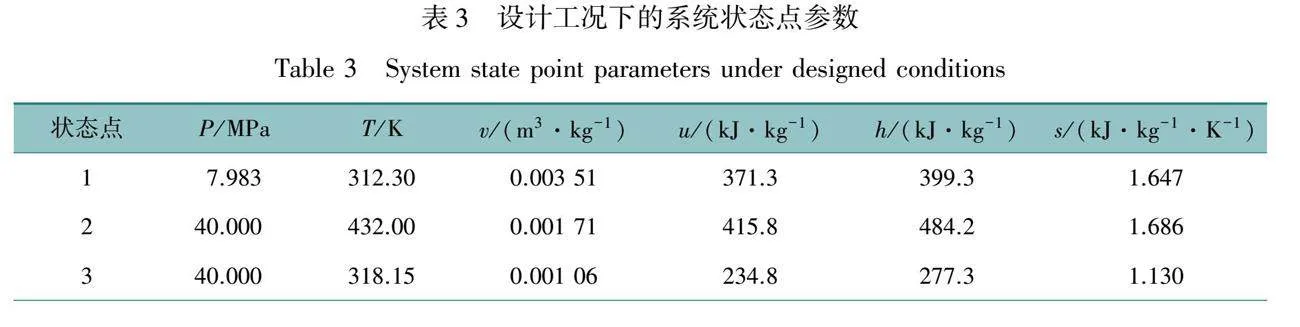
表3給出了設計工況下的狀態點參數。狀態點1～6為sCO2的熱力學狀態參數，其中從狀態點5和狀態點6可以看出sCO2的溫度壓力均下降，其比熵值不降反而略微升高，這是由于此次模擬將CO2當作實際氣體處理，所以其比熵并非為溫度的單值函數。狀態點7至9為導熱油的狀態參數。狀態點7為導熱油的初始狀態，規定其比熵值為0，初始溫度為298.15 K。導熱油在運行過程中比體積變化極其微小，因此將其視為定值。

設計工況下SC-CCES系統的熱力過程如圖5所示。壓縮儲能過程中，LST中的sCO2初始溫度為318.15 K，而經過狀態點1時溫度降為312.3 K，這歸因于sCO2具備的內能轉化為推動功，使其溫度降低。之后經過壓縮機壓縮，sCO2的壓力升至40 MPa，溫度升至432 K，壓縮機輸入的機械能轉化為sCO2的勢能與熱能，在此過程中sCO2的比體積減小，比熵值增大。壓縮完成后的sCO2經過換熱器X進行降溫，由表2看出sCO2的比焓、比熵值降低，能量通過熱傳導的方式傳給導熱油，使導熱油的溫度由298.15 K升至383.3 K，換熱后的導熱油匯入熱罐，完成熱能的存儲。降溫后的高壓低溫的sCO2進入HST中儲藏，儲能過程完成后HST的溫度升至336.2 K，這是由于sCO2的推動功轉化為內能，導致其溫度升高，比焓、比熵值上升。

釋能過程中，儲存在HST中的sCO2在釋能過程經由換熱器R加熱，使其溫度升高至377.3 K，比焓、比熵也隨之升高。相反導熱油的能量傳至sCO2使自身溫度降低至328.9 K，低溫狀態下的導熱油匯入冷罐中等待下一次循環。加溫后的高溫高壓sCO2進入汽輪機中做功，壓力勢能和熱能耦合利用，產生電能供給電網。做功后的sCO2溫度降至319.2 K，壓力降至8.7 MPa，比熱力學能與比焓值下降，而比熵值上升，這與sCO2的性質有關。做功后的sCO2進入LST中儲存以便下一次循環。在整個熱力學過程中，二氧化碳始終保持在超臨界狀態。

3.2 熱力學第一定律分析

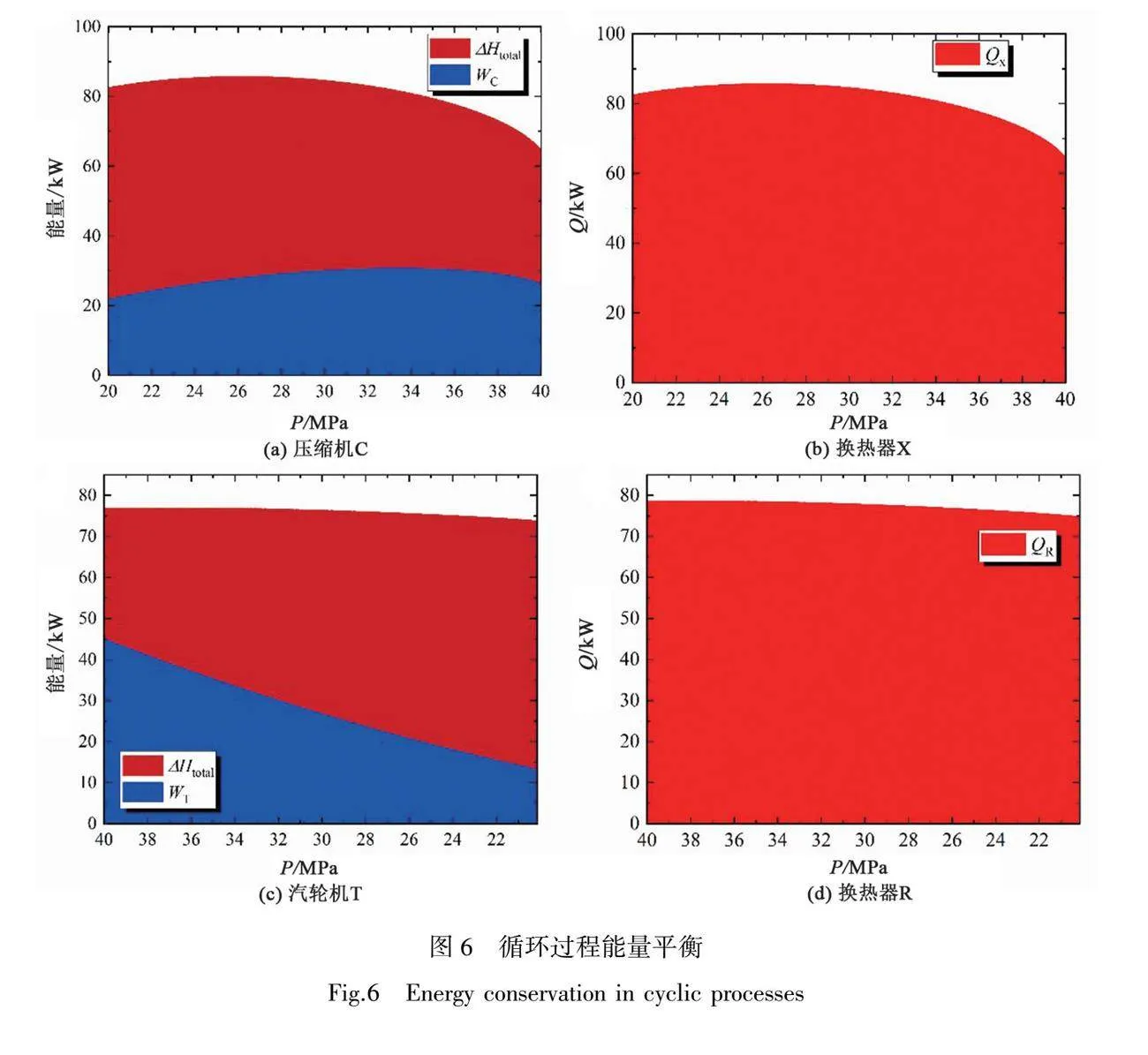
表4和表5給出了設計工況下儲能終了時刻和釋能初始時刻的系統能量守恒。在P4為40 MPa時壓縮機輸入能量為26.54 kW，換熱器X輸出能量為64.68 kW，sCO2的焓差（ΔHtotal）為38.13 kW，誤差在合理范圍內；在P4為20 MPa時換熱器R輸入能量為74.78 kW，汽輪機輸出能量為13.50 kW，sCO2的焓差（ΔHtotal）為61.28 kW，能量輸入輸出值相等。由此得出，所提出的動力模型在此兩時刻符合熱力學第一定律。

圖6（a）表示系統各時刻壓縮機壓縮功和儲能過程sCO2焓差的變化；圖6（b）表示各時刻換熱器X換熱量的變化；圖6（c）表示各時刻汽輪機的膨脹功和釋能過程sCO2焓差的變化；圖6（d）表示各時刻換熱器R換熱量的變化。由表4和圖6可得，我們構建的系統在動態仿真過程中遵循熱力學第一定律。

由圖6（a）可知儲能過程的ΔHtotal與WC均呈現先上升后下降趨勢，這是因為sCO2焓值的變化正是由壓縮機的壓縮功引起的，壓縮功的變化必然會導致sCO2焓差發生相應變化。圖6（a）與圖6（c）對比可知：釋能過程，WT變化較WC相對劇烈，但ΔHtotal變化則相對平穩，這與兩過程的壓力、溫度變化有關，儲能過程壓力、溫度變化較為劇烈，而釋能過程則相對平緩。由圖6（b）與圖6（d）對比可知：儲能過程QX呈現先升后降的趨勢，而QR則緩慢下降，這是因為QX的動態特性很大程度上受壓縮機的影響，且換熱器X的換熱溫度范圍較大，也會影響換熱量的變化。

系統循環過程中壓縮機總耗功為430.8 MJ，汽輪機做功223.9 MJ。換熱器X的累計換熱量為1 231 MJ，換熱器R為679.4 MJ。系統在設計點運行時，儲能效率為51.98%，儲能密度為447.8 kWh/m3。傳統壓縮空氣式儲能的儲能密度為2～20 kWh/m3［20］。由此可見SC-CCES系統儲能密度是CAES的20倍以上。

3.3 高壓罐入口壓力對系統性能的影響

高壓儲罐入口壓力對系統性能的影響如圖7所示。隨著高壓儲罐入口壓力的升高，ηs逐漸升高而Ds則逐漸降低。Ds的降低歸因于高壓儲罐入口壓力的提高，使得儲罐中儲存的sCO2質量減少，溫度降低，做功能力減弱而閉式系統儲氣容積不變，導致Ds逐漸降低。雖然汽輪機做工減少會導致ηs下降，但由于高壓儲罐入口壓力的提高導致壓縮機耗功降低更為劇烈，因此系統整體ηs不降反升。

3.4 SC-CCES系統的動態特性

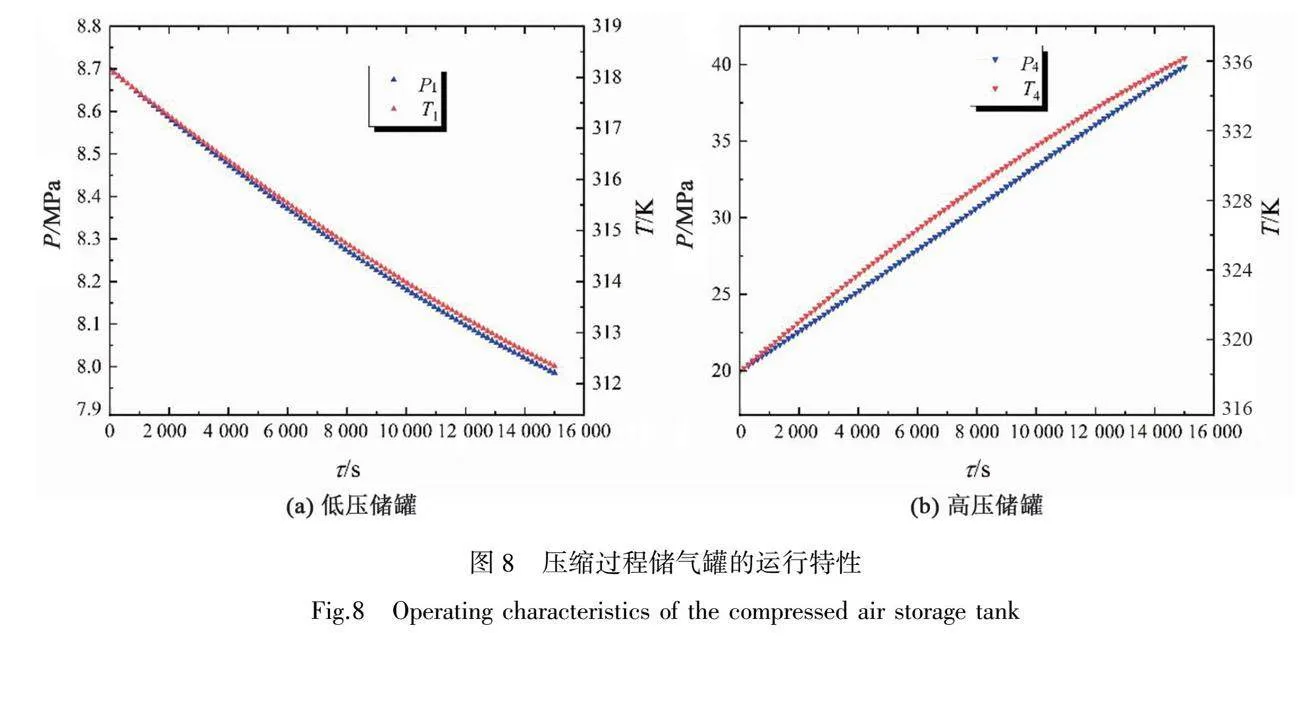
系統儲能過程低高壓儲氣罐的運行特性如圖8所示。低壓儲罐的溫度壓力呈單邊下降趨勢，而高壓儲罐則正好相反。隨著壓縮過程的進行，低壓儲罐中的sCO2經過壓縮機、換熱器X進入高壓儲罐，這導致低壓儲罐中的sCO2含量逐漸減少。隨著sCO2含量的減少低壓儲罐中的壓力從8.700 MPa降低至7.983 MPa，溫度從初始的318.15 K降低至312.3 K，這是由于sCO2的內能轉化為推動功使其溫度下降。相反高壓儲罐中的sCO2含量逐漸增多，導致其壓力從20 MPa升高到40 MPa，溫度也從318.15 K升至336.2 K，但在10 000 s附近趨勢變化略有減緩。這是因為在壓縮過程中進入高壓儲罐的sCO2的焓轉化為整個儲罐的sCO2的內能，當壓縮時間短，儲罐內的sCO2含量少，因此入口焓引起的溫升變化較大。而隨著壓縮時間變長，儲罐內sCO2含量升高，入口焓引起的溫升就會減慢。

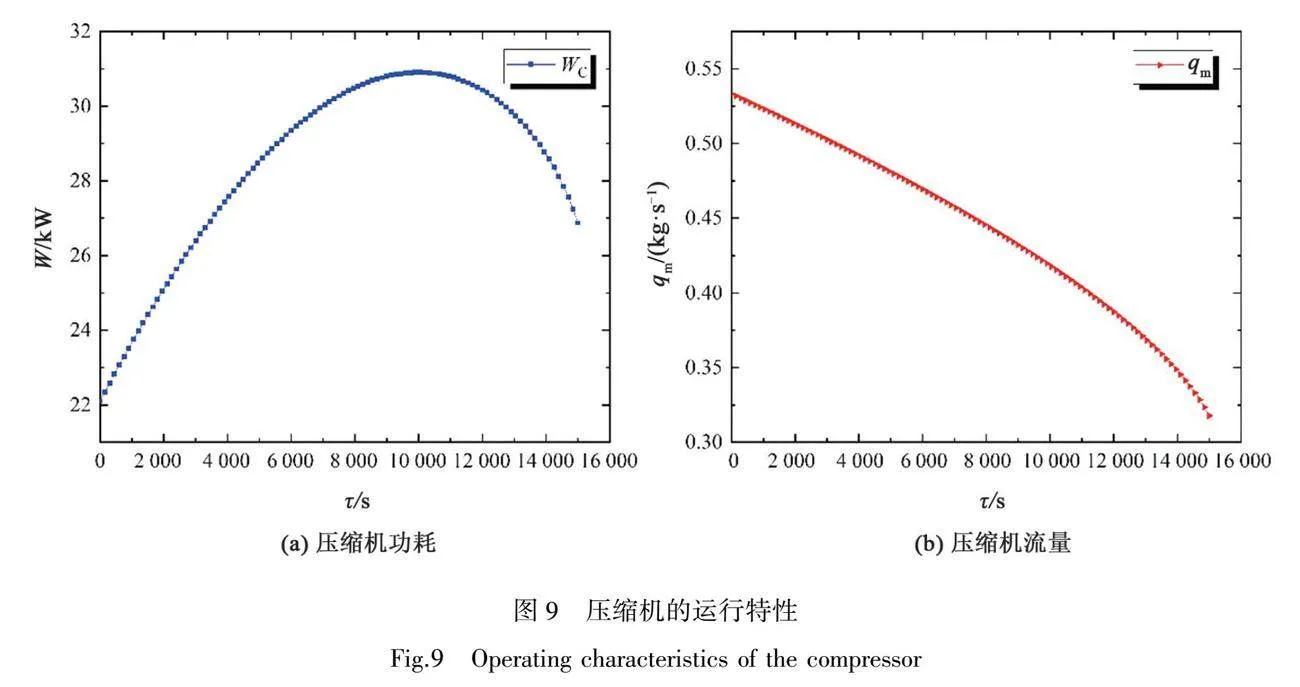
系統壓縮機的運行特性如圖9所示。在圖9（a）中，WC呈現先上升后下降的趨勢，始末值分別為22.1 kW和26.5 kW，峰值出現在10 000 s附近，為30.9 kW。在圖9（b）中qm，C呈現單邊下降的趨勢，起始值分別為0.53 kg/s和0.32 kg/s，在10 000 s附近開始呈現加速下降的趨勢。在壓縮開始時，壓縮機的壓比迅速上升，導致WC的增加，而在10 000 s左右通過壓縮機的qm，C呈現加速下降的趨勢，從而導致WC的下降。在此系統中壓縮機的功耗前期主要受壓比的影響，后期主要受qm，C的影響。

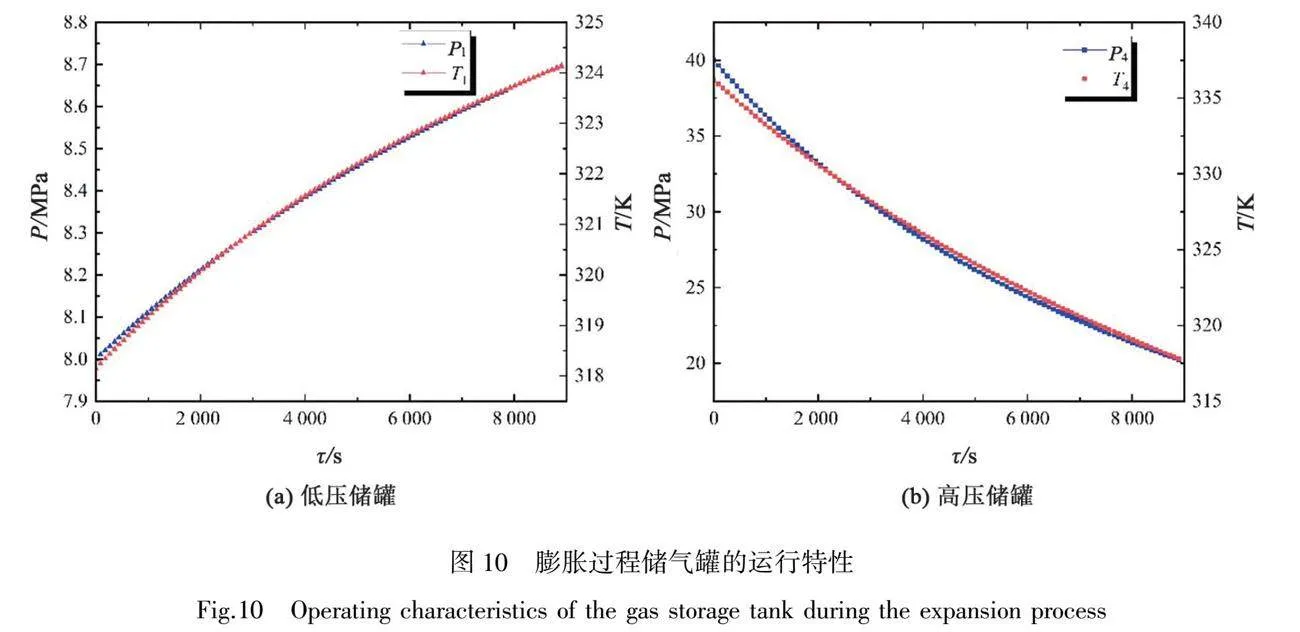
系統釋能過程低高壓儲氣罐的運行特性如圖10所示。與圖8給出的情況正好相反，高壓儲罐中的sCO2經過換熱器R、汽輪機進入低壓儲罐，這導致高壓儲罐中的sCO2含量降低。隨著sCO2含量的降低，高壓儲罐中的壓力從40 MPa降至20 MPa，溫度從336.2 K降至317.7 K，這同樣是由于sCO2的內能轉化為推動功。而低壓儲罐的溫度和壓力由于sCO2含量的增加分別增至324.2 K和8.7 MPa。由于釋能過程的時間短于儲能過程，而閉式系統溫度壓力范圍變化大致相同，所以釋能過程儲氣罐內的變化相對劇烈。

系統汽輪機的運行特性如圖11所示，在圖11（a）中，功率呈現單邊下降的趨勢，始末值分別為45.4、13.6 kW。在圖11（b）中，流量的變化趨勢功率相同，始末值分別為1、0.5 kg/s，二者的變化均為初始時刻較為劇烈，隨著時間的推移而逐漸平緩。WT下降歸因于汽輪機εT、qm，T下降使其偏離設計工況：釋能開始時，高低壓儲罐壓力差相對較高，汽輪機εT為5、qm，T為1，二者較高，汽輪機功率較高；而隨著時間的推移，高壓儲罐壓力降低，低壓儲罐壓力升高，汽輪機εT、qm，T等降低，致使功率降低。在釋能結束時，汽輪機εT為2.3，qm，T為0.5，二者數值最小，大幅偏離設計工況，使汽輪機瞬時功率最小。

4 結論

通過數值模擬的方法，建立了SC-CCES的動力學模型，對該模型進行了熱力學第一定律的分析，并仿真獲取了其動態特性，主要結論如下：

（1） SC-CCES系統在運行過程中符合熱力學第一定律。換熱器是能量輸入、輸出最大的部件且QX變化較QR而言更為劇烈，QX的變化受壓縮機影響較大。

（2） 設計工況下SC-CCES系統儲能效率為51.98%，儲能密度為447.8 kWh/m3，該系統儲能密度是傳統CAES的20倍以上。隨著高壓儲罐入口壓力的提高，系統儲能效率逐漸升高，儲能密度逐漸下降，二者呈相反趨勢。

（3） 儲能過程中WC呈先升后降趨勢，壓縮機流量qm，C呈單邊下降趨勢。儲能前期由于壓縮機壓比逐漸增大，WC隨其增大，在10 000 s附近達到峰值。后期由于qm，C的下降使WC加速下降。釋能過程中WT與qm，T均呈單邊下降趨勢。釋能初始時，高壓儲罐壓力大，膨脹比高，致使汽輪機WT高。而隨著時間的推移，高壓儲罐中的壓力、汽輪機膨脹比、qm，T等降低使WT降低。

參考文獻：

［1］張浩. 風電功率時空不確定性預測方法研究［D］. 北京： 華北電力大學， 2021.

［2］CHEN L X， WANG Y Z， XIE M N， et al. Energy and exergy analysis of two modified adiabatic compressed air energy storage （A-CAES） system for cogeneration of power and cooling on the base of volatile fluid［J］. Journal of Energy Storage， 2021， 42： 103009. DOI： 10.1016/j.est.2021.103009.

［3］XUE X D， WANG S X， ZHANG X L， et al. Thermodynamic analysis of a novel liquid air energy storage system［J］. Physics Procedia， 2015， 67： 733-738. DOI： 10.1016/j.phpro.2015.06.124.

［4］GUO H， XU Y J， CHEN H S， et al. Thermodynamic characteristics of a novel supercritical compressed air energy storage system［J］. Energy Conversion and Management， 2016， 115： 167-177. DOI： 10.1016/j.enconman.2016.01.051.

［5］吳毅， 胡東帥， 王明坤， 等. 一種新型的跨臨界CO2儲能系統［J］. 西安交通大學學報， 2016， 50（3）： 45-49. DOI： 10.7652/xjtuxb201603007.

［6］FU L P， REN Z K， SI W Z， et al. Research progress on CO2 capture and utilization technology［J］. Journal of CO2 Utilization， 2022， 66： 102260. DOI： 10.1016/j.jcou.2022.102260.

［7］郝銀萍. 跨臨界壓縮二氧化碳儲能系統熱力學特性及技術經濟性研究［D］. 北京： 華北電力大學， 2021.

［8］宋飄飄. 半閉式超臨界二氧化碳循環性能分析［D］. 北京： 華北電力大學， 2021.

［9］WANG M K， ZHAO P， WU Y， et al. Performance analysis of a novel energy storage system based on liquid carbon dioxide［J］. Applied Thermal Engineering， 2015， 91： 812-823. DOI： 10.1016/j.applthermaleng.2015.08.081.

［10］GUO H， XU Y J， ZHANG Y， et al. Off-design performance and an optimal operation strategy for the multistage compression process in adiabatic compressed air energy storage systems［J］. Applied Thermal Engineering， 2019， 149： 262-274. DOI： 10.1016/j.applthermaleng.2018.12.035.

［11］龐碩. 先進絕熱壓縮空氣儲能系統部件特性分析及優化設計［D］. 北京： 華北電力大學， 2019.

［12］周倩. 壓縮空氣儲能中的蓄熱技術及其經濟性研究［D］. 北京： 華北電力大學， 2020.

［13］GUO H A， XU Y J， ZHANG Y， et al. Off-design performance and operation strategy of expansion process in compressed air energy systems［J］. International Journal of Energy Research， 2019， 43（1）： 475-490. DOI： 10.1002/er.4284.

［14］CHEN W， BAI J S， WANG G H， et al. First and second law analysis and operational mode optimization of the compression process for an advanced adiabatic compressed air energy storage based on the established comprehensive dynamic model［J］. Energy， 2023， 263： 125882. DOI： 10.1016/j.energy.2022.125882.

［15］SZABLOWSKI L， KRAWCZYK P， BADYDA K， et al. Energy and exergy analysis of adiabatic compressed air energy storage system［J］. Energy， 2017， 138： 12-18. DOI： 10.1016/j.energy.2017.07.055.

［16］XU M J， WANG X， WANG Z H， et al. Preliminary design and performance assessment of compressed supercritical carbon dioxide energy storage system［J］. Applied Thermal Engineering， 2021， 183： 116153. DOI： 10.1016/j.applthermaleng.2020.116153.

［17］GUO H， XU Y J， ZHU Y L， et al. Thermal-mechanical coefficient analysis of adiabatic compressor and expander in compressed air energy storage systems［J］. Energy， 2022， 244： 122993. DOI： 10.1016/j.energy.2021.122993.

［18］CHEN L X， ZHANG L G， YANG H P， et al. Dynamic simulation of a re-compressed adiabatic compressed air energy storage （RA-CAES） system［J］. Energy， 2022， 261： 125351. DOI： 10.1016/j.energy.2022.125351.

［19］WANG S X， ZHANG X L， YANG L W， et al. Experimental study of compressed air energy storage system with thermal energy storage［J］. Energy， 2016， 103： 182-191. DOI： 10.1016/j.energy.2016.02.125.

［20］劉輝. 超臨界壓縮二氧化碳儲能系統熱力學特性與熱經濟性研究［D］. 北京： 華北電力大學， 2017.