基于長記憶性的資產定價模型研究

收稿日期：2024-01-09

基金項目：伊犁州科技計劃項目（YZ2022YD002）；伊犁師范大學校級科研項目（2021YSYB076）

作者簡介：候佳琦（1999-），女，新疆塔城人，在讀碩士，研究方向為數理金融.E-mail：17799378939@qq.com.

*通信作者：王婧（1989-），女，新疆伊寧人，副教授，博士，碩士生導師，研究方向為數理金融.E-mail：wangjing@ylnu.edu.cn.

文章編號：2095-6991（2024）04-0020-09

摘要：建立了基于長記憶性的資產定價模型，考慮做市商通過調節過去的過剩需求比例的決策來出清市場價格，利用離散動力系統的穩定性和分支理論，討論了不動點的存在性以及參數對模型穩定性的影響，重點討論了記憶參數的改變對模型穩定區域的影響，并通過數值模擬得到：當記憶參數在一定區間內變化時，穩定區域會隨著記憶參數的增大而增大，記憶參數的增大會減小股票市場的價格波動.

關鍵詞：長記憶；金融市場模型；穩定區域；數值模擬

中圖分類號：O211.9 """"文獻標志碼：A

Research on Asset Pricing Model Based on Long Memory

HOU Jia-qi1，YANG Zhi1，2，WANG Jing1，2

（1. School of Mathematics and Statistics， Yili Normal University， Yining 835000， Xinjiang， China;

2. Institute of Applied Mathematics， Yili Normal University， Yining 835000， Xinjiang， China）

Abstract：This paper establishes an asset pricing model based on long memory. Considering that the market maker clears the market price by adjusting the decision of the excess demand ratio in the past， the existence of a steady state and the influence of parameters on the stability of the model are discussed by using the stability and branch theory of discrete dynamic systems. The effect of changing the memory parameter on the stability region of the model is focused. Through numerical simulation， the following results are obtained： when the memory parameters change within a certain range， the stable region will increase with the increase of the memory parameters， and the increase of the memory parameters will reduce the price fluctuation of the stock market.

Key words：long memory; financial market model; stable region; numerical simulation

金融資產價格動力學是國內外學者高度關注的課題，指金融市場中資產價格隨時間變化的規律和機制.資產價格動態不僅受政策變化、市場情緒、投資者預期等多種因素的影響，而且對投資者財富具有重大影響.因此，對資產價格動態的分析與預測對于投資者而言至關重要.

在資產價格動態形成過程中，市場出清是一個關鍵的環節，它指的是供求雙方通過交易達到價格平衡的過程.Brock H，Hommes［1-2］ 研究了一種簡單的蛛網模型自適應信念系統，利用局部分岔理論和數值分析的方法，得出異質信念是導致市場不穩定性和奇異吸引子出現的重要因素，并且異質信念也是混沌吸引子的特征.隨后Chiarella和He［3］在此基礎上對模型進行擴展，建立了基于收益和財富比例的離散時間平穩模型，得出資產價格動態模型的本質特征.Chiarella和He［4-5］將風險納入具有異質信念的簡單資產價格模型，得出不同類型投資者的風險厭惡系數會影響資產價格的動態.Hommes［6］研究了由三類投資者組成的自適應進化資產定價動態模型，得出投資者敏感性的提高會使得模型的基本穩態變得不穩定，并且還出現多重穩態.Anufriev M［7］提出了Hommes［6］的資產定價模型的替代版本，該模型具有異質性代理和信念的異步更新，得出適應度并沒有改變基本穩態的穩定性的結論，但是，非基本穩態的穩定性受到了影響.Zhu M［8］研究做市商對金融市場模型穩定性的影響，表明當做市商實現利潤最大化時，并不一定能穩定市場，相反，做市商會受到投機者行為的影響.Sotkiewicz［9］討論了市場出清價格的存在性和非凸性市場經濟分析中整數規劃的強對偶性.Bargigli［10］在Hommes［6］的基礎上引入優化壟斷做市商，表明做市商對市場的穩定性會產生影響.Jungeilges J ［11］將現有的資產異質代理的市場模型進行推廣，考慮了技術分析者和基本面分析者分別在無交易和低交易間隔不一致的情況，結果表明這兩種交易之間的差距程度影響均衡的存在，但不影響其穩定性.

在建立資產價格動態模型中，市場均衡價格的形成機制極為關鍵.做市商出清機制被廣泛應用，如Chiarella和He［3-5］利用做市商價格調整規則pt+1=pt+μze，t來出清市場價格，認為做市商為市場出清價格提供了一種程序化的行為規則.Hommes［6］和Anufriev M［7］采用了同樣的價格調整規則pt+1=pt+μze，t+εt+1，研究了動力系統不動點的穩定性.Day和Huang［14］，Lux［15］，Lux和Marchesi［16-17］以及Farmer和Joshi［18］在金融市場模型中使用了類似的價格調整規則pt+1=pt+cE（pt），其中價格變化基于對過去價格的期望而變化.本文對價格調整規則進行了一個擴展，投資者根據其在前一時期的過剩需求來預測下一時期的價格，重點討論了記憶參數是否會影響原有模型的穩定性，以及記憶參數是否會影響價格的波動.在本文的資產定價設置中，價格調整規則為pt+1=pt+μ［γ（zh，t－zs）+（1－γ）（zh，t－1－zs）］，其優點是：該模型在分析上易于處理，可以通過數值分析得出過去的過剩需求會對未來的價格產生一定的影響.

長記憶性對金融資產價格波動的研究至關重要，并且它與股票價格的跨時間相關性有關.相比傳統定價模型CAPM，長記憶特性能夠更好地捕捉市場的長期依賴和復雜性，從而提高價格預測和風險評估的準確性.基于此，本文建立了基于長記憶性的資產定價模型.

1" 模型建立

參考Anufriev M［7］給出的基礎模型，自適應信念系統為

xt+1=1－μRaσ2+μg2aσ2（1－mt）xt+εt+1，

mt+1=αmt+（1－α）

tanhβ2gaσ2（Rxt2－xt+1xt）－gzsxt－C.（1）

本文考慮市場上兩種類型的投資者：基本面分析者和趨勢追風者.

基本面分析者認為資產價格最終會回到基準價值，這是基于投資者對市場供需關系的分析.盡管市場價格可能會受到各種因素的影響而波動，但長期來看，市場會反應出資產的真實價值.當價格偏離基準價值時，基本面分析者認為存在投資機會，預期價格將會回歸到基準價值.基本面分析者對未來價格期望的預測規則為

E1，tpt+1=p*+vp*－pt，v∈［0，1］，（2）

其中：pt為風險資產的市場價格；p*為基準價值；v為基本面分析者的均值回饋速率.

趨勢追風者與基本面分析者在對市場價格的理解上存在一定的差異.趨勢追風者更側重于短期市場趨勢的捕捉與利用，認為價格會按照當前的趨勢繼續發展，并試圖通過買入漲勢或賣出跌勢來獲取利潤.與基本面分析者相比，趨勢追風者更注重技術分析和市場走勢的判斷，而不是過多關注基本面因素.他們相信市場中存在著明顯的價格趨勢，如上升趨勢、下降趨勢或盤整趨勢，并試圖通過捕捉這些趨勢來進行交易.趨勢追風者對未來價格期望的預測規則為

E2，tpt+1=pt+gpt－pt－1，ggt;0，（3）

其中，g為趨勢參數.

考慮市場價格由做市商出清，在做市商機制下，考慮過去的過剩需求會影響價格，如下：

pt+1=pt+μγze，t+（1－γ）ze，t－1，（4）

其中：μgt;0表示相應的調整速度；γ∈（0，1）為記憶參數，表示過去需求對當前價格的影響程度；ze，t為投資者在t期購買風險資產的總過剩需求.

假設投資者均追求財富效用指數函數最大化，定義超額收益Rt+1=pt+1+yt+1－Rpt，其中R表示無風險資產的總收益，yt+1表示風險資產在t+1時刻支付的隨機紅利.第h類投資者對風險資產的需求zh，t為

zh，t=Eh，tpt+1+yt+1－RptaVh，tpt+1+yt+1－Rpt=

Eh，tpt+1+yt+1－Rptaσ2，（5）

Eh，t，Vh，t分別代表第h類投資者對于超額收益的條件期望和條件方差，a為風險厭惡系數，t時刻的總過剩需求為

ze，t=∑2h=1nh，tzh，t－zs，（6）

其中，zs為外部股票的正供給量.

假設策略異步更新，即在每一期有投資者更新或不更新策略所采用的預測規則.參考Hommes［6］的模型，比例的相應動態由多項式Logit離散選擇模型給出：

nh，t+1=αnh，t+（1－α）eβUh，t－ChZt，

Zt=∑2h=1eβUh，t－Ch，（7）

其中：Ch≥0表示h類投資者每期的平均成本；α表示投資者堅持采用現在策略的比例；Uh，t是適應度函數，即利潤實現值的加權平均值：

Uh，t=pt+1+yt+1－Rptzh，t.（8）

完整的自適應信念系統為

pt+1=pt+μγ（n1，tz1，t+n2，tz2，t－zs）+

（1－γ）（n1，t－1z1，t－1+n2，t－1z2，t－1－zs），（9）

其中，

n1，t+1=αn1，t+（1－α）e［βpt+1+yt+1－Rptz1，t－C1］Zt，

n2，t+1=αn2，t+（1－α）e［βpt+1+yt+1－Rptz2，t－C2］Zt，

z1，t=p*+vp*－pt+y－Rptaσ2，

z2，t=pt+gpt－pt－1+y－Rptaσ2，

Zt=eβpt+1+yt+1－Rptz1，t－C1+

eβpt+1+yt+1－Rptz2，t－C2.

為了方便計算，假設噪聲項εt+1=yt+1－y是獨立同分布的，并且采用基本價格偏離值xt=pt－p*.通過計算，自適應信念系統被更新為

xt+1=Axt+Bxt－1，mt+1=αmt+（1－α）tanhβ2（D－C），yt+1=xt，ht+1=mt.（10）

其中，

A=1+

μγ2（1－R+g）－（1+v+g）（1+mt）2aσ2，

B=

μ（1－γ）2（1－R+g）－（1+v+g）（1+mt－1）2aσ2，

D=

－xt（1+v+g）（xt+1－Rxt+yt+1－y+aσ2zs）aσ2.

本文考慮沒有噪聲項εt+1=yt+1－y的情況，即εt+1=0.C=C1－C2lt;0表示基本面分析者的每一期信息收集成本低于趨勢追風者.下面通過考慮外部股票的正供給zs=0的情況來研究記憶參數γ對自適應信念系統的影響.

2" 動力系統的討論

在這一節中，研究0≤αlt;1時系統的局部穩定性和分支情況，排除了α=1的情況，若α=1，則表示投資者從來不更新他們的信念.

定理1" 動力系統（10）存在不動點E=0，tanh－βC2，0，tanh－βC2.

定理2" （1）若0lt;γ≤3/4，0lt;μlt;μ1，其中μ1=2aσ2/{（1－γ）［（1+m）（g+v+1）－2（1－R+g）］}，則不動點E是局部漸近穩定的.當μ=μ1時，E會產生周期加倍分支；當μgt;μ1，E為鞍點.

（2）若3/4lt;γlt;1，0lt;μlt;μ2，其中μ2=4aσ2/{（2γ－1）［（1+m）（g+v+1）－2（1－R+g）］}，則不動點E是局部漸近穩定的.當μ=μ2，E會產生周期加倍分支；當μgt;μ2，E為鞍點.

定理2說明，不動點E的穩定性區域是基于做市商的調整速度以及基本面分析者的均值回饋速率.當記憶強度較弱時，即0lt;γ≤3/4，μlt;μ1時，穩定區域通常能夠保持穩定，當參數μ達到μ1的臨界值時，不動點E會經歷一個周期加倍的分支，標志著系統的周期性行為發生變化.進一步，當μ超過μ1后，不動點E轉變為鞍點，表明在這個參數值下，不動點的穩定性喪失，系統朝更復雜或不規則的狀態發展.

定理3" 不動點E的局部漸近穩定區域為

D（γ，a，σ）=（γ，a，σ）：0lt;γ≤3/4，

agt;a1，或3/4lt;γlt;1，agt;a2.

其中：a1=μ（1－γ）（m+1）（v+g+1）－2（1－R+g）/（2σ2）;a2=

μ（2γ－1）（m+1）（v+g+1）－2（1－R+g）/（4σ2）.

定理3說明，不動點E的穩定性受到風險厭惡系數以及投資者對超額收益條件方差的預期影響.在記憶強度較低的情況下，即0lt;γ≤3/4，agt;a1時，不動點E的穩定性區域往往能夠維持其穩定性.而在記憶強度較高的區間，即3/4lt;γlt;1，agt;a2時，穩定區域通常能夠保持穩定.

證明" 為了討論方便，假設yt+1=xt，ht+1=mt，構造映射

F：（xt+1，mt+1，yt+1，ht+1）→（x1，m1，y1，h1）.

式（10）變為

x1=A1x+B1y，m1=αm+（1－α）tanhβ2（D1－C），y1=x，h1=m.（11）

其中

A1=1+μγ［2（1-R+g）-（1+v+g）（1+m）］/（2aσ2），

B1=μ（1－γ）［2（1－R+g）－（1+v+g）（1+m）］/（2aσ2），

D1=－xt（1+v+g）（1－R）x2aσ2.

模型（11）在不動點E處的雅可比矩陣為

J=A10B10m1xαm1y010000100，

其對應的特征方程（λ為特征根）：λ（λ－α）Γ（λ）=0，Γ（λ）=λ2－A1λ－B1.由于0≤αlt;1，所以只考慮Γ（λ）的兩個特征根是否在單位圓內，參考周義倉［19］所給出的Schur-Cohn判據可得

Γ（1）=1－A1－B1gt;0，（－1）2Γ（－1）=1+A1－B1gt;0，1+B1gt;0，1－B1gt;0.

通過求解定理2、定理3得證.

3" 數值分析

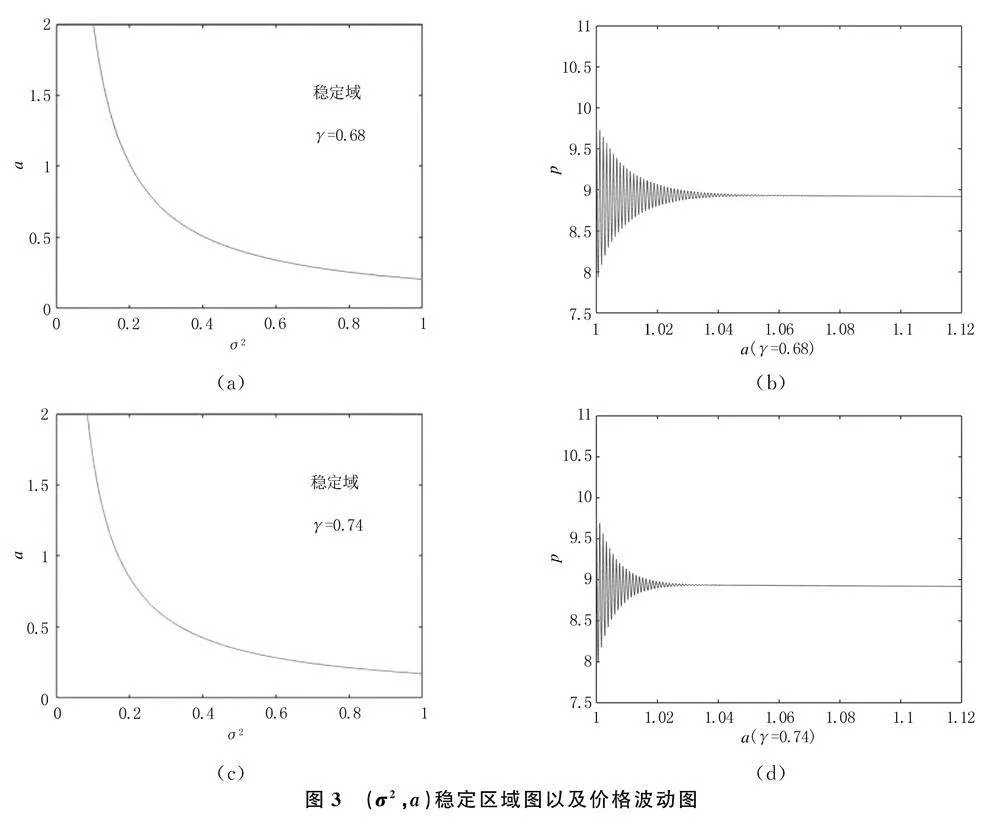
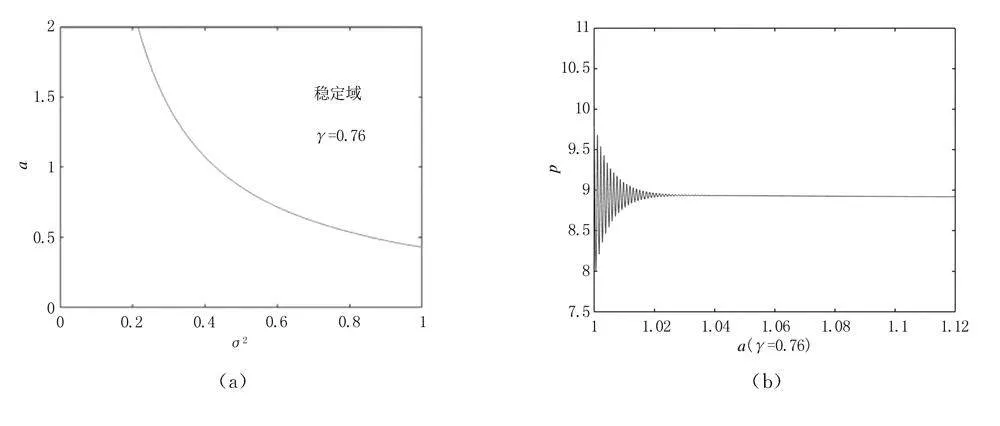
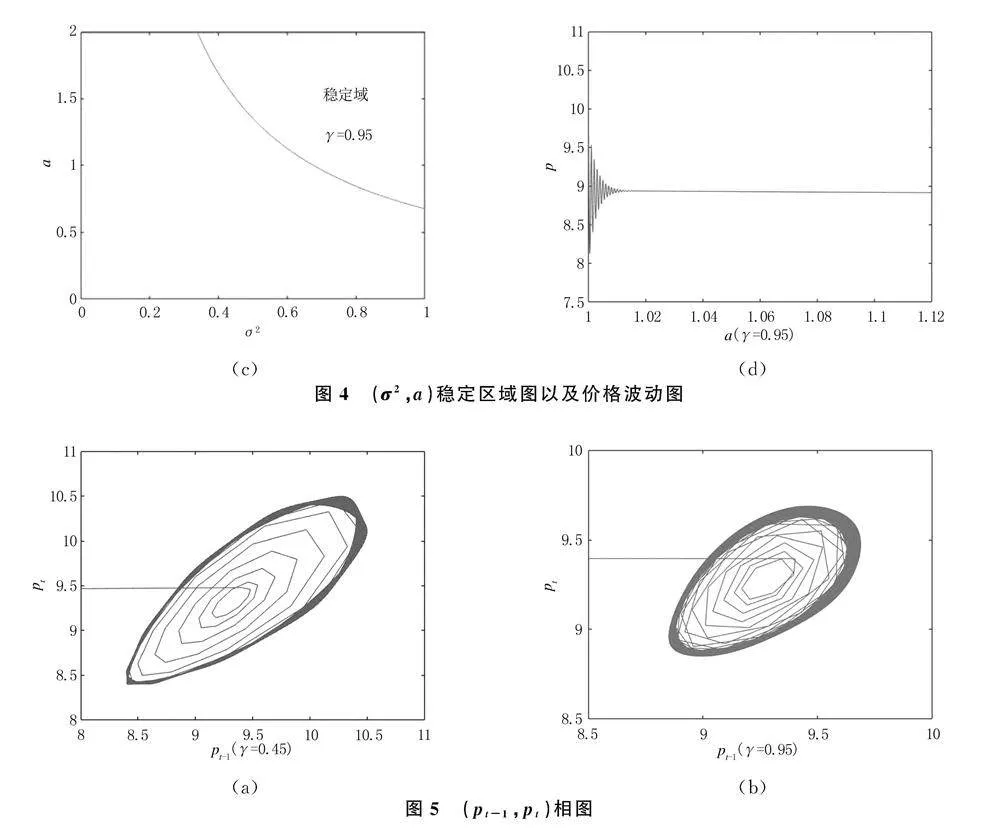
選取參數α=0.5，C=1，R=1.1，g=1.16，考慮記憶參數γ對模型（10）的影響.基于定理2，利用MATLAB軟件繪制出（v，μ）所確定的穩定區域，以及隨著μ變化的價格波動圖，如圖1，圖2所示.同樣，基于定理3，繪制出（σ2，α）所確定的穩定區域，以及隨著α變化的價格波動圖，如圖3，圖4所示.

圖1表明：當γlt;0.75的情況下，隨著記憶參數γ的增大，不動點的穩定區域在不斷變大，這意味著市場的穩定性有所提升.具體而言，當γ=0.25時，μ大概在1.57處開始出現波動；當γ=0.55時，μ大概在1.62處開始出現波動.由此說明，當γlt;0.75的情況下，記憶參數γ的增大可以減小股票市場價格的波動.當記憶參數γ較小，即1－γ較大時，根據公式（9）表明投資者對過去價格的變動和趨勢的關注度增高，更傾向于根據過去信息和最新數據進行決策，這有助于市場價格的穩定.這意味著投資者能夠通過對過去需求變動的分析來制定投資策略，而不是盲目追隨短期趨勢.在這種情況下，市場參與者的決策可能更加穩健和理性，從而降低市場波動的風險.

圖2表明：當γgt;0.75的情況下，隨著γ的增大，不動點的穩定區域逐步收縮，這意味著市場的穩定性也在減小.當γ=0.85時，μ大概在1.74處開始出現波動；當γ=0.95時，μ大概在1.63處開始出現波動.由此說明當γgt;0.75的情況下，記憶參數γ的減小可以減小股票市場價格的波動.當記憶參數γ較大，即1－γ較小時，根據公式（9）表明市場投資者對過去價格變動和趨勢的重視程度下降，更傾向于根據現在信息和最新數據進行決策.這種策略會導致投資者對短期市場變動的響應更加靈敏，而非過度依賴歷史數據.因此，市場的價格決策可能表現出更高的即時性，與此同時，對長期趨勢的忽視可能會增加市場的波動性.

圖3表明：當γlt;0.75的情況下，隨著記憶參數γ的增大，不動點的穩定區域在不斷變大，這意味著市場的穩定性也在增加.當γ=0.68時，a在1.05處開始變得平穩；當γ=0.74時，a在1.03處開始變得平穩，說明當γlt;0.75的情況下，記憶參數γ的增大可以減小股票市場價格的波動.這說明在較大的風險厭惡系數下，即投資者對風險的厭惡程度較高，投資者更傾向于選擇穩定回報的投資，而不愿意承擔過大的風險.當市場風險增大時，投資者的這種行為傾向會更加突出，會更積極地尋求穩定性和安全性，從而有助于市場的穩定.因此，風險厭惡系數的大小在一定程度上影響了市場的穩定性和波動性.

圖4表明：當γgt;0.75時，隨著記憶參數γ的增大，不動點的穩定區域在不斷變小，這意味著市場的穩定性也在減小.當γ=0.76時，a在1.03處開始變得平穩；當γ=0.95時，a在1.01處開始變得平穩，說明當γgt;0.75的情況下，記憶參數γ的減小可以減小股票市場價格的波動.

為了更好地理解價格的波動過程，并能清晰地觀察價格在不同時間點之間的關聯性和演變趨勢，采用相圖的方式來呈現，如圖5所示.

通過對相圖的分析，可以得出以下結論：在參數值達到邊界點時，股票市場中出現了極限環現象，其中價格圍繞一定的范圍波動.當參數接近邊界點時，不動點的穩定區域變得非常小，同時市場價格在一個有限的范圍內反復波動，形成了極限環.極限環的存在表明股票市場在邊界點附近具有一定的自適應性和非線性特征.市場價格在極限環內波動，是因為投資者對于價格的預期和行為會受到邊界條件的制約，導致價格在某個特定范圍內波動.

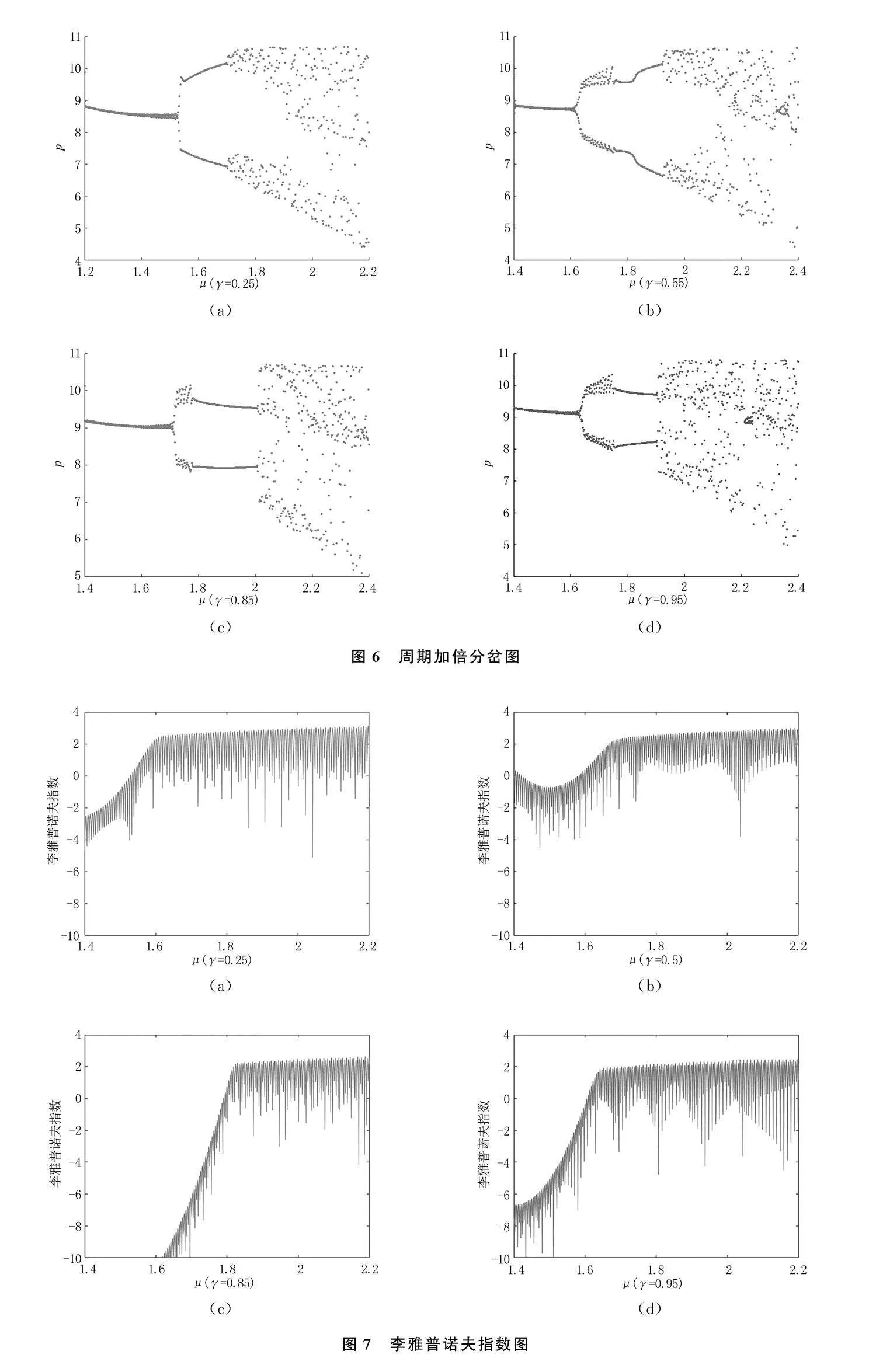
根據定理2可以知道當μ=μ1或者μ=μ2

時系統會出現周期加倍分岔現象，從而導致系統的穩定性發生變化.為了更好地觀察和分析這種現象，制作了周期加倍分岔圖，如圖6所示.

圖6表明：從周期加倍分岔圖中發現出現了周期加倍點，即當參數變化到一定程度時，系統的運動周期被加倍，之后又進一步分叉，形成更加復雜的運動模式.分岔點處的運動周期成倍遞增.從

圖6（a）可以看出分岔點大概在μ=1.57以及μ=1.68處，從圖6（b）可以看出分岔點大概在μ=1.62以及μ=1.91處，說明當γlt;0.75的情況下，隨著記憶參數γ的增大，分岔點在不斷地變大，說明穩定區域也在不斷的變大；從圖6（c）可以看出分岔點在μ=1.74以及μ=2.1處，從圖6（d）可以看出分岔點在μ=1.63以及μ=1.93處，說明當γgt;0.75的情況下，隨著記憶參數γ的增大，分岔點在不斷的變小，說明穩定區域也在不斷的變小.

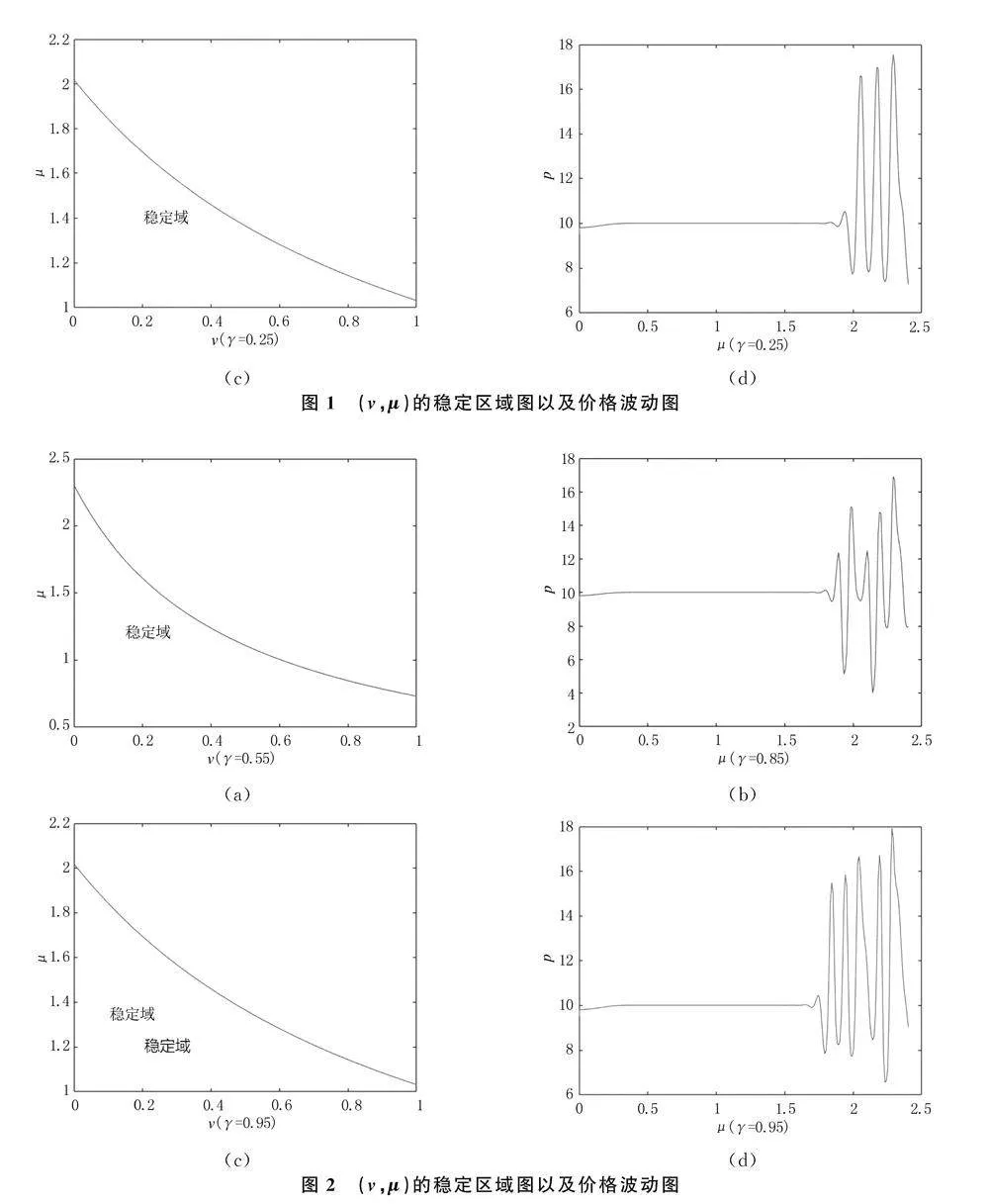
為了更好地理解系統的穩定性和混沌性質，根據系統（10）繪制出的李雅普諾夫指數圖，如圖7所示.這個圖可以用來測量系統狀態的敏感程度和預測其未來行為.

李雅普諾夫指數可以用來衡量系統的混沌程度.具體來說，當李雅普諾夫指數都是負數時，系統表現為穩定狀態；當存在正的李雅普諾夫指數時，系統即呈現混沌.從圖7（a）可以看出μ=1.57

時系統開始發生混沌，從圖7（b）可以看出μ=1.62時系統開始發生混沌，這表明，當γlt;0.75的情況下，伴隨著記憶參數γ的增大系統的穩定區域在不斷增大；從圖7（c）可以看出μ=1.74時系統開始發生混沌，圖7（d）可以看出μ

=1.63時系統開始發生混沌，說明當γgt;0.75時，隨著記憶參數γ的增大，系統的穩定區域在不斷變小.

綜上，當γlt;0.75時，通過穩定區域圖分析可以看出，隨著記憶參數γ的增大，穩定區域逐漸擴大；進一步的，股票市場價格波動圖顯示：隨著記憶參數γ的增大，價格的波動逐漸減弱.同時，對周期加倍分岔圖和李雅普諾夫指數圖的聯合觀察表明，隨著記憶參數γ的增大導致分岔點在不斷變大，混沌現象出現的閾值也相應提高，進一步驗證了穩定區域隨記憶參數提升而擴大的結論.相反，γgt;0.75的情況下，穩定區域隨著記憶參數γ的增加而減少；股票市場價格波動圖則顯示，價格波動隨記憶參數γ的降低而減少；從周期加倍分岔和李雅普諾夫指數圖對比可以觀察

到，記憶參數γ的增大使得分岔點提前出現，李雅普諾夫指數表征的混沌開始點也隨之前移，從而說明穩定區域隨記憶參數的降低而變大.

4" 結語

本文主要研究了一種具有長記憶性的資產定價模型.考慮了投資者在決策過程中對過去需求波動的認知與反應，從而揭示了市場價格變動所表現出的一定程度的慣性或長期相關性.這種現象在經濟學領域被稱為“長期記憶效應”，對金融市場的穩定性和預測準確性具有深遠影響.通過運用離散動力系統的穩定性、分支理論以及數值分析等方法，研究了長記憶性資產定價模型的內在機制，以及市場價格波動與投資者行為之間的關系.在研究中得到結論：記憶參數在特定區間的增加會減小市場價格波動.該結論表明，當投資者的交易行為對過去需求波動的記憶和反應程度減弱時，市場價格的波動幅度會相應降低，從而提高金融市場的穩定性.

參考文獻：

［1］ BROCK W A，HOMMES C H.A rational route to randomness［J］.Econometrica，1997，65（4）：1059-1095.

［2］ BROCK W A，HOMMES C H.Heterogeneous beliefs and routes to chaos in a simple asset pricing model［J］.Journal of Economic Dynamics and Control，1998，22（8）：1235-1274.

［3］ CHIARELLA C，HE X.Asset price and wealth dynamics under heterogeneous expectations ［J］.Quantitative Finance，2001，1 （5）：509.

［4］ CHIARELLA C，HE X.Heterogeneous beliefs，risk and learning in a simple asset pricing model ［J］.Computational Economics，2002，19（1）：95-132．

［5］ CHIARELLA C，HE X.Heterogeneous beliefs，risk and learning in a simple asset pricing model witll a market maker ［J］.Macroeconomic Dynamics，2003，7（4）：503-536.

［6］ HOMMES C，HUANG H，WANG D.A robust rational route to randomness in a simple asset pricing model ［J］.Journal of Economic Dynamics and Control，2005，29（6）：1043-1072.

［7］ ANUFRIEV M，TICHY T，LAMANTIA F，et al.An asset pricing model with accuracy-driven evolution of heterogeneous expectations ［J］.Communications in Nonlinear Science and Numerical Simulation，2023，117（Sup C）：106975.

［8］ ZHU M，CHIARELLA C，HE X Z，et al.Does the market maker stabilize the market？ ［J］.Physica A：Statistical Mechanics and its Applications，2009，388（15-16）：3164-3180.

［9］ O’NEILL R，SOTKIEWICZ P，HOBBS B，et al.Efficient market-clearing prices in markets with nonconvexities ［J］.European Journal of Operational Research，2005，164（1）：269-285.

［10］ BARGIGLI L.A model of market making with heterogeneous speculators［J］.Journal of Economic Interaction and Coordination，2020，16（1）：1-28.

［11］ JUNGEILGES J，MAKLAKOVA E，PEREVALOVA T.Asset price dynamics in a “bull and bear market”［J］.Structural Change and Economic Dynamics，2021，56（Sup1）：117-128.

［12］ HRTEL P，KORPARING S M.Demystifying market clearing and price setting effects in low-carbon energy systems［J］.Energy Economics，2021，93：105051.

［13］ CHEN H，FU L，BAI L，et al.Distribution market-clearing and pricing considering coordination of DSOs and ISO：An EPEC approach［J］.IEEE Transactions on Smart Grid，2021，12（4）：3150-3162.

［14］ DAY R H，HUANG W.Bulls，bears and market sheep［J］.Journal of Economic Behavior amp; Organization，1990，14（3）：299-329.

［15］ LUX T.Herd behaviour，bubbles and crashes［J］.The Economic Journal，1995，105（431）：881-896.

［16］ LUX T，MARCHESI M.Scaling and criticality in a stochastic multi-agent model of a financial market［J］.Nature，1999，397（6719）：498-500.

［17］ LUX T，MARCHESI M.Volatility clustering in financial markets：a microsimulation of interacting agents［J］.International Journal of Theoretical and Applied Finance，2000，3（4）：675-702.

［18］ FARMER J D，JOSHI S.The price dynamics of common trading strategies［J］.Journal of Economic Behavior amp; Organization，2002，49（2）：149-171.

［19］ 周義倉，曹慧，肖燕妮.差分方程及其應用［M］.北京：科學出版社，2014：134-135.

［責任編輯：趙慧霞］