基于自適應虛擬阻抗的構網型與跟網型逆變器主導微網系統無功功率均分控制策略

邱曉燕,閆幸,周毅,林號縉,臧天磊,周步祥

(四川大學電氣工程學院,成都市 610065)

0 引 言

隨著風、光等可再生能源在電網中的大量接入,微網系統作為連接分布式發電單元(distributed generation,DG)、存儲設備和負載的分布式電網,具備整合大規模可再生能源并以孤島模式保持負載電力需求的能力,是發展“低碳”能源系統的重要組成部分。為防止DG過載與電壓偏移較大,微網分層控制中要求頻率與電壓趨于額定值以及功率按照容量比例分配。然而,由于逆變器電源控制方式不同、容量不等、輸電線路阻抗不匹配、下垂系數設置不合理等,導致無功功率難以實現均分[1-3]。其中,逆變器間的線路阻抗不匹配會造成微網中的負荷功率分配不均,從而引發環流現象[4-5],環流的存在不僅會影響負荷的均分,降低功率傳輸效率,還會造成系統中大量電力電子設備過熱損耗,縮短設備壽命使其安全性能降低[6-7]。基于逆變器容量反比設置下垂系數實現無功功率均分可減少環流[8-9],不同逆變器根據自身容量比例提供無功功率可防止單個逆變器電源過載[9-10]。因此基于逆變器容量實現無功功率均分具有重要意義。

針對上述問題,現有方法主要包括虛擬阻抗法、電壓狀態觀測器法、分布式一致性算法等。虛擬阻抗法一般應用于并聯構網型(grid-forming,GFM)逆變器間,基于阻抗估計與環流[8,11]、偏差信息[12-14]等驅動生成虛擬阻抗項,使補償后等效線路阻抗相等[15-16],或使線路阻抗特性滿足下垂控制條件[17-19],最終實現無功功率均分。電壓狀態觀測器法基于GFM逆變器間信息交換估計母線平均電壓[20],可權衡實現電壓恢復與無功功率均分。分布式一致性算法基于GFM逆變器電壓與無功功率偏差生成調節項補償至下垂控制環節[21],后續研究一般在此基礎上計及額外約束[22-24]實現無功功率均分與電壓恢復。上述方法中二次調節項一般補償至GFM逆變器的電壓環或下垂環節,或通過調節平均電壓實現功率均分,因此難以直接應用于跟網型(grid-following,GFL)逆變器參與二次功率分配的情形[25]。

微網系統在大規模負載擾動下,僅GFM逆變器參與二次功率分配可能因調節能力不足出現電壓偏移較大與過載[10]。此外,微網與分布式電源標準IEEE 1547也推薦GFL逆變器利用最大功率點剩余容量參與二次功率控制充分發揮調節潛力,通過注入無功改善電壓分布[26],因此考慮GFL逆變器參與功率的二次調節具有積極意義。

基于傳統控制策略的GFM與GFL逆變器由于控制方式不同難以直接實現二次功率調節的統一控制。為此,部分文獻提出了應對策略:文獻[27]提出在GFL和GFM逆變器控制中增加二次調節項,分別通過頻率與電壓偏差調節有功與無功功率,確保逆變器間功率精確分配,但其未驗證即插即用與逆變器容量不等情況下所提策略的適用性。文獻[28]針對孤島微網基于電壓方差調節提出了一種實現平均電壓恢復和無功功率分配的分布式控制方案。然而,由于其控制目標需施加在某個DG上,由此產生的特殊性可能導致其與未施加控制目標的DG無功功率分配結果偏差較大[29]。文獻[30]提出了一種考慮GFL與GFM逆變器的孤島微網統一建模方法,基于功率解耦與擴展狀態觀測器(extended state observer,ESO)將不同逆變器內部動態特性與控制結構統一,最終實現電壓收斂于額定值且無功功率均分;但電壓觀測器類方法可能因引入初值問題導致無功功率難以收斂至均分值。

另一方面,上述方法對于特定場景的適用性尚待驗證[27],或依賴于過程較為復雜的非線性控制[29-30]。因此,文獻[9]提出將倒下垂控制應用于GFL逆變器,使其具備類似GFM逆變器的功率下垂調節能力,從而可基于文獻[21]中GFM逆變器控制策略得出全逆變器微網系統中完全協調控制GFM與GFL逆變器的主從一致性二次控制方案,實現頻率/電壓恢復、功率均分并抑制無功功率環流,適用于即插即用與通信退化等情形;文獻[10]基于GFL逆變器倒下垂控制提出了虛擬阻抗策略用以解決因GFM與GFL逆變器間線路阻抗不匹配導致的無功功率分配問題。然而,文獻[9]中主從控制方式下對主節點逆變器性能可靠性要求更高,文獻[10]所提常值虛擬阻抗需預知阻抗值且無法適應線路阻抗的變化。

為解決上述問題,本文將倒下垂控制應用于GFL逆變器使其具備類似GFM逆變器的功率下垂特性;在此基礎上,通過相鄰逆變器無功功率偏差驅動GFM與GFL逆變器中虛擬阻抗控制環路自適應補償異構逆變器間偏差信息,實現GFL逆變器對微網系統無功功率的主動支撐,從而使GFM與GFL逆變器間無功功率均分并實現電壓恢復,增加微網的無功功率調節能力。本文的主要創新點在于:通過倒下垂控制使GFL逆變器主動參與功率的二次調節,對微網系統采用可靠性較高的對等控制,由相鄰GFL與GFM逆變器無功功率偏差驅動自適應調節虛擬阻抗實現無功功率均分與電壓恢復。

1 構網型與跟網型變流器主導的孤島微網系統簡介

本文研究的GFM與GFL逆變器主導的孤島微網示意如圖1所示,分布式逆變器電源通過聯絡線接入公共連接點(point of common coupling,PCC)共同向負載供電。其中DG1采用的構網控制方式為下垂控制,輸出特性表現為受控電壓源,DG2采用的跟網控制方式為倒下垂控制,輸出特性表現為受控電流源[31]。

圖1 GFM與GFL逆變器主導的微網系統示意Fig.1 Microgrid system dominated by GFM and GFL inverters

圖1中,負荷1為6 000 W+6 000 var,其他電路參數如表1所示。

表1 GFM與GFL逆變器主導微網電路參數Table 1 Parameters of microgrid system dominated by GFM and GFL inverters

1.1 基于下垂控制的GFM逆變器

GFM逆變器下垂控制包括有功-頻率與無功-電壓控制[32-33],可表示為:

ω1=ωref-m1P1

(1)

V1=Vref-n1Q1

(2)

式中:ω1為角頻率;V1為電壓幅值;ωref和Vref分別為角頻率與電壓幅值的參考值;m1和n1分別為GFM逆變器頻率-有功、電壓-無功下垂系數;P1與Q1為輸出功率。

GFM逆變器電壓角度、角頻率與頻率關系為:

(3)

式中:φ1為電壓角度;f為頻率。

式(1)—(3)可實現GFM逆變器的基本控制。整體控制框圖[9]如圖2所示,含*變量為未濾波值。其中一階低通濾波器可表示為:

(4)

式中:L(s)為一階低通濾波器傳遞函數;ωf為截止頻率。

1.2 基于倒下垂控制的GFL逆變器

GFL逆變器基本控制中的同步坐標系鎖相環(SRF-PLL)可表示為:

(5)

式中:θ為GFL逆變器的鎖相角;ω2為對微網q軸電壓鎖相得到的角頻率;kppll與kipll分別為PI控制的比例和積分系數;vq2為輸出側q軸實時電壓值;s為拉普拉斯算子。

借鑒同步發電機組的一次調節原理參照GFM逆變器引入倒下垂控制。倒下垂控制與dq軸參考電流可表示為:

(6)

(7)

(8)

(9)

綜上,基于倒下垂控制的GFL逆變器控制框圖[9]如圖3所示。與前述1.1節相比,GFM逆變器通過測量輸出功率并發送頻率和電壓參考信號,而GFL逆變器與之相反,兩者表現出對偶特性[34]。

圖3 GFL逆變器控制框圖Fig.3 Control block diagram of GFL inverter

2 線路阻抗與無功下垂系數對無功功率分配的影響

對于圖1所示GFM與GFL逆變器主導微網系統,以功率容量相等為例,無功-電壓下垂系數相等時,實現無功功率均分需GFL與GFM逆變器滿足下式:

Im[V1∠φ1·(I1∠δ1)*]=Im[V2∠φ2·(I2∠δ2)*]

(10)

式中:Vi為逆變器輸出電壓有效值,i=1,2;Ii為輸出電流有效值,i=1,2;φi與δi分別為輸出電壓與輸出電流與公共連接點間夾角,i=1,2。

當線路阻抗不匹配時,無功分配情況可描述如下:

(11)

式中:VPCC為公共點電壓有效值;Xi為線路感抗;Vref為電壓參考值;ni為無功-電壓(倒)下垂系數。因VPCC和Vref遠大于Xi,線路阻抗不匹配加重了微網無功功率分配不均的效果,甚至可能會導致系統失穩[35]。

實際運行中,由于各逆變器電源到母線處的線路阻抗不相等,導致式(10)難以滿足,使得逆變器間無法按照容量比實現無功功率均分。此時調節無功下垂系數可改善無功功率分配,如圖4所示,其中下標1為GFM逆變器,下標2為GFL逆變器。當n>n′時,ΔQ′>ΔQ,ΔV>ΔV′,表明下垂系數越大無功功率越趨于均分,但電壓越偏離額定值,且過大的下垂系數會惡化系統穩定性[35],因此精確的無功功率均分需另尋控制策略實現。

圖4 調節無功下垂系數改善無功功率分配Fig.4 Adjust reactive parameter to regulate reactive power sharing

3 基于自適應虛擬阻抗的跟網型與構網型逆變器無功均分策略

3.1 虛擬阻抗控制原理

針對逆變器并聯時線路阻抗不匹配導致的輸出側電壓與無功分配偏差問題,可通過虛擬阻抗法[17]解決。其原理如圖5(a)所示:設GFM逆變器(DG1)與GFL逆變器(DG2)容量相等,線路阻抗Zl2>Zl1,A點與B點因阻抗不匹配導致無功分配不均,通過對線路2引入虛擬阻抗Z*使B*處電壓與A處接近以補償因阻抗不匹配產生電壓降同時抑制環流,最終實現無功功率均分。其控制過程如圖5(b)所示。

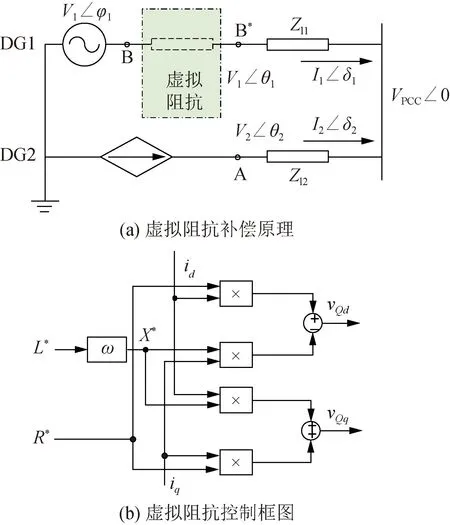
圖5 虛擬阻抗控制原理Fig.5 Principle of virtual impedance control

3.2 適用于GFL與GFM逆變器主導微網系統的自適應虛擬阻抗控制策略

由于實際微網中線路阻抗難以測量且一般不相等,補償常值虛擬阻抗已不再適用,因此考慮基于分布式一致性自適應調節[36]無功功率偏差的自適應虛擬阻抗策略。

廣義上的無功功率均分可表示為:

niQi=njQj

(12)

式中:ni/j為電壓-無功(倒)下垂系數;Qi/j為逆變器輸出無功功率。每個DG的無功功率控制器在比較本地與鄰近逆變器無功后生成無功功率偏差:

(13)

式中:aij為反映鄰接矩陣中通信鏈路連通變化條件的元素,相連為1,否則為0;Ni為可與第i個逆變器通信的逆變器集合。

(14)

式中:δQi為基于相鄰逆變器無功偏差經積分生成的補償量;kQi為無功偏差積分系數。所提出的自適應虛擬阻抗控制如圖6所示。

圖6 自適應虛擬阻抗控制框圖Fig.6 Control block diagram of adaptive virtual impedance

虛擬阻抗環節最終生成的電壓矯正項如式(15)所示,補償至GFM逆變器的一次電壓環與GFL逆變器的倒下垂無功-電壓控制環節。

(15)

式中:vgd與vgq為通過虛擬阻抗生成的電壓矯正項;id與iq為逆變器輸出電流的dq軸分量。

由于GFM逆變器需提供電壓幅值支撐,故基于式(2)增加電壓恢復控制:

(16)

式中:v為電壓恢復項;kv為電壓恢復項積分系數。

3.3 無功偏差積分系數對無功功率收斂過程的影響

上述虛擬阻抗控制中,無功偏差積分系數kQi會影響無功功率的收斂特性,需在一定范圍內選取以權衡系統阻尼與響應速率。因此本部分重點分析kQi對逆變器系統無功功率收斂過程的影響。

以GFM與GFL逆變器各1臺為例,自適應虛擬阻抗產生的虛擬電感值可表示為:

(17)

式中:Lvir為虛擬電感。

對本地逆變器而言,相鄰逆變器經通信輸送的無功信息可視為參考值,此時式(17)的小信號模型為:

(18)

虛擬電感等效補償至線路阻抗處,如圖5(a)所示,此時無功功率可表示為:

(19)

式中:VB、VB*分別為圖5(a)中DG1虛擬阻抗兩端電壓幅值;θ為電壓相角;φ為電流相角;ω為角頻率。

忽略電流電壓環等動態過程,式(19)的小信號模型為:

(20)

式中:Q20、Lvir0為無功功率與虛擬電感穩態值。計及無功-電壓下垂(倒下垂)控制中的一階低通濾波器,聯立式(18)—(20)可得系統簡化傳遞框圖,如圖7所示。

圖7 系統簡化傳遞框圖Fig.7 Simplified transform block diagram of system

圖7對應的傳遞函數為:

(21)

對于式(21)所示二階系統,其阻尼系數與自然振蕩頻率可表示為:

(22)

式中:ωn與ζ分別為系統自然振蕩頻率與阻尼系數。

由式(22)可得:ωn隨kQ2增大而增大,此時系統響應速率增加,但阻尼系數ζ變小,響應速率與阻尼系數變化趨勢相反,因此實際運行中應兼顧兩者折中取值,對于具體微網系統該系數的選取方法詳見4.1節。

4 仿真驗證

為了驗證本文所提出的自適應虛擬阻抗策略可行性,在MATLAB/Simulink中搭建含GFM與GFL逆變器各1臺的微網系統仿真模型,其中DG1為GFM逆變器,DG2為GFL逆變器,如無說明則逆變器容量比均為1。系統仿真參數如表2所示,仿真案例如表3所示。負荷2參數為6 000 W +3 000 var,后續負荷3參數為3 000 W+6 000 var。

4.1 無功偏差積分系數選取方法

為保證后續案例中無功輸出穩定且響應速率良好,需先確定無功偏差積分系數kQi的取值范圍并選取合適值[37-38]。圖8為5種不同kQi值下對應的無功功率曲線收斂過程,當kQi=0.003 5時曲線模態為過阻尼,無功功率在3 s左右穩定;隨著kQi逐漸增大至0.020 0,無功功率曲線逐步過渡至欠阻尼模態,輸出曲線在2.5 s左右趨于穩定。

圖8 不同kQi下無功功率收斂過程Fig.8 Reactive power convergence process of different kQi

隨著kQi的增大,系統響應速率增加但阻尼隨之下降,此時系統穩定性變差。因此綜合考慮kQi取值區間為[0.002,0.100],后續案例研究中如無說明均取kQi為0.005。

4.2 案例1:對比未采用自適應虛擬阻抗

為直觀且準確比較采用本文提出的自適應虛擬阻抗控制策略前后對于GFL與GFM逆變器間無功功率均分與電壓恢復效果,定義無功功率偏差率nQ與電壓偏差率nV如下所示:

(23)

(24)

式中:N為DG數量,偏差率越小表明無功功率均分效果越好,平均電壓越接近于標幺值。

設定2臺逆變器容量為1∶1,僅線路阻抗不等,具體參數如表1所示。此時僅接入負荷1。

圖9 未采用與采用自適應虛擬阻抗仿真結果Fig.9 Simulative waveforms of proposed strategy without and with application

對圖9所得結果分析如下:

1)從圖9(a)可以看出,在1.5 s前由于線路阻抗不匹配導致逆變器存在無功功率偏差,DG1與DG2分別為2 843 var與3 027 var,偏差率為3.23%;2.0 s后完全采用所提策略,穩定時DG1與DG2無功功率分別為2 869 var與2 868 var,此時偏差率為0.18%,相比于采用所提策略前明顯減小。

2)從圖9(b)可以看出,有功功率不受線路阻抗影響,在2.0 s完全采用所提策略后穩態時DG1與DG2有功功率相等。

3)從圖9(c)可以看出,在2.0 s完全采用所提策略后,GFL逆變器電壓由0.986 pu恢復至0.995 pu,GFM逆變器電壓則由0.995 pu恢復至標幺值。相比于采取所提策略前,電壓偏差率由1.15%降低至0.25%。

分別改變DG1與DG2線路電感為4 mH與1 mH,仿真結果如圖10所示。從圖10(a)可以看出,隨著線路電感不匹配度加重,采用所提策略前后無功偏差率分別為13.15%與1.14%;從圖10(b)可以看出,有功功率最終實現均分;從圖10(c)可以看出,此時GFM與GFL逆變器電壓分別由0.991 pu與0.986 pu恢復至1.00 pu與0.990 pu,電壓偏差率相應由1.1%降低至0.5%。與文獻[10]中采用的常值虛擬阻抗法相比,本文所提策略無需預知阻抗值,可自適應線路阻抗變化實現功率均分與電壓恢復。

圖10 線路電感變化后輸出無功與電壓Fig.10 Reactive power and voltage with line inductance changing

從圖9(d)可以看出,DG2與DG1的自適應虛擬電感在2.5 s趨于穩態值±1 mH;從圖10(d)可以看出,DG2與DG1虛擬電感穩態值為±2.15 mH,補償后等效線路電感并不相等。其原因在于GFL逆變器電壓僅基于GFM逆變器電壓支撐而未受控,因此其穩態值與GFM逆變器輸出電壓穩態值存在偏差,使得補償后電感不等但仍可實現無功分配。由于圖10對應場景下線路電感偏差較圖9增加,因此DG1與DG2輸出電壓偏差與等效線路阻抗偏差亦增加。

上述兩種情形下負荷節點(VPCC)電壓幅值如圖11所示。從圖11(a)可以看出,未采用所提策略前負荷節點電壓為0.950 pu,t=2.0 s采用所提策略后隨著逆變器輸出電壓幅值恢復至標幺值,負荷節點電壓亦恢復至0.960 pu;從圖10(b)可以看出,未采用所提策略前負荷節點電壓為0.960 pu,t=2.0 s采用所提策略后恢復至0.965 pu,因此逆變器輸出側電壓幅值的恢復亦有利于負荷節點電壓幅值的改善。

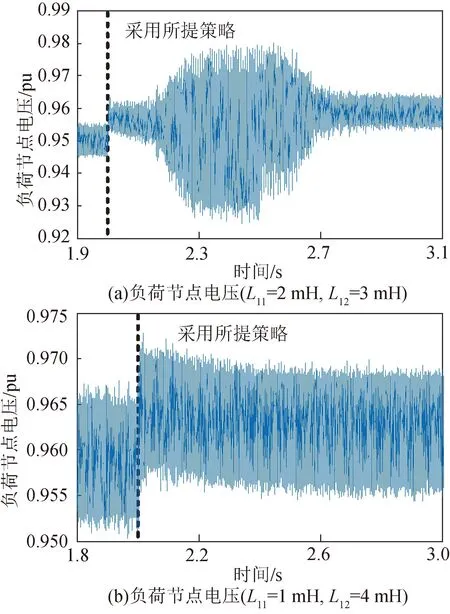
圖11 案例1未采用與采用所提策略時VPCC波形Fig.11 Load voltage amplitude of Case1 without and with proposed strategy

由于所提策略主要通過控制逆變器輸出端電壓實現幅值恢復而并未對負荷側電壓進行控制,故負荷節點電壓未恢復到標幺值附近,但仍然在供電電壓偏差所規定的標稱值±7%(0.93～1.07 pu)范圍內。

設定GFM與GFL逆變器容量比為2∶1且令GFL逆變器倒下垂系數增加一倍,其余參數同表1與表2,此時功率輸出曲線如圖12所示。從圖12(a)可以看出,在1.5 s前系統無功偏差率為22.96%,2.0 s應用虛擬阻抗策略后降低為4.92%,因此所提策略適用于容量不等的情形。

圖12 逆變器容量不等下輸出功率Fig.12 Power of different inverter capacity

案例1采用所提策略前后無功功率與電壓偏差率如表4所示。由表4可知所提策略可改善無功功率分配并實現電壓恢復。

表4 采用所提策略前后無功功率與電壓偏差率Table 4 Reactive power and voltage deviation of Case1 without and with proposed strategy

4.3 案例2:負荷投切

孤島微網中常有負載投切,因此需驗證所提策略不受負荷波動的影響。負荷投入場景設定如下:t∈[0,4.5) s時微網帶負載1運行,在4.5 s時接入負荷2;負荷切除場景設定如下:t∈[0,4) s時微網帶負荷1與2運行,在4.0 s時切除負荷2,無功功率如圖13所示。

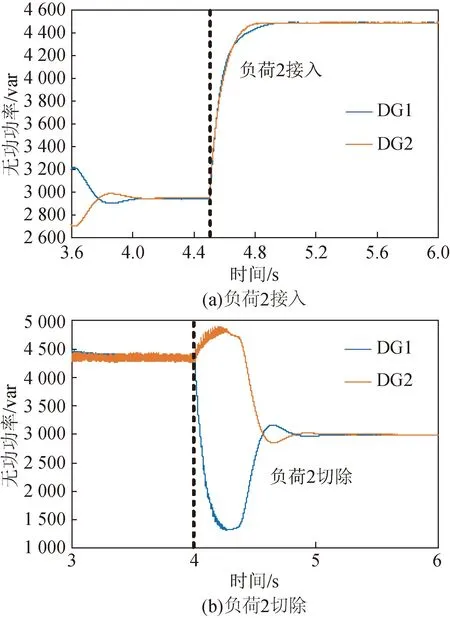
圖13 負荷投切下無功功率Fig.13 Reactive power of load switching

從圖13(a)可以看出,負荷2投入后0.3 s無功功率實現均分;從圖13(b)可以看出,負荷2切除后1.0 s實現無功功率均分。因此在實際中發生負荷突增或突減擾動時,GFL逆變器可按照剩余容量與GFM逆變器按比例增發相應無功。

4.4 案例3:即插即用

該場景是為模擬現實中DG從微網中斷開或接入的需求。設t∈[0,3.00] s微網包含DG1,DG2與DG3(GFM型)3個逆變器,其中DG3線路電感為2 mH,其余參數同DG1,1.50 s采用本文所提控制策略。t=3.00 s時切除DG3,無功功率曲線如圖14(a)所示。

圖14 切除與接入DG3無功功率Fig.14 Reactive power of DG3 been disconnected and connected

從圖14(a)可以看出,在約1.80 s時3個逆變器系統實現無功功率均分;t=3.00 s切除DG3后約0.30 s無功功率重新實現均分。

在接入DG3前需通過預同步控制環節使其角頻率,電壓幅值和相位與微網一致,盡力減小電流沖擊保證逆變器穩定并網[39-40],所得無功功率曲線如圖14(b)所示。在t=1.0 s時啟動預同步環節使角頻率與DG1一致,t=2.35 s將DG3接入系統并采用所提策略。從圖14(b)可以看出,當t=1.80 s時DG1與DG2實現無功功率均分,2.35 s時接入DG3,約0.40 s后重新實現無功功率均分。最終驗證所提策略適用于即插即用情形。

綜上所述,所提策略可適用于輸電線路阻抗不等且變化、逆變器容量不等、投切負荷以及即插即用場景。

5 結 論

本文提出一種基于自適應虛擬阻抗且適用于GFM與GFL逆變器主導微網系統的無功功率分配控制策略,可實現GFM與GFL逆變器間無功功率均分與電壓恢復。具體如下:

1) 采用倒下垂控制可使GFL逆變器具備無功功率下垂特性從而能夠參與功率二次調節,且所提控制策略可使異構逆變器間無功功率均分與電壓恢復不受輸電線路阻抗影響,MATLAB/Simulink仿真結果也表明該策略在逆變器容量不等、負荷投切與即插即用下仍具備適用性。

2) 無功偏差積分系數會影響無功功率的收斂過程,其值越大無功曲線響應速率越快,但系統阻尼隨之減小,應綜合考慮折中選取。

本文考慮GFL逆變器參與二次功率控制時未計及剩余容量,基于此種約束的優化無功功率分配策略是后續研究的重點。