橢圓曲線y2=7qx(x2-2)的正整數點

杜先存,趙正仙,邢怡然

(紅河學院 教師教育學院,云南 蒙自 661199)

橢圓曲線的整數點是數論中很重要的問題,關于橢圓曲線y=mx(x2-22n-1),m,n∈Z+的整數點問題已有多篇文獻報道[1-11],而對于橢圓曲線y2=7qx(x2-2)的整數點問題,目前還沒有相關結論,本文主要討論該橢圓曲線的整數點情況。

1 重要引理

引理1[12]a,b∈Z+,則方程ax4-by2=1至多有2組正整數解。

2 相關定理

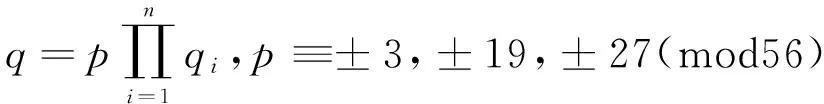
y2=7qx(x2-2)

(1)

除整數點(x,y)=(0,0)外至多有2個正整數點。

3 定理證明

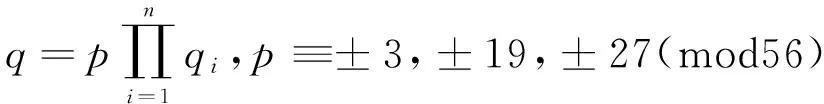
7qz2=x(x2-2)

(2)

因為gcd(x,x2-2)=1或2,故(2)式可分解為以下4種情況:

情形Ⅰx=ma2,x2-2=7nb2,z=ab,q=mn,gcd(a,b)=1,a,b,m,n∈Z+

情形Ⅱx=2ma2,x2-2=14nb2,z=2ab,q=mn,gcd(a,b)=1,a,b,m,n∈Z+

情形Ⅲx=7ma2,x2-2=nb2,z=ab,q=mn,gcd(a,b)=1,a,b,m,n∈Z+

情形Ⅳx=14ma2,x2-2=2nb2,z=2ab,q=mn,gcd(a,b)=1,a,b,m,n∈Z+

下面分別討論下面四種情形下(3)的正整數點的情況。

3.1 情形Ⅰ的討論

當n≠1時,若n含有素因子p,則x2-2=7nb2兩邊同時取模p,得

x2≡2(modp)

(3)

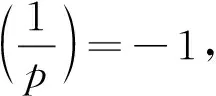
若n含有素因子qj(j=1,2,…,n),則x2-2=7nb2兩邊同時取模qj,得

x2≡2(modqj)

(4)

綜上有n≠1時情形Ⅰ不成立,即橢圓曲線(1)無正整數點。

當n=1時,x=ma2,x2-2=7nb2為x=qa2,x2-2=7b2。將x=qa2代入x2-2=7b2,化簡得q2a4-7b2=2,兩邊同時取模p,得

-7b2≡2(modp)

(5)

綜上有n=1時情形Ⅰ不成立,即橢圓曲線(1)無正整數點。

3.2 情形Ⅱ的討論

當n≠1時,若n含有素因子p,則x2-2=14nb2兩邊同時取模p,得

x2≡2(modp)

(3)

若n含有素因子qj(j=1,2,…,n),則x2-2=14nb2兩邊同時取模qj,得

x2≡2(modqj)

(4)

綜上有n≠1時情形Ⅱ不成立,即橢圓曲線(1)無正整數點。

當n=1時,x=2ma2,x2-2=14nb2為x=2qa2,x2-2=14b2。將x=2qa2代入x2-2=14b2,化簡得

2q2a4-7b2=1

(6)

由引理1知方程(6)至多有2個正整數解,則此時橢圓曲線(1)至多有2個正整數點。

3.3 情形Ⅲ的討論

當n≠1時,若n含有素因子p,則x2-2=nb2兩邊同時取模p,得

x2≡2(modp)

(3)

若n含有素因子qj(j=1,2,…,n),則x2-2=nb2兩邊同時取模qj,得

x2≡2(modqj)

(4)

綜上有n≠1時情形Ⅲ不成立,即橢圓曲線(1)無正整數點。

3.4 情形Ⅳ的討論

當n≠1時,若n含有素因子p,則x2-2=2nb2兩邊同時取模p,得

x2≡2(modp)

(3)

若n含有素因子qj(j=1,2,…,n),則x2-2=2nb2兩邊同時取模qj,得

x2≡2(modqj)

(4)

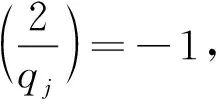
綜上有n≠1時情形Ⅳ不成立,即橢圓曲線(1)無正整數點。

當n=1時,x=14ma2,x2-2=2nb2為x=14qa2,x2-2=2b2。將x=14qa2代入x2-2=2b2,化簡得

98q2a4-b2=1

(8)

由引理1知方程(8)至多有2個正整數解,則此時橢圓曲線(1)至多有2個正整數點。

綜上所述,定理成立。