基于“數(shù)學化”思想對統(tǒng)領(lǐng)課教學的多維度探究

包雯

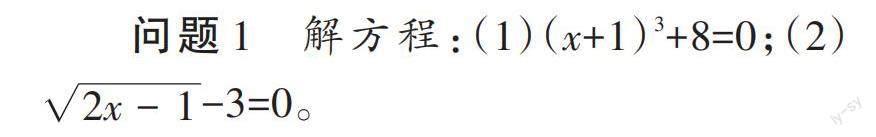
一、教學內(nèi)容分析

統(tǒng)領(lǐng)課是一章內(nèi)容正式授課的第一節(jié)課，對全章框架、內(nèi)容、方法、思維等要素進行梳理，是承載整章教學內(nèi)容的先導課，具有統(tǒng)攝作用，旨在讓學生“先見森林，再見樹木”。

一元二次方程知識量大，復雜程度高，是更深層次上對實際問題中含有未知數(shù)的等量關(guān)系的表達方式，也是繼續(xù)學習一元二次不等式、二次函數(shù)及二次曲線的重要基礎(chǔ)。教師要加強對單元統(tǒng)領(lǐng)課的重視和研究，從培養(yǎng)學生核心素養(yǎng)的角度讓學生會用數(shù)學的眼光觀察現(xiàn)實世界，會用數(shù)學的思維思考現(xiàn)實世界，會用數(shù)學的語言表達現(xiàn)實世界。

二、設(shè)計理念

弗賴登塔爾將“數(shù)學化”分為水平數(shù)學化和垂直數(shù)學化兩種形式。水平數(shù)學化，是學生可以運用教學工具發(fā)現(xiàn)和解答生活情境中的問題；垂直數(shù)學化，是在數(shù)學系統(tǒng)內(nèi)再組織的過程。簡單來說，水平數(shù)學化是從現(xiàn)實世界走進符號世界，而垂直數(shù)學化是在符號世界中前進。教師對兩種數(shù)學化重視程度有差異，會在教學實踐中發(fā)生權(quán)重分配上的偏差。因此，兩種不同維度的數(shù)學化如何合理地分配權(quán)重，也需要根據(jù)具體教學內(nèi)容進行微調(diào)。就一元二次方程統(tǒng)領(lǐng)課而言，教師既要引導學生提煉實際問題中的數(shù)學成分，將實際問題向數(shù)學問題轉(zhuǎn)化，讓學生經(jīng)歷“分析→提煉→抽象”的過程，實現(xiàn)水平數(shù)學化的順利過渡；也要引導學生對研究策略和路徑進行遷移，建立垂直數(shù)學化的探究路徑，培養(yǎng)學生的數(shù)學思維方式，滲透數(shù)學思想方法。

三、教學過程

1.水平數(shù)學化

（1）創(chuàng)設(shè)教學情境，讓學生學會用數(shù)學眼光觀察現(xiàn)實世界

情境 小明購買了16m的籬笆，計劃圍一個矩形花圃。看著12m的圍墻，小明陷入了沉思……

【設(shè)計意圖】設(shè)計的情境開放程度大，入口寬，學生極有可能“走”向二次函數(shù)。如何從函數(shù)一步步“走”進二次方程，對教師課堂應變能力是極大的考驗。如此開放的設(shè)計，是希望最大限度引導學生用“數(shù)學眼光”觀察現(xiàn)實世界，提出有“數(shù)學味道”的實際問題，將實際情境與數(shù)學表征進行轉(zhuǎn)化。

（2）設(shè)計問題串，讓學生學會用數(shù)學思維思考現(xiàn)實世界

師：怎樣圍才能使矩形花圃的面積最大？試一試。

生1（預設(shè)）：從充分利用圍墻的角度考慮，如圖1，當AB=2時， S最大，S=24。

師：這時面積是最大的嗎？

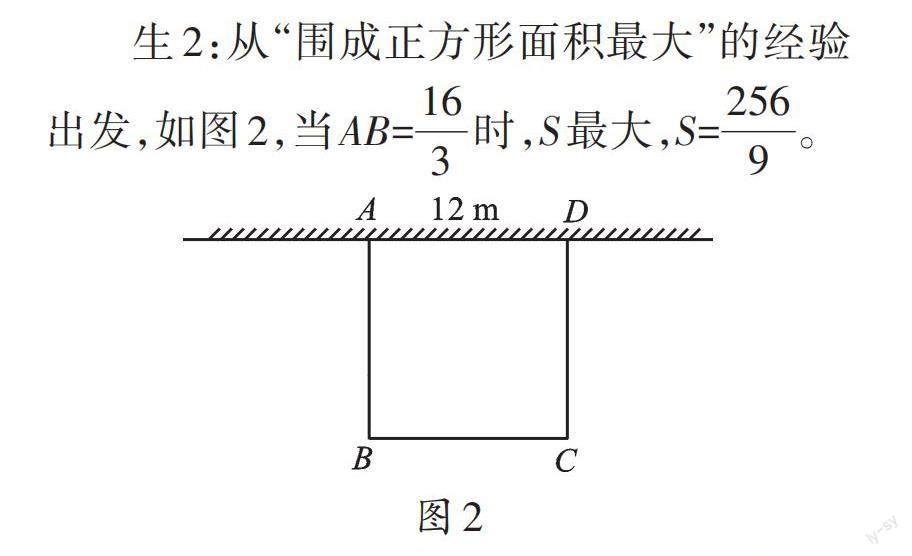
生2：從“圍成正方形面積最大”的經(jīng)驗出發(fā)，如圖2，當AB=[163]時，S最大，S=[2569]。

師：這是最大的面積嗎？還能圍成其他形式的矩形嗎？有多少種可能？

師：你還能找出比圖2面積更大的矩形嗎？試一試。

【設(shè)計意圖】如果僅停留在“最大化”的問題上，本題只能算是帶有數(shù)學味道的“生活化”問題。教師應順著學生的想法，沿著“最大化”這一優(yōu)化路徑，引導學生嘗試、探究，在反復試錯中找到解決問題的數(shù)學工具，促進學生深度思考。學生通過反復計算，在試圖找出“最大化”方案的過程中，將生活化問題抽象成數(shù)學問題，在這個過程中，學生思維已經(jīng)從“生活化”轉(zhuǎn)向“數(shù)學化”。

（3）建立數(shù)學模型，讓學生學會用數(shù)學語言表達現(xiàn)實世界

通過嘗試，學生發(fā)現(xiàn)，無論是“充分利用墻的長度”，還是“圍成正方形”，都不能使圍成的矩形面積最大。

生3：根據(jù)運用方程解決問題的經(jīng)驗，我們可以設(shè)AB=xm，BC=（16-2x）m，面積為x（16-2x）=-2x2+16x=-2（x-4）2+32，當x=4時，面積最大，為32。

【設(shè)計意圖】“圍花圃”這一情境的創(chuàng)設(shè)，讓學生經(jīng)歷從生活世界走向符號世界，經(jīng)歷將實際問題轉(zhuǎn)化為數(shù)學問題的過程。從“用數(shù)學的眼光觀察現(xiàn)實世界”，到“用數(shù)學的思維思考現(xiàn)實世界”，再到“用數(shù)學的語言表達現(xiàn)實世界”，學生結(jié)合已有經(jīng)驗形成功能更強、結(jié)構(gòu)更復雜的新模型。

2.垂直數(shù)學化

（1）從數(shù)學概念到新數(shù)學概念的平行結(jié)構(gòu)探究，完成“整式方程”體系的完整建構(gòu)

師：這是我們學過的方程嗎？我們學過哪些方程？你可以給這個方程下個定義嗎？整式方程的命名通常遵循什么規(guī)則？

【設(shè)計意圖】教師通過引導學生對一元二次方程概念內(nèi)涵的類比研究，滲透類比思想，使學生對方程中涉及的“多元”“高次”有了進一步認知，同時完善整式方程和分式方程的概念體系，為更多類型方程的探究奠定了基礎(chǔ)，也為探究一元二次方程提供了一致的探究路徑，進而推廣到對整式方程概念內(nèi)涵的探索。

（2）探究路徑的遷移

師：我們對一元二次方程可以進行哪些方面的研究？

【設(shè)計意圖】教師引導學生將方程的研究策略和研究路徑進行遷移，即：定義→解→解法→應用，確立“垂直數(shù)學化”這一預設(shè)目標，讓學生建立一般化的研究策略、路徑，對一元二次方程做進一步探究。

（3）在“消元”和“降次”兩個方面統(tǒng)一化歸思想

師：回顧其他方程的解法，你怎么求解一元二次方程？怎樣降次？這些“降次”的方法適用其他一元二次方程嗎？

【設(shè)計意圖】結(jié)合“消元”“化整”的經(jīng)驗，學生順理成章地將“化歸”思想遷移，“降次”應運而生。

（4）對比研究，完善方程“解法系統(tǒng)”的完整性建構(gòu)

問題1 解方程：（1）（x+1）3+8=0；（2）[2x-1]-3=0。

師：這些方程的解法有什么共同的數(shù)學思想嗎？

【設(shè)計意圖】從“一元”到“多元”、從“一次”到“高次”、從“有理”到“無理”，學生經(jīng)歷不同方程解法的對比分析過程，發(fā)現(xiàn)不同解法中蘊含著相同思想——“化歸”思想，完善方程“解法系統(tǒng)”的完整性建構(gòu)，實現(xiàn)數(shù)學思想的再度升華。

（5）建立方程與函數(shù)的聯(lián)系，培養(yǎng)學生數(shù)學“區(qū)塊鏈”意識

師：是否可以圍成比32m2更大的矩形呢？隨著x的變化，S也在變化，怎樣才能圍成最大矩形？

【設(shè)計意圖】回歸問題情境，讓學生體會方程是用來刻畫現(xiàn)實世界的模型，也是用于解決現(xiàn)實問題的數(shù)學工具。通過引導學生對數(shù)量關(guān)系中“變化而變化”的思考，學生主動挖掘新函數(shù)模型，建立方程和函數(shù)“區(qū)塊鏈”的意識。

四、結(jié)合教學實踐對統(tǒng)領(lǐng)課的再思考

1.一盞明燈破“暗處”

良好的統(tǒng)領(lǐng)課教學可以幫助學生建立知識框架，提高學習效率，厘清本章所涉及的基本數(shù)學問題、數(shù)學方法和數(shù)學思想。同時，學生可以站在一個更高的位置，縱觀全局，無論對水平知識體系的橫向遷移，還是對垂直知識體系的縱深推進，都能得心應手。統(tǒng)領(lǐng)課教學就是“先見林，再見樹”；如一盞“明燈”，為后續(xù)學習指明方向，它照亮了數(shù)學學習之路，讓學生更加明確做什么、怎樣做以及為什么。

2.添磚加瓦筑“新巢”

當然，統(tǒng)領(lǐng)課只明確學習主線和方向遠遠不夠，更應結(jié)合相互關(guān)聯(lián)的“區(qū)塊鏈”，引導學生主動對數(shù)學知識、數(shù)學模型及數(shù)學思想進行“鏈接”，對數(shù)學知識乃至整個數(shù)學系統(tǒng)溯本求源，在激發(fā)學生探究欲望的同時，也讓學生感受數(shù)學思想方法的美妙之處。通過一步步、一層層的探索，對比，聯(lián)結(jié)，數(shù)學知識系統(tǒng)變得更加完整，數(shù)學方法變得更加完善，學生逐漸養(yǎng)成獨特的“數(shù)學眼光”、深度的“數(shù)學思維”和精準的“數(shù)學表達”，從而最終落實數(shù)學核心素養(yǎng)的養(yǎng)成。

（作者單位：江蘇省南京一中明發(fā)濱江分校）