基于自適應調整哈里斯鷹優化算法求解機器人路徑規劃問題

黃霖，符強，童楠

基于自適應調整哈里斯鷹優化算法求解機器人路徑規劃問題

黃霖1，符強1，2*，童楠2

（1.寧波大學 信息科學與工程學院，浙江 寧波 315000； 2.寧波大學科學技術學院 信息工程學院，浙江 寧波 315300）（?通信作者電子郵箱fuqiang@nbu.edu.cn）

針對啟發式算法在機器人路徑規劃過程中存在路徑長度不穩定和易陷入局部極小點的問題，提出一種基于自適應調整哈里斯鷹優化（AAHHO）算法。首先，利用收斂因子調整策略，調節全局搜索階段和局部搜索階段的平衡，同時利用自然常數為底數，提高搜索效率和收斂精度；其次，在全局搜索階段，采用精英合作引導搜索策略，通過3個精英哈里斯鷹合作引導其他個體更新位置以提高搜索性能，通過3個最優位置加強種群間的信息交流；最后，通過模擬種內競爭策略增強哈里斯鷹跳出局部最優的能力。函數測試和機器人路徑規劃對比實驗結果表明，所提算法無論是函數測試還是機器人路徑規劃都優于IHHO（Improve Harris Hawk Optimization）和CHHO（Chaotic Harris Hawk Optimization）等對比算法，對于求解機器人的路徑規劃具有較好的有效性、可行性和穩定性。

機器人；路徑規劃；哈里斯鷹優化算法；收斂因子調整；精英合作引導搜索；種內競爭

0 引言

隨著機器人技術的快速發展，移動機器人廣泛應用于工業、醫療和農業等領域［1］。移動機器人的路徑規劃是移動機器人研究中一項關鍵性技術，移動機器人路徑規劃的目標是從起點到目標點之間尋找到一條無碰撞且代價低的路線。規劃有效且避障的路線一直是該技術的難題，國內外學者針對這一難題提出了許多路徑規劃方法［2］，例如A*（A star）［3］、人工勢場［4］、啟發式算法（群智能算法）［5］、神經網絡［6］、深度學習［7］和強化學習［8］等不同機制特點的技術及方法，其中具有尋優機制簡單、參數設置少、魯棒性強和全局搜索能力強等特點的啟發式算法通常被應用于機器人路徑規劃［9-10］。

Heidari等［11］提出一種新型啟發式算法——哈里斯鷹優化（Harris Hawk Optimization， HHO）算法。HHO算法參數少、原理簡單，且有較強的全局搜索能力，已經在車間調度［12］、圖像處理［13-16］、神經網絡訓練［17］和特征選擇［18-22］等方面有實際應用；但是與其他群智能算法［23］一樣，HHO算法存在收斂精度低、收斂較慢和較易陷入局部最優的缺點。針對這些不足，本文提出了自適應調整哈里斯鷹優化（Adaptive Adjusted HHO， AAHHO）算法。首先通過采用收斂因子的調整策略，利用指數函數收斂性能提高后期的收斂精度，并通過調整倍數和指數函數提高前期的全局搜索概率，從而增強算法的尋優能力；其次針對哈里斯鷹缺乏種群間的信息交流和全局搜索的盲目性，引入精英合作引導搜索策略，根據適應度值排名前3的3只哈里斯鷹帶領著種群更新位置，提高算法的搜索性能和效率；最后，因為引入了精英合作引導搜索策略，同時也增加了對精英哈里斯鷹以及算法自身種群對平均位置的依賴性，提高了陷入局部最優的概率，為了解決這一問題，加入了種內競爭策略，以增強跳出局部最優的能力。將AAHHO算法與對比算法分別進行函數測試比較并應用到機器人的路徑規劃，測試結果表明，AAHHO算法在尋優性能上和穩定性上都具有良好的優勢。

1 HHO算法

HHO算法中每只哈里斯鷹個體代表區間內的一個可行解（候選解）。通過探索和開發階段實現在區間內全局搜索和局部搜索獵物，而獵物的逃逸能量因子可以實現探索和開發的轉換。

1.1　探索階段

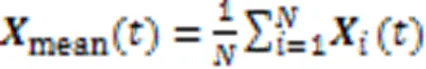
其中為種群數。

1.2　探索階段與開發階段的轉換

在逃跑過程中，獵物的逃逸能量不斷地減少，當逃逸能量減小為一定數值時，哈里斯鷹會采取策略的轉換，從探索階段的全局搜索轉換為開發階段的局部搜索。逃逸能量因子的公式為：

1.3　開發階段

1.3.1軟圍攻

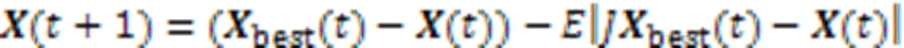
1.3.2硬圍攻

1.3.3漸進式快速俯沖軟圍攻

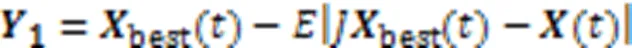
1.3.4漸進式快速俯沖硬圍攻

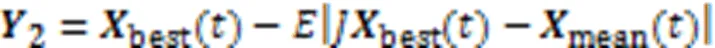
2 AAHHO算法

在HHO中，探索階段和開發階段轉換始終存在矛盾，在迭代前期可能出現一定概率的局部搜索，導致HHO算法容易陷入局部最優。通過提出收斂因子調整策略，提高算法前期全局搜索的概率，降低算法前期進行局部搜索的概率，在一定程度上避免早熟收斂。在探索階段，HHO算法采用隨機哈里斯鷹個體更新位置，缺乏種群間的相互交流，而且在更新位置時，步長設置過長，導致位置更新“失效”。通過引入精英合作引導搜索策略，讓精英哈里斯鷹引導其他個體更新位置；同時增加種群間的信息交流，利用精英合作引導式搜索控制過大的步長。HHO算法在更新時，比較依賴種群間的平均位置，在轉換階段時，因搜索不足容易導致陷入局部最優，通過引入種內競爭策略，在一定程度上能夠幫助跳出局部最優。

2.1　收斂因子調整策略

HHO算法與AAHHO算法的逃逸能量對比如圖1所示。從圖1中可以看出：AAHHO算法前期逃逸能量的值比HHO算法大，降低了前期出現局部搜索的概率；AAHHO算法后期逃逸能量的值比HHO算法小，提高了后期的收斂精度。AAHHO算法打破了HHO算法以區間的范圍，增大范圍而不改變逃逸能量值以1和0.5為界限，以此增大前期全局搜索的概率。

2.2　精英合作引導搜索策略

哈里斯鷹之所以獨特，就在于它可以跟其他家庭成員合作捕食從而進化出創新的團隊追逐能力。在哈里斯鷹種群內之間存在階層，利用種群內階級，而選擇適應度最好的三只精英哈里斯鷹進行引導式全局搜索：一方面，增加了種群間的信息交流；另一方面，通過精英引導以此提高哈里斯鷹全局搜索的性能。

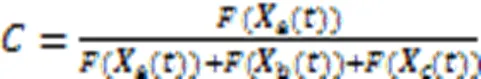
2.3　種內競爭策略

從生態學的角度來看，種內競爭能夠保留更加優秀和更加強壯的個體，使得衍生出更優秀的精英。通過模擬種內競爭策略來使得資源更有效的利用，為了更好模擬作如下假設：

1）在開發階段每一輪迭代都能獲取到食物。

2）食物量只夠一只哈里斯鷹享用。

3）獲得食物的為適應度值最高的哈里斯鷹，而未獲得食物的哈里斯鷹則會遭到適應度值高的哈里斯鷹驅逐。

哈里斯鷹為了能夠更好地享用食物，針對威脅度高的哈里斯鷹作出驅逐，而面對威脅度低的哈里斯鷹戒備心會有所降低，其數學模型為：

通過驅逐因子擴大搜索范圍，同時一定程度上能夠跳出局部最優。種內競爭策略是通過適應度值占比進行調節。適應度值越接近驅逐因子越大。

2.4　AAHHO算法流程

綜上所述，本文改進HHO算法，利用3種相互聯系的策略，提出了AAHHO算法。算法的流程如下。

步驟2 計算種群的適應度值。

步驟3 根據式（14），計算獵物的逃逸能量。

根據式（1）和式（15）更新位置

否則

通過式（19）模擬種內競爭，更新哈里斯鷹位置

步驟4 重復步驟2～3，直至達到最大迭代次數。

步驟5 輸出最優解。

2.5　復雜度分析

表達式的3個部分分別代表計算適應度值、位置更新和種內競爭策略，因此AAHHO算法的時間復雜度為：

3 仿真實驗與結果分析

本文仿真環境為Intel i7-8550U（1.8 GHz）處理器和8 GB運行內存，程序在Matlab 2018b仿真平臺運行。為了測試改進算法的優化性能，將AAHHO算法與HSCA（Hybrid Sine Cosine Algorithm， HSCA）［9］、TGWO（Tent-initialized Grey Wolf Optimization， TGWO）［5］、HHO算法［11］、IHHO（Improved HHO）算法［12］和CHHO（Chaotic HHO）算法［25］進行對比測試。

3.1　測試函數

為了更好地體現改進算法的性能，引用15個CEC標準測試函數對本文改進算法進行分析比較，通過單峰函數測試算法的收斂精度和速度，通過多峰函數測試算法的跳出局部最優解的能力，兩者結合檢驗算法的尋優性能。測試函數如表1所示。

表1　測試函數

為了測試的公平性，將各個算法的種群數都設置為30，迭代次數設置為500，分別單獨進行30次實驗，并統計30次實驗得到的結果的平均值（AVG）和標準差（STD），實驗測試結果如表2所示。

通過收斂曲線，可以更直觀地看出算法的尋優性能，6種算法測試函數的收斂曲線如圖2所示。圖2（a）～（f）為單峰測試函數的收斂曲線，通過與其他5種算法收斂曲線對比可以看出，圖2（a）～（c）中AAHHO算法在精英合作引導策略和收斂因子調整策略的作用下，能快速找到最優解，收斂更快，收斂精度更高；圖2（d）～（f）中，AAHHO算法在前期搜索時也曾陷入局部最優，但后期的種內競爭使之能夠擺脫。圖2（g）～（o）為多峰測試函數的收斂曲線，其中：對于圖2（g）（j）（k）（m），AAHHO算法相較于HHO、IHHO和CHHO算法更接近最優解；對于圖2（h）（i）（l），AAHHO算法的收斂和尋找最優解相較于其他5種算法更快；對于圖2（n），TGWO一直困入局部最優，其他算法前期收斂都快；對圖2（o），AAHHO算法能夠逼近最優值，明顯優于其他5種算法。

表2　6種算法在固定迭代次數下尋優結果比較

注：AVG表示均值，STD表示標準值。

由實驗對比結果分析可知，AAHHO算法表現了較好的優化性能，尋優精度、尋優穩定性和收斂速度優于其他5種性能優越的代表性對比算法。

3.2　基于AAHHO算法的機器人路徑規劃

為了更好地展現AAHHO算法優勢，將AAHHO算法應用于機器人的路徑規劃問題。很多學者將插值的方式應用于機器人的路徑規劃［10，26］，路徑較短，但是機器人在移動過程中需要更多的判斷和調整；而采用直線，只需設定幾個節點直行，在節點旋轉角度即可，不需要較多復雜的計算判斷過程。

3.2.1環境建模與適應度函數

在建立模型前，先做如下假設：

1）將機器人看作一個無質量和無大小的質點。

2）移動的環境設置為二維。

3）障礙物為圓形，空間只有分布隨意且若干個障礙物。

3.2.2基于AAHHO算法的機器人路徑規劃流程

基于AAHHO算法機器人路徑規劃的算法具體流程如下：

步驟1 根據具體環境設置節點數和最大迭代次數，確定機器人起點坐標和終點坐標。

步驟3 根據AAHHO算法和適應度函數更新每只哈里斯鷹的坐標位置。

步驟4 重復步驟3，直到達到最大迭代次數。

步驟5 輸出最優路徑。

圖2　15個基準函數收斂曲線

3.2.3機器人的路徑規劃

不同場景的路徑規劃和收斂曲線對比如圖3所示。

場景一障礙物較少，故設它的路徑節點數為2，終點坐標為（4，4）和起點坐標為（0，0）。

場景二障礙物較多，故設它的路徑節點數為3，終點坐標為（6，6）和起點坐標為（0，0）。

表3分別統計了6種算法在不同場景下的路徑長度的最優值、最差值、平均值和方差，可以看出，AAHHO算法的搜索性能和穩定都較好。從圖3（b）可以看出，對于HSCA算法，通過反向學習初始化種群、模因分組和種群進化等策略，在初始路徑和尋優上具有部分優勢，但在收斂性能上存在缺陷。

表36種算法在不同場景下的路徑比較

Tab.3　Path comparison of six algorithms in different scenarios

對于TGWO算法，通過控制參數調整、動態權重因子和適應度比例系數等策略，在穩定性上和收斂性能上是有優勢的。對于CHHO算法，采用高斯混沌映射，作用于探索、開發階段和逃逸能量，對收斂精度有一定的改善。對于IHHO算法，通過兩個精英個體引導其他個體，作用于全局搜索，使它的搜索性能有一定的改善。AAHHO算法在全局搜索上得益于精英合作引導搜索策略對節點坐標的把控較好，通過收斂因子的調節，在增大前期的全局搜索能力的同時，提高了后期的收斂精度，使路徑規劃的尋優和穩定性都較好。

圖3　不同場景的路徑規劃和收斂曲線對比

4 結語

為了更好地求解機器人的路徑規劃問題和改進HHO算法的性能，本文針對HHO算法收斂精度不高、易陷入局部最優等存在的不足進行改進，提出AAHHO算法。首先，引入精英合作引導搜索策略，提高種群之間的相互交流和搜索性能，引入了收斂因子調整策略，提高前期全局搜索概率，利用指數函數特性提高后期的收斂精度；其次，加入了種內競爭策略，提高陷入局部極值的擺脫能力；再次，通過與5種其他對比算法進行測試函數實驗對比分析，仿真結果驗證了AAHHO算法具有較好的收斂精度和尋優性能；最后，通過將AAHHO算法與其他5種算法進行機器人路徑規劃的對比，驗證了本文算法在求解機器人路徑規劃問題的優越性和穩定性。下一步將繼續改進哈里斯鷹算法的尋優性能，研究新的改進算法并應用于機器人的路徑規劃和更多復雜的實際問題的優化。

[1] DENG X， LI R， ZHAO L， et al. Multi-obstacle path planning and optimization for mobile robot［J］. Expert Systems with Applications， 2021， 183： 115445.

[2] 徐小強，王明勇，冒燕.基于改進人工勢場法的移動機器人路徑規劃［J］.計算機應用，2020，40（12）：3508-3512.（XU X Q， WANG M Y， MAO Y.Path planning of mobile robot based on improved artificial potential field method ［J］. Journal of Computer Applications， 2020，40 （12）： 3508-3512.）

[3] HUANG H， LI Y， BAI Q. An improved A star algorithm for wheeled robots path planning with jump points search and pruning method ［J］. Complex Engineering Systems， 2022， 2（3）： 11.

[4] 李偉，金世俊.基于人工勢場法和啟發式采樣的最優路徑收斂方法［J］.計算機應用，2021，41（10）：2912-2918.（LI W， JIN S J . Optimal path convergence method based on artificial potential field method and informed sampling ［J］. Journal of Computer Applications， 2021，41（10）： 2912-2918.）

[5] 劉志強，何麗，袁亮，等.采用改進灰狼算法的移動機器人路徑規劃［J］.西安交通大學學報，2022，56（10）：49-60.（LIU Z Q， HE L， YUAN L， et al. Path planning of mobile robot based on TGWO algorithm ［J］. Journal of Xi’an Jiaotong University， 2022，56（10）： 49-60.）

[6] WANG J， LIU J， CHEN W， et al. Robot path planning via neural-network-driven prediction［J］. IEEE Transactions on Artificial Intelligence， 2021， 3（3）： 451-460.

[7] WU P， CAO Y， HE Y， et al. Vision-based robot path planning with deep learning［C］// Proceedings of the 11th International Conference on Computer Vision Systems. Cham： Springer， 2017： 101-111.

[8] ABDI A， ADHIKARI D， PARK J H. A novel hybrid path planning method based on Q-learning and neural network for robot arm ［J］. Applied Sciences， 2021， 11（15）： 6770.

[9] 馬瑩瑩，杜暖男.基于改進正余弦算法的機器人路徑規劃［J］.重慶交通大學學報（自然科學版），2021，40（9）：17-23.（MA Y Y， DU N N. Robot path planning based on the improved sine cosine algorithm ［J］. Journal of Chongqing Jiaotong University （Natural Sciences）， 2021，40 （9）： 17-23.）

[10] 劉景森，吉宏遠，李煜.基于改進蝙蝠算法和三次樣條插值的機器人路徑規劃［J］.自動化學報，2021，47（7）：1710-1719.（LIU J S， JI H Y， LI Y. Robotic path planning based on improved bat algorithm and cubic spline interpolation ［J］. Acta Automatica Sinica， 2021，47 （7）： 1710-1719.）

[11] HEIDARI A A， MIRJALILI S， FARIS H， et al. Harris hawks optimization： algorithm and applications ［J］. Future Generation Computer Systems， 2019， 97： 849-872.

[12] LIU C. An improved Harris hawks optimizer for job-shop scheduling problem［J］. The Journal of Supercomputing， 2021， 77： 14090-14129.

[13] JIA H， LANG C， OLIVA D， et al. Dynamic Harris hawks optimization with mutation mechanism for satellite image segmentation ［J］. Remote Sensing， 2019， 11（12）： 1421.

[14] GOLILARZ N A， MIRMOZAFFARI M， GASHTEROODKHANI T A， et al. Optimized wavelet-based satellite image de-noising with multi-population differential evolution-assisted Harris hawks optimization algorithm［J］. IEEE Access， 2020， 8： 133076-133085.

[15] JIA H， PENG X， KANG L， et al. Pulse coupled neural network based on Harris hawks optimization algorithm for image segmentation ［J］. Multimedia Tools and Applications， 2020， 79： 28369-28392.

[16] BANDYOPADHYAY R， KUNDU R， OLIVA D， et al. Segmentation of brain MRI using an altruistic Harris hawks’ optimization algorithm［J］. Knowledge-Based Systems， 2021， 232： 107468.

[17] CAMPBELL M O N. The Great Eagles： Their Evolution， Ecology and Conservation ［M］. Boca Raton： CRC Press， 2022：347-363.

[18] TURABIEH H， AZWARI S A， ROKAYA M， et al. Enhanced Harris hawks optimization as a feature selection for the prediction of student performance ［J］. Computing， 2021， 103： 1417-1438.

[19] ABDEL-BASSET M， DING W， EL-SHAHAT D. A hybrid Harris hawks optimization algorithm with simulated annealing for feature selection ［J］. Artificial Intelligence Review， 2021， 54： 593-637.

[20] SIHWAIL R， OMAR K， ARIFFIN K A Z， et al. Improved Harris hawks optimization using elite opposition-based learning and novel search mechanism for feature selection ［J］. IEEE Access， 2020， 8： 121127-121145.

[21] AL-SAFI H， MUNILLA J， RAHEBI J. Patient privacy in smart cities by blockchain technology and feature selection with Harris Hawks Optimization （HHO） algorithm and machine learning ［J］. Multimedia Tools and Applications， 2022， 81： 8719-8743.

[22] ZHANG Y， LIU R， WANG X， et al. Boosted binary Harris hawks optimizer and feature selection ［J］. Engineering with Computers， 2021， 37： 3741-3770.

[23] CHAKRABORTY A， KAR A K. Swarm intelligence： a review of algorithms ［M］// Nature-Inspired Computing and Optimization 10. Cham： Springer， 2017： 475-494.

[24] BARTHELEMY P， BERTOLOTTI J， WIERSMA D S. A Lévy flight for light ［J］. Nature， 2008， 453： 495-498.

[25] GEZICI H， LIVATYALI H. Chaotic Harris hawks optimization algorithm ［J］. Journal of Computational Design and Engineering， 2022， 9（1）： 216-245.

[26] 劉景森，袁蒙蒙，李煜.基于改進的樽海鞘群算法求解機器人路徑規劃問題［J］.計算機研究與發展，2022，59（6）：1297-1314.（LIU J S， YUAN M M， LI Y. Robot path planning based on improved salp swarm algorithm ［J］. Journal of Computer Research and Development， 2022，59（6）： 1297-1314.）

Solving robot path planning problem by adaptively adjusted Harris hawk optimization algorithm

HUANG Lin1， FU Qiang1，2*， TONG Nan2

（1，，315000，；2，，315300，）

Aiming at the problem that the heuristic algorithms have unstable path lengths and are easy to fall into local minimum in the process of robot path planning， an Adaptively Adjusted Harris Hawk Optimization （AAHHO） algorithm was proposed. Firstly， the convergence factor adjustment strategy was used to adjust the balance between the global search stage and the local search stage， and the natural constant was used as the base to improve the search efficiency and convergence accuracy. Then， in the global search phase， the elite cooperation guided search strategy was adopted， by three elite Harris hawks cooperatively guiding other individuals to update the positions， so that the search performance was enhanced， and the information exchange among the populations was enhanced through the three optimal positions. Finally， by simulating the intraspecific competition strategy， the ability of the Harris hawks to jump out of the local optimum was improved. The comparative experimental results of function testing and robot path planning show that the proposed algorithm is superior to comparison algorithms such as IHHO（Improve Harris Hawk Optimization） and CHHO（Chaotic Harris Hawk Optimization）， in both function testing and path planning， and it has better effectiveness， feasibility and stability in robot path planning.

robot; path planning; Harris Hawk Optimization (HHO) algorithm; convergence factor adjustment; elite cooperation guided search; intraspecific competition

This work is partially supported by Ningbo Natural Science Foundation （2021J135）.

HUANG Lin， born in 1997， M.S. candidate. His research interests include swarm intelligence algorithm， machine learning.

FU Qiang， born in 1975， Ph. D.， associate professor. His research interests include swarm intelligence algorithm， machine learning.

TONG Nan， born in 1981， M.S.， lecturer. Her research interests include path planning， swarm intelligence algorithm.

TP242； TP301.6

A

1001-9081（2023）12-3840-08

10.11772/j.issn.1001-9081.2022121847

2022?12?13；

2023?03?03；

2023?03?06。

寧波市自然科學基金資助項目（2021J135）。

黃霖（1997—），男，江西贛州人，碩士研究生，主要研究方向：群智能算法、機器學習；符強（1975—），男，江西贛州人，副教授，博士，CCF會員，主要研究方向：群智能算法、機器學習；童楠（1981—），女，浙江紹興人，講師，碩士，主要研究方向：路徑規劃、群智能算法。