高中數學數列通項公式求解技巧

余 濤

(杭州市富陽區江南中學,浙江 杭州 311421)

高中數學數列通項公式的求解一直是教學的重難點,其求解技巧的靈活性較強,通常較難被學生掌握.為了幫助學生更好地把握數列通項公式的求解,文章匯總了不同類型的數列通項公式實例求解技巧,幫助學生在具體應用中去感受.

1 公式法

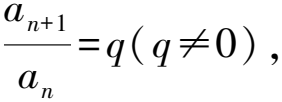
例1已知等差數列{an}符合a1+a2=10,a4-a3=2.

(1)求{an}的通項公式;

(2)設等比數列{bn}滿足b2=a3,b3=a7,求b6與數列{an}的第幾項相等?

解析(1)令等差數列{an}的公差為d,因為a4-a3=2,所以d=2.

因為a1+a2=10,所以2a1+d=10.所以a1=4.

綜上,an=2n+2(n=1,2,…).

(2)令等比數列{bn}的公比是q,因為b2=a3=8,b3=a7=16,所以q=2,b1=4.所以b6=4×26-1=128.由128=2n+2,得n=63[1].

由此可知,b6與數列{an}的第63項相等.

2 累加法

針對隸屬于an=an-1+f(n)類型的遞推式,可以通過移項取相鄰兩項的差,從而得到一種函數關系an-an-1=f(n),再采用代入方法累加每個遞推式使之相互抵消后,又可以得到一種只具有a1,an的遞推式,將得到目標數列的通項公式.一般可采用數列求和、錯位相減、裂項相消等技巧實現化解.

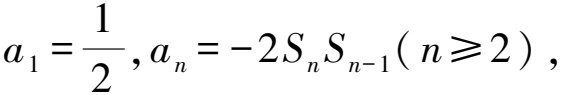
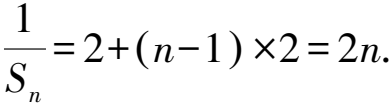
因為an=Sn-Sn-1(n≥2),

3 累乘法

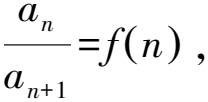
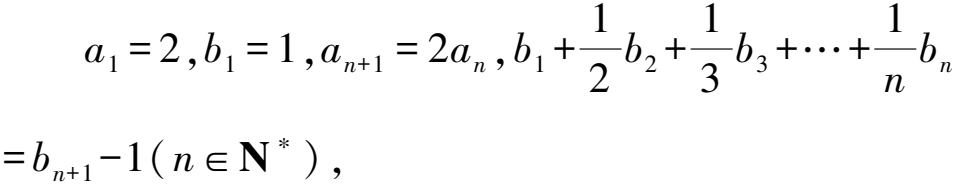
解析由a1=2,an+1=2an,得an=2n(n∈N*).當n=1時,b1=b2-1,所以b2=2.

所以當n≥2時,

同時因為b1=1,b2=2,所以bn=n.

4 數學歸納法

首先計算數列的前幾項,然后觀察an和n的關系并猜想數列通項公式,最后通過數學歸納法予以驗證,確定所猜想的數列通項公式成立于所有項數條件下.

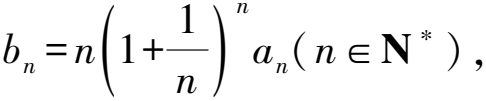
由此推測cn=(n+1)n(n∈N*).

通過數學歸納法進行證明,具體過程如下:

(1)當n=1時,左邊=右邊=2,等式成立.

(2)假設當n=k時等式成立,則

=[(k+1)+1]k+1.

所以,當n=k+1時,等式成立,結合(1)(2)可知,Cn=(n+1)n對所有正整數n均成立.

5 對數變換法

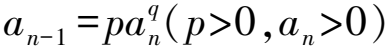
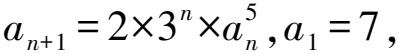
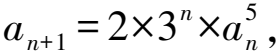
所以lgan+1=lg2+nlg3+5lgan.

令lgan+1+c(n+1)+d=5(lgan+cn+d),

則lgan+1=5lgan+4d+4cn-c.

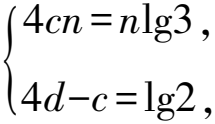
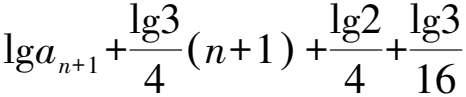
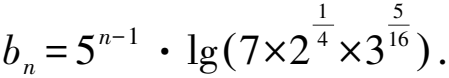
得到:

6 構造法

例6已知數列{an}滿足a1=1,an=3an-1-2n2-1(n≥2),求an.

解析因為an=3an-1+2n2-1(n≥2),令an+xn2+yn+z=3[an-1+x(n-1)2+y(n-1)+z],

整理,得

an=3an-1+2xn2+(-6x+2y)n+(3x-3y+2z).

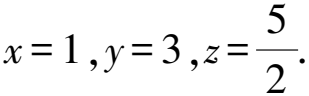
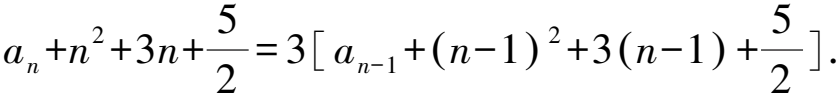
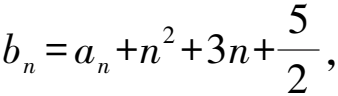
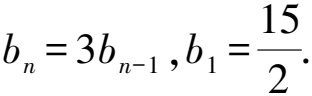
本文主要研究了高中數學數列通項公式的求解技巧,不同求解技巧應用了不同的數學思想,在公式法中呈現的是一種分類討論思維,數學歸納法則呈現了一種回歸整理思想,剩余技巧呈現的則是轉化化歸的思想.