探索變式訓(xùn)練在數(shù)學(xué)課堂教學(xué)中的應(yīng)用
周鏡輝
一、試題分析和反思
廣東省中山市2020-2021學(xué)年八年級數(shù)學(xué)下學(xué)期期末水平測試卷壓軸題(第25題),題目靈活多變,知識點綜合,有深度,對于考察訓(xùn)練學(xué)生對所學(xué)知識的綜合應(yīng)用能力,以及培養(yǎng)學(xué)生分析能力和發(fā)散思維很有幫助。題目如下:
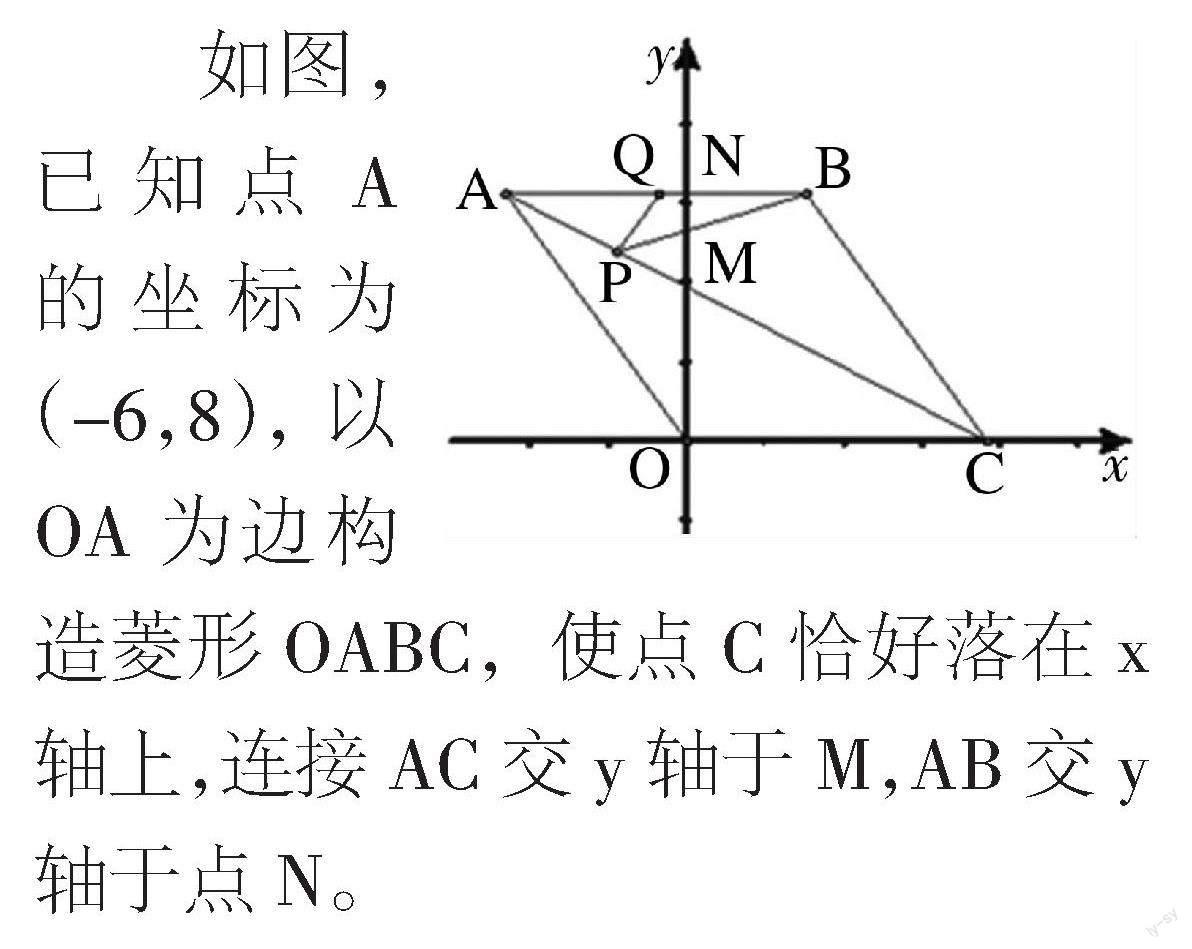
如圖,已知點A的坐標(biāo)為(-6,8),以O(shè)A為邊構(gòu)造菱形OABC,使點C恰好落在x軸上,連接AC交y軸于M,AB交y軸于點N。
(1)求直線AC的解析式;
(2)點Q為AB的中點,點P為線段AC上一動點,△PQB周長最小時,求點P的坐標(biāo)并求出△PQB周長的最小值。
題目只有菱形和點A的坐標(biāo)這兩個條件,很多同學(xué)無從下手。從我們學(xué)校情況來看,能靈活應(yīng)用八年級上冊將軍飲馬問題(最短路徑問題)的知識解答本題的同學(xué)比較少。將軍飲馬問題出現(xiàn)在人教版八年級上冊第十三章末的課題學(xué)習(xí)之問題1,是學(xué)生在學(xué)習(xí)了垂直平分線和軸對稱變換后各知識的綜合應(yīng)用。在教學(xué)中教師往往不夠重視,沒有挖掘它在圖形變換中的價值,進(jìn)行充分的變式訓(xùn)練。學(xué)生沒有真正理解好其內(nèi)在的圖形及數(shù)量關(guān)系。所以過一段時間后,遇到較綜合的問題時,便不能觸類旁通,因此變得束手無策。
二、變式訓(xùn)練開拓解題思路
在將軍飲馬問題(最短路徑問題)的教學(xué)過程中,教師在講解完問題1(人教版八年級上冊第85頁)時,即便是作圖也不要只局限于對稱軸為水平直線的作圖。
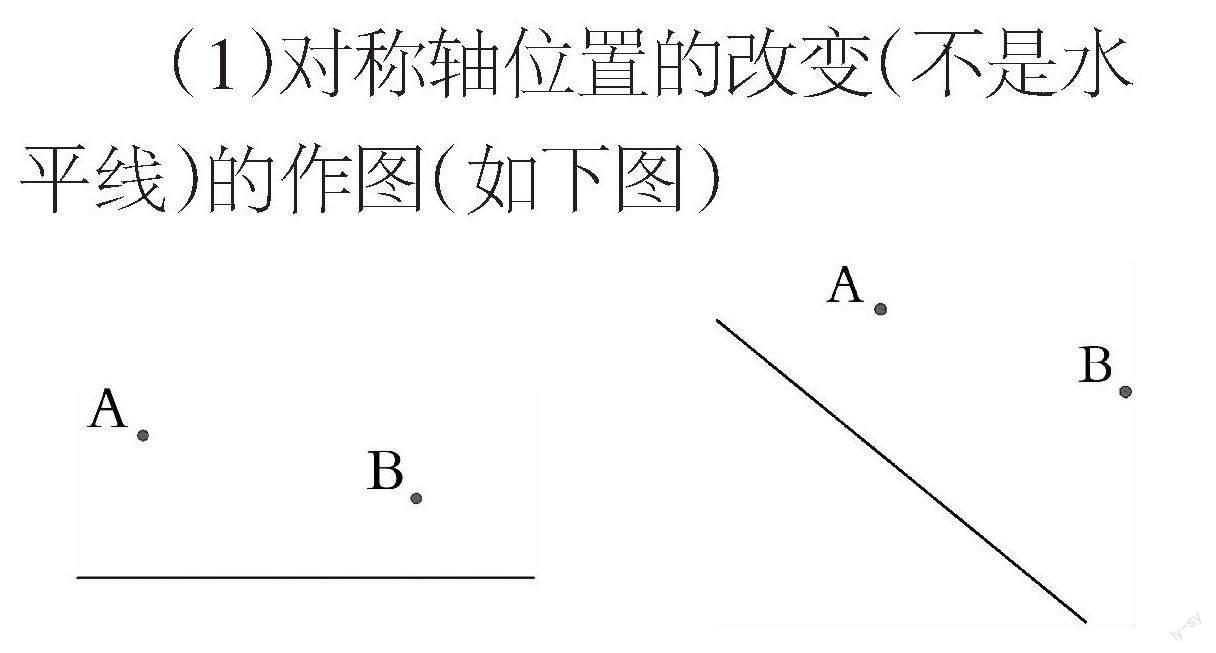
(1)對稱軸位置的改變(不是水平線)的作圖(如下圖)
(2)與剛學(xué)過的等腰和等邊三角形相結(jié)合
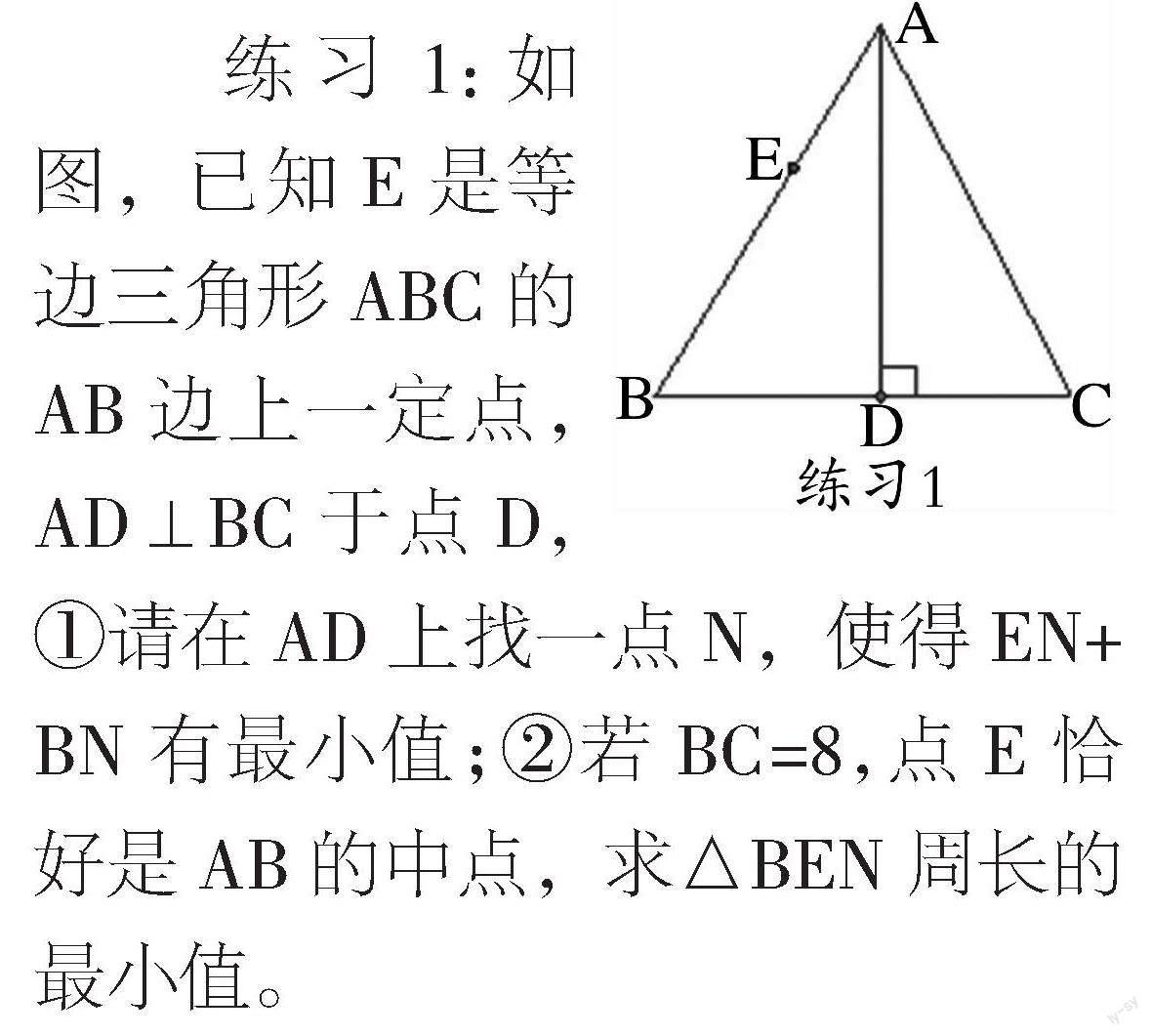
練習(xí)1:如圖,已知E是等邊三角形ABC的AB邊上一定點,AD⊥BC于點D,①請在AD上找一點N,使得EN+BN有最小值;②若BC=8,點E恰好是AB的中點,求△BEN周長的最小值。
(3)與矩形或正方形相結(jié)合
練習(xí)2:如圖,正方形ABCD的AB邊上有一點E,如何在AC上找到一點F,使得點F到點E,B的距離的和最短?
(4)與圓或扇形相結(jié)合
練習(xí)3:如圖,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于點D,點E為半徑OB上一動點,若OB=2,則陰影部分周長的最小值是?????? 。
三、設(shè)計變式訓(xùn)練時常用的形式
(一)一題多問
做完例題后直接在原題后再添加新問題,變題目的1問為2問、3問……
如上面的練習(xí)2:在講解完本題時可以直接在題后再添加新問題:
1.已知正方形ABCD的邊長為5,點E是線段AB的三等分點,求點F到點E,B的距離和的最小值;
2.求第2問中△BEF周長的最小值。
通過這樣的練習(xí),加強(qiáng)學(xué)生對知識的融會貫通和靈活運用,循序漸進(jìn),層層深入,不斷深化知識。
(二)變換題目的題設(shè)與結(jié)論
通過對比練習(xí),加深學(xué)生對十字相乘法的基本原理的認(rèn)識。并且對整式的乘法和因式分解這兩個知識間的內(nèi)在聯(lián)系和區(qū)別理解得更準(zhǔn)確,培養(yǎng)學(xué)生綜合和歸納的能力。
(三)一題多變
通過改變題目中的條件或結(jié)論,訓(xùn)練學(xué)生的發(fā)散思維,從易到難層層遞進(jìn),學(xué)生不但容易理解和掌握,還記憶深刻,開拓了解題思路,培養(yǎng)了探索意識。
(四)一題多解
數(shù)學(xué)很多題目往往都不止一種解法,教師在講解或展示完一種解法時可以多問問同學(xué)們還有沒有其他方法,學(xué)生們的解題思路往往比老師還豐富,老師要有意識地培養(yǎng)學(xué)生的這種發(fā)散思維和創(chuàng)新意識,不要局限于某種“標(biāo)準(zhǔn)解法”。
(五)一解多題
即用相同的知識點,相同或相似的解題方法和步驟解答不同的練習(xí)題。如上文中將軍飲馬問題(最短路徑問題)教學(xué)過程中,所設(shè)計的幾道變式訓(xùn)練題。一解多題在初三的專題學(xué)習(xí)中應(yīng)用非常廣泛。當(dāng)然,教學(xué)中在學(xué)生做完練習(xí)后,教師還要及時引領(lǐng)學(xué)生總結(jié),歸納方法,總結(jié)解題規(guī)律,真正做到融會貫通。
責(zé)任編輯? 李少杰

