基于BP神經網絡的蘭州新區現代有軌電車適用性評價

柴海華

摘 要：在綜合考慮蘭州新區現代有軌電車線網規劃的基礎上，基于BP神經網絡建立現代有軌電車適用性研究分析訓練模型，利用Matalab軟件實現神經網絡學習過程，根據訓練結果，對蘭州新區現代有軌電車適用性進行評價。

關鍵詞：BP神經網絡 有軌電車 適用性

1 BP神經網絡適用性評價

1.1 BP神經網絡結構

BP神經網絡結構形式多樣，在一般工程應用中，常采用多層結構形式，BP神經網絡結構多層形式主要是由輸入層、輸出層和若干個隱含層組成的多層感知器，層與層之間的關系是互連的，而同一層單元之間是互不連接的。多層感知器和BP神經網絡結構強調的是兩個不同的概念，多層感知器是指神經網絡結構由相互連接的多層組成，而BP神經網絡結構是指神經網絡采用誤差反向傳播的學習算法。但在進行權值調整學習訓練時，大多數情況下多層感知器采用誤差反向傳播的學習算法。從這個角度來講，多層感知器和BP神經網絡結構沒有太大的區別，經常指一種網絡，即BP神經網絡結構。

1.2 BP神經網絡結構特點

（1）多層性。BP神經網絡是由輸入層、輸出層和若干個隱含層組成的多層感知器，層與層之間的關系是互連的，而同一層單元之間是互不連接的。

（2）可微性。

BP神經網絡的傳遞函數是線性傳遞函數，其中x的取值范圍為整個實數域，f（x）的取值范圍是0到1之間，在具體計算時根據實際情況確定參數范圍。

2 BP神經網絡應用

BP神經網絡是目前應用頻率最高的神經網絡，其非線性映射能力比較強大，能夠集中反映神經網絡中最完美的內容[1]。在以前的神經網絡訓練模型中主要以單層為主，經過多年的發展，多層網絡學習訓練模型得以實現，而在實際應用中，以BP神經網絡學習訓練模型為主。

BP神經網絡訓練模型的傳播形式主要有前向傳播和誤差反向傳播兩種形式，所謂的前向傳播是指對于一個給定的輸入模式，先到達輸入層再到達隱藏層，在隱藏層經過一系列的處后形成一個輸出模式，這種傳播模式是一個逐層狀態不斷更新的過程；所謂的誤差反向傳播是指在輸入輸出過程中，期望輸出模式和輸出響應之間存在一定的誤差，不符合輸出模式要求，遇到類似情況時，前向傳播模式不能繼續進行，輸出模式會隨之轉為誤差反向傳播，在這種模式中，誤差值會沿著連接通路分層傳至更層級并對誤差值進行修正，直至滿足要求。BP神經網絡訓練的過程就是前向傳播和誤差反向傳播不斷重復迭新的過程，當精度滿足要求時，BP神經網絡訓練完成，主要包括配置階段、訓練階段和分類階段三個階段，三個階段之間既相互有區別，又相互之間有著緊密的聯系。

3 BP神經網絡評價模型的建立

BP神經網絡評價模型的建立關鍵在于網絡層數的合理確定和各獨立層神經元數的有序配置，前人研究表明，BP神經網絡的隱含層應當是一個可以用任意精度表示的連續函數，基于這樣的結論，可以將隱含層基本設置為一層[2-3]。

多層單元計算格式按下列式子計算

其中：j=0，1，2，…，M-1

其中：k=0，1，2，…，L-1

式中：

—輸入層第i個節點的輸出值；

—隱藏層第j個節點的輸出值；

—輸入層第i個節點到隱藏層第j個節點的權系數；

—隱藏層第j個節點到輸出層第k個節點的權系數；

—中間層第j個節點的閥值；

—輸出層第k個節點的閥值；

—輸出層中第k個節點的實際輸出值；

城市規模大小與現代有軌電車應用模式一一對應，不同的城市規模對應著不同的有軌電車應用模式，研究現代有軌電車應用模式就需要對城市規模進行宏觀研究，對于現代有軌電車適用性的研究方法很多，本文主要采用BP神經網絡方法對蘭州新區現代有軌電車適用性進行評價，根據蘭州新區現代有軌電車線網規劃可知，要建立蘭州新區現代有軌電車適用性神經網絡模型，按照配置階段、訓練階段和分類階段三層合理確定網絡層數，確定使用三層BP網絡對蘭州新區現代有軌電車適用性進行評價，再根據蘭州新區現代有軌電車的實際情況，有序配置各獨立層神經元數，在大量研究和前人經驗的基礎上，將輸入層節點確定為20個，隱藏層節點確定為15個，神經元輸出確定為1個，建立了20*15*1的BP網絡神經評價模型。

（1）神經網絡輸入論域的確定

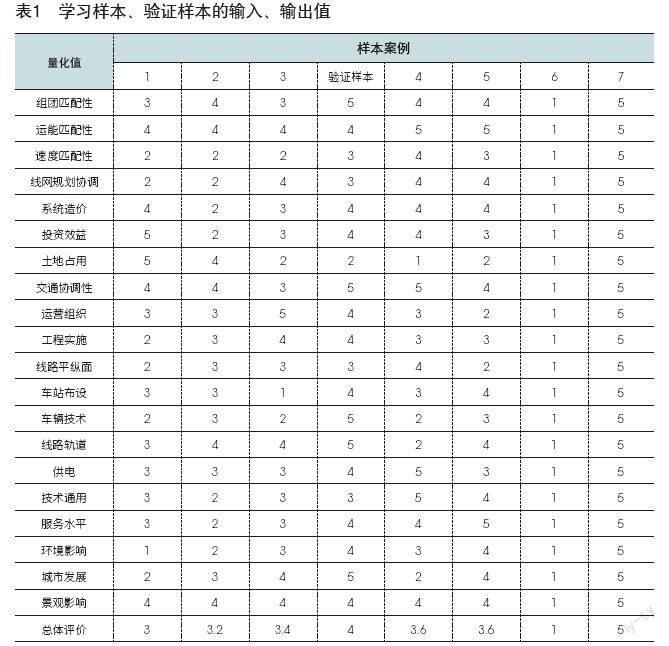
對于已建立的現代有軌電車適用性評價模型，主要從區域適用性評價、系統適用性評價、技術可行性評價、系統社會效益評價四個方面入手，選擇組團匹配性、運能匹配性、速度匹配性、系統造價、線路平縱面、車站布設、線網規劃協調、投資效益、土地占用、與其他設施協調性、運營組織、工程實施、車輛技術、線路軌道、供電、技術通用、服務水平、環境影響、景觀影響、城市發展20個指標作為神經網絡的輸入論域。

（2）樣本值的建立

本文對現代有軌電車適用性的評價分為5個等級，分別為：差，一般，好，較好，很好；對應值分別為1，2，3，4，5；輸出節點的值也對應于此評價結果。

分別選擇英國倫敦、美國波特蘭、法國巴黎、日本東京、中國北京五個城市現代有軌電車的應用模式，分別定義為樣本1、樣本2、樣本3、樣本4和樣本5，澳大利亞墨爾本現代有軌電車的應用模式為驗證樣本，同時確立各輸出值。

同時，根據模型精度需要，確定了連個特殊樣本：樣本6和樣本7。

還有兩個特殊樣本，樣本6和樣本7。

為了方便計算，將所有樣本值進行無量綱化，輸入輸出學習樣本和驗證樣本，可以得到如表1所示的數據。

（3）神經網絡學習

為了克服收斂速度慢，難以確定隱層和隱層的節點數，本文采用自適應lr的梯度下降法，這種算法在訓練過程中能夠合理地改變學習率，合理地避免計算上的缺陷，有利于訓練的穩定性，確保了訓練速度和精度。本文編制Matalab程序來實現神經網絡學習的過程，對蘭州新區現代有軌電車適用性進行評價。BP模式訓練程序如下：

p=[3 4 3 5 4 4 1 5;

4 4 4 4 5 5 1 5;

2 2 2 3 4 3 1 5;

2 2 4 3 4 4 1 5;

4 2 3 4 4 4 1 5;

5 2 3 4 4 3 1 5;

5 4 2 2 1 2 1 5;

4 4 3 5 5 4 1 5;

3 3 5 4 3 2 1 5;

2 3 4 4 3 3 1 5;

2 3 3 3 4 2 1 5;

3 3 1 4 3 4 1 5;

2 3 2 5 2 3 1 5;

3 4 4 5 2 4 1 5;

3 3 3 4 5 3 1 5;

3 2 3 3 5 4 1 5;

3 2 3 4 4 5 1 5;

1 2 3 4 3 4 1 5;

2 3 4 5 2 4 1 5;

4 4 4 4? 4 4 1 5];

net=newff（minmax（p），[15，1]，{'tansig'，'purelin'}，'traingdm'）;? %形成矩陣p，建立隱層15個節點，輸出一個神經元的神經網絡訓練模型

net.trainParam.show=100;? %顯示中間結果的周期為100

net.trainParam.lr=0.05;? ?%學習率為0.05

net.trainParam.mc=0.9;? ? %網絡動量傳遞系數0.09

net.trainParam.epochs=100;? %最大迭代次數100

net.trainParam.goal=1e-10;? ? %訓練進度

t=[3 3.2 3.4 4 3.6 3.6 1 5 ];

net=train（net，p，t）

通過學習訓練，得到神經神經網絡的目標值和輸出值，如表2所示。

（4）模型驗證

取澳大利亞墨爾本現代有軌電車適用模式對上述訓練模型進行驗證，其指標無量綱化的值見表2，將數值輸入模型進行計算，所得到的數據為3.3350，與目標所得值3.6000相比較，誤差很小，模型訓練成功。

save chh_net net

P=[4 4 4 4 4;3 4 4 5 4;4 3 4 4 4;4 4 3 3 3;4 4 4 3 4;4 4 4 2 3;4 3 2 3 3;5 5 5 4 5;4 4 4 4 4;3 4 4 3 4;4 5 4 4 5;3 3 4 3 3;4 4 4 4 4;4 3 4 5 4;4 3 3 4 4;4 5 4 3 4;4 4 4 4 4;3 4 4 3 4;5 4 5 5 4;4 5 4 4 5]? A=sim（net，p）

A =

3.3350

（5）模型的儲存

將上述訓練好的神經網絡模型（20，15，1）存入知識庫中，對其它地區現代有軌電車適用性可以進行評價，只需要輸入評價矩陣即可。

4 蘭州新區適用性量化評價及結論

根據蘭州新區現代有軌電車線網規劃的相關信息可知，對蘭州新區現代有軌電車適用性評價的參數做無量綱化處理，給出五組評價值，見表３：

量化值輸入模型計算，程序如下：

save chh_net net

P=[4 4 4 4 4;3 4 4 5 4;4 3 4 4 4;4 4 3 3 3;4 4 4 3 4;4 4 4 2 3;4 3 2 3 3;5 5 5 4 5;4 4 4 4 4;3 4 4 3 4;4 5 4 4 5;3 3 4 3 3;4 4 4 4 4;4 3 4 5 4;4 3 3 4 4;4 5 4 3 4;4 4 4 4 4;3 4 4 3 4;5 4 5 5 4;4 5 4 4 5];

A=sim（net，p）

A =

3.3350? 3.3344? 3.3240? 3.3198? 3.3350

蘭州新區現代有軌電車適用性評價的結果在好和較好之間，充分說明了蘭州新區建設現代有軌電車是有必要的。

參考文獻：

[1]王艷萍．城市軌道交通線網規劃方案評價方法及應用研究[D]．北京，北京交通大學，2013．

[2]牟潔．城市軌道交通網絡規劃綜合評價[D]．青島，大連理工大學碩士學位論文，2013．

[3]孟祥定．綠色交通視角下城市軌道交通網絡規劃決策方法及應用[D]．湖南，湖南大學，2007．