關(guān)于動圓問題破題方法的舉例探究

李平

【摘? 要】? 動圓問題解析時需要結(jié)合方法策略來轉(zhuǎn)化問題條件、構(gòu)建策略.常用的方法有特殊位置法、分類討論法、化歸轉(zhuǎn)化法，本文結(jié)合實例探究解法，分析破題思路，并總結(jié)構(gòu)建策略，與讀者交流.

【關(guān)鍵詞】? 動圓；分類討論；化動為靜

動圓問題時是初中幾何較為特殊的問題之一，問題常以圓的運動為背景來構(gòu)建幾何綜合，探究學(xué)習(xí)時需要使用一定的方法技巧解析問題，降低思維難度.下面舉例其中常用的三種方法：特殊位置法、分類討論法、化歸轉(zhuǎn)化法.

1? 把握特殊位置，構(gòu)建模型推導(dǎo)

特殊位置分析是解析動圓問題的重要方法，通過分析動圓可到達的特殊位置來確定模型，解析時分兩步構(gòu)建：第一步，分析動圓的移動范圍，結(jié)合問題確定其特殊位置；第二步，把握特殊位置構(gòu)建模型，代入條件分析求解.

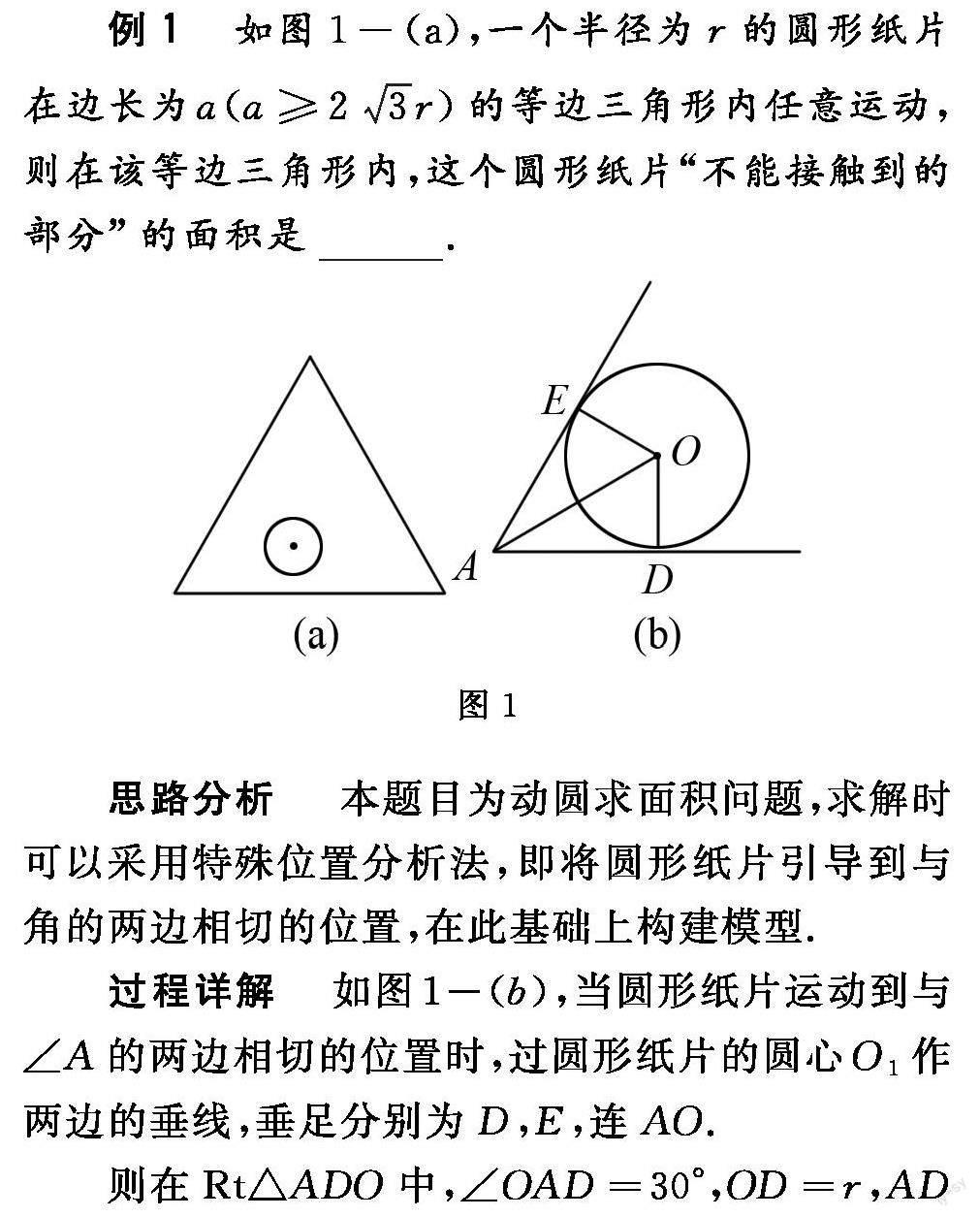
例1? 如圖1-（a），一個半徑為r的圓形紙片在邊長為a（）的等邊三角形內(nèi)任意運動，則在該等邊三角形內(nèi)，這個圓形紙片“不能接觸到的部分”的面積是? ? ? ? ?.

思路分析? 本題目為動圓求面積問題，求解時可以采用特殊位置分析法，即圓形紙片引導(dǎo)到與角的兩邊相切的位置，在此基礎(chǔ)上構(gòu)建模型.

過程詳解? 如圖1-（b），當(dāng)圓形紙片運動到與∠A的兩邊相切的位置時，過圓形紙片的圓心O1作兩邊的垂線，垂足分別為D，E，連AO1.

則在Rt△ADO1中，∠O1AD=30°，O1D=r，AD=，

可求得S△ADO1=，

S四邊形ADO1E＝2S△ADO=.

由題意可知，∠DO1E＝120°，

得S扇形O1DE=，

所以圓形紙片不能接觸到的部分的面積為（-）=（）r2.

解后評析? 上述求解求解動圓面積問題時，采用了特殊位置分析建模法，把握動圓與角相切時的特殊位置，構(gòu)建面積模型分析.特殊位置分析時，需要關(guān)注兩點：一是圓心的移動軌跡；二是圓與幾何線段的相切關(guān)系.

2? 合理分類討論，分別簡化分析

分類討論在幾何探究中十分常用，同樣可以用于動圓綜合題中.解析時需要分三步進行：第一步，解析動圓運動規(guī)律，確定分類標(biāo)準(zhǔn)；第二步，分情形進行模型討論，推導(dǎo)求解；第三步，綜合分析，確定最終結(jié)論.

例2? 如圖2所示，已知正方形ABCD的邊長為8，點M是AB的中點，點P是BC邊上的動點.連接PM，以點P為圓心，PM長為半徑作⊙P.當(dāng)⊙P與正方形ABCD的邊相切時，BP的長為? ? ? ? ?.

思路分析? 本題目為動圓求線段問題，設(shè)定了圓心點P的移動軌跡，求解時需要討論圓與正方形邊相切的情形，在構(gòu)建模型，提取其中直角三角形模型，解析求線段長.

過程詳解? 分兩種情形討論⊙P與正方形邊相切，具體如下.

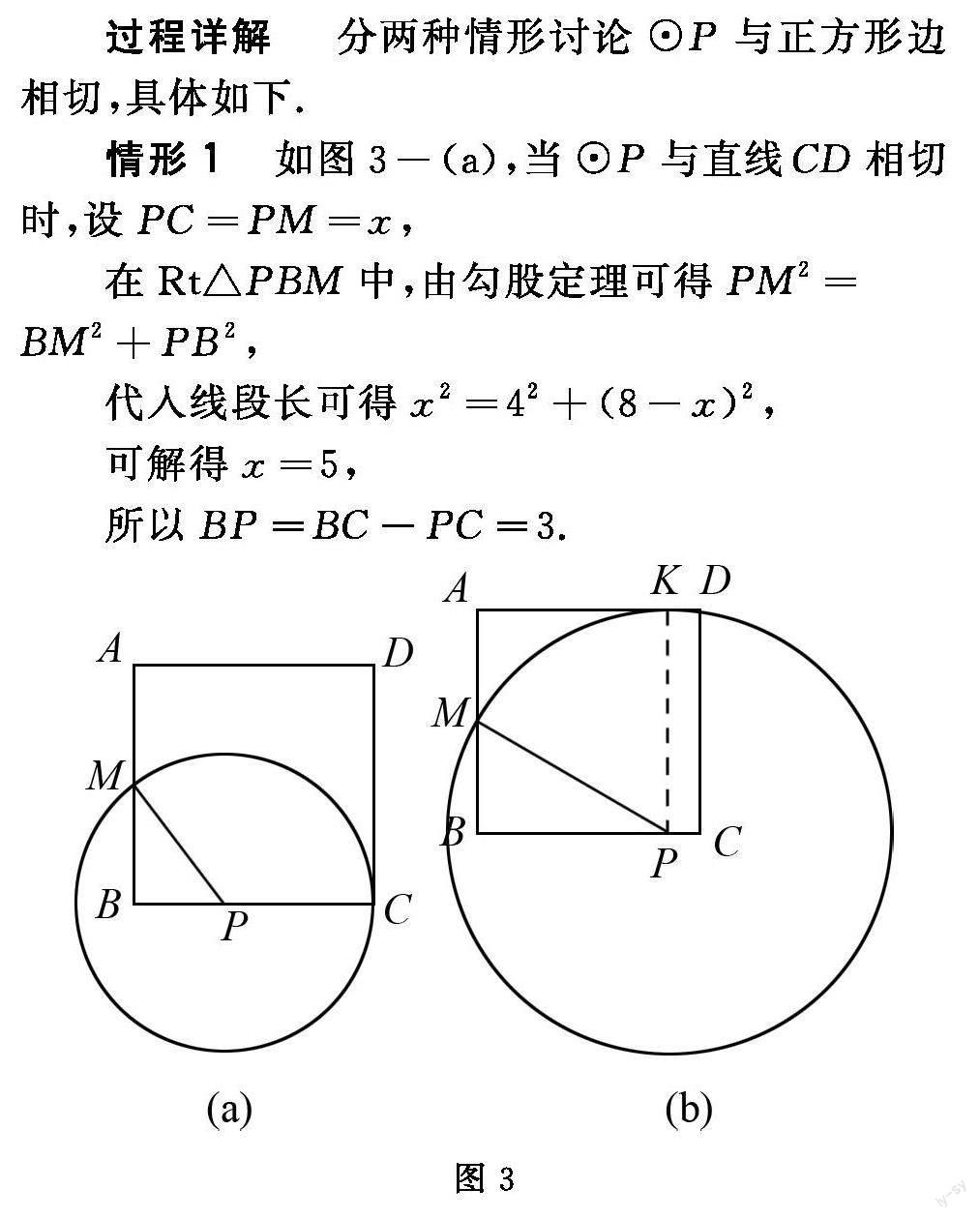
情形1? 如圖3-（a），當(dāng)⊙P與直線CD相切時，設(shè)PC=PM=x，

在Rt△PBM中，由勾股定理可得PM2＝BM2+PB2，

代入線段長可得x2=42+（8﹣x）2，

可解得x＝5，

可推得PC=5，BP=BC﹣PC=3.

情形2? 如圖3-（b），當(dāng)⊙P與直線AD相切時，

設(shè)切點為K，連接PK，則PK⊥AD，四邊形PKDC是矩形.

可推知PM=PK=CD=2BM，

所以BM=4，PM=8.

在Rt△PBM中，由勾股定理可得PB=.

綜上所述，BP的長為3或.

解后評析? 上述動圓問題中，圓心的軌跡確定，求解線段長，需要討論圓與線段的相切情形，故采用分類討論的思維方法可極大降低思維難度.分類討論求解動圓問題時，需要注意兩點：一是慎重確定分類標(biāo)準(zhǔn)，不重復(fù)，不缺漏；二是對于每一種情形，要注意討論是否成立.

3? 幾何化歸轉(zhuǎn)化，化動為靜分析

化歸轉(zhuǎn)化同樣可以用于動態(tài)幾何問題中，求解時需要根據(jù)條件轉(zhuǎn)化為一般的幾何問題，如分析線段長、點位置坐標(biāo)等.具體求解時需要挖掘動圓問題本質(zhì)，根據(jù)條件進行轉(zhuǎn)化，再結(jié)合模型討論分析.

例3? 如圖4-（a）所示，已知正方形ABCD的邊長為8，⊙O的半徑為2.若⊙O在正方形ABCD內(nèi)平移（⊙O可以與該正方形的邊相切）.則點A到⊙O上的點的距離的最大值為? ? ? ? ?.

思路分析? 本題目為動圓求距離問題，求點A到圓上距離的最大值，結(jié)合圓的性質(zhì)，可將其轉(zhuǎn)化為求解點A到點O距離的最大值，顯然需要滿足點O在對角線AC上，后續(xù)再結(jié)合圓相切求解.

過程詳解? 分析可知當(dāng)⊙O與CB、CD相切時，圓心O在斜邊AC上時，

⊙O與AC的交點P到A點的距離最大，如圖4-（b），所示.

過O點作OE⊥CB于E，OF⊥CD于F，

因為CB與CD為⊙O的切線，

則OE=OF=2.AC為正方形的對角線，

O點在AC上，則∠OCE＝45°，

AC=，OC=，

所以PC=OC-OP=，

AP=AC﹣PC=，

即點A到⊙O上的點的距離的最大值為62.

解后評析? 上述求解距離最值時，結(jié)合圓的性質(zhì)將其轉(zhuǎn)化為兩點之間的距離，再結(jié)合共線性質(zhì)求解.整體上采用的是“幾何劃歸轉(zhuǎn)化，化動為靜”分析的思維方法.該方法再使用時分為兩步：第一步，分析問題特征，挖掘問題本質(zhì)，聯(lián)系幾何性質(zhì)定理轉(zhuǎn)化；第二步，分析轉(zhuǎn)化后問題，再構(gòu)建模型求解.

4? 結(jié)語

總之，動圓問題的破解方法較為眾多，上述所呈現(xiàn)是其中較為常見的三種，方法思路構(gòu)建時均涉及到了數(shù)形結(jié)合、模型構(gòu)造的思維方法.探究學(xué)習(xí)時，需要深刻理解方法本質(zhì)，掌握方法精髓及構(gòu)建策略.同時關(guān)注問題類型，結(jié)合問題總結(jié)方法策略.