基于整體觀的等腰三角形單元教學設計

潘麗莎

【摘? 要】? 教師在使用教材時要充分尊重但不能盲從，必要時需對教材內容的編排進行優化設計，以滿足學生的理解及思維發展需求，落實學科素養.等腰三角形單元的課堂教學容易出現內容割裂、銜接不自然、活動安排突兀的問題，為了避免出現知識呈現碎片化、探究操作淺表化的問題，教師就要運用整體觀理解教材的編排思路、尋找邏輯關系，從整個知識體系上把握呈現順序，必要時需對課時內容進行適當調整.

【關鍵詞】? 初中數學；教材優化；課堂教學

1? 問題的提出

近期，筆者連續聽了兩節等腰三角形的軸對稱性第三課時的課堂教學.教材是蘇科版《義務教育課程標準實驗教科書·數學》八年級上冊“2.5等腰三角形的軸對稱性”.經過對教學過程的觀察，發現其教學中存在一些問題.進一步研究發現，教材內容的呈現方式深深地影響著教師的教學行為.經過深入研究，發現對教材中的這部分內容的編排和設計可以做優化和重構.

2? 課例研究

2.1? 兩個課例的教學基本思路

（1）復習回顧，知識再現

提問：上節課我們學習了什么？（如何判斷一個三角形是等腰三角形？）

通過復習，喚起學生的記憶，引出第一個主題：應用判定方法解決問題.

（2）例題示范，變式拓展

教師給出書本第64頁的例題2：

已知：如圖1，∠EAC是△ABC的外角，AD平分∠EAC，AD∥BC．求證：AB＝AC．

首先教師示范分析問題的方法和途徑，并示范證明過程.其次，利用教科書上的思考環節，進行變式教學，追問你能否改變條件或結論，形成新的問題？教師最后歸納.

（3）折紙活動，操作探究

教師按教科書的設計程序要求學生先操作折紙，嘗試把一張直角三角形紙片按圖2—5要求折疊，拋出第二個主題：探究——猜想直角三角形斜邊中線的性質.

（4）演繹推理，歸納性質

教師引導學生將猜想的結論進行分析并證明，簡要寫出過程.兩位教師一個是按照教科書的構造方法加以證明的，即在∠C的內部做∠BCD=∠B，然后證明∠ACD=∠A，此時說明了兩條折痕交于一點的原因，從而歸納出直角三角形斜邊上的中線性質.另一個教師是由折疊得到線段BD=CD，得出∠BCD=∠B，利用等角的余角相等得∠ACD=∠A，從而知道AD=CD.

（5）應用性質，歸納總結

2.2? 課例中存在的問題

（1）知識呈現碎片化

課下與這兩位教師所在的備課組座談交流，他們均表示，這一節課內容不好銜接，第二個教學環節讓學生感到很突然，前面應用等腰三角形的判定解決問題，后面突然繞道直角三角形折紙，不能自然、合理的進行數學思考.他們認為例2的作用僅是等腰三角形判定方法的應用，隨后的變式就是為了歸納一種基本圖形：角等分+平行=等腰三角形.而后半程的直角三角形性質的探索與前面沒有關聯.

（2）操作探索淺表化

課例中的教學第二環節，兩位教師都說：請同學們拿出課前準備的直角三角形紙片，按書本的方法進行折疊.這種淺表化的實驗操作源于教師沒有深入思考為什么這個環節要安排在等腰三角形的判定應用之后？研究直角三角形的斜邊中線性質與等腰三角形的有機聯系是什么？為什么要折疊？為什么要這樣折疊？為什么拿出的是直角三角形紙片？而不是其他斜三角形的形狀？如何銜接？

3? 剖析原因

3.1? 融入整體理解教材

在教師的眼里之所以本節課內容割裂、沒有關聯，其原因之一在于教師.教師沒有從單元的整體結構研究本課時的作用，沒有前后聯系找到合適的呈現順序，更沒有基于學生已有知識經驗自然生成，只是教教材.

《課標》要求：“把每堂課教學的知識置于整體知識的體系中，注重知識的結構和體系處理好局部與整體的關系，引導學生感受數學的整體性”.在實施教學時，教師要處理教材、學生、學習環境幾個要素的關系.備教材應站在整體的高度上理解教材.蘇科版教科書中本單元是以等腰三角形為主題，而等腰三角形的研究又在軸對稱的大體系之下.如果從這種關聯性出發，則需要設計與軸對稱、等腰三角形有關的問題鏈條形成研究路徑，讓學生沿著等腰三角形的研究路徑，自然合理地發現問題，而不是突然地動手折紙、探究.所以教師需要以系統和整體的觀點思考，從軸對稱的視角、依托等腰三角形的性質及判定來籌劃、制定本節課的教學設計.

3.2? 重審教材編排思路

但若深究原因，兩位教師不在同一學校，課前沒有溝通，但教學設計的程序卻相似，出現的問題也是一樣的.那么他們的困惑來源于哪里呢？這要回到教材里找原因.

“教材對教師的教學行為具有重大影響，教材的編寫責任重大，需要不斷研究并改進教材的建設，使之能承擔起引領教師的數學教學，促進數學教學發展現實的核心素養，落實數學育人的使命.”對于等腰三角形的軸對稱性，不同版本的教材都是放在軸對稱的體系下，體現了應用軸對稱來研究新問題的編寫意圖.而直角三角形斜邊上的中線性質有的版本是在等腰三角形單元里研究（蘇科版），有的版本放在特殊的平行四邊形之后學習（人教版、北師大版），有的版本是將直角三角形自成單元研究（滬教版、浙教版）.按《課標》要求，直角三角形斜邊上的中線性質是放在全等和軸對稱圖形的研究的后面，明確運用全等、等腰三角形知識探索并證明這個性質.不同版本教材對于直角三角形的性質探索方式基本有兩種：一種是直接給出定理內容，讓學生加以證明；另一種是設計操作性研究，體現定理的探索過程.無論哪一種呈現方式，證明的思路都是利用構造全等圖形、構造角的轉化思想，與等腰三角形并無緊密、直接關系.這是造成教師邏輯鏈斷裂的原因，所以不能自然合理的探索直角三角形斜邊上的中線性質.

4? 對本單元內容設計的改進建議

4.1? 反思編排順序

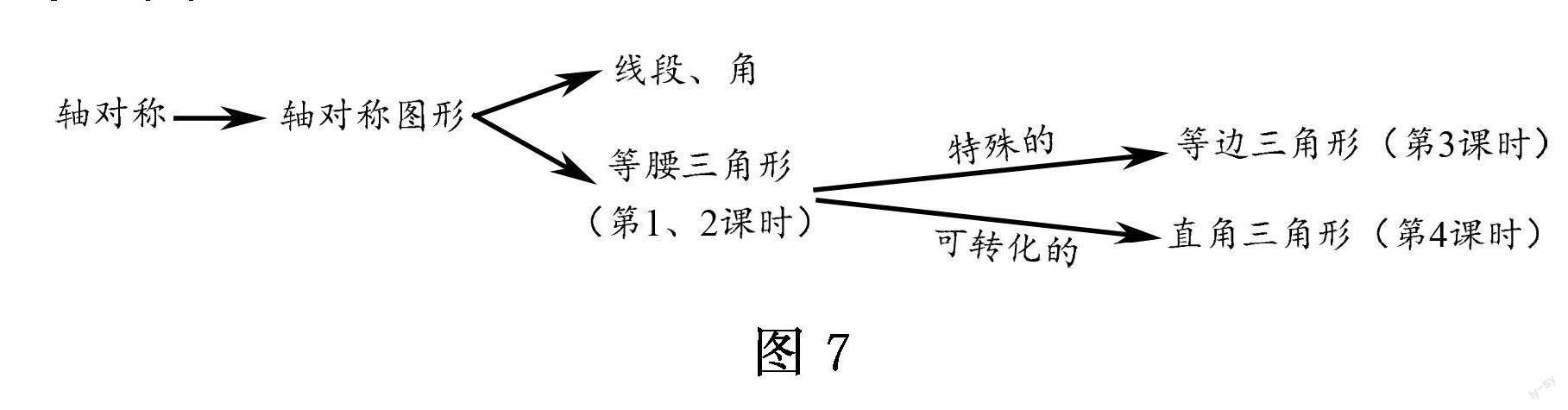
重新審視本單元的教材，可以調整編排順序：第三課時的例2可以前置于第二課時的等腰三角形的判定里學習，原第二課時里的等邊三角形是特殊的等腰三角形，可以作為更特殊的軸對稱圖形放在第三課時學習研究，原第三課時的直角三角形性質作為可轉化成軸對稱圖形的特殊圖形去探究.即第一課時等腰三角形性質及應用探究，第二課時等腰三角形判定方法探究，第三課時等邊三角形探究，第四課時直角三角形探究.

4.2? 基于整體觀的設計

站在軸對稱知識的體系中，作為等腰三角形研究的自然延伸，運用數學實驗研究方法，對于直角三角形探究設計建議如下.

課題? 直角三角形探究

課前準備? 如圖6中的等腰三角形紙片、直角三角形紙片各一張、斜三角形紙片兩張.

問題設計：

（1）拿出一張等腰三角形紙片①，將其翻過來，仍舊和原圖形重合；為什么？

（2）拿出一張其他三角形紙片②③④，將其翻過來，與原圖形重合嗎？為什么？能否把它們進行分割再翻過來與原圖形重合？

思考下面的問題：

（3）能否剪一刀，將紙片②③④剪成兩個三角形，其中一個是等腰三角形？

（4）在第3問的基礎上，觀察另一個三角形的形狀.說出你的發現.

（5）比較同組其他同學，你們的發現一樣嗎？

（6）紙片②③有沒有這種特殊性？請討論研究“所有的直角三角形都能有這種特性”嗎？為什么只有直角三角形可以？

（7）回顧剪紙過程，將剪開的三角形再拼合成原圖形直角三角形紙片④，觀察分割線的特點并思考，能證明另一個三角形的形狀嗎？引導學生在練習本上畫圖，獨立思考、證明.繼而歸納性質.

（8）經過證明剪出的兩個三角形都是什么形狀？此時的紙片④，經過分割，再把每一部分翻過來可以與原圖形重合嗎？

（9）思考：紙片②③能否經過分割，再把每一部分翻過來，與原圖形重合嗎？學生再次動手操作.

（10）如果給你一張任意四邊形紙片呢？學生嘗試實驗，展示方法.

5? 結語

通過上述探究過程，把直角三角形斜邊上的中線性質的發現、提出、證明過程融合到軸對稱的框架下的等腰三角形的深化研究活動中，體現了探索三角形形狀就要研究其構成的要素的數量關系.這樣，既可以讓學生經歷自然合理的觀察、動手、發現、歸納的抽象過程，又是幾何圖形研究的一般路徑的再現，有利于發展學生的數學探究意識、積累思考活動經驗.

【本文是江蘇省中小學教學研究課題2021年度第十四期重點課題《初中生數學建模素養培育實踐研究》（2021JY14-ZB83）階段性研究成果之一】

參考文獻：

［1］中華人民共和國教育部.義務教育數學課程標準（2011年版）［S］.北京：北京師范大學出版社，2012.

［2］吳增生.三角形中位線定理教材設計之我見［J］.中國數學教育（初中版），2018（23）：3-5+10.

［3］章建躍.從整體上把握好教學內容［J］.中小學數學（高中版），2010.3.封底.

［4］王紅權 李馨.從系統的觀點看一元二次方程的解法教學設計［J］.數學教育學報，2019，28（03）.94-97.