高維具有間接信號生成的趨化模型解的有界性

張 云,辛 巧,2

(1.伊犁師范大學數學與統計學院,新疆 伊寧 835000;2.伊犁師范大學應用數學研究所,新疆 伊寧 835000)

0 引言

由KELLER和SEGEL[1]于1970年提出的Keller-Segel模型(簡稱經典的K-S模型)是經典的生物趨化性模型之一,經典的K-S模型描述了細菌團在趨化吸引下的聚合行為.目前,經典的K-S模型已受到國內外學者的廣泛關注,關于解的存在性、有界性、爆破行為、漸近行為以及弱解已取得了一系列研究成果[2-8].在此基礎上,由于許多趨化模型的化學信號不能直接由細胞自身直接產生,因此對于經典的K-S模型,具有間接信號以及Logistic源的研究是有意義的,如STROHM等[9]提出了一個北美物種山地松甲蟲通過啃食樹體的方式破壞生態平衡,山地松甲蟲會在樹上筑巢產卵分泌信息素以吸引飛行的山地松甲蟲,但飛行中的山地松甲蟲不會直接釋放信息素,從而許多數學工作者考慮如下具有間接信號生成且帶有Logistic源的趨化模型:

(1)

假設D(u)=(u+1)-α,S(u)=u(u+1)β-1,且f(u)=μu-μu2,其中α,β∈.對于f(u)=μu-μu2的情況,當N=3,D(u)=1,S(u)=u時, HU和TAO[10]證明了模型(1)的唯一經典解是一致有界的.同時,若則當t→∞時該模型的解在L∞(Ω)的范數下收斂于平衡點

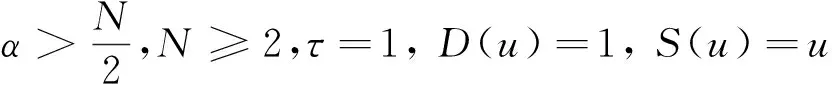
受以上研究結果的啟發,本文討論具有間接信號生成以及Logistic源的生物趨化模型:

(2)

(3)

本文的主要結果如下:

定理1當N=4,δ>τ時,且模型(2)的初值(u0,v0,w0)滿足(3)式,且非負函數u,v和w在Ω×(0,∞)上有界,則對任意的t>0,存在常數C>0,使得

‖u(·,t)‖L∞(Ω)+‖v(·,t)‖W1,∞(Ω)+‖w(·,t)‖L∞(Ω)≤C,

(4)

1 預備知識

引理1 假設非負函數u0,v0和w0滿足式(3),則存在Tmax∈(0,∞]和非負函數(u,v,w)滿足:

(5)

進一步地,若Tmax<+∞,則當t→Tmax時,有

‖u(·,t)‖L∞(Ω)+‖v(·,t)‖W1,∞(Ω)+‖w(·,t)‖L∞(Ω)→+∞.

(6)

根據以上存在性理論,對任意的s∈(0,Tmax),有

(7)

因此,不失一般性,假設存在C>0,使得

(8)

引理2 存在正常數C1>0,滿足式(2)和式(3),使得對任意的t∈(0,Tmax),有

(9)

引理3 假設

(10)

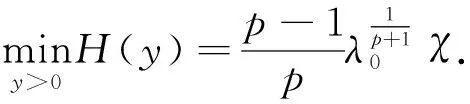
2 趨化模型解的有界性估計

(11)

(12)

其中,ε是充分小的正數.

證明 設

根據文獻[14],可以得到

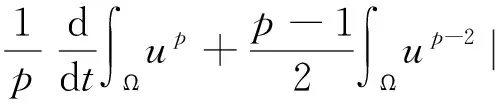
(13)

為了估計式(13)右邊第一項,借助Young不等式,對于任意的t∈(0,Tmax),有

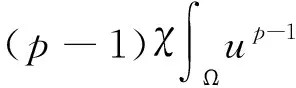
設

(14)

其中,ρ0的定義見(9)式.

由式(14),結合Young不等式,對于任意的t∈(0,Tmax),有

(15)

將(15)代入式(13),對于任意的t∈(0,Tmax),可得

(16)

對于任意的t∈(0,Tmax),且對(16)結合常數變易法,有

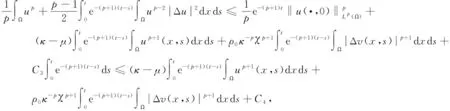
(17)

其中,

除此之外,對于任意的t∈(0,Tmax),有

(18)

接下來,在模型(2)的第三個方程的兩邊同乘wp,并在Ω上積分,對于任意的s∈(0,Tmax),δ,τ>0,存在正數C5>0,使得

則

(19)

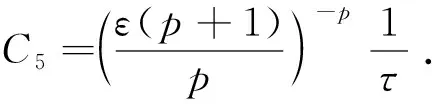
對于任意的s∈(0,Tmax),對式(19)運用常數變易法,有

為了方便計算,設

根據Fubini定理,可得

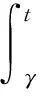
當C7<0,有

(20)

將式(20)代入式(18),有

(21)

接下來,將式(21)代入式(17),結合引理3,可得

其中,

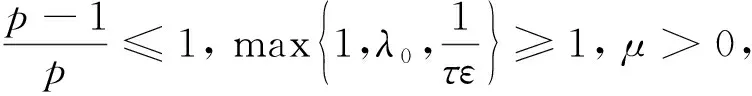
因此引理4得證.

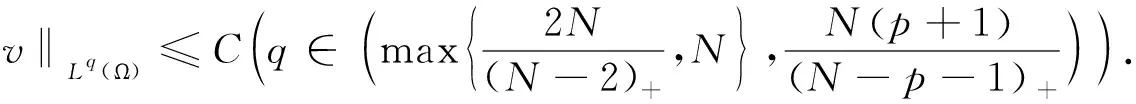
基于之前的估計,對于任意的l>N,可以得到‖u(·,t)‖Ll(Ω)的有界性.

引理5的證明過程可參見文獻[14].

定理1的證明結合以上引理4和引理5,首先根據‖u‖Lp(Ω)先驗估計,與‖w‖Lp+1(Ω)估計進行耦合,結合常數變易法以及拋物正則性理論,得到了在適當參數的范圍內,‖u‖Lp(Ω)和‖w‖Lp+1(Ω)是有界的,再結合引理1,可得模型(2)的全局經典解是有界的,從而完成了定理1的證明.

3 結語

本文研究了具有間接信號生成且帶有Logistic源的生物趨化模型的解的全局有界性,通過進行適當的先驗估計,并利用常數變易法證明了該模型經典解在適當參數范圍內是全局存在且唯一的,得到了高維情形下該模型的全局經典解是有界的．