無序多分類資料統計分析方法的選擇及在SPSS上的實現
張蓼紅,馮孟潛,包國章,張曉君,白春艷,丁雪梅
(1.吉林大學組織部,吉林 長春 130012;2.吉林大學中日聯誼醫院,吉林 長春 130033;3.吉林大學新能源與環境學院,吉林 長春 130012;4.吉林大學教務處,吉林 長春 130012;5.吉林大學動物科學學院,吉林 長春 130062)
在自然科學和社會科學研究中,經常需要對無序多分類資料進行統計分析。例如,研究患某病仔兔的一個基因(3個基因型)和另一個基因(3個基因型)的分布情況,以及豌豆遺傳性狀實驗中研究豌豆桿的3個性狀和果實的3個性狀的對應關系。再如,通過問卷調查,研究不同社區和不同性別居民獲取健康知識途徑(傳統大眾媒介、網絡、社區宣傳)是否相同,或者研究不同學習階段的學生(本科生、碩士研究生、博士研究生)學習黨的二十大報告內容更喜歡的學習方式(自學、專家作報告、小組學習)等。對于無序多分類資料的統計分析,要考慮變量的數量、分析目的、統計分析方法的前提條件等。如何快速、準確地選擇正確的統計分析方法、如何在SPSS上實現統計分析以及如何解讀SPSS輸出結果,本研究選取典型案例,對上述問題進行逐一解答。
1 基于無序多分類資料的常用的統計分析方法
通過簡單易懂的典型案例分析和流程圖,厘清和展示針對無序多分類資料的常用的統計分析方法的選擇思路。
1.1 典型案例分析
1.1.1 案例描述
為了提高大學生學習營養健康知識的學習效果,對3個學院(動物科學學院、動物醫學學院、植物科學學院)的大學生偏好的學習方式(自學、小組、上課)進行問卷調查,結果見表1。

表1 三種學習方式在不同學院和不同性別學生中的分布情況
問題1:針對大學生偏好的學習方式進行對應分析。
問題2:不同學院的大學生偏好的學習方式構成比有沒有差異?學院和學生偏好的學習方式之間是否有關聯?
問題3:分析學院和性別對學生學習方式偏好的影響。
1.1.2 思路分析
問題1涉及2個變量,行變量“學院”有3個水平,列變量“學生偏好的學習方式”有3個水平。行變量和列變量均為無序多分類資料,研究2個變量之間的對應關系,可以采用簡單對應分析。
問題2要求比較三個樣本構成比之間的差異,可以采用χ2檢驗;研究2個無序多分類資料的變量之間是否有關聯,可以采用關聯性檢驗。
問題3涉及3個變量,其中原因變量有2個,為“學院”和“性別”;結果變量有1個,為“學生偏好的學習方式”。若要分析2個原因變量對結果變量的影響以及影響程度,可采用無序多分類Logistic回歸分析。
1.2 統計分析方法選擇流程
無序多分類資料統計分析方法選擇的流程圖,如圖1和圖2所示,其中R和C分別表示行數和列數,且都大于等于3。
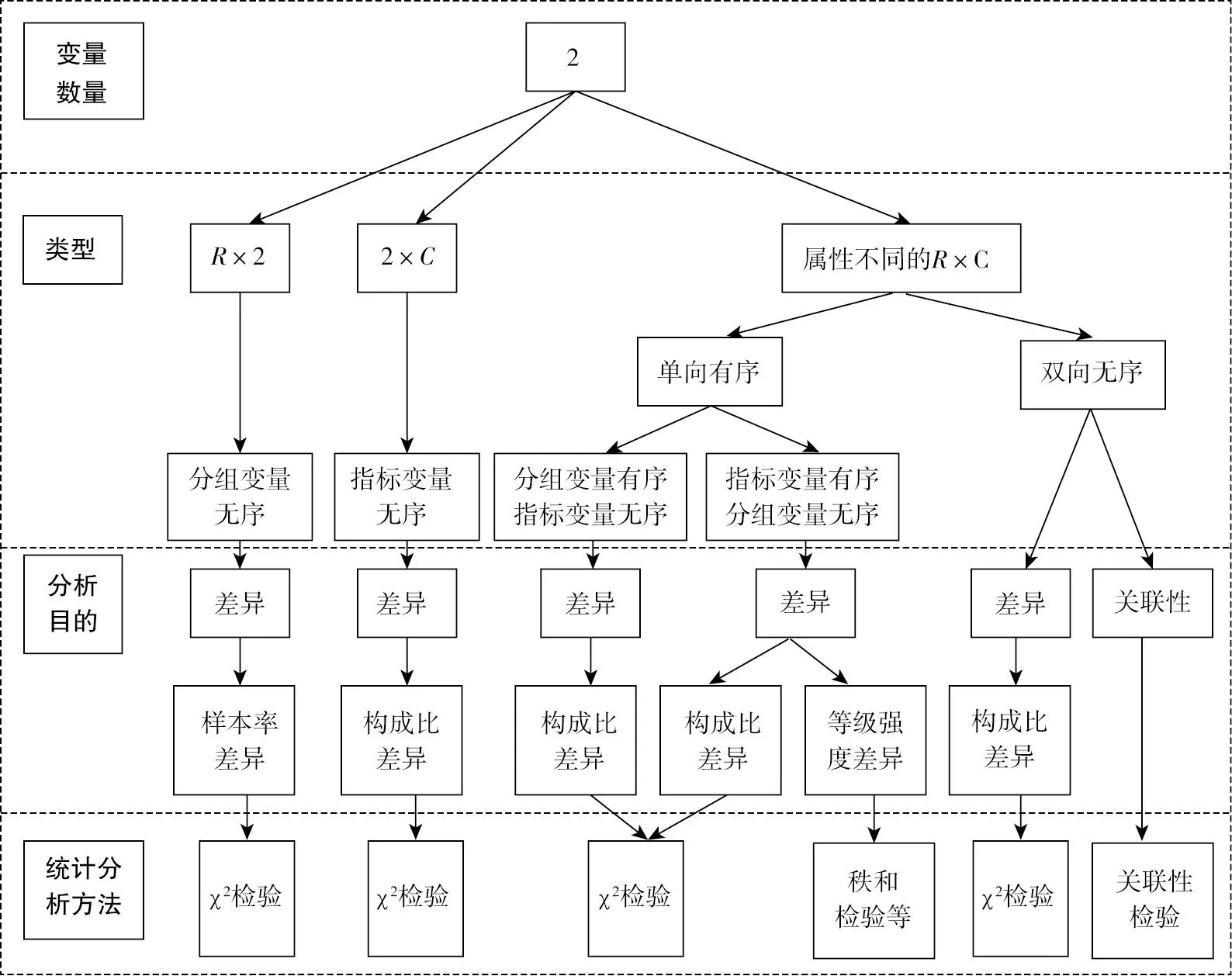
圖1 基于無序多分類資料的R×2、2×C、屬性不同的R×C型常用的統計分析方法選擇的流程圖
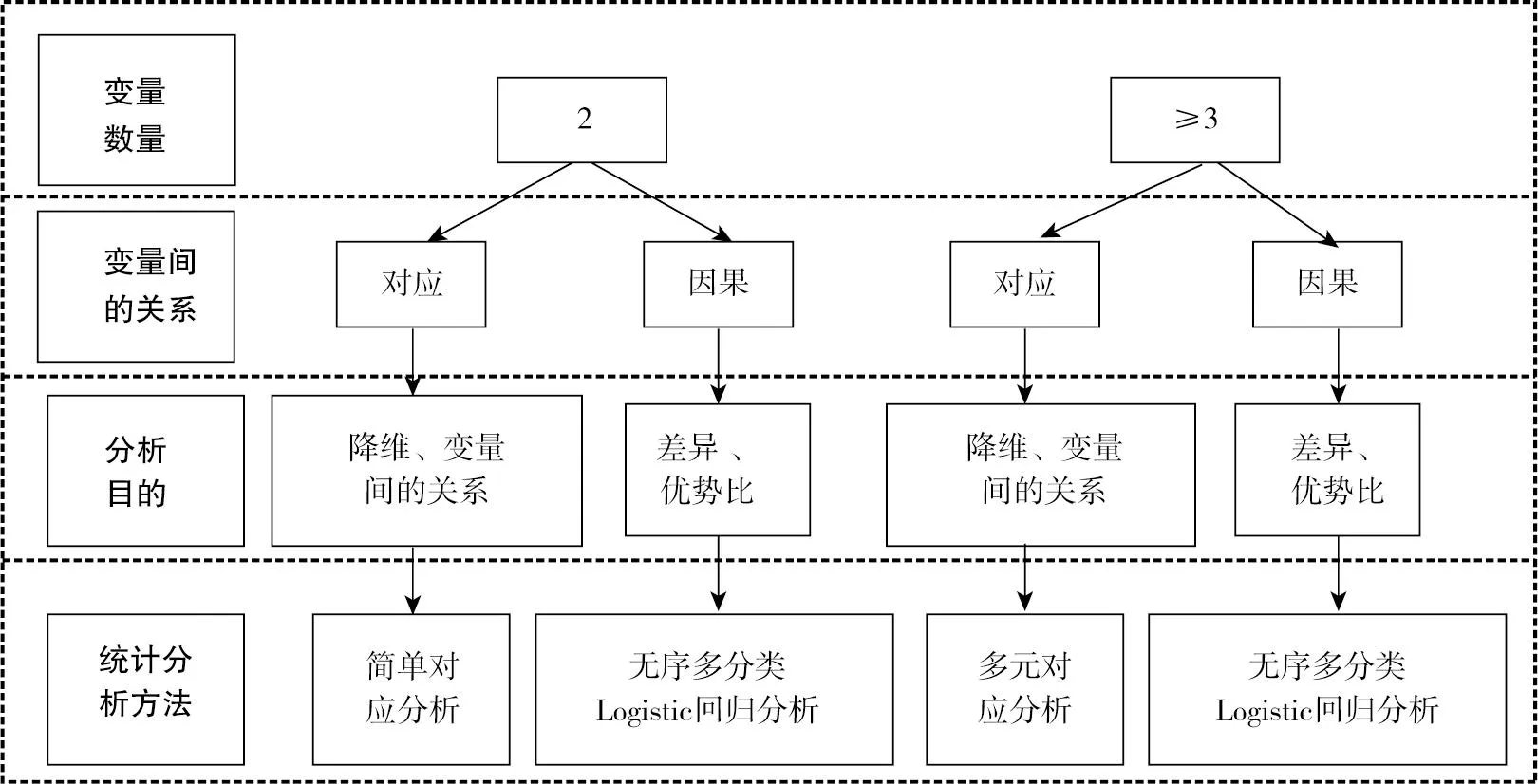
圖2 基于無序多分類資料的常用的多元統計分析方法選擇的流程圖
2 基于無序多分類資料的常用的統計分析方法在SPSS 19.0上的實現
2.1 簡單對應分析在SPSS 19.0上的實現
(1)簡單對應分析實現步驟。①數據錄入和數據加權。數據錄入時,在“變量視圖”中為行變量“學院”和列變量“大學生偏好的學習方式”每個水平賦值(動物醫學、植物科學、動物科學分別賦值為1、2、3;自學、小組、上課分別賦值為1、2、3)。加權步驟:數據→加權個案,加權個案(W)→頻率變量(F):頻數→確定。②簡單對應分析。分析→降維→對應分析,學院→行,定義范圍(最小值為1,最大值為3)→更新→繼續;偏好的學習方式→列,定義范圍(最小值為1,最大值為3)→更新→繼續→確定。
(2)結果解讀。針對問題1的對應分析結果見表2。第一維慣量值為0.038,第二維慣量值為0.003,其相對應的百分比分別解釋了總信息量的93.1%和6.9%,前兩個維度累計解釋了總信息量的100%,即二維圖形可以完全表示兩變量間的信息,并且觀察時以第一維度為主。列聯表行列獨立性的χ2檢驗結果為χ2=29.981,P=0.000<0.01,表明列聯表的行列之間有較強的相關性。

表2 對應分析結果匯總表
對應分析圖(圖3)表明,維度1區分度好,維度2區分度差,動物醫學學院、植物科學學院、動物科學學院的大學生分別傾向于選擇上課、自學、小組學習的學習方式。
2.2 χ2檢驗和關聯性檢驗在SPSS 19.0上的實現
(1)χ2檢驗和關聯性檢驗步驟。①數據錄入和數據加權。數據錄入形式和加權步驟同“2.1”。②χ2檢驗和關聯性檢驗。分析→描述統計→交叉表,學院→行,偏好的學習方式→列,統計量→卡方,相依系數→繼續;單元格→觀察值,期望值,行→繼續→確定。
(2)結果解讀。根據n(總數)和T(理論頻數)的大小選擇P值[1]。χ2檢驗(表3)的結果表明,χ2=29.981,n=741,最小期望計數為51.65,P=0.000<0.01,即3個學院學生偏好的學習方式構成比有極顯著差異。進一步對每2個學院之間的學生偏好的學習方式構成比作差異性比較,χ2檢驗的結果表明,動物醫學學院和植物科學學院,χ2=19.322,n=533,最小期望計數為59.05,P=0.000<0.01,即2個學院學生偏好的學習方式構成比有極顯著差異;動物醫學學院和動物科學學院,χ2=23.622,n=483,最小期望計數為45.22,P=0.000<0.01,即2個學院學生偏好的學習方式構成比有極顯著差異;植物科學學院和動物科學學院,χ2=2.561,n=466,最小期望計數為56.69,P=0.278>0.05,即2個學院學生偏好的學習方式構成比沒有差異。
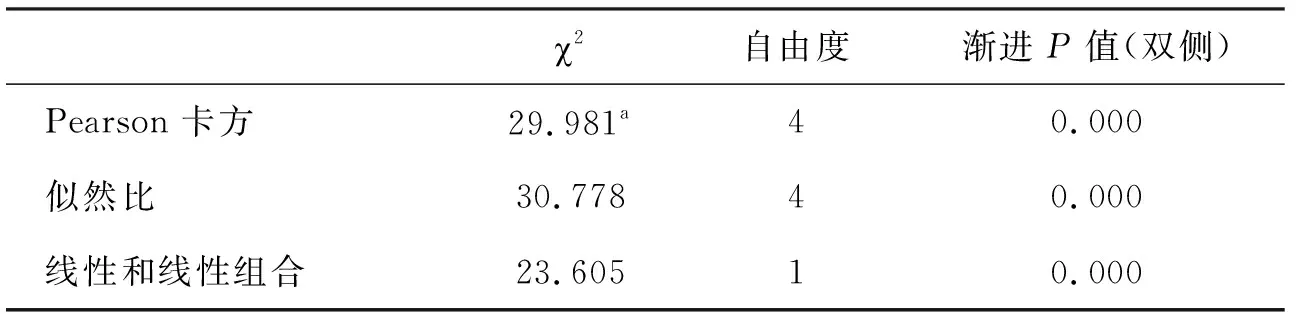
表3 χ2檢驗結果
對稱度量表中關聯性檢驗結果表明,P=0.000<0.05,Pearson列聯系數為0.197,表明學院和學生偏好的學習方式之間有一定關聯。
2.3 無序多分類Logistic回歸分析在SPSS 19.0上的實現
(1)無序多分類Logistic回歸分析步驟。①數據錄入和數據加權。數據錄入時,在“變量視圖”中為自變量“學院”“性別”和因變量“學生偏好的學習方式”的每個水平賦值(動物醫學、植物科學、動物科學分別賦值為1、2、3;男生、女生分別賦值為1、2;自學、小組、上課分別賦值為1、2、3)。加權步驟同2.1。②無序多分類Logistic回歸分析。分析→回歸→多項Logistic回歸,偏好的學習方式→因變量,學院、性別→因子→確定。
(2)結果解讀。模型擬合(表4)的結果表明,似然比卡方檢驗結果P=0.000<0.01,說明至少有一個自變量系數不為0,模型有意義。似然比檢驗(表5)的結果表明,學院似然比檢驗結果P=0.000<0.01,性別似然比檢驗結果P=0.000<0.01,表明學院和性別對模型的作用都有統計學意義。參數估計(表6)的結果表明(動物科學學院和女生為參照,因此其參數默認為0,無法估計),自學與上課兩種學習方式相比,動物醫學學院的學生比動物科學學院的學生更傾向于選擇上課的學習方式(χ2=19.147,P=0.000<0.01,優勢比OR值為0.348),而植物科學學院與動物科學學院的學生的選擇沒有差別(χ2=0.316,P=0.574>0.05);男生比女生更傾向于選擇自學的學習方式(χ2=7.205,P=0.007<0.01,優勢比OR值為1.647,置信區間為[1.144, 2.370],置信區間不包括1)。小組學習與上課兩種學習方式相比,動物醫學學院的學生比動物科學學院的學生更傾向于選擇上課的學習方式(χ2=8.966,P=0.003<0.01,優勢比OR值為0.512),而植物科學學院與動物科學學院的學生的選擇沒有差別(χ2=2.829,P=0.093>0.05);男生比女生更傾向于選擇小組學習的學習方式(χ2=10.526,P=0.001<0.01,優勢比OR值為1.804,置信區間為[1.263,2.576],置信區間不包括1)。由此得出兩個廣義Logit模型:

表4 模型擬合信息

表5 似然比檢驗
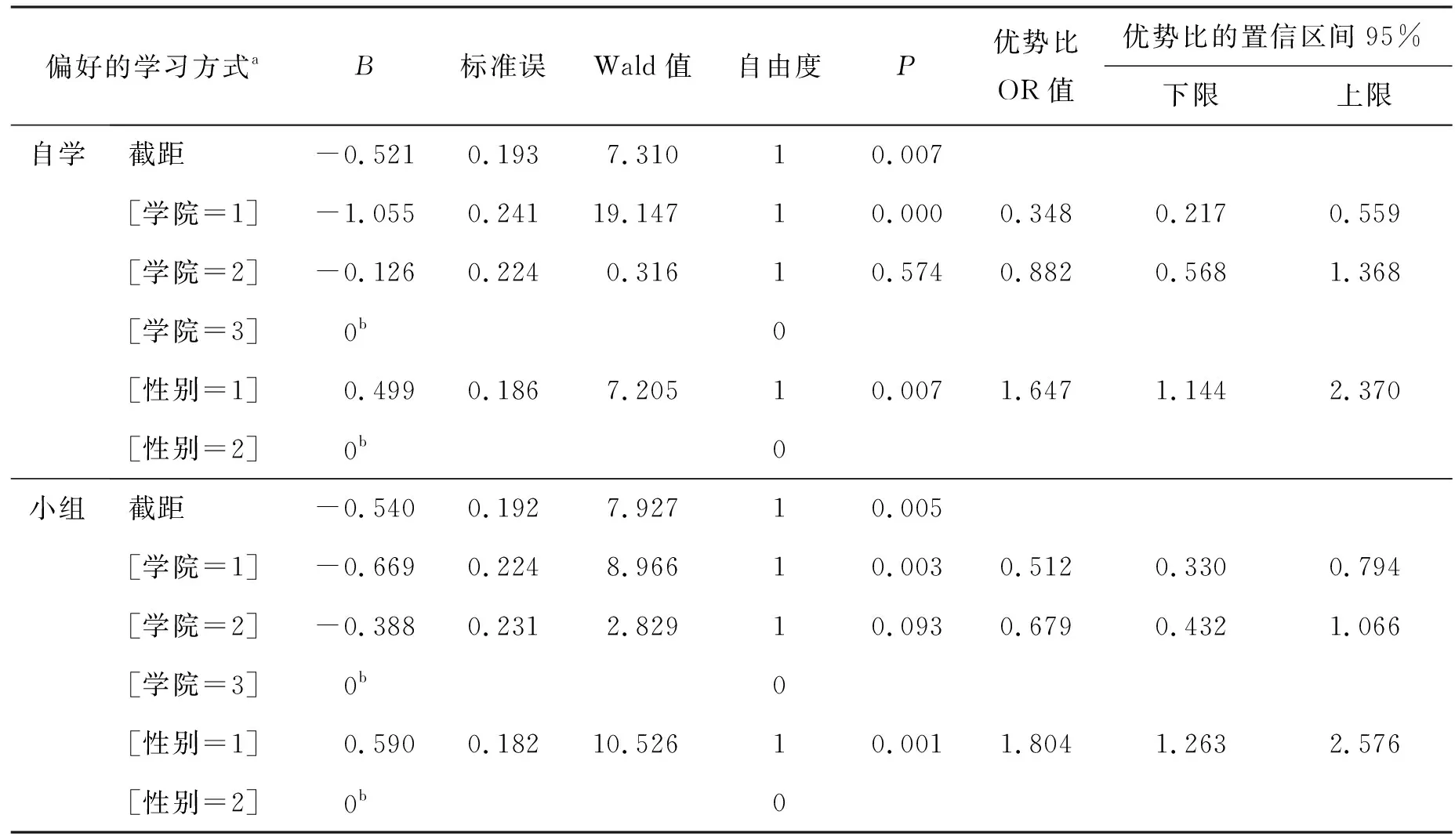
表6 參數估計
其中,X1指動物醫學學院;X2指植物科學學院;X3指男性;ps指各變量組合選擇自學學習方式的概率;pc指各變量組合選擇上課學習方式的概率;pt指各變量組合選擇小組學習方式的概率。
表5中,χ2統計量是最終模型與簡化后模型之間在-2倍對數似然值中的差值。通過從最終模型中省略效應而形成簡化后的模型。零假設就是該效應的所有參數均為0。
3 結語
對于經常出現在R×2、2×C、屬性不同的R×C二維列聯表中的無序多分類資料,χ2檢驗可以進行兩個或多個樣本率或構成比之間的差異比較,如果R×2或不同屬性的R×C類型之間樣本率或構成比有顯著差異,還要利用χ2檢驗進一步對每兩個行變量做進一步差異比較。χ2檢驗的前提條件是:通常各格的理論頻數不應小于1,且1≤T≤5的格子數不宜超過格子總數的1/5[2]。對于不同屬性的R×C類型,如果是雙向無序多分類資料還可以進行關聯性檢驗。χ2檢驗只能進行兩個或多個樣本率或構成比之間的差異比較,不能夠進行等級強度的差異比較;如果對分組變量無序、指標變量有序的單向無序的屬性不同的R×C類型進行等級強度差異的比較,例如比較三種藥物的治療效果(顯效、好轉、無效),須采用秩和檢驗或Ridit分析或有序Logistic回歸分析,其中非參數檢驗方法秩和檢驗和Ridit分析兩種統計分析方法結果是等價的,不受總體分布限制,適用面廣,但不能充分利用信息,檢驗效能低[3-4]。
無序多分類資料的多元統計分析中,常用對應分析和無序多分類Logistic回歸分析。其中,對應分析利用降維思維,以二維效應圖簡潔、直觀地揭示屬性變量之間以及屬性變量各種狀態之間的相互關系[5]。針對兩個變量的簡單對應分析是通過SPSS軟件的“降維”下的“對應分析”子模塊來完成,三個或者三個以上變量則需要通過“最優尺度”子模塊來完成多元對應分析(多重對應分析)。變量個數越多,各個變量的類別取值越多時,對應分析的優勢就越明顯[6]。簡單對應分析能夠輸出對應分析圖,無序多分類Logistic回歸分析能夠獲得優勢比(OR值)以及回歸方程。無序多分類Logistic回歸分析,要求因變量必須是無序多分類資料(自變量資料類型不限),對樣本量也有較高的要求,變量的個數愈多需要的例數相應也愈大,樣本至少大于100,大于500比較合適,一般每一個自變量至少需要10例結局[7-9]。本研究案例中,利用SPSS軟件進行無序多分類Logistic回歸分析時,無序多分類變量“學院”、二分類變量“性別”,這2個變量都進入到“因子”中,如果再增加一個因素:不同學習階段學生(本科生、碩士生、博士生),則此有序變量也要進入到“因子”中,但如果增加的因素是年齡,則此連續變量就要進入到“協變量”中。進行無序多分類Logistic回歸分析,SPSS軟件默認因變量的水平中賦值最高即最后一個作為參考類別,也可以手動設置參考類別,為了方便,最關心哪個水平就賦值最高、選擇系統默認即可。此外,無序多分類Logistic回歸分析還可以考察因素之間的交互作用,只需在點擊“模型”模塊時,將系統默認的“主效應”改為“全因子”,或者選擇“設定/步進式”,將要考察交互作用的因素選入。

