基于多信息融合與GRU的軸承剩余壽命預測

曹勝博，徐彥偉，2，頡潭成，2，王瀏洋

(1.河南科技大學機電工程學院，河南洛陽 471003；2.智能數控裝備河南省工程實驗室，河南洛陽 471003)

0 前言

地鐵牽引電機軸承作為整個地鐵動力系統的關鍵零件，其性能的好壞直接影響地鐵動力系統能否正常運行。在實際工作中，地鐵需要頻繁地啟動停止，地鐵牽引電機軸承需要頻繁承受載荷和轉速的變化，使得軸承容易產生內外圈裂紋、滾動體點蝕等故障[1]。牽引電機軸承一旦出現故障，極易造成重大經濟損失及人員傷亡。如果使用一定的方法計算出地鐵牽引電機的剩余壽命，及時發現早期故障并對設備進行維護，地鐵發生重大事故的風險將大大降低。

傳統的滾動軸承剩余壽命預測方法主要通過模擬機制構建數學模型進行[2]。但在實際應用中，軸承的工作環境復雜，退化過程具有隨機性，難以建立準確的機制模型。基于數據驅動的壽命方法不需要建立繁雜的數學機制模型，并且能夠有效利用各種算法挖掘數據中的隱藏特征，建立軸承的性能退化模型，預測軸承壽命，逐漸成為研究的熱點[3-5]。隨著計算機技術的不斷發展，越來越多的研究人員使用深度學習技術建立軸承退化模型，進行軸承壽命預測方面的研究[6]。在采集軸承的振動信號時，往往包含其他零部件間的噪聲。如何對采集到的信號進行處理，是軸承剩余壽命預測的重中之重。唐旭等人[7]從多元時間序列中提取時域特征數據導入神經網絡，進行剩余壽命預測。趙德尊等[8]研究了基于自適應廣義解調變換的滾動軸承時變非平穩故障特征的提取方法。卷積神經網絡作為深度學習中一種常用的網絡模型，常被用于挖掘數據的深度特征。楊宇等人[9]提出一種動態自學習深度置信網絡，可以從原始信號中提取退化特征，不但縮短訓練神經網絡的時間，同時提高了模型預測準確度。王玉靜等[10]使用一維卷積神經網絡直接對原始一維振動信號進行特征提取。周揚將采集到的未經處理的一維振動信號轉化為二維灰度圖，之后將灰度圖導入卷積神經網絡中進行故障識別，取得了良好的效果[10]。

在壽命預測方面，深度學習技術也展現了強大的非線性擬合能力。張世巖等[11]提出一種結合時間序列數據擴增和雙向長短時神經網絡的軸承壽命預測方法，通過對采集到的時間序列數據進行擴增，分析軸承實際工作過程中的退化規律，旨在提高軸承壽命預測的精度。臧傳濤等[12]在長短時記憶神經網絡的基礎上，使用黏菌算法優化參數，取得了良好的預測效果。

上述方法大多只采集單一振動信號作為數據處理的素材，而振動信號在實際采集過程中極易受到軸承工作環境的干擾。為解決這一問題，本文作者提出一種基于信息融合的門控單元神經網絡預測模型。該模型使用聲發射信號和振動信號融合后的信號作為輸入，能有效彌補單通道數據易受干擾的不足，然后使用GRU神經網絡對壽命進行預測。

1 相關理論

1.1 一維卷積神經網絡

卷積神經網絡根據輸入維度的不同可以分為：一維卷積、二維卷積、三維卷積等。其中提取一維信號數據時，一維卷積神經網絡在特征提取時表現出良好的效果。單層的卷積神經網絡由2個主要部分組成：卷積層和池化層。CNN提取特征的主要步驟為：(1)輸入的一維數據被卷積核依次遍歷，挖掘出深度特征信息；(2)池化層對這些信息進行壓縮降維，選取其中更具有代表性的數據；(3)進行過卷積，池化后產生的新數據序列作為輸入，進行下一次卷積和池化，直到得到想要的數據。下面是具體的運算過程。

(1)卷積層。卷積層的任務是提取出數據中包含的退化信息。根據設計的卷積核的大小，得到不同的特征值。其具體步驟為：卷積核在一維數據上掃描，每移動到一個新的位置，便對該位置的數據進行加權求和，依次進行，直到遍歷完整個數據。提取的數據長度受到卷積核的影響。可以通過設置卷積核的個數、大小、步長等參數調整提取出的特征值。卷積的計算公式如下：

(1)

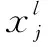
(2)池化層。由于卷積得到的數據量大，含有冗余，因此需要輸入池化層中進行降維處理。池化操作可以有效降低計算量，并減少模型過擬合的概率。池化函數有多種選擇，例如平均池化、L2-范數池化、最大值池化等。其計算公式如下：

(2)

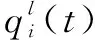
1.2 GRU神經網絡

傳統RNN方法在處理長序列數據時，隨著數據量的不斷增加，因為網絡結構的原因，會因數據長期依賴帶來梯度消失和梯度爆炸等問題，影響最終的預測效果。為解決這些問題，GRU和LSTM神經網絡隨之而生。這兩者都通過引入一組儲存單元，使得神經網絡可以自主學習，保存重要歷史信息，及時更新儲單元[13]。兩者不同的是，GRU的網絡結構將LSTM網絡的輸入門和遺忘門合二為一成為更新門。GRU的具體結構如圖1所示。

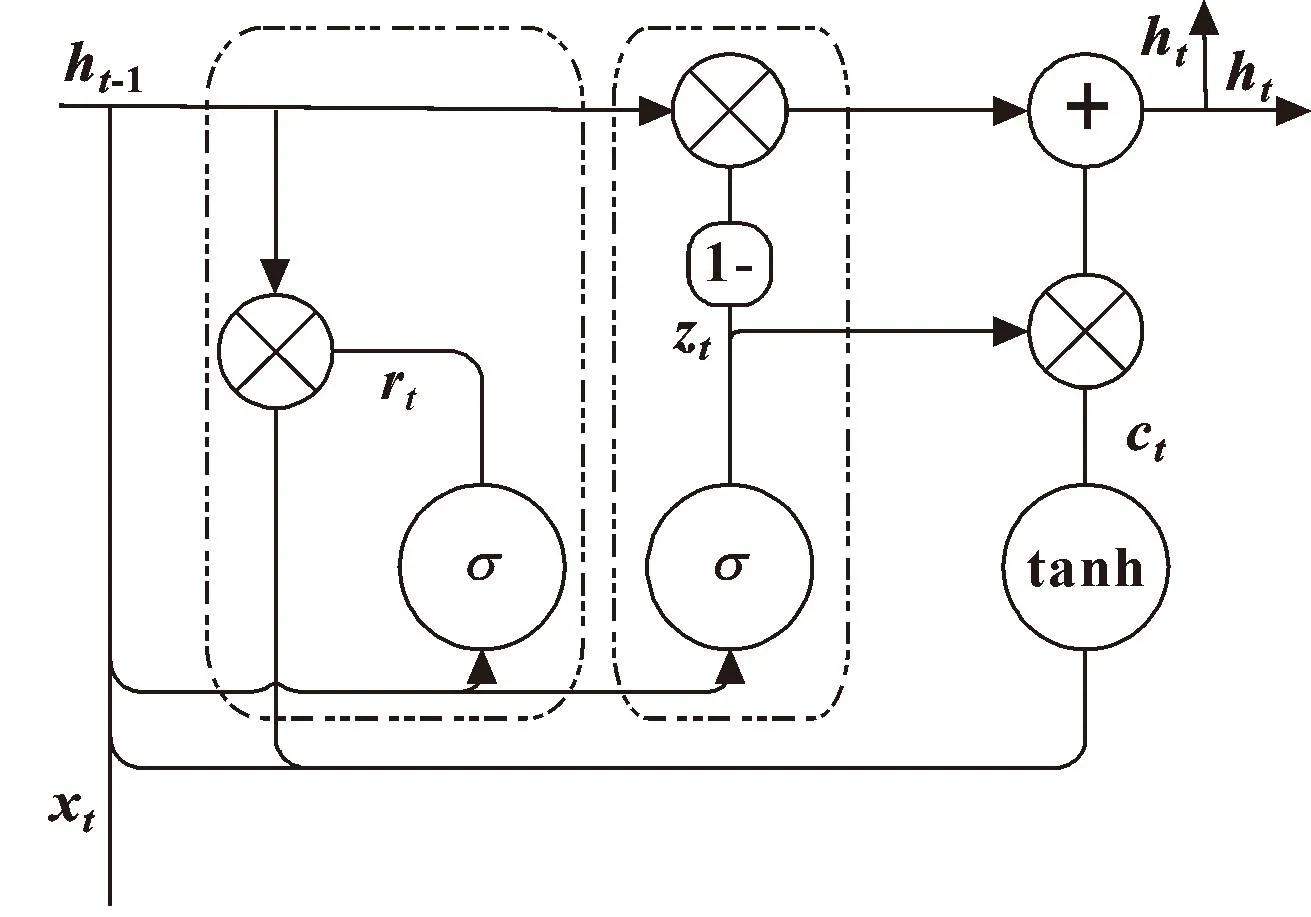
圖1 GRU網絡結構Fig.1 GRU network structure

圖中，zt為更新門，rt為重置門。其中更新門的作用是調整前一時刻狀態ht-1對當前狀態ht的影響量。前一狀態對當前狀態的影響越大，更新門的數據值越高，數據傳入的信息越多。其表達式如式(3)所示：

zt=σ(wxz+xt+whzht-1+bz)

(3)

重置門的作用是控制前一時刻的狀態ht-1對候選狀態ct的影響量。前一狀態對候選狀態的影響越小，重置門的數據值越低，數據傳入的信息越少。

重置門的表達式和更新門表達式相同，只是線性變換的參數和偏置有所改變，計算方法見式(4)：

rt=σ(wxrxt+whrht-1+br)

(4)

最后，可得候選狀態ct和輸出ht為

ct=tanh(wxcxt+whc(rt?ht-1)+bc)

(5)

ht=(1-zt)?ht-1+zt?ct

(6)

式中：xt為輸入序列；ht-1為上一時刻隱藏狀態；ht為當前隱藏狀態；wxz和whz是更新門的權重矩陣；wxr和whr是重置門的權重矩陣；wxc和whc是候選狀態的權重矩陣；bz、br、bc表示相應的偏置。圖中的?表示逐元素相乘，tanh表示tanh函數作為候選狀，σ表示Sigmoid函數，其表達式分別如公式(7)和公式(8)所示。

tanh(t)=(et-e-t)/(et+e-t)

(7)

σ(t)=1/(1+e-t)

(8)

設置Sigmoid函數作為更新門和重置門的激活函數，輸出值固定在0～1之間，以此達到保留或忘記信息的效果。

1.3 信息融合

由于采集到的振動信號和聲發射信號中量綱不統一，需要對特征信息進行信息融合。根據融合方式的不同，信息融合技術可分為決策層融合、數據層融合和特征層融合。決策層融合會對采集的數據進行壓縮處理，勢必導致信息的大量丟失，不適合處理軸承壽命數據。由于振動傳感器和聲發射傳感器探測技術不同，因此不適合直接將數據合并的數據層融合。特征層融合是先分別提取不同傳感器的特征值，之后通過歸一化處理消除不同傳感器的差別，能夠有效保留軸承退化信息。此次試驗選用特征層融合[15]，其融合方式如圖2所示。

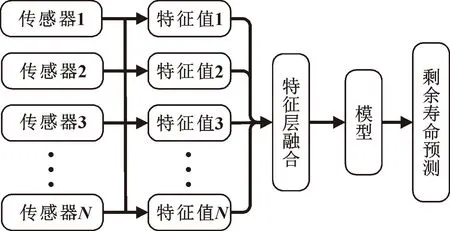
圖2 融合方式Fig.2 Fusion method

選擇歸一化進行特征層融合。一維卷積采集到的信號特征屬于離散型數據變量，適合選用線性歸一化方法。線性函數常用的歸一化方式如公式(9)所示：

(9)

其中：x為經過特征提取后的離散數據；xmin為處理后數據的最小值；xmax為處理后輸入數據的最大值；y為最終的輸出值。

1.4 軸承壽命預測流程

圖3所示為牽引電機軸承壽命預測流程。具體為以下步驟：

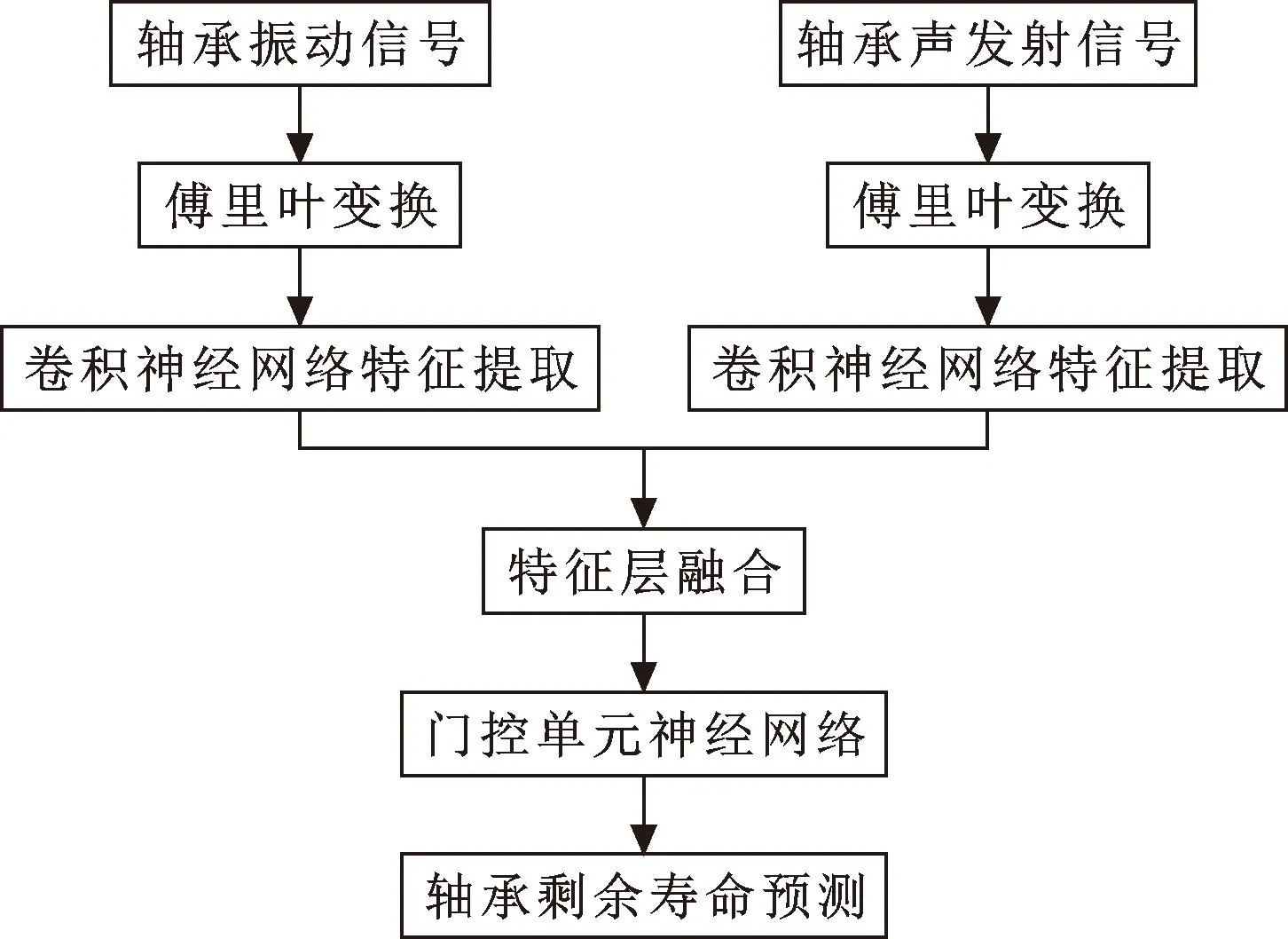
圖3 軸承壽命預測流程Fig.3 Flow of bearing life prediction

(1)信號采集。使用振動傳感器和聲發射傳感器分別采集軸承的振動信號和聲發射信號。

(2)特征提取。對采集到的軸承振動信號和聲發射信號進行傅里葉變換(Fast Fourier Transform，FTT)，使用卷積神經網絡自動提取出包含退化信息的特征數據。

(3)歸一化處理。為減少不同傳感器采集數據的物理影響，需要對提取出的振動信號和聲發射信號的特征進行歸一化處理。

(4)剩余壽命預測。以歸一化后的特征參數作為神經網絡的輸入、軸承的剩余壽命作為標簽對CNN-GRU模型就行訓練。

2 試驗驗證

2.1 試驗設計及平臺

文中使用的地鐵牽引電機試驗軸承型號為NU216，結構參數如表1所示。

表1 軸承結構尺寸Tab.1 Bearing structure dimensions

為了減少試驗周期，同時模擬軸承實際運行中可能產生的早期缺陷，使用大族YLP-MDF-152型三維激光打標機在滾動體上進行缺陷預制，預制的點蝕直徑為20 μm，裂紋寬度為15 μm，在此基礎上進行剩余壽命試驗。

試驗按照GB/T 24607-2009《滾動軸承 壽命與可靠性試驗及評定》標準進行[14]，詳見表2。共采集2 000組包含軸承衰退信息的信號。

軸承退化信息采集系統由軸承試驗臺、試驗軸承、傳感器采集模塊液壓加載模塊和計算機組成，如圖4所示。

圖4 軸承試驗臺Fig.4 Bearing test bench

2.2 軸承壽命預測流程

首先對采集到的振動數據和聲發射數據進行傅里葉變換(FTT)，之后使用一維卷積神經網絡對特征進行深度提取。

對提取出的特征信息歸一化處理后劃分訓練集測試集。對模型進行訓練前要對軸承數據集樣本進行壽命標簽設置。引入健康度指標(HI)作為標簽，其計算公式如式(10)所示：

(10)

式中：T為全部的數據集數量；t為當前的數據集序號；δHI的取值為0～1。數據集序號按照時間序列排序。0點代表軸承完全失效時刻，1點代表軸承退化起始點時刻。最后，雙通道數據的CNN-LSTM和單通道數據的CNN-GRU網絡進行對比，以驗證模型的有效性。

文中設計的網絡模型由特征提取層和分類層組成，具體設計為卷積-卷積-池化-卷積-卷積-池化-卷積-卷積-池化-卷積-卷積-池化-全連接-GRU分類器的結構模型。其中，池化層采用最大池化方式。模型參數如表3所示。

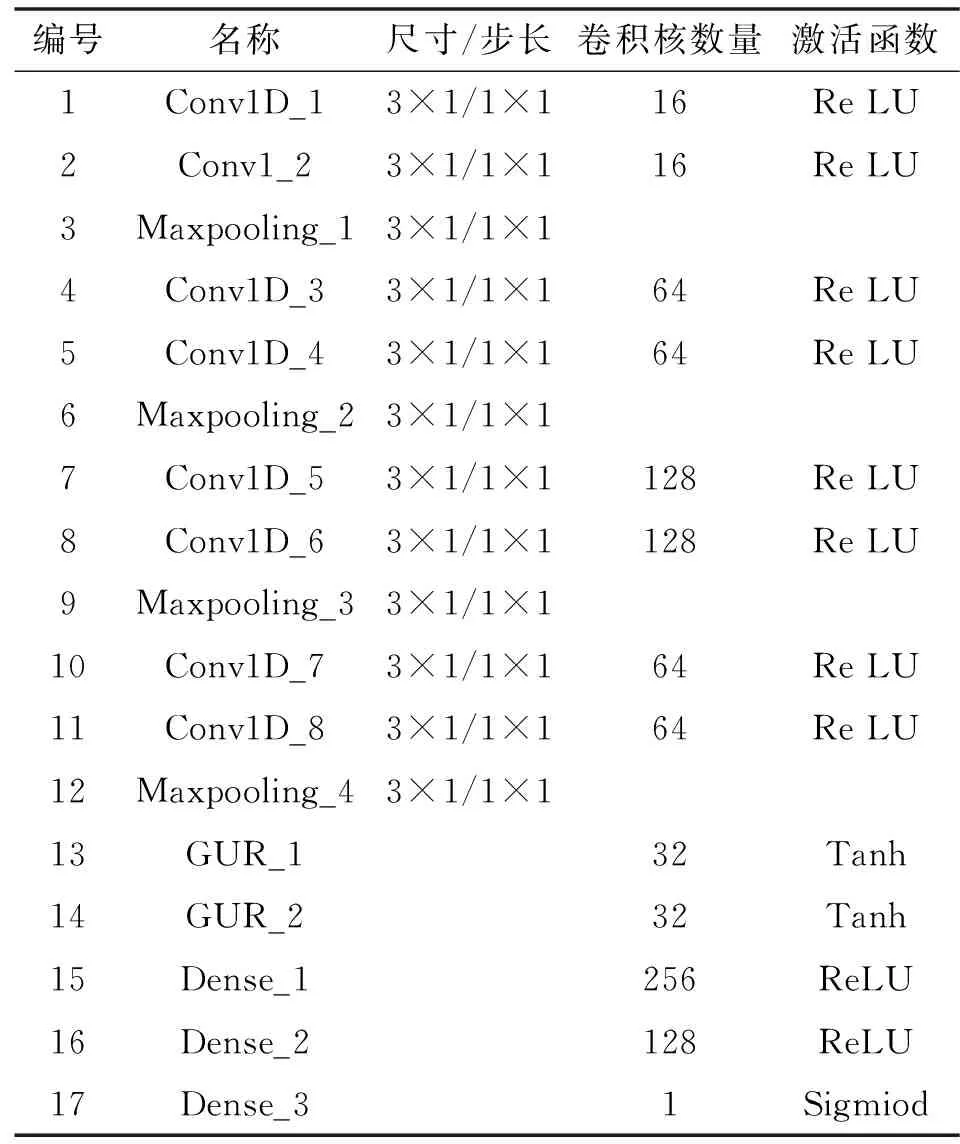
表3 模型結構與參數配置Tab.3 Model structure and parameter configuration

將歸一化后的特征數據輸入GRU網絡進行訓練，同時將均方誤差函數作為損失函數，并采用Adam優化器對網絡權值進行更新。將測試集的退化特征向量輸入到訓練好的GRU模型當中，輸出得到測試集軸承的剩余壽命。

由圖5可以看出：當迭代次數達到30次左右時，模型的損失函數已經穩定。圖6所示為預測效果。可以看出：經過雙通道數據訓練的CNN-GRU模型的擬合效果良好。

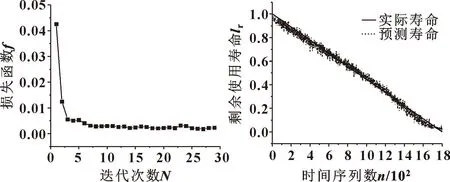
圖5 損失函數曲線 圖6 雙通道CNN-GRUFig.5 Curve of loss function Fig.6 Dual channel CNN-GRU

為了達到對比效果，單振動信號輸入的CNN-GRU模型和雙通道輸入的CNN-LSTM模型使用同一數據進行壽命預測。效果如圖7、8所示。為了進一步說明模型的預測效果，用均方根誤差(Root Mean Square Error，RMSE)為指標進行評估，均方根計算公式如式(11)所示。計算結果見表4。

表4 預測誤差Tab.4 Prediction errors

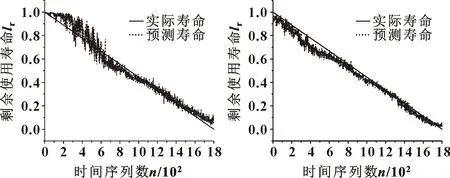
圖7 單通道CNN-GRU 圖8 雙通道CNN-LSTMFig.7 Single channel CNN-GRU Fig.8 Dual channel CNN-LSTM

(11)

式中：m為數據數量；y(i)為模型輸出的預測值；x(i)為采集到的真實值。

由圖7、8和表4可知：(1)雙通道CNN-GRU模型相較于單通道的CNN-GRU模型預測誤差更低，說明采用信息融合技術的雙通道預測模型能夠有效提高預測精度。(2)雙通道CNN-GRU模型相較于雙通道的CNN-LSTM模型預測誤差更低，說明最后的預測算法選擇結構更簡便的GRU模型比LSTM模型效果更好。

3 結束語

為解決單一傳感器信號易受干擾且能提取的退化信息有限，導致軸承剩余壽命預測精度低的問題，以地鐵牽引電機軸承為例進行一定時長的非全壽命試驗，并提出基于CNN-GRU的剩余壽命預測方法。

搭建了地鐵牽引電機軸承試驗臺，對軸承進行了試驗，采集的振動信號和聲發射信號經過傅里葉變換后得到頻域信號，通過卷積神經網絡學習其不同頻帶的特征，歸一化后再通過門控單元神經網絡學習序列數據潛在的時間關系，對其深層特征進行有效挖掘。

最后通過試驗驗證了文中所提方法的可行性，并與單通道CNN-GRU和雙通道CNN-LSTM方法進行對比，通過定量分析說明了文中方法具有更小的預測誤差，能夠為地鐵牽引電機軸承的壽命預測提供一種新思路。